考虑转向延误及尾气排放的禁左双层规划模型

常玉林，朱俊炜，张 鹏，孙 超

（1.江苏大学 汽车与交通工程学院，江苏 镇江 212013；2.东南大学 城市智能交通江苏省重点实验室，南京 211189）

交叉口是拥堵的关键节点，对于难以改扩建的交叉口，通过禁左的限制手段以提高交叉口的通行能力，减少车辆排队积压、反复启停导致的局部高排放是最直接有效的方法。但禁左的弊端就是产生绕行，因此国内外已有的禁左研究有相当一部分是关于禁左绕行方式的选择［1］、远引掉头位置的选择［2-4］等定性分析结果。

禁左看似是牺牲了交叉口左转车辆的利益但是其减少了交叉口冲突、为直行车辆留出来车道及有效绿灯时间，这对于整个区域路网来说是有利的，因此禁左问题不能简单地对单一交叉口节点进行分析而需要立足于网络交叉口节点［5］。基于此，关于禁左问题的研究逐渐由单一交叉口禁左推进到交通网络交叉口群之间的禁左决策目标规划上来，龙科军等［6］较早地通过增设虚拟边的方法建立了禁左双层规划模型，将转向虚拟边与真实路段相同处理，借助遗传算法对模型求解，得到了部分网络交叉口的最优组合策略。樊慧敏［7］在此基础上，考虑了禁左备选交叉口的选择，并选取了实际区域交通路网进行计算验证了现有禁左模型的有效性。李琦等［8］在增设虚拟路段的同时重点挖掘禁左对阻抗函数的影响。

现有禁左模型解决了区域交叉口的转弯禁限设计问题TRDP（turning restriction design problem），但也存在一些不足及假设条件不切合道路交通实际等问题。如现有模型多假设某一进口禁左则其对向进口也禁左，且仅考虑两相位控制，这与交叉口多为四相位的实际不符；又如增设虚拟路段的方法扩大了路网节点个数不利于求解，同时将计算真实路段阻抗的BPR函数用于计算转向虚拟边阻抗并不能体现转向延误的真实情况；而且均忽略了对禁左进口道个数的有效限制，禁左越多易使对该区域不熟悉的驾驶员产生疑惑从而带来安全隐患。

本研究基于绿色交通理念首次将尾气排放加入禁左双层规划模型，使上层目标为系统总阻抗和总排放最优。建模时将邻接路段法替代了用虚拟路段表示转向的传统方法，并将转向延误单独计算更贴合道路交通实际。本文可实现不定交叉口不定进口的禁左方式，并通过设计四相位的改进方法允许单进口禁左方案。模型计算使用遗传算法并用Matlab求解区域交叉口禁左最优组合。

1 建模准备

1.1 传统禁左模型的改进

1.1.1 单进口禁左的信号相位设计

传统禁左规划模型对于禁左假设条件的要求较为严格，均假设某一进口禁左则其对向进口也禁左［6-8］；甚至在考虑排放的禁左规划模型中将假设条件设为：没有独立的左转信号灯［9］，即仅考虑简单的两相位信号控制。但在实际道路网络中转向车流分布并不总是对称的，当对向左转流量较大时不能随意对其禁左，因此传统“一禁全禁”的模式是不符合实际的。

四相位信号控制下的单进口禁左控制作为本文的创新之一其实用价值更高，且灵活多变的特点给禁左组合带来了更多的选择。针对本向禁左而对向不禁左模式，考虑既要保留左转相位又不能造成左转绿灯时间的浪费，因此设计不禁左向直行和左转的叠加相位方案。以南进口禁左北进口不禁左为例，改进后单进口禁左信号相位设置如图1所示。

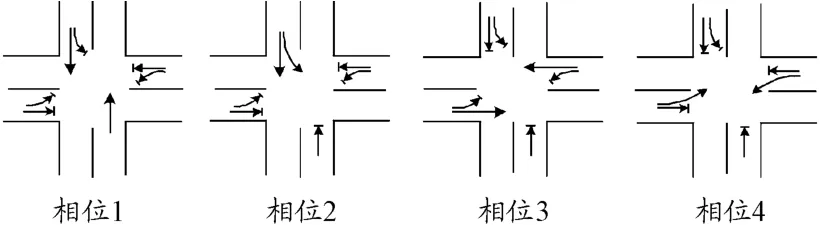
图1 单进口禁左信号相位设计示意图

南进口禁左后，直行车流借用原左转车道通行提高了南进口直行通行能力；北进口直行车流通行时间增加同样提高了北进口直行通行能力。此情形尤其适用于南进口左转流量不大，北进口直行和左转流量均较大的交通流状态。

1.1.2 动态禁左

由于大部分交叉口一天之内的流量都是动态变化的，尤其是早晚高峰往往呈现潮汐特征，因此区域交叉口网络中禁左组合方案不应该是固定不变的。例如图1所示南进口禁左方案就更适用于某一时段北进口直行和左转流量均大于南进口的情况，而当流量发生变化时，通过禁左模型计算得到的禁左进口道及交叉口也会发生相应的变化。

相反，在传统禁左规划“一禁全禁”的假设中，并不能很好地反映交叉口2个方向流量变化带来的禁左组合变化效果。而本研究真正能做到不定交叉口不定进口道的区域交叉口禁左控制效果。

但是一天内甚至较短的一段天数内禁左动态变化的次数及禁左交叉口的个数不宜过多，因为这对于驾驶者的驾驶习惯是一种挑战，存在相应的安全隐患。因此这里提出的动态禁左并不是对流量变化的时时反映，与动态交通分配无关。

1.1.3 转向车流的邻接路段表示方法

传统禁左规划及考虑排放的禁左对于转向车流的处理，均采用增设虚拟路段的方法：将原有的一个交叉口节点变为8个，同时生成不同流向的12条链［6］。这样处理容易将转向与真实路段混淆，同时也人为地增加了工作量。对于局部路网有一定的可操作性但随着路网规模和交叉口个数的增多其适用性大幅降低。

本研究不同于增设虚拟路段的方法，采用邻接路段的方法表示转向车流［10］，彻底将转向与真实路段区分开来，有利于后续阻抗及尾气排放的独立计算。即对任意转向a→b，其在连接OD对ω的路径k上当且仅当路段a和路段b同样在该路径上，此时随着OD对ω之间路径流量的确定，该路径上各转向流量也随之确定。

1.1.4 转向延误的确定

城市路网中转向延误是不可忽略的且需分流向计算，这是由于城市路网具有交叉口多而密的特点决定的。当交叉口拥堵时转向延误有超过路段延误的可能。

在对转向延误进行计算时，一般用Dij表示来自前一节点i的车辆在下一交叉口节点j的延误，但每一辆车从节点i经过节点j后其左、直、右不同流向的选择会带来3个不同的转向延误，因此不能简单地用同一个Dij来刻画这些延误。

对于这个问题，现有禁左规划多忽略转向延误的计算，只借用BPR函数计算路段阻抗作为路网的总阻抗［11］。而考虑排放的禁左现有研究，虽然考虑了转向延误的计算但仅考虑了单一禁左组合下的转向延误，准确性和实用性有待提高。

本节中单进口禁左控制正好能解决单一禁左组合的问题。因此本研究基于平均信控延误模型（HCM，2000）［12］：

将部分参数定值化并以进口“一左一直一右”三车道为例计算得到不同禁左模式下的转向车流平均阻抗tab取值如表1所示（假设右转车流阻抗为0，以南进口为例）。

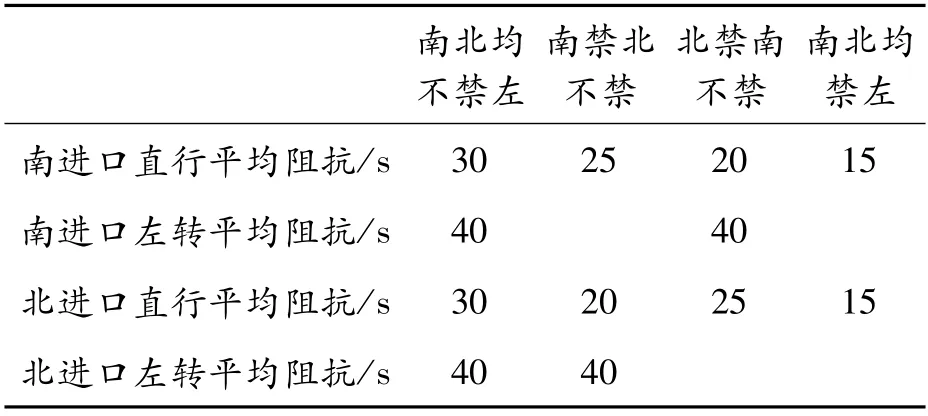
表1 4种禁左组合下南北进口各转向平均阻抗建议值

当某一进口禁左时，本向直行借用左转车道从而使车道饱和度降低转向延误降低；对向直行在原有相位的基础上跟随其左转车流继续通行，绿信比增加车道饱和度降低转向延误降低。当本向和对向均禁左时，两向直行均借用左转车道且左转相位取消加到直行相位上，车道饱和度降低、绿信比增加转向延误显著降低。

1.2 尾气排放函数

现有排放+禁左的研究中，假设排放只取决于流量且将转向用虚拟路段表示，从而在计算虚拟路段与真实路段时用同一个排放公式，这显然不能很好地反映路网真实的排放状态。

本研究将真实路段与转向区分开，分别计算车辆匀速及怠速行驶下的尾气排放量，同时考虑排放量不仅与流量有关还与匀速及怠速下的行驶时间有关，这也是本研究最主要的不同与改进。

对于尾气排放的评价一般是用3种主要污染物CO、HC和NOx的总量来表示。但在交通优化问题中一般仅以污染物CO为例进行计算，主要原因有以下两点：①不同污染物的排放因子在表达形式上相似，它们在交通UE分配中的影响也是一致的［13］；②研究时一般将CO作为主要危害物来进行评价，因为其所占的比例最大。

1.2.1 路段匀速排放

路段匀速工况的排放主要与交通量、匀速排放因子及路段长度有关，其表达式如下［14］：

其中：

式中：G1为路段匀速排放总量；A为路段集合，a∈A为任意路段；xa为路段a的交通流量；EPCUa 为CO路段匀速排放因子，由TRANSYT-7F平均速度模型确定；La为路段a的长度；va为路段a上速度的平均值；B、C、D均为路段匀速排放因子主要参数，分别取：B=11.142 72，C=0.047 772，D=3 280.8［14］。

1.2.2 交叉口怠速排放

车辆驶经交叉口附近时其怠速行驶的主要原因是受交通信号灯的延误影响，因此可令车辆在交叉口处的怠速时间等于其平均信控延误时间。交叉口怠速工况的排放主要与转向流量、怠速排放因子和怠速时间确定，其表达式如下［14］：

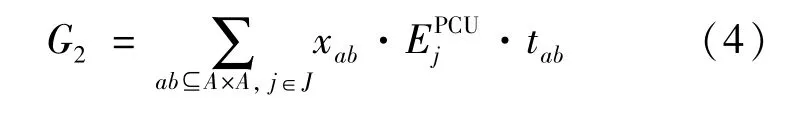
其中：

式中：G2为交叉口怠速排放总量；J为交通网络中所有交叉口的集合，j∈J为其中任意交叉口；xab为转向a→b的交通流量；EPCUj 为CO怠速排放因子；tab为转向ab的阻抗，取定值见表1。

2 禁左双层规划模型

2.1 上层模型

双层规划模型因为其特有的上下层互相约束的结构特点，逐渐成为了解决复杂交通决策问题的重要建模手段，既表达了道路使用者的个体诉求又满足了道路管理者的系统最优目标。

上层模型便是道路管理者对路网性能的全局把控，本文拟通过设置合理的禁左组合来最小化区域交叉口的行程时间和尾气排放总量。并为了更好地体现转向延误对禁左模型的影响，将路段流量与转向流量区分开，分别计算其阻抗与尾气排放量。故改进后的禁左上层模型如下。

①上层目标函数表达式为（路网总阻抗+总排放加权和最小）：

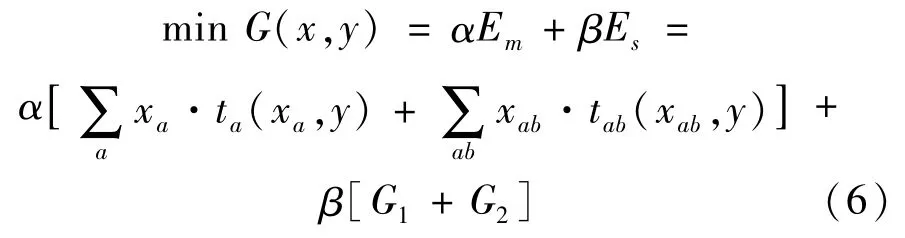
②上层约束条件为：

路段约束

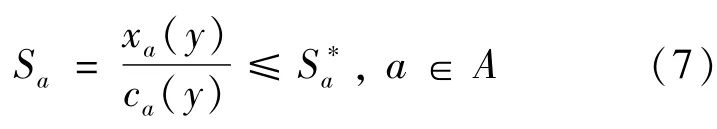
转向约束

式中：α、β表示权重系数，可调整总行程时间与总排放的占比，α+β=1；Em表示总行程时间；Es为尾气排放总量；y为禁左0-1变量，1和0分别表示该进口禁左／不禁左；ta为路段a上的阻抗，该阻抗采用美国道路局BPR函数进行计算［15］；Sa、Sab均表示为饱和度的建议值；S*a、S*ab均为饱和度的最大值；xa，xab均为y的隐函数。

禁左开关变量y为上层决策变量，其取值将直接影响下层决策变量的可行域。而上层中的路段流量xa和转向流量xab则为下层决策变量，其由Frank-Wolfe算法［16-18］计算求得交通配流结果，同时也会影响上层决策变量的可行解。因此xa和xab均是以禁左决策变量y为自变量的函数，即xa（y）、xab（y）。其中路段流量由交通分配得到，转向流量随路径流量确定。同时为避免过多禁左对于行车安全的影响，禁左决策在实例路网的求解中不应多于5个。

2.2 下层模型

上层禁左决策的改变会导致路段及交叉口阻抗的变化，而下层模型中的道路使用者总是希望寻求最短路，因此随着禁左决策的改变下层会不断形成新的平衡。新平衡下的流量可根据Wardrop第一原则建立用户平衡分配模型（UE）求得［19］，改进后的禁左下层模型表达如下。

③下层目标函数表达式为：

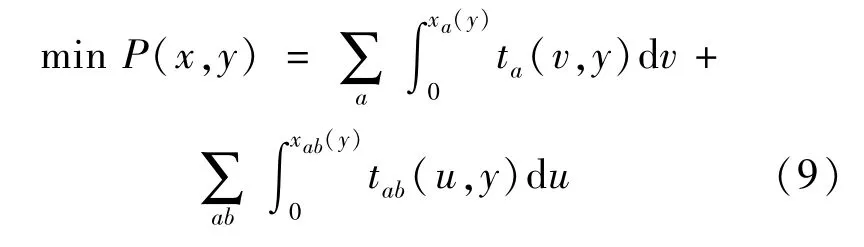
④下层约束条件为：

路径流量和

流量非负

路段流量

转向流量

转向车流的表达

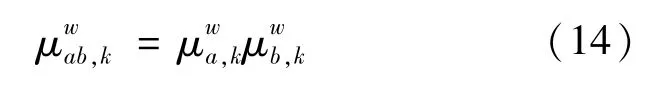
式中：W表示交通网络中起讫点对的集合，w∈W；qw为起讫点对w的交通需求；kw为起讫点对w中所有可能路径的集合；fwk为OD对上第k条路径的流量；μwa，k为0～1变量，μwa，k=1表示路段a在OD对w上，反之μwa，k=0；μwab，k为0～1变量，=1表示转向a→b在OD对w上，反之μwab，k=0；

其中式（13）为对现有禁左双层规划模型下层约束条件的改进，其依据为：转向a→b在连接OD对w的路径k上，当且仅当路段a和b同样在该路径上。

3 模型求解算法

双层规划模型属于有约束的非线性规划难题，对这类问题的求解多用遗传算法或粒子群算法。但本文基于禁左的双层模型为非线性0～1变量整数规划模型其含有大量的二进制变量，因此遗传算法更为适用。同时下层规划模型为典型的UE问题，而对于UE问题的求解多用交通规划中成熟的Frank-Wolfe算法，从而将求解出的路段及转向流量代入上层模型，这是嵌套在遗传算法中的关键一步。

改进后的禁左双层规划模型具体求解步骤如下：

1）确定禁左变量初始种群

确定研究区域目标交叉口个数，每个交叉口包含4条左转进口道，每一个左转又对应一个禁左开关变量Y，共m个。

按一定的顺序排列并编码，用计算机随机得到m个01二进制数，并将其设为一条染色体，其中1表示禁左0表示不禁左。30～60条染色体作为一个初代种群［20］。

2）计算适应度大小

将每条染色体代入下层并通过预设的Frank-Wolfe算法求得各路段流量，将结果回代到上层得到每个种群中不同染色体对应的最优解G。设适应度函数表示为F（yi）=1-G／sum G，可知最优解与适应度成反比。

3）优质目标种群的选择

根据染色体适应度计算结果，保留较大的继续迭代，并将这些留下来的染色体筛选形成新的种群，从而不断接近最优目标。

4）交叉

将优质种群中的染色体随机配对，按照Pc的概率随机选定其中一个点位，将两者在该选定点位上的基因互换。

5）变异

变异与交叉的方法类似，按照Pm的概率在染色体上随机选择某一点位后，将该点位上的二进制数相反，即1变0，0变1。

6）终止条件

4 实例计算及应用

为了验证改进后的禁左双层规划模型的有效性及准确性，需设计区域交叉口路网并进行仿真实验及计算。

本文采用Dial区域交叉口路网，结构如图2所示。共9个交叉口节点，其中1、3、7和9又兼为网络中OD对的起点和终点，其交通分布见表2。每2个节点之间均为双向路段共24条，每条路段的通行能力都是一定的。网络共有4对OD点对、44个转向，其中左转16个，从节点1到16按照由北到南由西到东的顺序将16个左转依次编号。

路段阻抗函数关键参数取值见表3，其中考虑到城市交叉口间距多为1 000～1 500 m，因此零流阻抗t0a取70～95 s的随机数；次干路通行能力取1 400 veh/h、主干路取1 600 veh/h［10］；转向延误取值见表1。

设计该仿真实验路网的主要依据有以下3点：

1）由于禁左规划模型均是给定OD需求并通过交通分配得到各路段流量，因此实际路网获取的交通量数据并不能直接使用，只能设计具有真实路网相关特性的虚拟路网来进行仿真实验。

2）考虑禁左控制须有相邻替代道路且绕行距离不宜过长，因此棋盘网格状交叉口群最适合［7］。

3）现有禁左仿真实验中虽然设计的路网较大但仅考虑单一OD点对间的单一流向，这不仅限制了路网中左转的个数也限制了禁左组合的多样性。因此本仿真实验设计路网中包含两对OD且均为双向需求。

图2 区域交叉口路网结构示意图

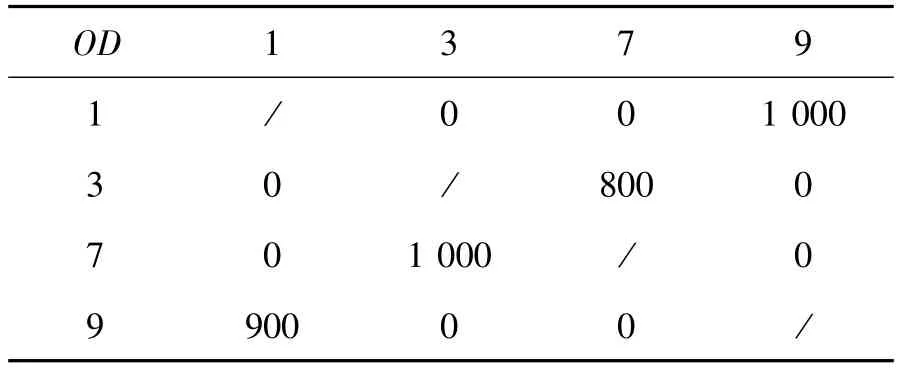
表2 起终点OD交通分布

根据式（1）～（13）建立该研究区域禁左双层规划模型，并代入上述参数，其中权重系数α=β=0.5即认为路网总阻抗与总排放同样重要，va取60 km/h。种群数取30，Pc=0.60，Pm=0.003［20］。

用Matlab迭代50次后得到最终优化结果：y=［1000010000001001］，即节点1东左、节点4东左、节点7北左及节点9西左实施禁左交通管理。禁左前后各路段流量及饱和度见表4，均满足饱和度要求且路网总阻抗和总排放量的加权和G由不禁左时（即y全取0）的1.584 5×106s降低为1.510 3×106s；其中交叉口怠速排放总量E2下降最为明显由不禁左时的8.800 7×104g降低为7.817 6×104g，禁左组合控制效果达到了11.2%，该结果证明本文考虑转向延误及尾气排放的改进禁左模型具有较好的先进性。

表3 路段阻抗函数关键参数取值

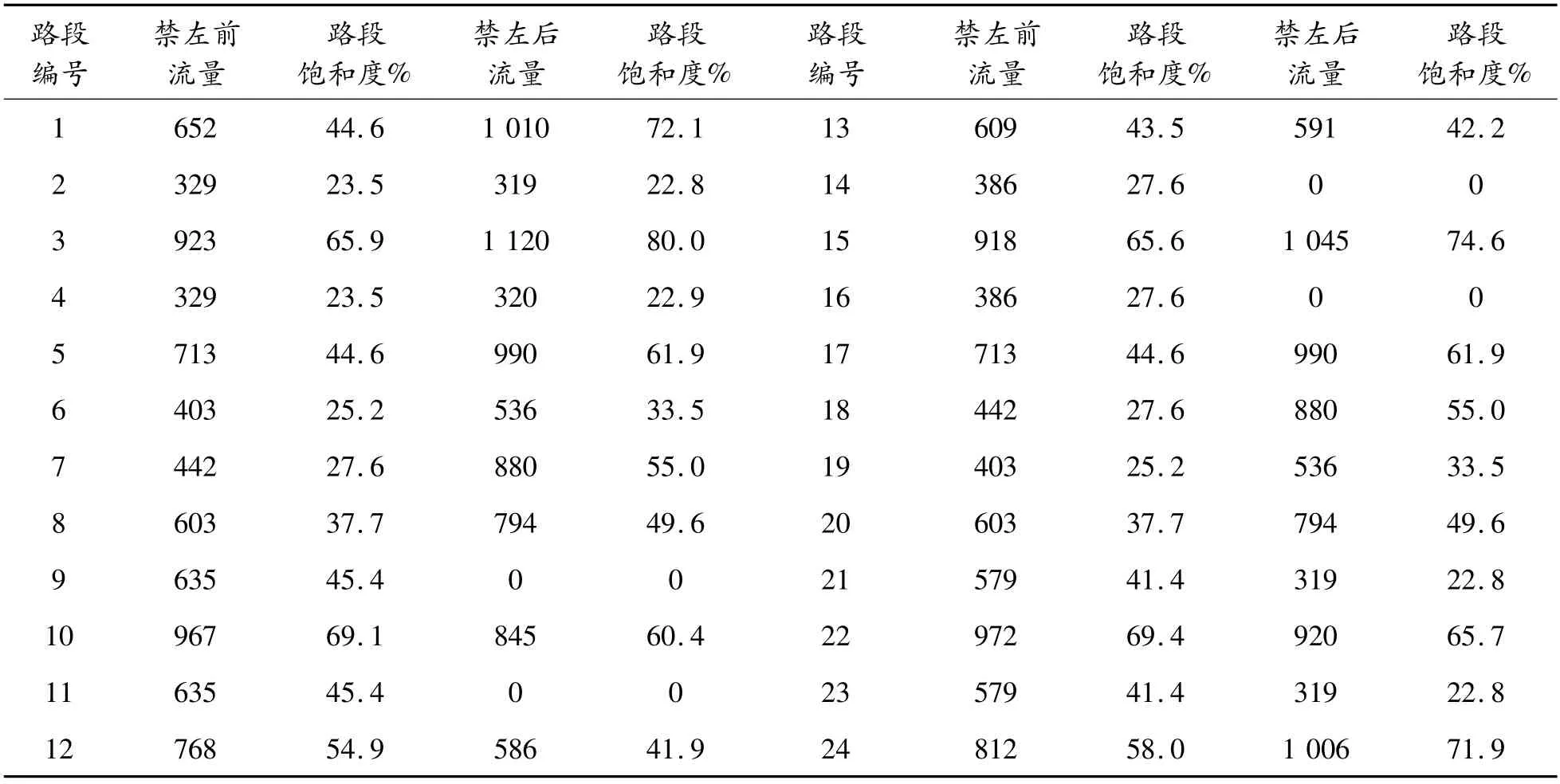
表4 禁左前后区域各路段流量及饱和度

5 结论

禁左交通规划是区域交通组织与交通管理措施有机结合的体现。禁左控制虽然会带来局部的绕行而引起局部排放量的增加，但能有效增加直行通行能力，从而缓解直行车流造成的拥堵及排放，合理选择禁左交叉口可以改善区域交通行车条件。

本文基于对禁左模型的改进建立了新的禁左双层规划模型，构建了对区域交叉口禁左组合的综合评价方法，为拥堵区域禁左进口道的选取提供了一种科学而又可靠的计算手段。通过对实例路网的求解计算，证明了在区域交叉口合理设置禁左组合可以有效减少行程时间和尾气排放，尤其对于交叉口怠速排放的改善效果显著。

下一步的研究主要分为两部分，一是应加强对求解精度的控制与判别，二是应选取城市真实交叉口路网状况进行进一步的求解与仿真，这对于改进的禁左规划模型和参数的修正具有更为重要的实际意义。