基于极小值原理的AM T车辆起步最优协调控制策略

2021-03-22赵克刚宁武林

重庆理工大学学报(自然科学) 2021年2期

赵克刚，宁武林，叶杰

（华南理工大学汽车零部件技术国家地方联合工程实验室，广州 510640）

近年来，通过对车辆起步过程中发动机与离合器间的协调控制策略的优化以改善起步动力性、经济性和乘坐舒适性，并延长传动系统关键零部件的使用寿命等，逐渐成为机械传动领域的研究热点［1］。

孙冬野等［2］针对机械式自动变速器（automatic mechanical transmission，简称AMT）车辆起步过程，提出了发动机的局部恒转速控制策略，反映了驾驶员的起步意图并有效地抑制了起步过程中发动机的转速抖动。在孙冬野等研究［2］的基础上，部分学者将模糊控制策略［3］、滑模变结构控制策略［4］及神经网络控制策略［5］等应用于AMT、DCT（dual-clutch transmission）车辆的起步控制过程中，以获得良好的车辆起步性能。

部分专家学者提出将最优控制理论应用于车辆起步控制策略的优化中。秦大同等［6］通过选取不同的控制、状态变量及二次型优化目标的形式，基于线性二次型最优控制算法（linear quadratic gaussian，简称LQG）确定了AMT或DCT起步过程中离合器的最优接合规律。赵治国等［7］针对DCT车辆的起步过程，在发动机侧采用局部恒转速控制策略，在离合器从动侧基于极小值原理获得离合器的最优接合规律。高炳钊等［8］基于模型预测控制算法在线优化发动机和离合器的转矩及转速轨迹曲线，以平衡起步过程的滑摩功和冲击度等性能指标。上述文献［6-8］均采用数值求解方法获得AMT或DCT车辆起步过程的最优控制规律，但数值求解计算耗时较多，不便于将其直接移植应用于车辆起步的实时控制器中。

针对AMT车辆起步的动力学过程，以滑摩功、冲击度和控制能量等的加权和作为优化目标，在满足驾驶员起步意图的终端约束条件下，构建了发动机与离合器间的最优协调控制问题。并基于极小值原理将其转化为等价的微分方程组的边值问题，经数学推理演算可得到最优控制和状态变量轨迹曲线的解析表达式。分析和比较基于解析求解方法和数值求解方法所得到的最优控制、状态变量的轨迹曲线，验证了解析求解方法更适用于实时控制系统中。基于快速原型控制器Rapid-ECU-UIM和Simulink/RTW 编译环境，搭建了车辆起步控制的硬件在环仿真试验平台，提出了基于解析求解方法的车辆起步最优协调控制策略，开展了不同加权系数组合和不同节气门开度条件下的硬件在环仿真试验以验证其有效性和实时性。

1 AMT车辆起步动力学过程分析

1.1 AM T车辆起步过程分析

参照文献［9］，AMT车辆起步过程可分为准备期、半接合点前的滑摩期Ⅰ、半接合点后的滑摩期Ⅱ和转速同步期4个阶段。

1）准备期：离合器逐渐接合以消除其主、从动部分间的间隙直至开始接触的过程；

2）半接合点前的滑摩期Ⅰ：随着离合器压力逐渐增大，其传递的摩擦转矩也逐渐增大，但传递至驱动轮的驱动力矩仍小于车辆静止阻力矩，车辆保持静止不动；

3）半接合点后的滑摩期Ⅱ：随着离合器传递的摩擦转矩逐渐增大并克服车辆静止阻力矩，车辆开始移动，离合器从动部分的转速也逐渐升高至与主动部分同步；

4）转速同步期：当离合器主、从动部分转速完全同步之后，离合器由动摩擦状态切换至静摩擦状态，且离合器压力继续增加直至完全接合。

在准备期和滑摩期Ⅰ这2个阶段中，离合器的接合快慢并不会引起车辆的纵向冲击，为满足快速起步的要求，应在发动机不熄火的前提下尽快地接合离合器。在滑摩期Ⅱ，离合器接合速度较大，会引起发动机转速波动较大且造成较大的车辆冲击，影响起步平顺性；离合器接合速度较慢，则会造成起步缓慢且延长离合器滑摩时间，增大离合器的滑摩功从而降低离合器使用寿命。在转速同步期，离合器主、从动部分转速同步且离合器完全接合，故并不会因离合器的滑摩产生滑摩功，则可在满足冲击度的约束条件下尽快地将车速提升至目标车速，完成整个起步过程。

基于AMT起步过程4个阶段的机理分析可知，半接合点后的滑摩期Ⅱ中发动机与离合器间的协调控制是影响车辆动力性、经济性等起步品质的关键。

1.2 AMT车辆起步动力学模型

为便于AMT车辆起步控制策略的研究，采用集中参数建模，简化后所建立的AMT起步动力学模型如图1所示［10］。

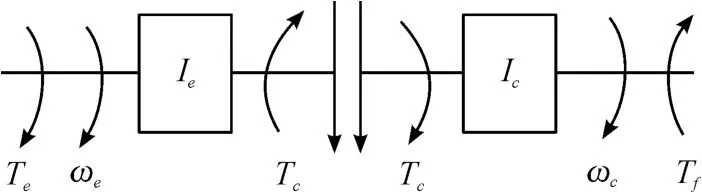
图1 AMT车辆起步动力学模型示意图

图1中符号定义如下：Ie为发动机、离合器主动部分等部件等效至发动机端的当量转动惯量；Ic为离合器从动部分、变速器、主减速器、车轮及车身等部件等效至离合器从动端的当量转动惯量；Te为发动机输出转矩；Tc为离合器传递转矩；Tf为等效至离合器从动端的车辆行驶阻力矩；ωe为发动机端转速；ωc为离合器从动端转速。

AMT车辆起步过程半接合点后的滑摩期Ⅱ中传动系统的动力学方程为：

离合器的传递转矩Tc可表示为［11］：

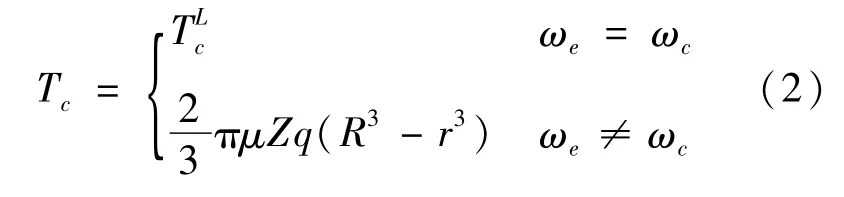
式中：μ为离合器摩擦片间的摩擦系数；z为摩擦片个数；R和r为摩擦片的外径和内径；q为执行机构作用于摩擦片的单位面积压力；TLc为离合器完全接合时所传递的惯性力矩。

等效至离合器从动端的车辆行驶阻力矩为：

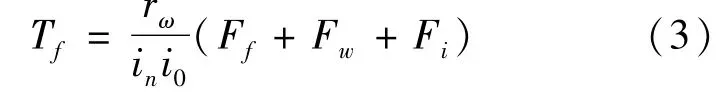
其中，滚动阻力、空气阻力和坡度阻力为：

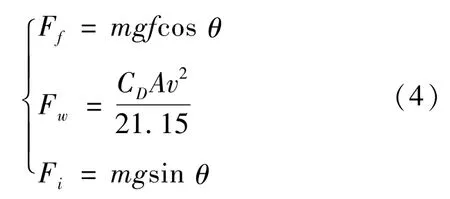
式中：rw为车轮滚动半径；in为变速器起动挡位的传动比；i0为主减速器的传动比；m为车质量；g为重力加速度；f为滚动阻力系数；θ为坡度角；CD为空气阻力系数；A为车辆的迎风面积；v为车速。

2 起步最优协调控制问题

2.1 起步最优协调控制问题的描述

选取发动机转速、离合器从动端转速和离合器传递转矩等作为状态变量，则状态变量X可表示为：

选取发动机转矩和离合器转矩变化率作为控制变量，则控制变量U可表示为：

则可将起步动力学方程（1）转换成状态方程的形式：

其中，

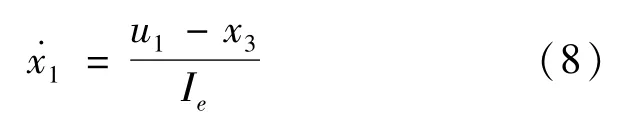
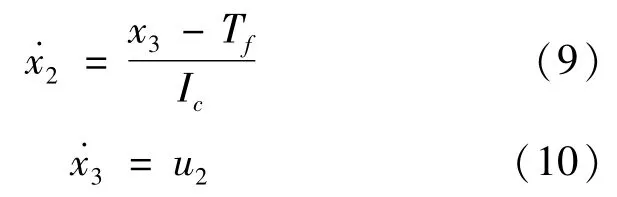
为适应驾驶员的起步意图，以驾驶员目标节气门开度下发动机输出最大转矩时所对应的转速为发动机目标转速。因此，在离合器主、从动部分的转速同步时刻（即滑摩期Ⅱ的结束时刻），状态变量x1需满足如下边界条件：

由离合器传递转矩连续变化所引起的车辆冲击度j可表示为：

由离合器摩擦片摩擦所产生的滑摩功W可表示为：

式中：t0和tf分别为滑摩期Ⅱ的开始和结束时刻。

为改善起步过程中离合器的使用寿命、起步平顺性及控制器能耗等起步性能，选取滑摩功、冲击度平方和控制能量消耗等的加权和作为优化目标J，其表达式为：

式中：Q1、Q2、Q3、Q4分别为优化目标中滑摩功、冲击度平方项、控制变量u1和u2的平方项的加权系数。

2.2 起步最优协调控制问题的求解

针对起步最优协调控制问题，引入拉格朗日乘子向量λ=［λ1，λ2，λ3］T，并构造广义目标泛函：

则Hamilton函数H（X，U，λ，t）为：

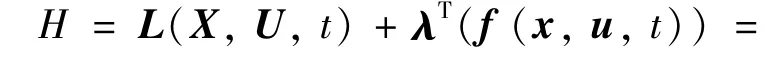
基于极小值原理可确定最优控制、状态及协状态变量需满足的最优性一阶必要条件，即状态方程（8）～（10）、协状态方程（17）～（19）和控制方程（20）～（21）。

协状态方程：

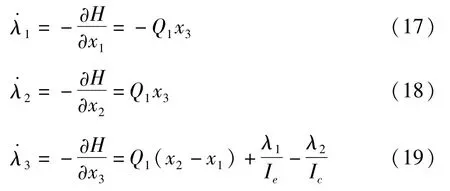
控制方程：

在初始时刻t0引入初始边值条件：

式中，we（t0）为发动机怠速工况下的初始转速；wc（t0）为零；Tc（t0）为等效至离合器从动端的车辆静止行驶阻力矩。

在结束时刻tf引入终了边值条件：

同时，引入协状态变量的横截条件：

2.2.1 边值问题的解析求解方法

针对基于极小值原理转化而来的微分方程组边值问题（即式（8）～（10））和式（17）～（24））进行数学推导求解，以获得最优控制、状态变量轨迹的解析表达式。

对式（19）进行一阶求导，并将式（8）（9）（17）（18）代入可得：

对式（25）进行一阶求导，并代入式（17）可得：

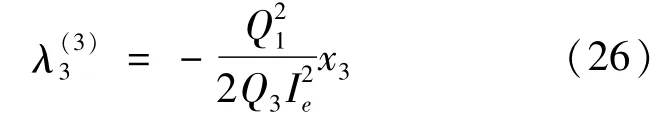
对式（26）进行一阶求导，并将式（10）和（21）代入可得：

式（27）是关于λ3的4阶微分方程，可得其解析解为：

式中：C1、C2、C3、C4为待定常系数；k1的表达式如式（29）所示。

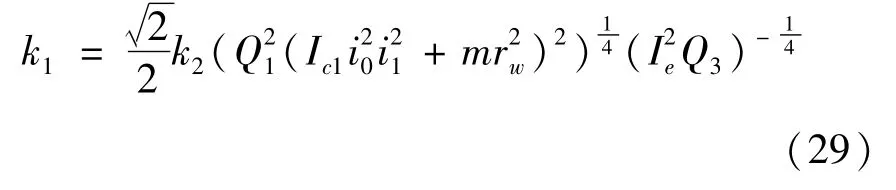
式中，k2的表达式为：

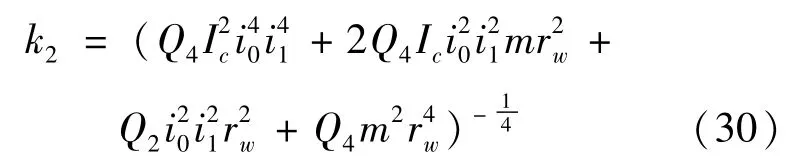
以式（28）所示的最优协状态变量λ*3的解析表达式为突破口，可逐一求解得到最优控制变量u*1、u*2，最优状态变量x*1、x*2、x*3和最优协状态变量λ1*和λ*2的解析表达式。具体推导过程如式（31）～（40）所示。

将式（28）代入式（21）可得u2*的解析表达式：

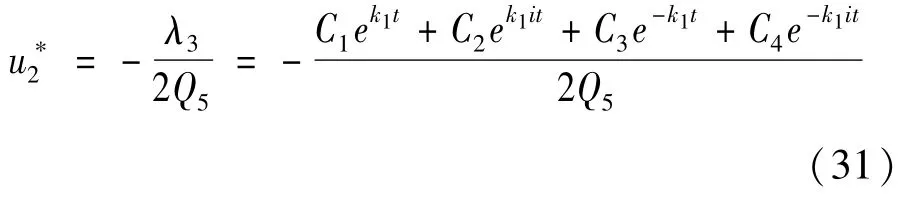
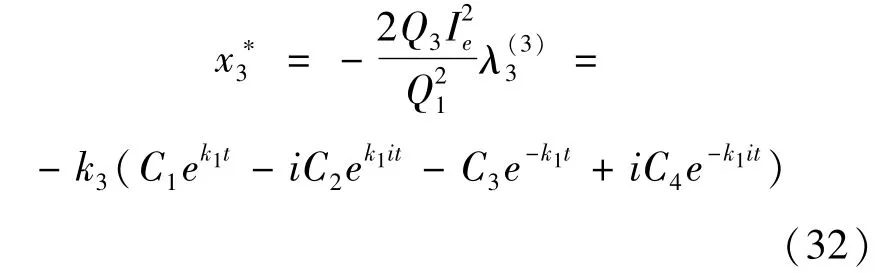
根据式（20）即可得u*1的解析表达式：

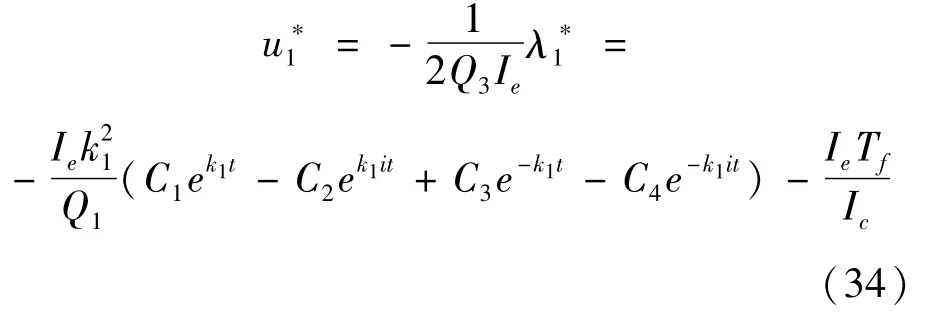
联合式（18）和式（32）可得λ*2的解析表达式：

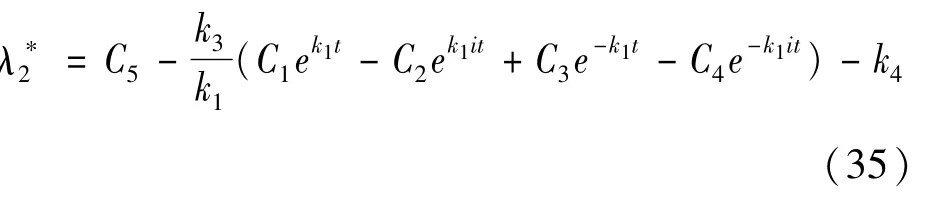
式中，C5为待定系数。

将式（32）代入式（9）可得x*2的解析表达式：

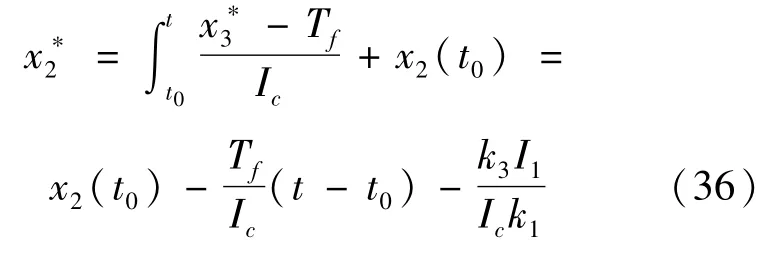
式中，

联合式（19）（28）（35）和（36）可解得x*1的解析表达式：

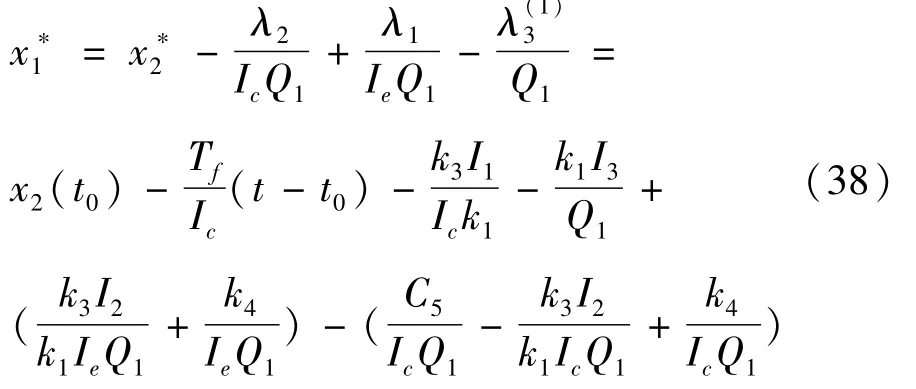
式中，

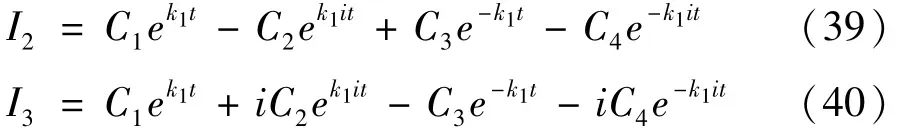
通过将边值条件（22）～（23）、横截条件（24）代入即可得到待定系数C1、C2、C3、C4、C5的值。

2.2.2 边值问题的数值求解方法

打靶法是求解微分方程组边值问题的一种有效数值求解方法，其实质是将微分方程组的边值问题转化为初值问题进行求解，并且通过不断迭代调整未知的初始条件，使迭代后的计算末值满足给定的终了时刻边值条件。基于打靶法对前文中的微分方程组边值问题开展数值求解的过程如图2所示。结合已有的状态变量初值条件和协状态变量未知初始条件的猜测值，通过状态方程、协状态方程和控制方程等进行数值积分计算得到状态变量与协状态变量的末值，并将计算末值代入终了时刻的边界条件及横截条件中计算比较，若偏差Δ在允许误差ε的范围内，则结束迭代过程；若偏差Δ超出允许误差ε的范围，则通过偏微商矩阵更新协状态变量初始条件的猜测值并重复上述过程。

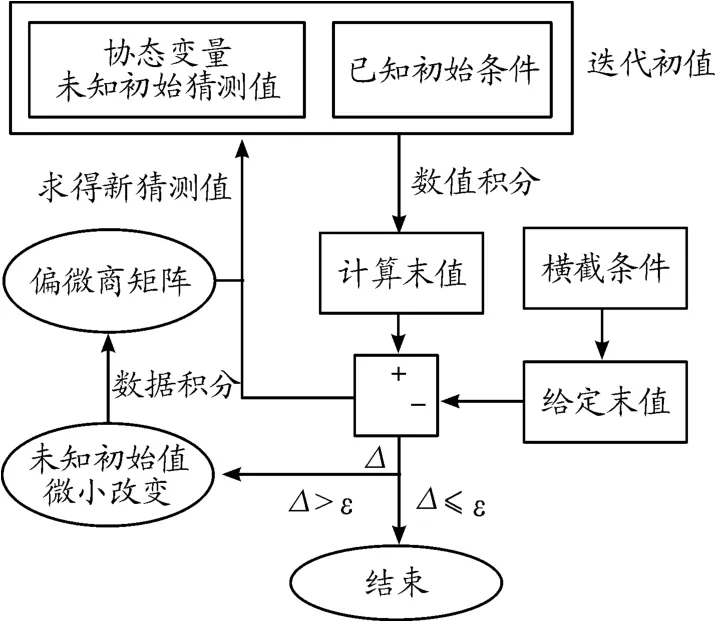
图2 打靶法求解过程框图

2.3 解析解与数值解比较

以某款配备了5速AMT的中型轿车为研究对象对其起步过程进行研究，其传动系统的主要参数见表1。

表1 传动系统的主要参数

在其起步过程中最优控制和状态变量轨迹曲线的求解过程中，优化目标中各项加权系数的选取是一个工程性很强的问题，一般依赖于专家经验及实车标定试验后的结果进行调整选取。基于经验，在节气门开度为20%下，选取各加权系数为Q1=1、Q2=1、Q3=8和Q4=6。

在Matlab R2013b的编译环境下分别采用解析和数值求解方法求得20%节气门开度下的起步过程半接合点后的滑摩期Ⅱ中的最优轨迹曲线，如图3所示。

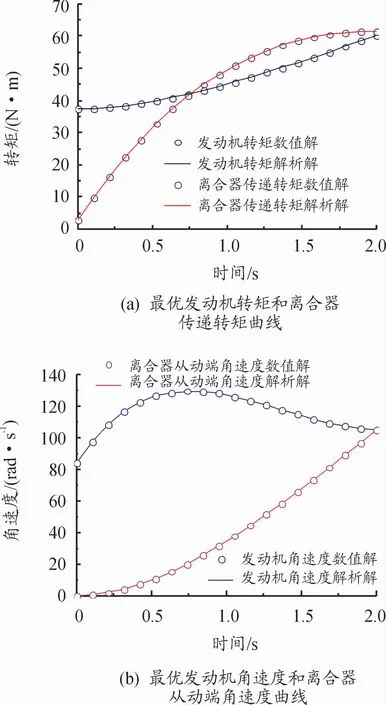
图3 最优控制轨迹解析解与数值解

离合器传递转矩随着接合压力的逐渐增加而逐渐增大，离合器从动端的转速也由零开始逐渐增大至与发动机转速同步（即车速由零开始逐渐增大至起步完成）。在前半部分，因发动机转矩仍大于离合器传递转矩，故发动机转速仍保持上升趋势；而在后半部分，为减小离合器的滑摩功，离合器传递转矩迅速超过发动机转矩，使发动机转速逐渐减小至与离合器从动端转速同步。对比图3中2种求解方法得到的最优轨迹曲线可知，两者的最大相对误差不超过0.2%。基于解析法和数值法求解计算最优轨迹曲线的时长分别为0.006 4 s和0.314 s，前者是后者的1/49，因此基于解析法的最优轨迹曲线更适于实时控制系统的应用。

3 AMT车辆起步硬件在环仿真试验

基于快速原型控制器Rapid-ECU-UIM 和Matlab/Simulink/RTW 平台搭建了AMT车辆起步的硬件在环仿真试验平台，并开展了不同加权系数组合及不同节气门开度下的AMT起步仿真试验以验证基于解析解的起步最优协调控制策略的有效性和实时性。

3.1 AMT起步的硬件在环仿真系统

基于快速原型控制器Rapid-ECU-UIM 和Matlab/Simulink/RTW 平台所搭建的AMT起步硬件在环仿真平台包括硬件和软件两部分。其中，硬件部分主要由快速原型控制器Rapid-ECUU1M、PC机、数据采集卡PCI-6024E等组成；软件部分主要包括AMT车辆起步的整车实时仿真模型、快速原型控制器中的起步最优协调控制模型及RTW 目标环境等。AMT车辆起步的硬件在环仿真系统的结构框图及实物图如图4、5。

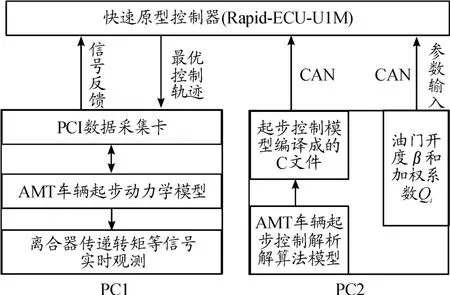
图4 硬件在环仿真试验系统结构框图

图5 硬件在环仿真试验系统的实物图

在AMT起步的硬件在环仿真试验中，PC2将基于解析求解方法的AMT起步最优控制模型编译成C文件并通过CAN总线下载至快速原型控制器Rapid-ECU-UIM中，将节气门开度和加权系数等作为起步控制器的输入参数；Rapid-ECU-UIM将求解得到的最优控制和状态变量的轨迹曲线通过PCI-6024E采集卡输入至PC1中所构建AMT车辆起步动力学模型作为控制输入；最后将仿真计算得到的数据反馈至控制器。

3.2 不同加权系数下的硬件在环仿真

在AMT车辆起步最优协调控制策略的设计中，优化目标中滑摩功、冲击度及控制能量等项的加权系数的不同体现了控制策略优化的侧重方向，会引起起步性能的变化。本小节通过保持优化目标中的加权系数Q2、Q3、Q4（即冲击度平方和控制能量等项的加权系数）恒定且为1、8及6，通过改变Q1（滑摩功的加权系数）以分析优化目标中加权系数的选取对起步性能的影响。Q1分别取0.6、0.8和1的硬件在环仿真试验结果如图6所示。

如图6（a）和（b）所示，不同加权系数下，发动机转矩、离合器传递转矩变化平稳，无明显突变。且在前半阶段发动机转矩明显大于离合器传递转矩，发动机转速迅速上升；在后半阶段离合器传递转矩逐渐上升至超过发动机转矩，则发动机转速迅速降低直至与离合器从动端转速同步以有效地减小滑摩功。如图6（c）和（d）所示，随着Q1的逐渐增大，即优化目标中滑摩功权重的逐渐增大，冲击度的最大幅值逐渐增大，而总滑摩功则逐渐减小，具体数据见表2。

表2 不同加权系数下的冲击度最大幅值与滑摩功

3.3 不同节气门开度下的硬件在环仿真

在节气门开度分别为20%和40%下进行缓起步与快起步的硬件在环仿真，结果如图7所示。

图6 不同加权系数下的AMT起步仿真试验曲线

图7 不同节气门开度下的AMT起步仿真试验曲线

如图7（a）和（b）所示，相比于20%节气门开度，40%节气门开度下起步要求更快，则发动机需求转矩更大，且目标角速度也随之增大。在节气门开度20%和40%下发动机转速与离合器从动端转速分别在2 s和1.55 s完成同步，此时发动机目标角速度分别为104.7、146.5 rad/s。如图7（c）和（d）所示，节气门开度20%和40%下冲击度均维持在较低水平，冲击度最大幅值分别为1.89、3.23 m/s3，均小于10 m/s3；起步过程的滑摩功分别为5.78、10.49 kJ。