次可加势函数拓扑压及因子映射

王威 高晓燕

(1.南通理工学院基础教学学院,南通,226002;2.南京师范大学数学科学学院,南京,210023)

1 引言

拓扑压是遍历论和动力系统研究的重点和热点.1973 年,Bowen[1]在度量空间中定义对于扩张映射的可加势函数的拓扑压,证明了拓扑压的变分原理.1975 年,Walters[2]在度量空间中得到了对于一般连续映射的可加势函数的拓扑压的变分原理.1988 年,Falconer[3]考虑次可加势函数在混合排斥集上的热力学形式,说明了如何用次可加势函数来研究非共形变换的动力学.2008 年,Cao[4]把Bowen[1]和Walters[2]的结果推广到一般紧致动力系统的次可加势函数上,给出了次可加势函数的拓扑压和变分原理.2020 年,Liang[5]利用因子映射给出了一个关于局部化拓扑压的半共轭公式.1958 年,Kolomogorov[6]引入了经典的测度熵和拓扑熵,之后,熵的研究便成了拓扑动力系统研究的的基本内容.

本文在Zhao[7]研究的次可加拓扑压的基础上引入因子映射,给出次可加势函数拓扑压的一个上界估计.

定义1([7]) 设(X,d)是紧致度量空间,T:X →X是连续映射,K ⊆X且K/=φ.对给定的常数ε ＞0,n ∈N,X的子集F称为X关于T的(n,ε)-生成集,若∀x ∈X,存在y ∈F,使得dn(x,y)≤ε,其中dn(x,y)=max{d(Tkx,Tky):k=1,2,···,n-1},X的子集E称为X关于T的(n,ε)-分离集,若∀x,y ∈E,x/=y,有dn(x,y)＞ε.

记rn(d,T,ε,K)为K的(n,ε)-生成集的最小基数,sn(d,T,ε,K)为K的(n,ε)-分离集的最大基数.定义

显然,r(d,T,ε,K)和s(d,T,ε,K)随着ε的减小而增大.令

易证h*(d,T,K)=h*(d,T,K)且与X上的度量无关,简记其为h(T,K),并称其为非紧集K上的Bowen 拓扑熵.

定义2([7])X上的实值连续函数族称为次可加的,如果∀n,m ∈N 和x ∈X,有fn+m(x)≤fn(x)+fm(Tnx).

∀n ∈N,ε ＞0 和次可加函数族,定义

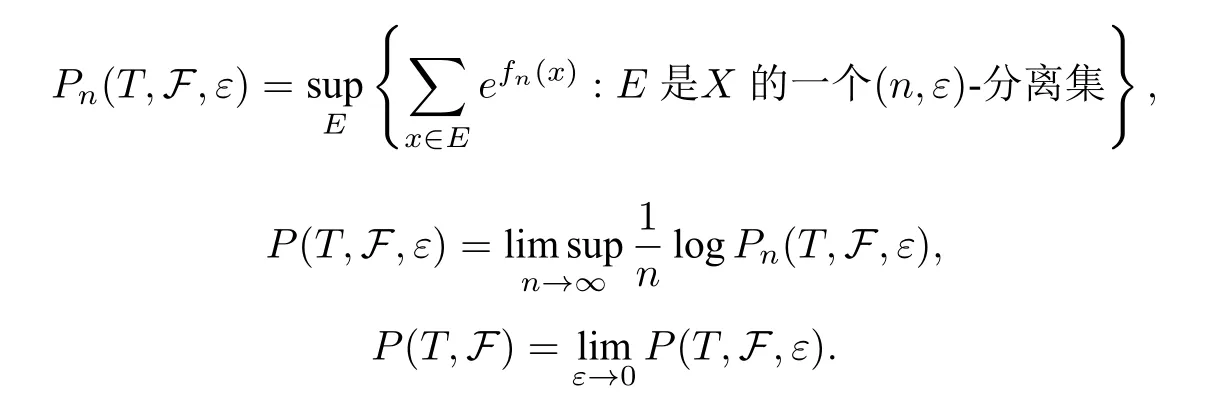
P(T,F)称作次可加势函数族F关于T的拓扑压,简记为

下面利用生成集定义次可加势函数族关于T的拓扑压.

∀n ∈N,ε ＞0 和次可加函数族,定义

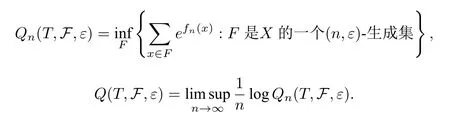
Q(T,F)=称作次可加势函数F关于T的拓扑压.

记Bn(x,ε)={y ∈X:dn(x,y)＜ε}.令ηn(F,ε)=supx∈Xsup{exp(fn(y)-fn(z)) :y,z ∈Bn(x,ε)}.如果满足Standing hypothesis,则有

命题1 ([7])设T:X →X是紧致度量空间X上的连续映射,F是次可加势函数族.若Standing hypothesis 成立,则有P(T,F)=Q(T,F).

定义3([8])设(X,T)和(Y,S)是两个拓扑动力系统,T:X →X和S:Y →Y是连续映射.连续映射π:(X,T)→(Y,S)称为因子映射，如果π是一一映射且满足π ◦T=S ◦π.

1971 年,Bowen[9]利用因子映射得到

2012 年,Fang 等[8]得到关于拓扑熵及因子映射的一个重要定理:设π:(X,T)→(Y,S)是因子映射,则对于任何集合E ⊆X

2013 年,Li 等[10]证明了:若π:(X,T)→(Y,S)是因子映射,φ:Y →R 是X上的实值连续函数,则对于任何集合E ⊆X,

其中h(T,π-1(y))=P(T,0,π-1(y)).

2 主要定理及证明

定理1设(X,T)和(Y,S)是两个拓扑动力系统,π:(X,T)→(Y,S)是因子映射,是Y上的次可加势函数且满足Standing hypothesis,则