基于大型停车场停车冲突的路径优化研究
2021-03-22周必扬常玉林
周必扬,常玉林,2,孙 超
(1.江苏大学 汽车与交通工程学院,江苏 镇江 212013;2.东南大学 城市智能交通江苏省重点实验室,南京 211189)
随着我国经济水平的发展,人们在大型商场的消费能力日益增长,加剧了商场停车的压力[1],因此,大型商场停车路径诱导优化问题越来越受到关注。目前,停车场路径诱导的研究主要集中在车位剩余提醒以及停车场外部的路径诱导[2],而停车场内部的路径诱导仅局限在标志牌的指示。因此,当遇到停车高峰期时,驾驶员往往只能靠盲目寻找,才能找到空车位,这不仅会导致汽车能源消耗的增加,而且会增加驾驶员的停车搜索时间。
在大型停车场的停车过程中,能够快速引导驾驶员找到合适的空余车位可以大大提高停车效率,缓解高峰时期停车场的拥堵程度[3]。目前,停车诱导系统作为ITS(智能交通系统)的重要组成部分,在欧美国家已经进行了大量的研究。Leephakpreeda[4]提出了基于模糊策略的泊车引导策略,其可应用于室外大型停车场的泊车引导;Zonkoly等[5]对停车场诱导系统的开发进行了理论研究;Fabian[6]对如何提升停车场内车位的利用率进行了研究。在国内,停车场引导系统的研究和实现主要集中在停车信息的采集、停车信息的发布以及停车路径的规划这3个方面。在停车信息采集方面,都是考虑采用无线传输的方式,例如wifi、蓝牙等传递车位信息[7-9]。停车信息的发布,也就是告知驾驶员停车场内空余车位的情况,目前对于这方面的研究相对比较多样,采用的是引导屏、广播、车载终端等。停车路径规划旨在引导驾驶员以较短的时间驶向空余车位,这已然成为当前的研究热点。张玉杰等[10]研究了使用Dijkstra优化算法,为驾驶员选择出最佳的停车车位,提高了停车场车位引导系统的智能化和人性化的程度[10];郭海峰等[11]在Dijkstra算法的基础上,研究了A*算法在停车场中的应用,以减少泊车用户盲目寻找车位所花费的时间,对大型停车场中的泊车路径规划有一定的参考价值。
上述研究虽然针对停车场内司机盲目寻找车位、停车耗时长等问题都有一定的优化,但都没有考虑到停车场停车冲突的问题,即前方车辆在停车时,可能会阻挡后车的通行。因此,针对上述问题,本文在Dijkstra算法的基础上,设计了一种考虑停车冲突的路径规划方法,以解决停车过程中后车因前车停车而产生冲突的问题,并通过Matlab进行仿真分析。
1 停车引导系统结构
人们在停车场的泊车过程可分为有引导过程的泊车和无引导过程的泊车。在无泊车引导的过程中,驾驶员通常会因盲目寻找车位或是找不到理想车位而耗费大量的时间,不仅会导致停车率低下,而且在高峰时段很有可能会导致停车拥堵。在有泊车引导的过程中,停车引导系统会通过算法,分配驾驶员目标车位所在的区域,通过车载语音提示指导驾驶员驶入目标车位[12]。
由于传统的停车引导系统只是告知驾驶员目标区域有空车位,但是没有提示驾驶员该车位是否有其他车辆驶入,也不会告知驾驶员该区域是否有其他车辆正在停车[13]。因此,当驾驶员根据停车引导的路线到达指定区域时,往往会出现以下2种情况:①该区域有其他车辆在停车,驾驶员需等待其他车辆完成停车后再进行停车;②该区域的目标车位被其他车辆率先停入。遇到第1种情况,驾驶员需要等待前车完成停车后,再驶入目标车位,遇到第2种情况后,驾驶员只能重新寻找空闲车位。以上2种情况均会降低停车效率,影响驾驶员停车时的体验性。因此,本文在传统的停车诱导系统上,增加了停车冲突模型,具体的停车引导流程如图1所示。

图1 路径规划诱导流程框图
当汽车进入停车场前,通常会进行车牌识别,这个过程是一个信息交互的过程。停车引导系统会根据停车场内空闲车位的情况,以距离电梯为最近的原则,采用Dijkstra算法,找到空闲车位,在进行车牌识别的过程中将车位信息以及停车场的布置信息传递到车上[14],然后汽车根据接收到的信息,进行语音提示路线。由于停车场内只涉及车与车位,可以认为是车-路-车的协同方式,通过V2X的路载设备和汽车进行通信[15]。假若出现跟车情况,后车因前车停车而等待时,且目标车位未被其他车辆占用时,后车上的停车引导系统会提前预测这个情况,以自车为中心,利用Dijkstra算法重新规划到目标车位的最短路线,并且同时计算等待时间和重新规划路程所需的时间,假若等待的时间大于行车的时间,则按照新路线至目标车位,若等待的时间小于行车时间,则等待前方车辆完成停车后再驶入目标车位。假若后车的目标车位,被其他车辆领先占有时,停车场中的路端设备会将信息传递到后车上,后车仍然以自车为中心,采用Dijkstra算法寻找距离最短的空闲车位。
2 停车场模型构造
大型停车场内进行停车引导,必须包含3个部分,即用户层、应用层以及感知层,如图2所示。感知层是停车场内用于感知汽车停车状况的,例如是否在停车,主要包含有红外传感器和WiFi模块等。应用层用于接收感知层的停车信息,分析停车场内的停车状况,判断有多少空闲车位,并将这些信息反馈给车辆,同时在车辆通过停车场入口时,利用Dijkstra算法决策出最短停车路径,传递给车辆。用户层就是车载应用,通过蓝牙、车载WiFi[16]接收应用层的车位信息,根据停车引导系统进行停车,同时将自身的停车情况提供给感知层的设备。
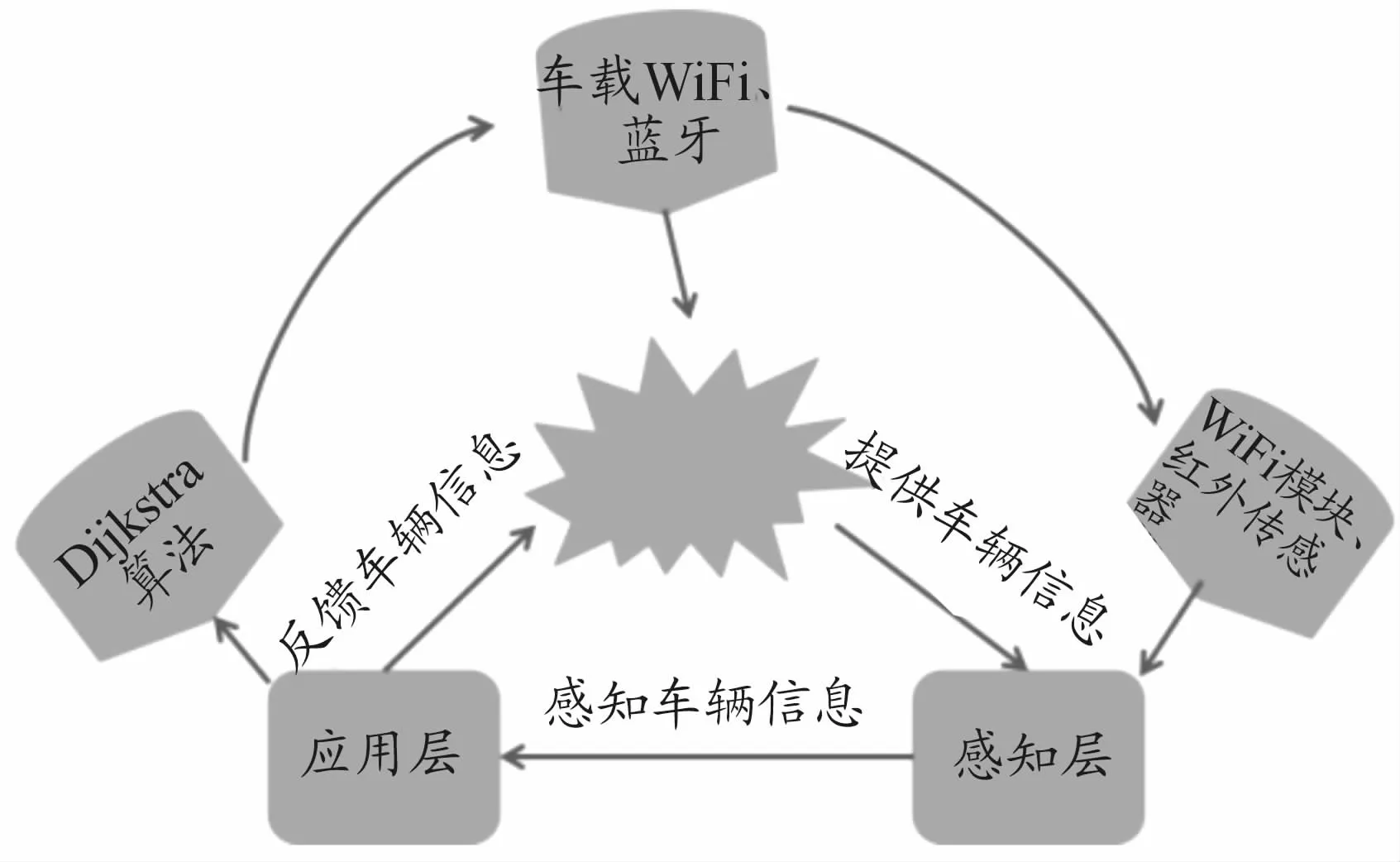
图2 停车场功能示意图
为了方便研究本文所提出的考虑停车冲突的Dijkstra优化算法,将停车场的内部结构简化为图3所示。图中Pi(i=1,2,…,15)表示空闲车位,①至⑨是用于安装路载设备的地方,位于停车场内的岔路口,检测不同区域内的停车状况。根据通车场内的交通流线,A、B、C、D、E、F表示停车的6个区域。按照停车场的一般设计,定义场内车位的宽为2.5 m,长5 m,道路的宽为5 m[17]。为了便于具体分析考虑停车冲突模型在路径引导中的应用,将图3中的入口、出口、电梯以及停车位简化为节点,图3所示的停车场结构示意图可转化为有向带权图,如图4所示。

图3 停车场结构模型示意图

图4 有向带权图
①至⑨在带权图中可以看作是到达空闲车位所需经过的节点,在带权图中只记录车位与车位之间的距离,通过带权图可以直观地体现各个空闲车位之间的距离以及停车路线。在运用Dijkstra算法进行停车路径搜索时,通常会将车位到人行出口的距离、入口到车位的行驶距离以及车位的安全性作为算法的主要依据,即道路权重因素[18]。本文的停车引导优化目标是减少停车时的等待时间,因此可以将路程段的平均时间作为辅助道路权重,以路程的距离作为算法的主运算道路权重。
3 基于冲突模型的Dijkstra算法
3.1 Dijkstra算法介绍
Dijkstra算法是目前停车路径优化中常用的算法之一,其工作原理是,从起始节点开始,依次搜寻其他最靠近的节点,并采用迭代检查的方式找到至目标节点最优的路径[19]。同时Dijkstra算法无法在考虑“车流量”的情况下,确定最优的停车位置,也就是在动态情况下,当汽车经过停车场入口后,仅凭Dijkstra算法无法确定是否有其他车辆停入了目标车位,因此需要配合停车场的路载设备,定点更新停车场的停车信息,并且使Dijkstra算法具有实时性,能够弥补其缺乏动态搜索的功能,给驾驶员提供更加合理的停车路径。
3.2 考虑停车冲突的Dijkstra算法模型优化和实现
根据图4所示的带权图,采用Dijkstra算法时,其搜索范围内空闲车位Pi距电梯的距离为Dis(R,ir),R车辆从入口至目标车位最短距离的集合,dR(i)表示其权值;Dis(s,is)表示行人从目标车位走至电梯的距离,s为行人从车位走至电梯的最短距离的集合,ds(i)表示权值[20];ηi表示目标停车区域产生停车冲突的权重。考虑到驾驶员在停车时,通常希望能够选择靠近电梯的车位。因此,基于距离电梯最近原则,定义最终权值γ为最佳车位的选择:
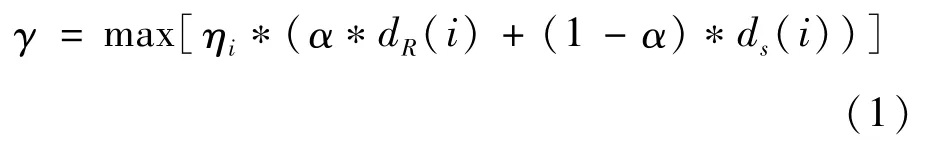
式中:α表示目标车位的地理位置权重,为固定值。若目标车位在电梯附近,则α为0.75,若不在电梯附近,则α为0.25,γ值越大表示车位的匹配程度就越高。定义矩阵dR(i,j)表示计算R时,以空闲车位为节点的邻接矩阵,dR中的元素i,j分别表示各相邻节点(Pi,Pj)间的权重值;矩阵dS(i,j)表示计算S时,以空闲车位为节点的邻接矩阵,dS中的元素i,j分别表示各相邻节点(Pi,Pj)间的权重值,若Pi,Pj不相邻,则矩阵中的元素置为∞。定义搜索区域为图5所示的①②④⑤、②③⑤⑥、④⑤⑦⑧以及⑤⑥⑧⑨这4个矩形区域,为了确保第一次搜索能够覆盖相对应的矩形区域,定义首次搜索以搜索中心所在的矩形区域的对角线的1/2所搜半径进行,具体的算法步骤如下[21]:
步骤1以电梯为中心、电梯所在矩形区域的对角线的1/2为半径进行搜索,若无空闲车位,则搜索半径每次增加20 m,直至找到为止。将所有搜索到的空闲车位集合记为P,每个空车位记为Pi,其中i∈[0,n-1],n为搜索到的空闲车位的节点数;
步骤2初始化最短路径集合R以及对应的最短路径权值dR(i),即R={R}、dR(i)=dR(0,i),其中i∈[0,n-1];
步骤3 选取Pk,使Pk={min dR(i)|P-R},所得的Pk就是当前求得的一条从R出发的最短路径终点,将Pk加入到集合R中,即R={R,Pk};
步骤4更新从R到Pk的最短路径权值,令dR(i)=min{d(k),dS(i,k)};
步骤5重复步骤3和步骤4,直至空闲车位集合P的节点全部包含在集合R中。
步骤6 初始化最短路径集合S以及对应的最短路径权值dS(i),即S={S}、dS(i)=dS(0,i),其中i∈[0,n-1];
步骤7以步骤2至步骤5的方法,将空闲车位集合P的节点全部包含在集合S中;
步骤8根据式(1),计算筛选出集合P中的所有空闲车位的最终权值,数值最大的则为最优泊位Pbest,相应的dbest(i)所对应的路径即为从入口到最优泊位Pbest的最短路径。
步骤1至步骤8解决的是单车情况下的停车工况,在节假日等停车高峰时段,上述Dijkstra算法已经不能够满足停车场内的动态路径引导。因此,本文在Dijkstra算法的基础上,提出了考虑停车冲突的动态停车路径引导算法。
当考虑停车场内的动态交通流,同一停车区域有2个空闲车位时,规定停车场内汽车平均以Vj=15 km/h的车速行进,停车时的平均车速为5 km/h,车辆到达目标车位停车所需的时间平均为20 s,当停车完成至3/4时,后车便可通过[22],后车在给定的泊位Pbest的最短路径上行驶,相应的算法如下所示:
步骤1计算前车从停车区域的分岔口到目标车位的时间Tf=Lbest/Vf,其中Lbest为最优泊位Pbest到区域分岔口的距离;
步骤2计算后车到达区域分岔口的时间Tb=Sbest/Vf,其中Sbest为后车根据上述步骤1至步骤8得到的最优泊位至入口的距离;
步骤3计算后车经过前车目标车位所需的停车等待时间,其中Hbest为前车未到达目标停车区域前的行驶距离,且Hbest=Vj*tf,tf为前车进入停车场的时间;
步骤4判断时间差ΔT是否大于20;若大于20,则以自车作为起始节点,代替步骤1中的入口节点,以20 m为起始半径,逐次增加20 m,按照步骤1至步骤8搜索出最优泊位Psec和dsec(i)对应的最短路径;
步骤5计算步骤4中到达目标车位所花的时间
步骤6判断Ta与ΔT的大小,若Ta大,则后车不改变原有的停车路径,等待前车停车,然后再驶向目标车位;若Ta小,则按照步骤4,后车重新规划停车路径,以避免停车等待的时间。
4 仿真结果与优化
4.1 单车仿真结果
按照上述优化算法的思路,以Matlab为工具,对本文中提出的基于停车冲突的引导系统的最佳泊位进行选取。以图3作为某一时刻停车场空闲泊位的分布图。系统对剩余的10个空闲车位信息进行存储,对它们之间的路径关系进行存储,结合本文提出的优化算法,在停车场后车对前车进行跟车的情况进行仿真,假定从后车经过入口算起,当前车经过分岔口④时,后车与前车距离为10 m,其仿真结果示意图如图5所示。
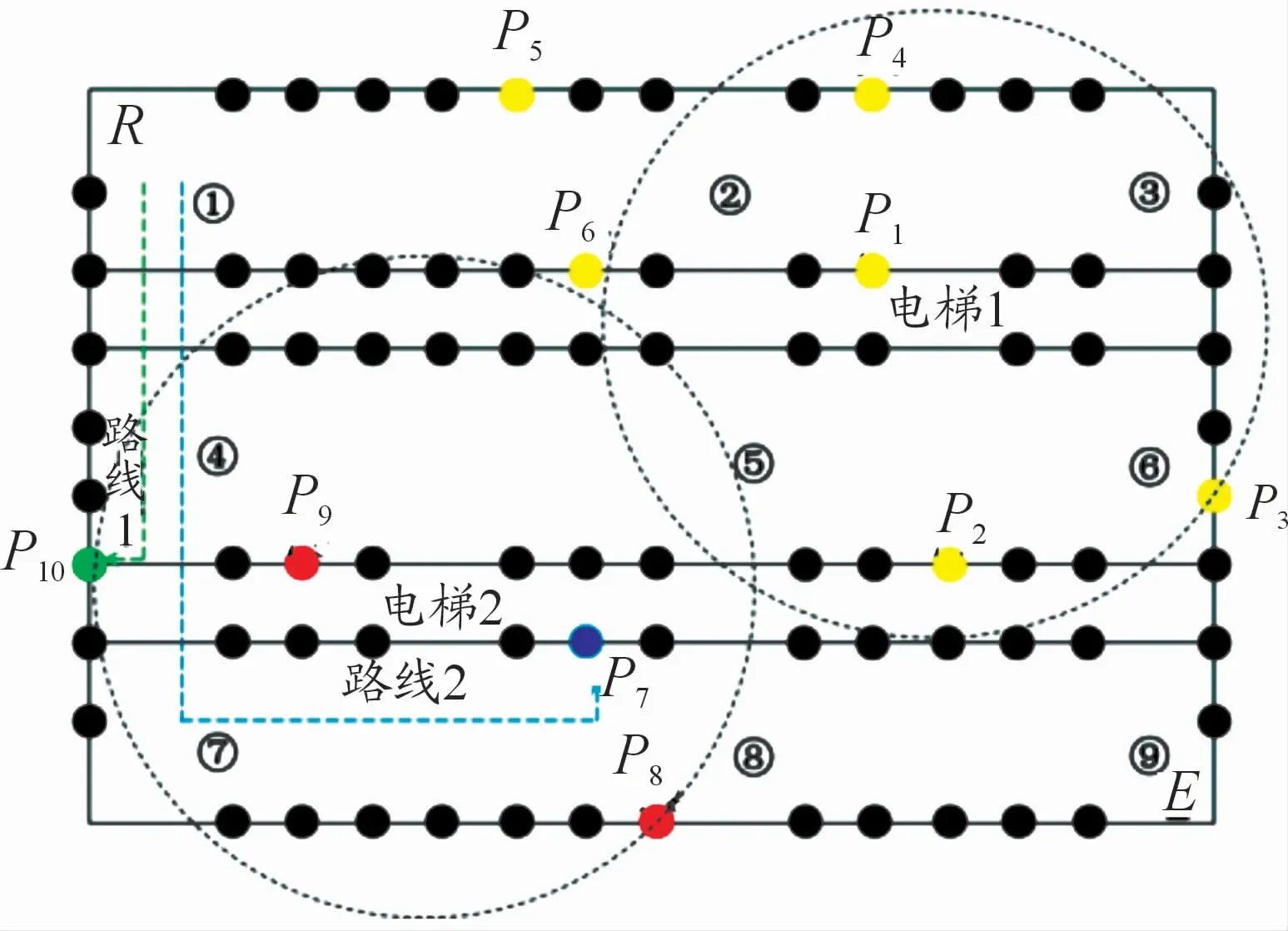
图5 仿真结果示意图
对2个电梯进行随机选择,以电梯2作为前车的搜索中心。根据改进的Dijkstra算法,将前车的目标车位限定在圆形内,并且计算出的最优路径为路线1,目标车位为P8P1P2P3;当后车经过入口R时,计算出P6的最优路径为路线2,目标车位为P7。Dijkstra算法搜索范围内的目标车位及停车信息如表1所示,前车与后车的停车路线信息为:前车目标车位P10,前车停车时间23.4 s;后车目标车位P7,后车等待时间17.6 s,后车停车时间41 s。
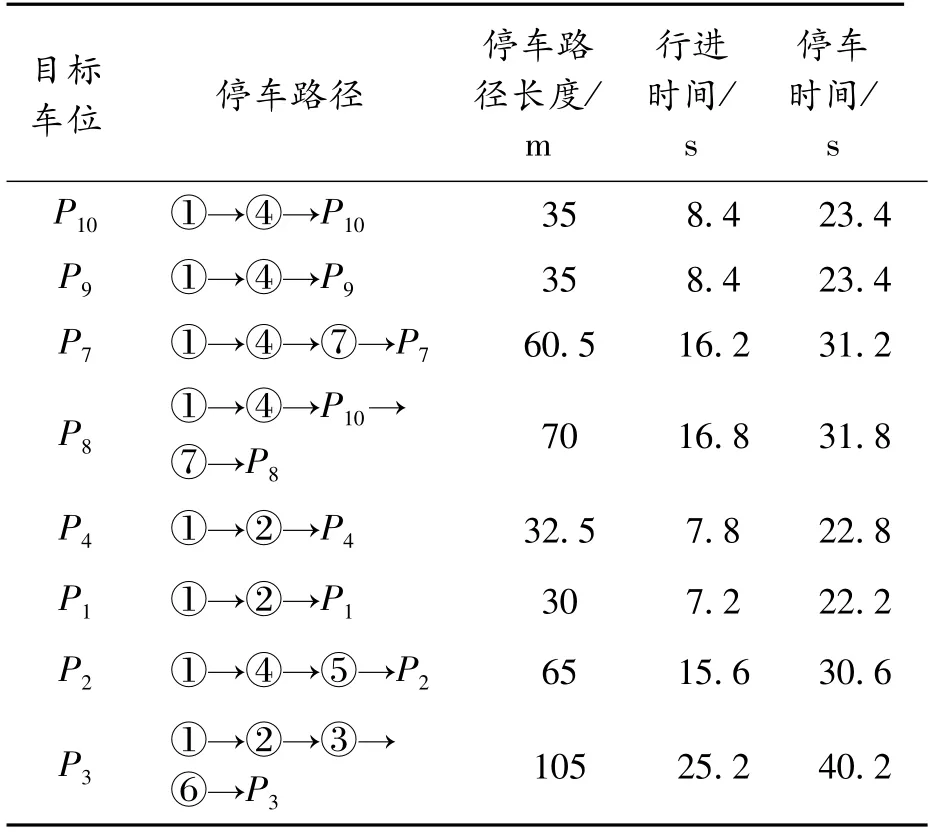
表1 停车时间及路径信息
从表1中可以看出,目标车位为P10和P7,停车时间相同。而考虑跟车情况下的停车工况,后车等待前车停车的时间,占了停车总时间的38%,停车耗费的时间过多,并且在节假日还会造成停车拥堵。因此,当遇到前车停车导致后车等待时,通过本文中提出的算法,得到后车路径的优化,如图6所示,优化后后车的停车数据如表2所示。
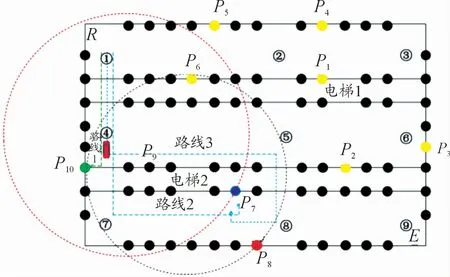
图6 优化后停车路线示意图

表2 优化后后车停车数据
从图6中可以看出,以后车为中心的Dijkstra算法能够准确地找出目标车位,在其搜索范围内,找到2条路径能够避免停车等待,并且仍旧遵循靠近电梯的原则选择车位。从表2中可以看出,优化后的停车时间缩短,就目标车位P7来说,优化后的停车路径为线路3,算上后车经过入口的距离,虽然行驶的路径要比原先路线2长,但是停车时间要远比原先路线2的时间短,能够大大减少驾驶员的停车时间,从而提高停车效率。
本文中所提出的基于停车冲突模型的Dijkstra算法是建立在停车场内的跟车工况下的,因此跟车距离的大小,能够很大程度上影响后车停车效率。根据第三部分提出的算法,可知后车的等待时间为:

式(2)表示的是后车等待前车停车的时间,其中x为前车到达分岔口时,后车与前车的车距。从式(2)可以看出,后车的等待时间与车距成反比,当前后两车相距62.6 m时,后车不需要等待。因此当上述算法中Sbest-Hbest<62.6时,需要进行步骤1至步骤7,为后车重新制定停车路径。在实际的停车场内,通常是多车跟车的停车工况,因此还需要将仿真做进一步优化。
4.2 多车仿真结构
在考虑多车跟车的停车工况时,在步骤1至步骤7中导入跟车距离[23]:

式中:Si表示前车和后车之间的跟车距离;ti为后车遇到停车干扰时所用时间;tn表示后车在无前车停车的干扰下,停入目标车位所需的时间;t(n-1)表示前车在无其他车辆的干扰下,停入目标车位所需的时间;xn(t)表示后车到目标车位的路径长度;xn-1(t)表示前车到目标车位的路径长度。
假定图5所示的停车场在区域①②④⑤⑦⑧内有15个空闲车位,且含有多辆车进行停车。多车仿真是为了检验本文提出的模型在提高停车效率中的合理性,考虑到在停车场的实际交通流中,车与车之间存在的交互情况会对停车时间造成影响,本文在加入跟车模型之后,需要计算前方有车正在停车而造成仿真过程中后车等待的时间。因此,加入跟车模型之后的停车时间由等待时间以及停车行驶时间两部分组成。在上述的算法中加入跟车模型后,在Matlab中将采用本优化算法和采用优化算法这2种情况下的停车时间、停车数量以及停车等待时间进行比较,设置5条停车路径,停车区域内包含10辆车,在进行停车或是正在行驶中,基于上述的步骤1至步骤6,具体仿真结果如图7和图8所示。

图7 优化前停车时间、停车数量以及停车等待时间关系
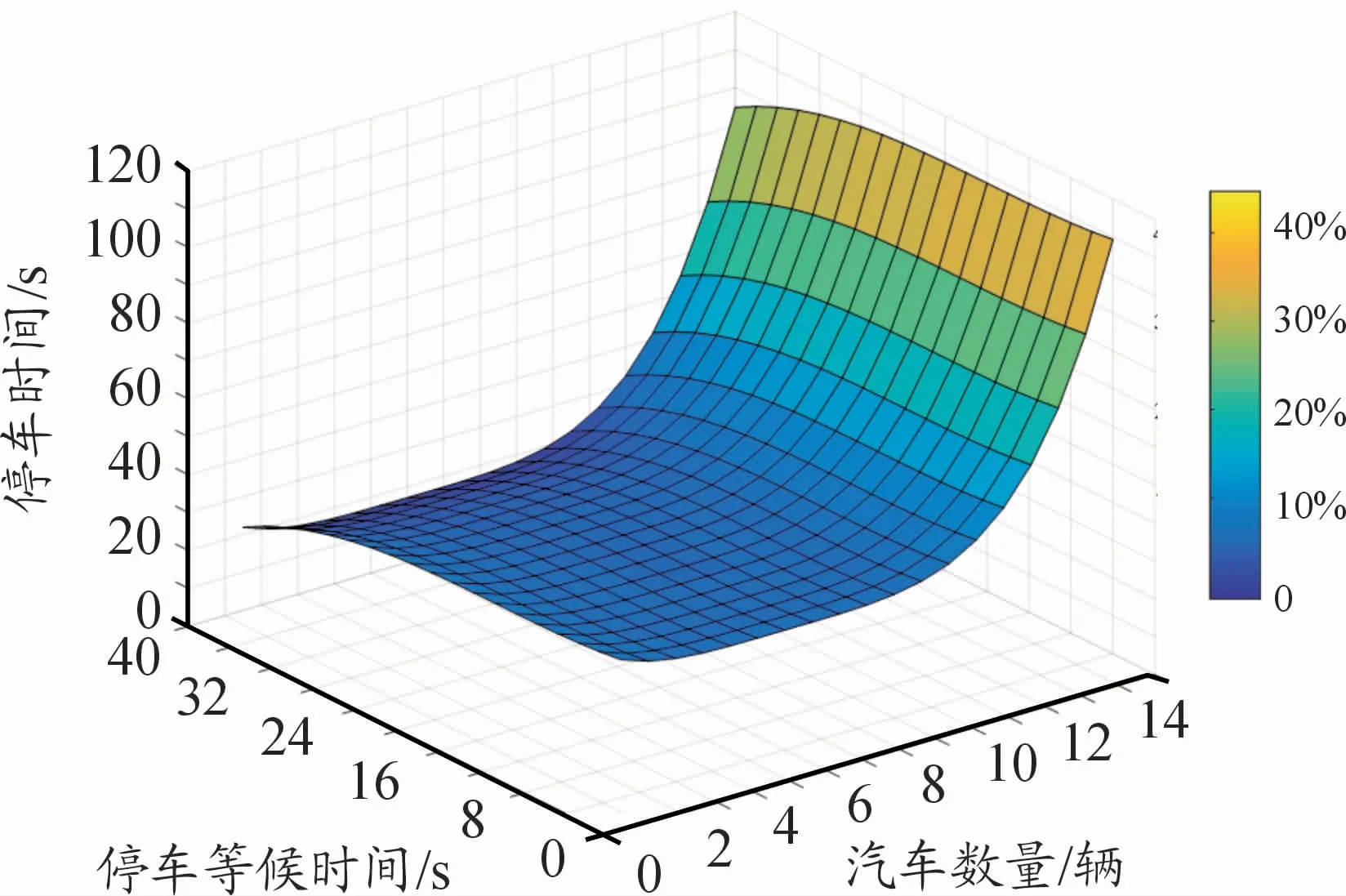
图8 优化后停车时间、停车数量以及停车等待时间关系
从图7中可以看出,当本车的目标停车路径上有其他车辆正在进行停车,本车选择等待,花费的停车时间最高可达118 s,其停车等待的时间为46 s,占总时间的39%,其停车通畅率最高只有61%。而从图8中可以看出,加入本文提出的算法之后,本车停车时间最高为108 s,对应的停车等待时间为18 s,占总时间的16%,显然采用优化算法后的总的停车时间减少了8%。
根据图7及图8,结合Matlab仿真,将优化前与优化后的停车路径长度进行比较,如表3所示。

表3 停车路径及时间
从表3中可以看出,优化前在给定的车辆数中,停车路径上的行车通畅率平均在71.8%左右,驾驶员在停车的过程中,将近有30%的时间花费在停车等待中。而优化后在给定的车辆数中,平均通行率为88.6%左右,相比于优化前,停车等待的时间减少了17%,优化率幅度60.7%。从表3中还可以得知,当停车路径上的车辆数少于9辆时,经优化后的汽车可以完全避免停车等待,当停车路径上的汽车大于9辆时,超过了停车路径所能承受的最大车辆数,即便经过优化后也不能完全避免停车等待,但是能够减少停车等待的时间,这对于停车场来说,能够缓解高峰时间的停车拥堵。因此,当停车路径上的车辆数小于最大车辆负荷数时,本文提出的动态Dijkstra算法能够避免停车等待的时间。
5 结论
通过分析大型停车场结构特点以及场内跟车状况,把大型停车场简化为有方向的带权图,在考虑后车进行跟车的基础上会出现等待前车停车的状况,在改进Dijkstra算法的基础上,考虑了动态的停车工况,当后车出现停车冲突,需要进行停车等待时,以后车自身为中心进行车位搜索,从而达到实时改变停车路径,以便驾驶员绕过停车拥堵的路段,避免停车等待。通过在Matlab中的仿真结果分析,考虑停车拥堵的Dijkstra算法实现了“空间换时间的功能”,增加停车路径的长度以避免停车等待的状况;当停车场内停车路径上的汽车数量未达到最大限制时,能够完全避免停车等待;当汽车数量超过最大限制时,可以减少停车等待的时间。这对提高大型停车场的车辆通行效率有参考价值,尤其是节假日时期,可减少因停车数量多导致停车等待产生的停车拥堵的问题,对提高大型停车场内的行车通畅率有重要意义。
本文中提出的停车冲突模型只是考虑了停车场一个入口和一个出口的情况,在实际的停车场中,往往包含有多个入口及出口。因此,未来的研究内容可以在多个出入口的基础上,对动态停车模型做进一步的研究。
