追求理想，始于疑问

丁伯军

[摘  要] 以帮助教师和学生过一种幸福完整的教育生活为目标的新教育实验在我国中小学已经实施20年，给我国的教育带来不小的改变. 研发新课程、研读新课标、构筑新课堂是成为新教育时代一名合格教师所必须践行的. 构筑新教育理想课堂是一线教师不懈的追求，参与度、亲和度、自由度、整合度、练习度、延展度这六个维度是课堂教学的目标，同时也给新教育理想课堂的构建提供依据.

[关键词] 新教育;问题;章节起始课;初中数学

章节起始课是学习发生的开始，是知识生成的“萌芽”，是每章教学内容的“开场”. 对于初中数学而言，章始课能给学生展现每章学习内容的知识脉络，引领本章学习内容的方向及目标，在章节学习中起着统领的作用;同时，数学知识都不是孤立存在的，数学知识的自然生长都遵循着系统性原则，章始课也是原有知识的延展与升华，因此章始课“启下”的同时也发挥着“承上”的作用. 数学是一门以解决问题为主要任务的学科，问题的提出与解决贯穿于整个课堂，问题也承载着学生知识及智慧的发展，新教育理想课堂的构建离不开问题的串联，章节起始课更是依托“疑问”来承接前后知识.

课题引入——生疑

良好的开端等于成功的一半，课题引入是新授课的第一步，引入环节的目标是将学生“领进门”，让学生对本节课的内容产生期待. 激发学生学习数学的兴趣往往从学生主动质疑开始，问题能够调动学生学习的积极性，解决问题能够激励学生不断去探究新的知识.

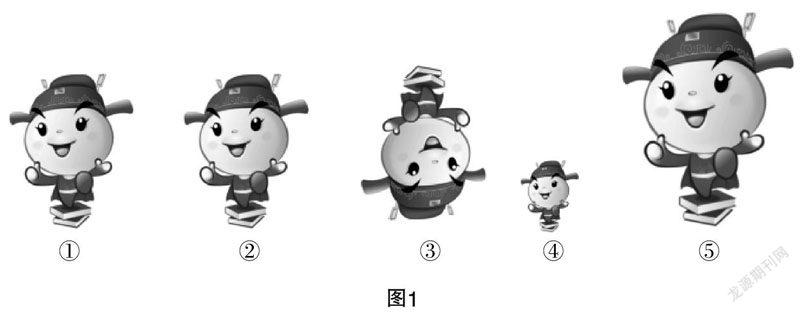
如27章的起始课“27.1图形的相似”（人教版，下同）中，课题的引入首先呈现图1中的图片，让学生观察图片①与图片②及图片③的关系，回忆全等图形的定义：“能够完全重合的两个图形叫做全等形”，回顾全等图形必须满足两个条件：“形状相同、大小相同”;在回顾旧识的基础上再让学生观察图片④与图片①、图片⑤与图片①的关系，引导学生从全等条件出发思考问题，发现全等条件的缺失，从而对这样形状相同、大小不同的图片之间的关系产生疑问，在此基础上引入相似的定义，揭示课题.

新教育理想课堂的创建很大程度上体现于对学生核心素养的培养，而质疑能力是发展学生数学核心素养的前提及重要保障. 课题引入环节承担激发学生质疑能力的主要责任，让学生对知识主动生疑，是一种有效的启迪与赋能.

新知建构——探疑

知识建构是新授課的中心环节，是新知识开始发生的过程，也是体现新教育理想课堂中参与度及自由度的过程. 在章节起始课中，新知伴随着疑问而展开，学生对新知的构建是一个探疑的过程.

以“22.1二次函数的图像及性质”为例，在新知构建环节，让学生类比一次函数的学习方法展开对二次函数的研究，引导学生从“数”和“形”的角度探究二次函数的图像及性质. 在教学实践中，主要围绕以下四个问题进行探讨：

1.？摇你能从“数（解析式）”的特点来想象出“形”的特征吗？

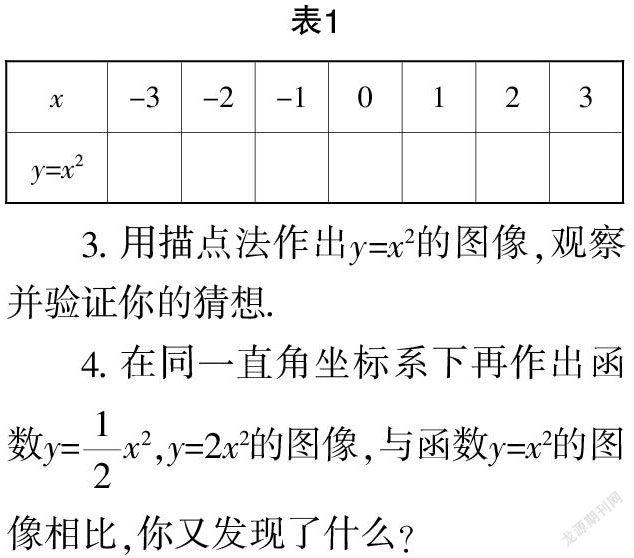
2.？摇填写如下表格，并观察对应的坐标关系，概括你的发现.

3.？摇用描点法作出y=x2的图像，观察并验证你的猜想.

4.？摇在同一直角坐标系下再作出函数y=x2，y=2x2的图像，与函数y=x2的图像相比，你又发现了什么？

上述问题由教师提出，但探究任务全部交由学生，通过自主思考、小组合作的方式完成问题的解答及知识的建构. 问题由抽象到具体再到抽象，难度逐渐加深，不断引导学生对新的疑问进行试探，新教育理想课堂的参与度与自由度得以体现.

方法提炼——释疑

在数学学习中，掌握知识固然重要，但方法的提炼在某种程度上比知识的掌握更为重要，学习应该在知其然的同时知其所以然，掌握方法才是真正理解知识并学会学习. 新教育理想课堂将方法的提炼作为数学教学的重点，从问题的角度来看，方法的提炼有助于问题的自然辨析与深入理解，是释疑的过程.

以下是笔者在教学“18.1.1 平行四边形的性质”中与学生对话的片段.

师：我们探究平行四边形的性质主要是去分析它的哪几个元素？

生1：我们应该去分析它的边和角.

师（追问）：为什么？

生1：我类比了三角形性质的探究方法.

师：非常好，你学会了知识的迁移. 那谁能更具体地谈谈分别从哪些角度去分析四边形的边和角？

生2：我们可以探究一下平行四边形的对边和邻边在位置及长度上分别有什么关系，同时探究一下四边形的对角和邻角之间的度数有什么关系.

师：你分析得真是透彻，三角形与平行四边形同属于多边形，他们的探究方法是相通的. 但是四边形和三角形相比，还多了一个元素，是什么呢？

生3：对角线.

师（追问）：我们从哪个角度研究对角线呢？

生4：我们可以研究对角线的位置关系及长度关系.

师：太棒了，同学们对于如何探究平行四边形的性质都有了系统完整的想法，下面我们就从这些边、角、对角线出发，小组合作来共同探究平行四边形的性质.

从边、角、对角线这三个角度去猜想和分析多边形的性质是几何图形常用的探究方法，在初中阶段的平行四边形和特殊四边形学习中最为常用. 在上述师生对话中，虽然学生回答得并不完美，但学习方法的掌握已得到体现，学生主动探究知识及自主学习能力得到发展. 在对上述问题的思考及分析中，学生的疑问逐渐消除，知识方法自然得到内化. 从新教育的视角来看，学会学习比掌握知识更为重要，方法的提炼凸显理想课堂的自由度和整合度.

知识关联——拓疑

每节课的时间是有限的，但是知识却是无穷的，初中数学课堂常常以课堂小结作为新授课的最后一个环节，但小结只是对这节课内容的概括与总结，它更多地倾向于对后续知识的延展与升华，而不是知识的终结. 诚然，疑问最能激发人的探究欲望，章节起始课担负着引领整章学习的重任，更应注重对学生知识及思维的延伸，因此新教育理想课堂倡导以疑问的拓展作为课堂小结的形式，以此助推学生高阶思维的发展.

例如章始课“8.1二元一次方程组”的教学中，以概念教学为主，主要学习任务是厘清二元一次方程、方程组、二元一次方程组的概念，并明晰二元一次方程的解及二元一次方程组的解，难度不大. 在课堂小结中，除了对上述知识进行总结以外，可以设置如下问题：

1.？摇你觉得我们为什么要学习二元一次方程组呢？

2.？摇你觉得我们接下去将学习什么内容？

3.？摇你对本章的学习有什么规划吗？你将如何展开本章内容的学习？

4.？摇学完本章知识，你觉得我们以后还会学习哪些与它相关的知识呢？

在教学实践中，笔者给予学生足够的时间去思考及讨论上述问题，让学生经历“为什么学”“学什么”“如何学”的过程，使学生对本章的内容与结构有整体的把握，同时思考并分析研究方法，学会知识的类比与方法的迁移，以形成自己的研究思路，为学好本章内容及后续内容做好铺垫. 数学知识紧密关联、环环相扣，数学学习追求数形结合、前后联系，数学教学应关注知识关联、方法关联. 章始课的教学更应注重问题的拓展，让学生学会本节课知识的同时能够产生新的疑问，让知识得到延展，让思维得到升华.

在实践中笔者越来越深刻地感受到，章始课不但是知识的开始，还是方法的延续;不仅是能力的发展，而且是潜能的激发. 章始课的教学不但要关注知识的引领，更应关注内容的整合，同时还要注重方法的引导. 章始课的教学实施可以通过创设问题情境、小组合作、实验操作、数学游戏等方式，由疑问开始并贯穿于整个教学过程，让学生通过观察思辨、自主探究、相互交流、动手实践等方式经历知识发生发展的过程. 教学中学生对疑问不断试探、不断深入，让数学核心素养渗透于整个课堂，让学生的知、行、意得到全面发展，让新教育理想课堂的内涵落地生根.

3836501908245