整体试商，提升思维素养

鲍善军

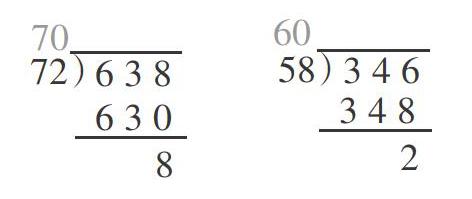
[摘 要]除数是两位数的除法的计算过程比较复杂，是学生的学习难点。以整体感知教学的视野重新审视单元内容，从整体试商的角度对教材内容进行重构，使学生在具体情境中真正认识到运算的作用，从而体会运算的价值，提升自身的思维素养。

[关键词]试商;除法;思维素养

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2021）05-0055-02

【教学内容】人教版教材四年级上册“除数是两位数的除法（试商）”

【课前慎思】

除数是两位数的除法，是小学整数除法的最后内容，它的计算原理与除数是一位数的除法相同，只是试商的难度加大，计算过程比较复杂。为解决笔算除法试商这个关键问题，教材按照计算的难易程度分两段编排：

第1段：商是一位数，分3个层次：用整十数除;除数接近整十数;除数不接近整十数。

第2段：商是两位数，将商是一位数的除的过程、试商方法等迁移至此。

其实，学生在学习除数是一位数的笔算除法时，已经掌握了除的顺序、商的书写位置、余数必须比除数小等基本规则。分析前测结果（40名学生参加）得知：60%的学生能正确笔算“除数是两位数的除法”中商是一位数的除法，部分学生暑假期间已学过;27.5%的学生能正确笔算“除数是两位数的除法”中商是两位数的除法，但只有15%的学生能基本表述其算理和算法;大部分学生笔算“商是两位数”的除法时出现试商困难和商的位置模糊问题。

基于以上认识，笔者以整体感知教学的视野重新审视单元内容，从整体试商的角度对教材内容进行了重构：

第一课时：除数是整十数的两位数除法。学习内容是“口算除法，商是一位数的笔算除法，商是两位数的笔算除法中商的书写位置、除的顺序，以及商末尾有0的除法”，帮助学生理解笔算的算理。

第二课时：除数是两位数的除法的试商。学习内容是“基本试商方法，灵活运用试商方法”，培养学生灵活计算的意识和灵活解决问题的能力。

【课中深思】

一、复习铺垫，引入新知

口算：40×7=    30×20=   60×90=

480÷60=        210÷30=      500÷25=

42×7≈    28×21≈   66×99≈

480÷58≈   210÷32≈ 500÷26≈

师：大家在计算时是采用怎样的方法估算的？

生1：把42、21、32这些数估小成整十数，把28、99、58这些数估大成整十数。但是，66×99和500÷26这两道题比较特殊。

生2：估算时一般情况采用四舍五入法估成整十数，像66×99和500÷26这样的要特殊对待。

师：你们概括得太棒了！估算时，一般按照四舍五入法把一些数看作和它接近的整十整百数，特殊情况要学会灵活估算。这节课，我们就带着这样的数学思考继续学习“除数是两位数的除法”。

【设计意图：乘除法估算方法的概括承上启下，能引导学生观察数据的特点，为后续四舍五入法试商和特殊情况下灵活试商的学习做好铺垫。】

二、解决问题，展学讨论

材料一：四（1）班举行班队活动，乐乐和明明帮老师准备奖品。一个笔袋21元，乐乐带了84元，可以买多少个？一个台灯62元，明明带了430元，可以买几个？还剩多少元？

师：分别列竖式计算，并想想是怎样试商的。

生1：对于第一问，我先把除数21看作20，84里面有4个20，所以商4，再用4乘21，刚好是84。

师：说得真好！但为什么要先把除数21看作20？

生1：把21看作20这样的整十数，计算时更加简便。

师：是啊！整十数让我们在试商时更加一目了然。那第二问也可以这样处理吗？

生2：把62看作60来试商，430里面有7个60，所以商7。再算7乘62等于434，积比被除数还大，说明商7大了……

师：商7大了，怎么办？

生2：商大了，要把商调小，改商6。

师：真棒！商大了，就要调小。

师：我们刚才都是把除数估小成整十数，那是不是其他问题也可以这样解决呢？

材料二：学校报告厅每排有28个座位，六年级共有197人，可以坐满几排？还剩几人？

师：列竖式解题，并思考是怎样试商的，试商过程中遇到了什么问题。

生3：把28看作30，197里面有6个30，所以商6。再算6乘28等于168，相减得到余数是29……

师：余数是29，可以吗？

生3：不可以，余数29比除数28还大了，说明商6小了。

师：把28看作30，商6小了，该怎么办呢？

生（齐）：要调大，改商7。

师：是啊！商小了，就要调大。

师：我们来总结一下，除数是两位数的除法的试商方法来怎样的？

生4：除数是两位数的除法，一般按照四舍五入法，把除数看作和它接近的整十数来试商。

生5：我發现试商和估算都是用四舍五入法，把一个数看作和它接近的整十数。

师：确实，试商就是估算的一种应用。

【设计意图：学生在独立尝试、互动交流的过程中，都能理解并掌握基本的试商方法，进而沟通试商与估算之间的知识关联，接受事物之间相互联系的观点。】

师：计算下面各题，你有什么发现？

[12）] [1 0 8][39）] [3 1 2][48）] [4 2 5][53）] [5 2 6]

生6：我发现这些题的商都是8或者9。

师：仔细观察这些数的特点，还有什么发现？

生7：被除数和除数最高位上的数相同，并且被除数的前两位比除数小。

师：被除数和除数最高位上的数相同，说明它们之间的倍数接近——

生8：接近10倍。

师：被除数的前两位比除数小，说明它们之间的倍数是比10倍小一点，所以商是——

生9：9或8。

【设计意图：通过引导学生观察数，培养了学生的估算能力，使学生明白了其中的算理，还为下一环节的灵活试商提供了参照素材。】

三、引发冲突，深入探究

材料三：周老师给四年级结对的同学寄快递，每件特快专递26元，周老师带了240元钱，可以寄多少件特快专递？

师：解题，并思考是怎样试商的。

生1：把26看作30来试商。240里面有8个30，商8得208，余数是32，比除数大，说明商8小了，要调大，改商9，得到商9余6。

生2：我觉得也可以把26看作25来试商。4乘25是100，8乘25是200，余下的40里面还有1个25，所以商9。

师：生1用四舍五入法，把26看作30来试商，解决了问题，非常好！生2根据常用的4乘25等于100，把26看作25来试商，给出了解决问题的新思路。

生3：我还有一种方法，除数26不用估，直接思考10个26是260，比240多20，只要调整一下，就知道商是9。

师（指着被除数和除数的最高位）：你们明白生3的意思吗？

生4：我们之前研究过这个方法，被除数和除数最高位上的数相同，并且被除数的前两位比除数小，商是8或者9。

师：比较一下，哪种方法比较简便？为什么？

生5：我喜欢四舍五入法，一眼就能看出来。

生6：我觉得看作25更简便，因为我们常用4乘25等于100。

生7：我认为四舍五入法是最通用的，其他的方法要看具体情况。

师：其实，只要适合自己，又方便解决问题，就是最好的方法。

【设计意图：鼓励学生大胆发言，能增强学生灵活试商的意识和能力。通过对比，学生不仅进一步了解试商的过程，而且可以根据自己的情况选择合适的方法，提高试商能力。】

师：回顾一下，在计算除数是两位数的除法时是怎样试商的？

生8：一般是用四舍五入法，有时候也用其他方法。

生9：我补充一下，四舍五入法是最通用的方法，特殊情况要根据数的特点灵活试商。

师：是的，四舍五入法是最基本的试商方法，每个同学都要掌握。碰到特殊情况，具体问题具体分析，灵活运用，才能更好地解决問题。

【设计意图：反思学习过程，提炼学习方法，能促进学生在后续的学习中主动迁移，达到“教是为了不教”的目的。】

四、学以致用，固学练习

1. 我会纠错

[72）] [6 3 8][58）] [3 4 6][6 3 0] [8][70][60][3 4 8] [2]

2. 解决问题

（1）四、五年级共有612名学生，每18人组成一个环保小组，可以组成多少组？

（2）每节车厢限载31吨，要运走940吨货物，需要多少节车厢？

（3）服装店衣服每件29元，买2件49元，郑老师有185元，最多可以买多少件？

五、课堂小结，回顾过程（略）

【课后研思】

“除数是两位数的除法（试商）”是一节突破教材局囿的整合教学计算课，笔者进行如此大胆的教学尝试，是否得当尚待检验。但 “教无定法，贵在得法”，郑毓信教授指出：“数学核心素养的基本含义就在于：我们应当通过数学教学帮助学生学会思维，并能使他们逐步学会想得更清晰、更深入、更全面、更合理。”面对不同的试商方法，笔者组织和引导学生互说、互评、互学，在比较中求真，在应用中内化。其间，学生各抒己见，据理力争，思维频频碰撞，认定“到底哪种方法最好”已无太大价值，因为不同学生有着不同的认知水平和思维能力，经历对各种算法的再认识过程才是最有价值的，不但有利于促进学生优化思维，有利于激活学生自主探究的热情，也有利于增进学生学习数学的情趣，从而提高他们的数学运算能力。

当然，运算是解决问题的工具，只有在具体情境中才能真正认识到运算的作用。聚焦“试商”这一关键问题，创设常见的实际生活情境，不但让学生从数学的角度获取信息、提出问题，运用所学运算知识解决问题，还让运算不再是单纯的技能性训练，而是基于问题解决的需求，实现运算教学与解决问题的有效结合。如此，学生在整体试商中经历深度学习，提升思维品质，感受现实生活里蕴涵着丰富的数学信息，体会运算的价值和数学的应用，核心素养自然就会落地。

（责编 金 铃）