锥体锥角变化对旋风分离器性能的影响

李 杰，马 欣，王红霞，郑彦博

(1.黔南民族职业技术学院，贵州 都匀 55800，2.西南石油大学，四川 成都 610500)

0 引言

旋风分离器是一种无运动部件、结构简单、分离性能较好的重要净化设备。在水泥厂，石油天然气、页岩气以及煤炭发电等行业有着广泛的应用[1]。分离器内部流场极其复杂，已有很多的研究[11]。马欣等[4]分析研究了排气管外延长度对单级旋风分离器内部的速度流场，总压降值以及切割粒径的影响规律。Li等[5]创新改进排气管的结构来优化旋风分离器的分离性能，结果表明，通过在排气管深入段开孔，其最后的分离性能得到了相应的提高；李杰等[6]研究了排气管内置壁面厚度对旋风分离器性能的影响，得出结论，壁面厚度为0.1D时，分离性能较好；陈启东等[7]研究了圆柱段高度对旋风分离器性能的影响，结果表明，增加圆柱段高度，压降显著降低，分离效率提高。李琦等[8]研究了锥度对天然气净化用旋风分离器流场的影响，结果表明，在该实验组中锥度为172°时结构最优。并未研究锥角不变，延长锥体，对分离器性能的影响。本工作主要分析了锥角不变，筒体直径不变，延长锥体长度对旋风分离器流场及性能的影响，对旋风分离器结构设计方面具有研究意义。

1 计算模型和数值计算

1.1 结构尺寸及网格

旋风分离器几何结构及网格示意图如图1所示， bz代表标准的标准stairmand型[1]，具体的结构尺寸如表1：a组旋风分离器筒体直径保持不变，a1的筒体高度为h/2=150 mm，a2的筒体高度为a=100 mm，a3没有筒体高度，分离器全部用锥体；b组是保持锥体的锥度不变，b1的筒体高度为h/2=150 mm，b2的筒体高度为a=100 mm，b3没有筒体高度，分离器全部用锥体。旋风分离器bz、a1、a2、a3、b1、b2、b3的网格数依次为339818、339818、339818、339818、353160、346084、335664，网格质量均在0.6以上，能够确保仿真的准确性和可靠性。3个截面S1、S2、S3，如图1所示位置，分别为Z/D=2.25，2.75，3.75，其中，Z以旋风分离器的排尘口为起点。

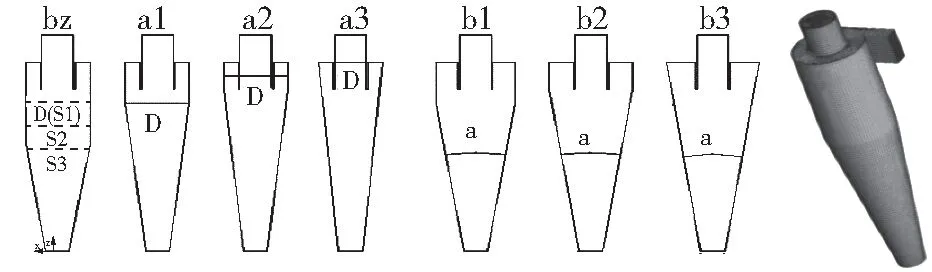
图1 旋风分离器几何结构图及网格示意图

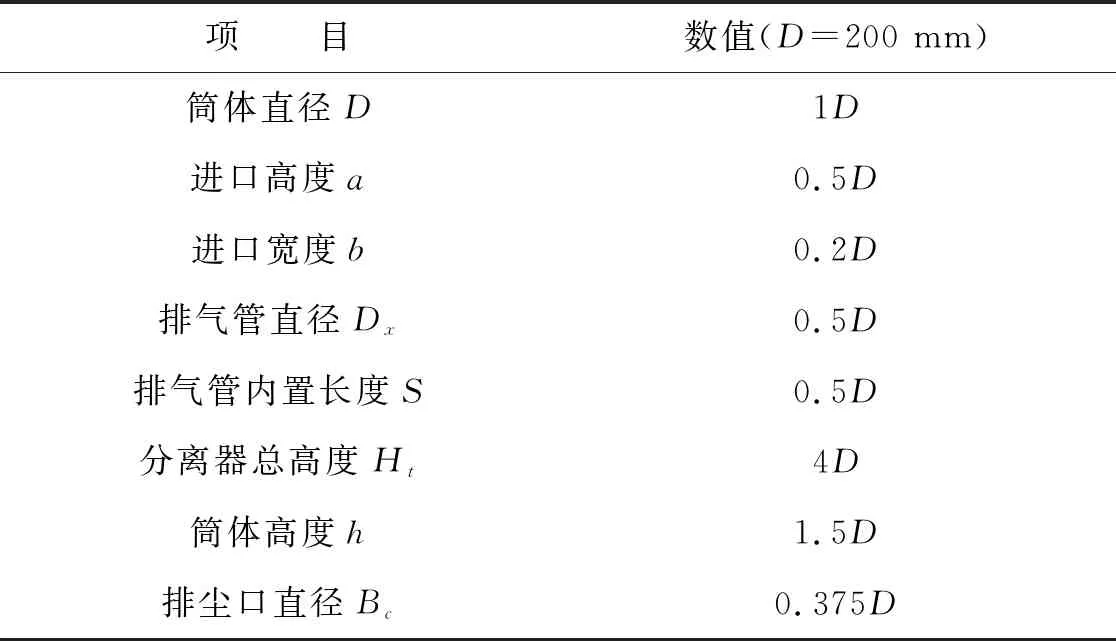
表1 旋风分离器的几何尺寸

1.2 计算模型

旋风分离器的气体相流域采用N-S方程和应力输运方程采用雷诺应力模型(RSM)求解，具体计算基本方程如下：

1)连续性方程：

(1)

2)动量方程：

(2)

3)雷诺应力模型输运方程

(3)

式中：扩散相，Di，j；应力产生项，Pi，j；浮力产生项，Gi，j；应力应变再分配项，Φi，j；离散相，εi，j；旋转系统产生项，Fi，j；r自定义源项，Suser；下标i，j，k为通用坐标方向[4]。

1.3 设置边界条件和选择数值解法

边界条件的设置与文献[9]的实验相同，气体相设置为常温常压空气，其物理化学属性保持默认。气体相空气和固体相颗粒的进口速度相同：V=15 m/s，固体相颗粒密度为ρ=2700 kg/m3，质量流量设置为0.001 kg/m3；排气管出口于气体相设置为outflow，于颗粒相设置为escape，排气口于颗粒相设置为trap，壁面边界保持默认reflect[6]。湍流强度I设置为4.7%，水力直径DH为57.2 mm。

对气体相，本文湍流模型选用雷诺应力模型(RSM)，压力与速度耦合选用SIMPLEC，离散格式选用QUICK，压力插补格式选用PRESTO；对颗粒相：采用DPM方法和随机轨道模型来处理[6]。以单相耦合计算，先进行8000步稳态求解，再进行步长为0.01，步数为400瞬态计算，得出收敛结果，进行分析。

2 数值模拟的可靠性验证

把数值模拟结果与实验结果进行对比分析，即把数值模拟旋风分离器内部流场的轴向速度和切向速度与实验的进行对比验证。Hoekstr等利用测速仪测量了旋风分离器内部流场的速度；本文数值模拟采用与文献[2]实验建立相同条件(几何尺寸，进口速度)，并与之进行对比。图2为距离排尘口942.5 mm处截面的无量纲切向速度与轴向速度的数值模拟结果与LDA实验测量值的对比。实验值与数值模拟的轴向速度、切向速度值基本吻合，该湍流模型和数值计算方法用来模拟旋风分离器的流场，其误差结果范围可接受[12]。

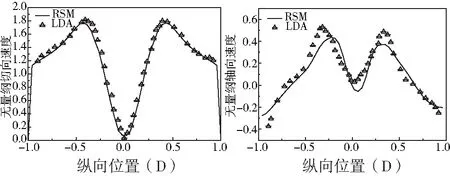
图2 旋风分离器数值模拟值与实验值对比结果

3 结果与分析

3.1 对旋风分离器流场的影响

3.1.1 切向速度分布

由图3旋风分离器的切向速度云图可看出，当筒体直径不变时，锥体段的长度逐渐减小，筒体段长度逐渐增大，最大切向速度先增大后减小，最大值为38 m/s；当锥体的角度不变化时，随锥体段长度逐渐增大，其最大切向速度也是先增大后减小。a1和a2的切向速度分布与标准stairmand型(bz)的切向速度分布最为相似，其中a3和b3在锥体段的涡核摆动幅度大，接近于排尘口的切向速度较大，会加剧粉尘颗粒对锥体壁面的磨损；b1和b2在排气管下口处的切向速度云图呈现喉结状。由图4切向速度曲线可以看出，a组旋风分离器在S1、S2、S3截面的切向速度总体都呈现a2>a1>bz>a3；b组旋风分离器在S1、S2、S3截面的切向速度总体都呈现b2>b1>bz>b3。通过把a组和b组与标准的stairmand型(bz)进行比较发现，锥体段延伸到旋风分离器入口高度或者说延伸到排气管内部高度相同时，旋风分离器内部流场的切向速度最大。从切向速度曲线看只有a3旋风分离器会出现中心切向速度为负，说明在中心位置存在二次涡流现象，且二次涡流对旋风分离器的分离效率会产生一定的负影响[4]。

3.1.2 轴向速度分布

由图3轴向速度云图可看出，几个模型的最大轴向速度值都出现在排气管内；标准型(bz)与a组分离器轴向速度最大值的大小关系为a2>a1>bz>a3，标准型与b组分离器轴向速度最大值的大小关系为b3>b2>b1>bz。由曲线图4的筒体截面S1可以看出，标准型与a组的筒体段轴向速度的大小关系为bz >a2>a1>a3，标准型与b组的筒体轴向速度的大小关系为bz >b2>b1>b3；从S2、S3截面曲线图可以看出，a组旋风分离器与标准型的锥体段轴向速度的大小关系为a2>a1>bz>a3，同样b组旋风分离器与标准型的锥体段轴向速度呈现b2>b1>bz>b3。呈现这种轴向速度关系的主要原因是由锥体段长度不同所导致的。

3.2 对旋风分离器压降的影响

从图5压降曲线图可看出，在a组和b组都是呈一个倒“V”形状，随锥体段的增长，筒体段的减短，其压降先增加后减小。从表2可看出，旋风分离器的压降最大值为a2和b2，以标准stairmand型为参考，压降值的最大值增大了34.5%，压降值的最小值降低了2.47%。产生a组和b组的压降值变化趋势的主要原因是由于锥体段的不断增加，其旋流与锥体段壁面碰撞摩擦阻力增加所导致。

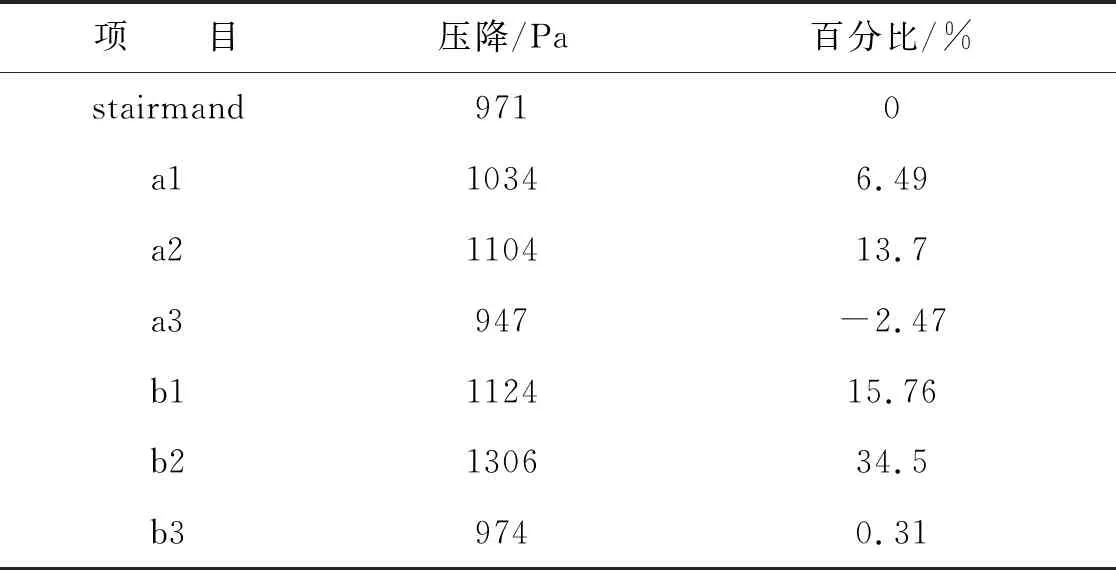
表2 bz、a组和b组旋风分离器的具体压降

图4 bz、a组和b组旋风分离器不同截面的切向速度和轴向速度图

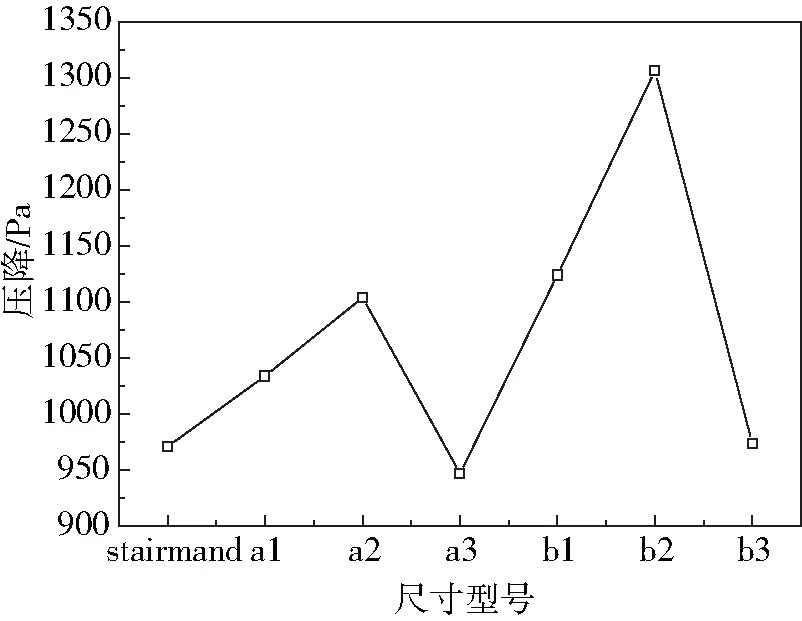
图5 bz、a组和b组旋风分离器压降曲线图

3.3 对旋风分离器分离性能的影响

用切割粒径来表征旋风分离器的分离效率，如图6和表3所示。由图6表3可看出，旋风分离器锥体的变化对其分离性效率有一定的影响，切割粒径随a组和b组的变化趋势几乎与压降变化趋势相反，呈“V”字形；随锥体段长度逐渐增大，筒体段长度逐渐减小，切割粒径先增大后减小；a2和b2旋风分离器的切割粒径在各组最小，对应其分离效率最高。在锥体变化后对旋风分离器的切割粒径除了b3外，其他模型的切割粒径都小于标准型，即分离效率高于标准型，其主要原因是a组和b组的切线速度基本都大于标准型。a2和b2的切割粒径为最小值，分别相对标准型分离器降低了5.97%、6.72%。综上所述，通过流场、切割粒径和压降对旋风分离器的性能研究，得出结论，筒体段长度等于标准型进口高度时，旋风分离器a2和b2的分离效率最高。

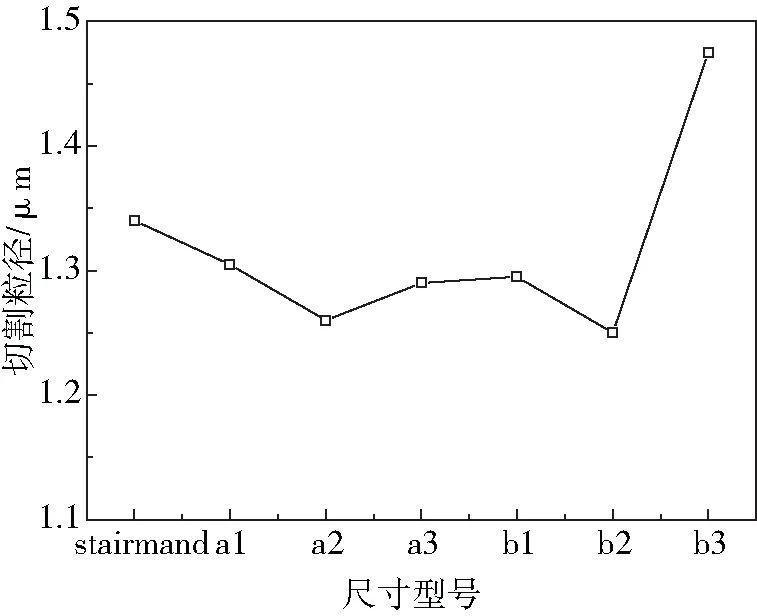
图6 bz、a组和b组的切割粒径的曲线图

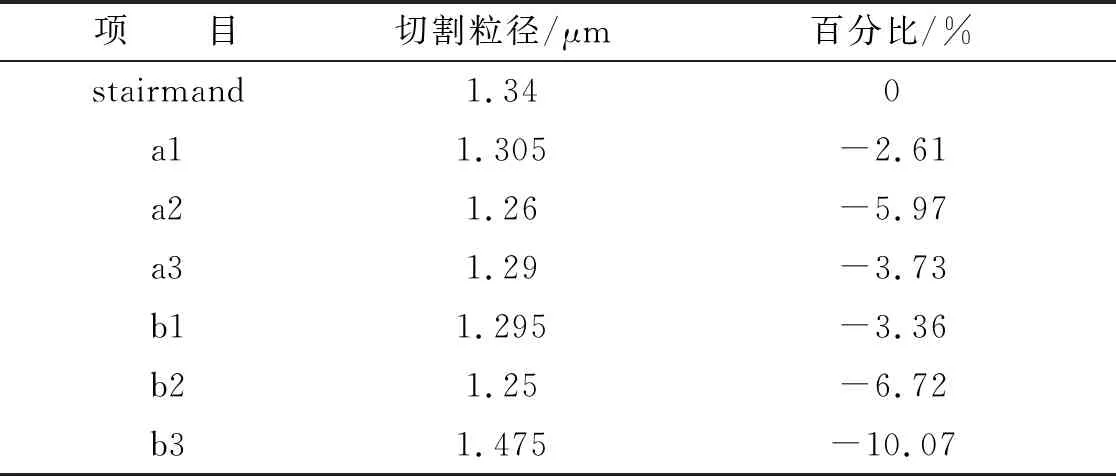
表3 bz、a组和b组的具体切割粒径

4 小结

为了优化标准stairmand型的结构，通过数值模拟分析，得出结论：

1)a2、b2分别在a、b组的切向速度最大，并大于标准型(bz)；a2、b2分别在a、b组的轴向速度最大，却小于bz型。a2和b2型的切向速度比标准型(bz)型大，即离心力大；轴向速度比标准型(bz)型小，即分离时间长，都有助于分离效率提高。

2)随锥体段长度增大，筒体段长度减小，a组和b组旋风分离器的切割粒径先增大后减小，变化趋势几乎与压降变化趋势相反，呈“V”字形，a2和b2旋风分离器的切割粒径在各组中最小，分离效率最高，分别相对标准型(bz)降低了5.97%、6.72%。即a2和b2型的分离效率高于标准型(bz)。

3)a组和b组旋风分离器随锥体段长度增大，筒体段长度减小，压降先增大后减小，变化趋势呈倒“V”形状。以标准型(bz)为参考，a2和b2旋风分离器的压降值为最大，分别相对标准型(bz)增大了13.7%、34.5%。即a2和b2型的压降高于标准型(bz)。工程上应根据分离效率和压降的综合分析，进行设计或选型。