双旋流耦合式旋流反应器内切向速度分布研究
2020-05-12
(1.中国石油大学(华东) 化学工程学院,山东青岛 266580;2.软控股份有限公司,山东青岛 266042;3.青岛市特种设备检验检测研究院,山东青岛 266101)
0 引言
在中国石油大学(北京)复合型离子液体催化碳四烷基化工艺[1-2]工业应用背景下,为了有效抑制副反应,提高烷基化油品质量,提出了一种双旋流耦合式旋流反应器[3]。张明阳等[4-6]对该双旋流耦合反应器的分离效率和轻相浓度分布开展试验和数值研究,确定了通过控制入口流量,可以调节反应器内轴向和切向旋转强度,实现耦合不同的旋流场来强化混合传质过程和两相快速分离的目的。但反应器内速度分布对混合与分离过程的影响并未见相关文献报道。双旋流耦合式旋流反应器为混合分离一体化设备,在强化轻、重两相液体接触混合传质的同时,还需要实现两相的实时分离。液液两相在旋流场下实现分离的前提条件,除了两相要有密度差,还需要在反应器内形成稳定的离心力场,而切向速度大小决定了反应器内离心力场强度及其分布情况。比如,若切向速度过大,虽然分散相越易破碎成小液滴进而提高两相接触混合,但分散相粒度越小则不利于两相的分离。由此可见,深入研究切向速度分布对明确双旋流耦合式旋流反应器内混合与分离过程耦合程度具有重要指导意义。
双旋流耦合式旋流反应器内流场极为复杂,很难通过试验手段准确测量其内流场及停留时间分布,而计算流体力学CFD[7-10]的飞速发展则为湍流场以及旋流反应器的研究提供了一种新的手段。王圆等[18]基于CFD技术,分析了4种不同单向入口油水分离器旋流器内压降特性。田洋阳等[19]利用FLUENT软件对两种导叶结构的旋流器内流场进行模拟,着重分析了旋流器内速度场、压力场以及剪切强弱。本文基于RSM湍流模型和欧拉多相流模型,对不同操作参数(流量、溢流比及进料比等)下的双旋流耦合式旋流反应器内切向速度分布开展数值研究,并建立旋流反应器内切向速度预测模型。
1 数值模拟及参数设定
1.1 旋流反应器几何模型及网格划分
双旋流耦合式旋流反应器结构如图1所示,具体结构尺寸见表1。

图1 旋流反应器结构示意

表1 旋流反应器结构尺寸 mm
重相离子液进入环形空间后,经导叶旋转加速,在柱段内壁面上形成具有一定厚度且高速旋转的液膜,轻相原料液从轻相入口管进入缓冲区,经切向开缝口进入旋流反应器柱段。由于原料液体密度较低,在下方切向入口进料后会在离心力的作用下向旋流反应器中心移动,这样必然会使轻相原料液穿过从上方入口进入的重相离子液体,轻重两相在径向上交错流动,强化两相之间的混合反应。之后,轻、重两相由于密度差在离心力场下实现快速分离,轻相从旋流反应器中心向上流动经溢流口管流出,重相则从底流口管排出,由此实现反应器内反应与分离一体化过程。网格划分如图2所示,轻相入口和导叶2个部分采用四面体网格,旋流反应器其它部采用六面体结构化网格。

图2 旋流反应器网格划分示意
1.2 数学模型
考虑到进入旋流反应器内的轻相液体占两相混合液总体积比大于10%,需要将颗粒群处理成在空间中各点性质具有连续性的拟连续介质,因此考虑两相流动的模拟选择欧拉多相流模型[11]。旋流反应器内流场呈现各向异性的强湍流特性,基于文献[12-13]中的模拟和试验结果,选择RSM湍流模型模拟旋流反应器内流场具有更高的精度。
1.3 初始条件及数值解法
本文模拟离子液体C4烷基化反应过程,考虑到甘油水溶液-煤油体系与离子液体-C4体系物理性质(详见表2)较为接近,本次冷态数值模拟及试验过程采用74wt%的甘油水溶液和煤油分别模拟离子液体和异丁烷。模拟中,轻相粒径设置为0.01 mm。旋流反应器轻相和重相的入口均设置成速度入口,速度大小、水力直径和湍流强度可由入口流量和入口截面积求得。将溢流口和底流口设置成自由出口,其中溢流口和底流口的出口流量权重则根据试验中不同的溢流比来设置(溢流比=溢流口流量/流入反应器总流量)。壁面边界设置为无滑移边界条件,粗糙度设置为0.5。本文旋流器反应器中的边界湍流将采用标准壁面函数进行处理。
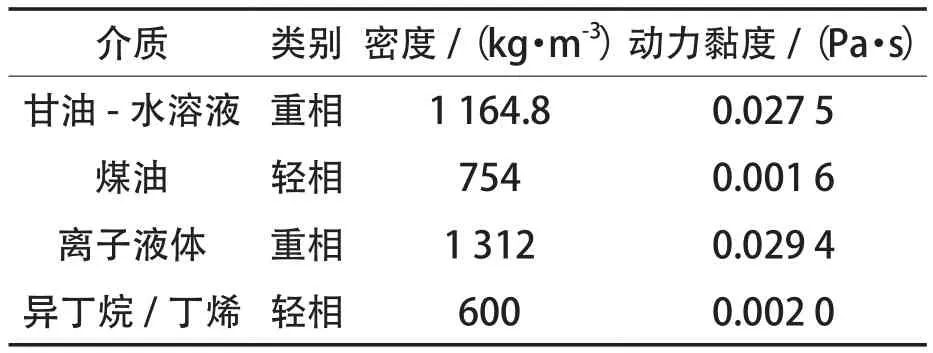
表2 20 ℃时各物质的物理性质
模拟计算采用有限体积法进行离散,其中时间离散和空间离散分别采用一阶隐式格式和QUICK差分格式,流动时均控制方程组的数值求解采用SIMPLE算法,压力插补格式则选用PRESTO!格式。
1.4 模型的验证
图3示出网格数量对数值模拟结果的影响曲线,可知轻、重两相回收率随着网格数量的增加基本保持不变,说明网格数量多少对计算结果影响可以忽略,为了在尽量短时间内取得数据,模拟时网格数量设置成30万。为了论证所采用的数学模型及计算方法的正确与合理性,将数值计算出的轻相含率与试验值进行对比,如图4所示。从图4可知由试验和模拟确定的旋流反应器轻相含率径向分布规律基本一致,其中心区域(r<0.005 m)轻相含率试验值和模拟值吻合较好,近边壁区试验值与模拟值相差较大,但误差范围在5%以内。考虑到靠近边壁区域为轻重两相混合接触区,两相流动较为复杂,导致试验测量误差增大,总体上看,不同进料比下的旋流反应器各截面上轻相含率试验结果和模拟结果变化趋势一致。由此可见采用RSM湍流模型和Eulerian多相流模型对该旋流反应器的两相流场进行模拟计算是合适的,模拟的结果能较为准确地反映旋流反应器内两相的流动情况。

图3 网格数量对轻、重相回收率的影响
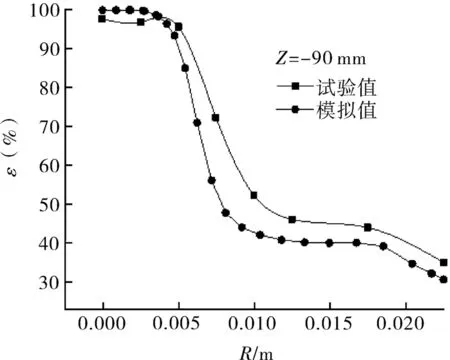
图4 轻相含率试验值与模拟值对比
2 模拟结果与讨论
2.1 切向速度分布
图5示出了旋流反应器不同轴向截面上轻相切向速度径向分布规律。由图可知,切向速度整体分布规律为:所有轴向截面呈中心对称分布;在壁面处切向速度为0。这与入口结构对称设置以及壁面效应相关。由图5还可知,在Z=-90 mm和Z=-115 mm两截面上,切向速度径向分布呈现“双峰值”分布,即从边壁向中心呈现先增大后减小,再增大又减小的趋势,切向速度最大值出现在r=-20 mm和r=-5 mm及对称的径向位置处;在2个切向速度峰值间存在一个切向速度减小区域,切向速度小离心强度降低,轻重两相不易分离,有利于两相的混合。说明在离轻重两相入口较近的区域(截面Z=-90 mm和Z=-115 mm)以轻重两相混合为主。随着轴向向下,与截面Z=-90 mm和Z=-115 mm不同,Z=-170 mm截面上轻相切向速度沿径向呈“单峰值”分布,即从边壁向中心呈先增大后减小的分布规律。而从截面Z=-210 mm到Z=-450 mm截面,切向速度径向分布规律基本相同,均呈现由边壁向中心先增大后减小的“单峰值”分布,呈现近似的水利旋流器Rankin涡结构[14-17]分布规律。说明从截面Z=-170 mm往下,旋流反应器内主要以分离为主。此外,沿轴向向下,基于能量守恒定律,由于流体和旋流反应器内壁面之间摩擦力的存在,消耗了进入旋流反应器流体的能量,切向速度峰值在减小,切向速度峰值所对应的径向位置也在逐渐向中心趋近。

图5 旋流反应器内轻相切向速度分布
2.2 入口总流量对切向速度的影响
图6示出不同入口总流量下旋流反应器内不同截面上轻相切向速度径向分布规律。在保持溢流比和进料比不变时,随着入口总流量的增大,所有位置切向速度增大,切向速度峰值也增大。这主要是因为入口总流量的增大,轻重两相入口流量增大,在旋流反应入口区形成的离心力增大,对应切向速度及峰值均增大。

图6 入口总流量对轻相切向速度分布的影响
需要注意的是在Z=-115 mm截面上,随着流量的增大,切向速度沿径向分布波动越大,“双峰值”分布更明显,更有利于两相的混合,而在Z=-450 mm截面上切向速度峰值所对应的径向位置基本不变,说明流量增加不太利于轻重两相分离。
2.3 溢流比对切向速度的影响
图7示出溢流比对旋流反应器不同轴向截面轻相切向速度分布规律的影响。
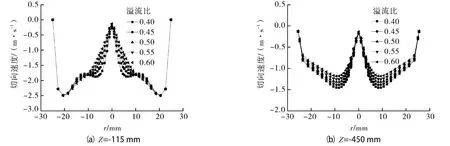
图7 溢流比对轻相切向速度分布的影响
在Z=-115 mm截面(混合段)上,随溢流比的增大,径向分布的对称性不变,但在-10 mm≤r≤0 mm(对应上行流)区域内切向速度逐渐减小,而在-20 mm≤r≤-10 mm内逐渐增大,对近边壁区的切向速度影响不大,且随着溢流比增大,切向速度由“双峰值”分布向“单峰值”分布靠近,说明溢流比增大,混合区内轻相液体也易向中心聚集,提高轻相回收率。在Z=-450mm截面(分离段)上,随着溢流比的增大,切向速度逐渐减小,但是出现切向速度最大值的位置没有变化,溢流比增大,从底流口流出的液体流量减小,对应的流速减小。
2.4 进料比对切向速度的影响
图8示出进料比对旋流反应器内轻相切向速度分布的影响。当保持入口总体积流量和溢流比不变时,增大进料比,即增大重相液体入口体积流量,由于重相液体经导向叶片旋转加速,进入旋流反应器内重相液体旋转及下行速度均随进料比增大而增大,而轻相液体在与重相液体接触后,随着重相液体作旋转下行运动,整体上来说,旋流反应器所有截面上切向速度随着进料比增大而增大;由8(a)可知,随着进料比增大混合段内径向速度逐渐形成“双峰值”分布,边壁区切向速度增大,但出现切向速度最大值的位置不变;由8(b)可知,进料比增大,切向速度最大值所在径向位置几乎不发生改变,仅切向速度值增大。

图8 进料比对轻相切向速度分布的影响
2.5 切向速度模型的建立
2.5.1 最大切向速度位置
最大切向速度是切向速度的一个重要特征量,其位置连线形成一条最大切向速度轨迹面,不少学者以此作为分离界面。在轴流式和切流式旋流器内,认为rm=2ro/3(ro为溢流口内半径),从图9可知,在本文的双旋流耦合式反应分离一体化反应器内rm≠2ro/3,且操作参数(入口流量、溢流比、进料比等)对最大切向速度位置影响很小,可以忽略。则由图9知,在混合段内随着轴向向下rm线性减小。

式中 rm——最大切向速度位置,mm。
在分离段,最大切向速度位置随轴向位置的变化关系如下:
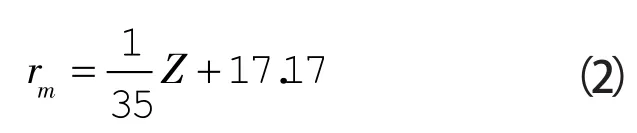
本旋流反应器锥段角度的正切值也等于35,由图也可看出不同轴向位置处最大切向速度位置连线与旋流反应器锥体平行,因此,分离段内的rm与Z的关系可以写成:
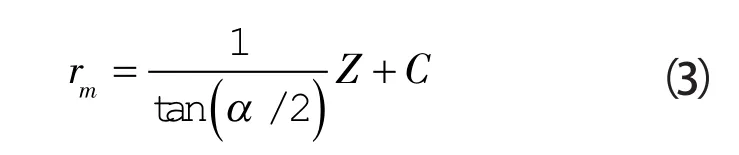
当F=0.4,Z=-450 mm时,分别求出rm=4.31 mm小于零速半径rLo=5.23 mm。即最大切向速度轨迹面处于上行流区域内,处于此面的液相早已被分离,因此不可以将最大切向速度轨迹面作为本旋流反应器的分离界面。
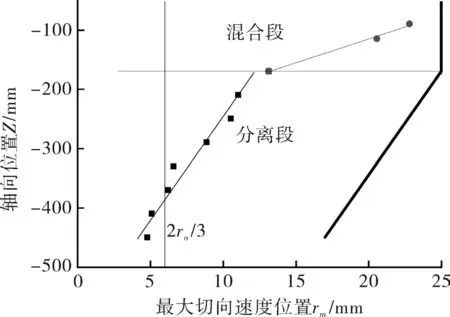
图9 rm随Z变化曲线
2.5.2 切向速度模型
由前面的分析还知道,在混合段内切向、轴向速度分布较为复杂,不便于用方程进行拟合。本节重点分析对分离起主要作用的锥段,对其各截面处的速度分步进行拟合,选取流量为4 m3/h,进料比为1,溢流比为0.4的数值模拟数据进行拟合。
由2.1节分析可知,切向速度存在最大值,以最大值为分界点,分为内旋流区和外旋流区,切向速度在两个流动区内变化规律不同,因此,对内外旋流区分别采用不同拟合函数关系进行拟合。
(1)内旋流区切向速度
根据数值模拟数据拟合,该区内速度分布满足幂指数关系,即:

式中 ut——切向速度,m/s;
C1——轴向位置的函数;
r ——测点半径,m;
R ——旋流反应器柱段半径,m;
n ——幂指数。
根据上式计算得到内旋流区n和C1的值见表3。

表3 内旋流区切向速度拟合函数系数
由 表 4 可 知,i,n值 范 围 为 0.5~0.6,C1值为-10~-14,且两者与轴向位置均成线性关系n=0.000 1Z+0.635 3,C1=0.012 6Z-8.311。
(2)外旋流区切向速度
根据数值模拟数据拟合,该区内速度分布满足线性关系,即:

式中 C2,C3——常数。
不同轴向位置处C2和C3的值见表4。

表4 外旋流区切向速度拟合函数系数
C2和C3均与轴向位置均成线性关系,C2=-0.002 8Z+3.177,C3=-0.009 7Z-9.733。将上述结果总结后得到切向速度总表达式:
式(6)的计算结果与实测值的比较如图10所示,可以看到本切向速度计算模型的准确度比较高。


图10 切向速度计算值与模拟值比较
3 结论
(1)旋流反应器混合段:切向速度沿径向呈“双峰值”分布,有利于轻重两相混合接触,促进相间传质。
(2)旋流反应器分离段:切向速度呈 “单峰值”分布,以最大切向速度为界,分为内旋流和外旋流区,说明该反应器可以实现实时分离。
(3)入口总流量增大时,混合段内切向速度径向波动增大,但分离段内最大切向速度位置不变,说明流量的增大有利于液液两相混合,但不利于两相分离。
(4)溢流比增大,混合段内切向速度由“双峰值”分布向“单峰值”分布靠近;分离段内,切向速度略有减小;说明溢流比增大有利于提高轻相回收率,不利于两相的混合。
(5)建立了切向速度预测模型,与试验值较吻合,计算模型的准确度比较高。
