TBM开挖深埋铁路隧道引起的围岩扰动分析

王飞阳，周凯歌，方 勇，徐公允，汪辉武，卓 彬

(1. 西南交通大学 交通隧道工程教育部重点实验室，四川 成都 610031；2. 中铁二院工程集团有限责任公司，四川 成都 610031)

0 引言

我国铁路隧道正朝着长距离、大埋深方向发展，伴随着施工机械化水平的提高，TBM逐渐应用于隧道建设中[1]。深埋隧道地应力水平高，应力场复杂多变。众多学者对TBM深埋隧道掘进过程中可能遇到的工程问题进行了研究。如: 钱七虎等[2]分析了TBM在深埋隧道掘进中可能出现的工程难点及发展前景； 荆留杰等[3]阐述了TBM施工中可能遇到的地质灾害及其处理措施。TBM在深埋隧道中掘进时可能会出现岩爆、卡机等灾害，而要减少此类工程问题产生的危害，需要对掘进过程中围岩的稳定性进行研究。冷先伦等[4]采用FLAC 3D建立数值模型，针对不同TBM掘进速率下的隧道围岩扰动区进行了研究； 赵红亮等[5]通过数值分析的方法，对深埋洞室开挖过程中岩体的应力变化特征进行了研究； 吴文平等[6]依托实际工程，分析了围岩的破坏特征及防治措施； 刘凯等[7]采用FLAC 3D对大伙房引水隧洞进行了掘进模拟，分析了TBM隧道开挖过程中围岩的变形； 唐彬等[8]采用Abaqus模拟了TBM巷道施工过程，基于围岩应力分布及变形特点分析了TBM巷道围岩的稳定性。对于深埋硬岩隧道，相比于钻爆法，由于TBM开挖过程是准静态卸荷过程，TBM掘进对围岩的扰动更小、更容易积聚弹性应变能[9]。然而，现有研究多集中于围岩应力重分布的特征上，对TBM隧道掘进过程中弹性应变能的分布特征研究较少，而弹性应变能的分布与硬岩隧道的岩爆发生息息相关。

鉴于此，本文依托实际铁路隧道工程，采用FLAC 3D数值模拟软件，建立TBM隧道掘进模型，对TBM掘进过程中的应力分布特征进行分析，并基于力流理论解释应力集中的原因，最后结合弹性应变能理论对TBM隧道最有可能发生岩爆的位置进行预测。

1 工程概况

某铁路隧道拟采用双护盾TBM施工，该隧道最大埋深约1 480 m，隧道半径为5.2 m，岩层以花岗岩为主，隧道构造应力显著，易产生岩爆。水压致裂地应力测试结果表明，在测量深度范围内主应力随地层深度的增加而增加，最大水平主应力随测试深度增加的幅度大于垂直主应力，最小水平主应力增加速度最小。区域应力场受构造影响较大，水平主应力占优势，为σhmax>σv>σhmin构造型应力场。拟合主应力随深度变化的公式为：

σhmax=0.027H-2.400 0；

(1)

σhmin=0.015 7H+0.618 7；

(2)

σv=0.019 3H-0.090 0。

(3)

式(1)—(3)中：σhmax为最大水平主应力，MPa；σhmin为最小水平主应力，MPa；σv为垂直主应力，MPa；H为隧道埋深，m。

2 数值模拟

2.1 初始模型

为了削弱模型边界的影响，模型边界考虑圣维南原理，隧道边界取3～5倍洞径为宜[10]。模型宽度取120 m、高度取120 m、长度取60 m。为了提高计算精度，将隧道及隧道附近围岩的网格适当加密。FLAC 3D数值计算模型如图1所示。

图1 数值计算模型(单位： m)

郭延辉等[11]通过采用FLAC 3D数值模拟软件对不同边界条件进行模拟试验后发现，位移边界条件、应力边界条件及混合边界条件均不能满足初始水平构造应力场的模拟要求，而基于初始应变能理论的效果较好。在采用位移边界条件的情况下，将模型所有单元应力初始化。模拟埋深为1 000 m，根据式(1)—(3)计算得到洞身附近σhmax为24.60 MPa、σhmin为16.32 MPa、σv为19.21 MPa，为σhmax>σv>σhmin构造型应力场。模型底面采用固定边界，侧面采用位移边界条件，初始地应力通过initialize命令赋予模型。将围岩视作均质、各向同性的弹塑性材料，材料采用摩尔-库仑屈服准则。根据工程地质勘察资料，隧道围岩物理力学参数如表1所示。

表1 隧道围岩物理力学参数

2.2 TBM模拟

TBM在实际开挖中，隧道开挖中心线、刀盘回转中心线、护盾中心线不在同一直线上，围岩与护盾之间的间隙为上大下小的偏心分布。依据双护盾TBM自身的结构构造以及围岩与护盾之间间隙的偏心分布，对TBM的主要部件进行模拟，主要部件尺寸如表2所示，双护盾TBM模拟及细部构造如图2和图3所示。模型中刀头、护盾、管片及盾尾注浆采用弹性模型。通过改变盾尾注浆材料的弹性模量来模拟注浆材料的不同阶段，注浆前1 m为软质阶段，其余为凝固硬化阶段。管片、刀头、护盾及盾尾注浆等材料物理参数见表3。

表2 双护盾TBM主要部件尺寸

图2 双护盾TBM模拟

图3 双护盾TBM细部构造

表3 双护盾TBM材料物理参数

刀头、护盾及盾尾注浆与围岩的相互作用通过建立接触面来模拟。TBM掘进施工中，安装在TBM刀盘上的盘形滚刀在推力和滚动力的共同作用下滚压掌子面，使掌子面处岩石产生裂纹并破碎，以达到破岩开挖隧道的目的[12-13]。通过对掌子面单元节点同时施加法向力及切向力来模拟刀盘对掌子面的推力及滚动力，从而实现TBM掘进过程中刀盘对掌子面的滚压作用。

TBM掘进施工中，机身质量作用在隧道底部围岩上，对底部围岩的应力释放有一定的抑制作用，因此，TBM机身质量在数值模拟中不可忽视。机身质量的模拟是通过法向力的方式施加在隧道底部1/4圆周上[14]。

2.3 TBM连续掘进模拟

对TBM连续掘进施工过程进行模拟，每次开挖向前掘进1 m。TBM掘进施工步骤如图4所示。掘进施工步骤为： 1)施加初始应力初始化模型； 2)刀盘进洞； 3)前盾进洞，在围岩与护盾之间建立接触面，每步开挖进尺为1 m，同时在掌子面上施加法向力及切向力； 4)后盾进洞，与前盾模拟方法一致； 5)激活管片及注浆回填； 6)注浆回填材料凝固硬化。

(a) 模型初始化 (b) 刀盘进洞

(c) 前盾进洞 (d) 后盾进洞

(e) 注浆未硬化阶段 (f) 注浆凝固硬化阶段

在FLAC 3D数值模型中，通常将隧道模型沿掘进方向划分成若干个小的开挖步，然后逐步对每个开挖步赋予null模型实现隧道的开挖。然而，TBM掘进开挖是一个连续的过程，如果每2个开挖步之间计算至平衡，即使将模型的网格尺寸划分得足够小，也无法有效地模拟TBM开挖过程的连续性，而且会消耗太多的时间步。为了更真实有效地模拟TBM连续开挖过程，采用逐步释放不平衡力的方法，并以0.875作为应力释放系数[15]。具体做法为： 考虑模型计算时间步的消耗，将沿隧道开挖方向的网格进行适当加密；每个开挖循环完成后，计算1步； 提取当前开挖步周边单元节点上的不平衡力，乘以1与应力释放系数0.875的差值； 将所得到的数值以反向荷载的形式施加于开挖步周边单元节点上，计算至平衡。

3 数值模拟结果

3.1 应力分布

在拱顶、拱肩、拱腰、拱脚和拱底处分别设置监测点，监测断面Y方向坐标为30 m。测点分布如图5所示。

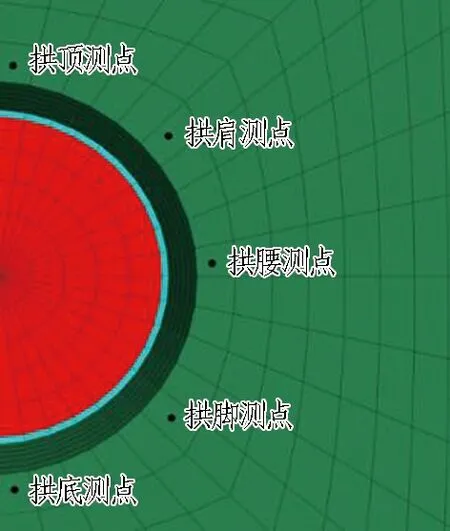
图5 测点分布

初始地应力状态下，地层区域应力场受地质构造影响较大，水平主应力占优势，隧道洞身附近最大主应力方向为横向(x)，中间主应力方向为竖向(z)，最小主应力方向为掘进方向(y)。为了明确TBM掘进施工中的围岩应力分布特征，研究了各测点最大主应力σ1、中间主应力σ2、最小主应力σ3、竖向应力σz、掘进方向应力σy以及横向应力σx随掌子面推进距离的变化规律，如图6所示。

由图6(a)可知： 当掌子面距离监测断面较远时，σ1、σ2和σ3分别与σx、σz和σy的变化趋势一致且数值相近，说明此时TBM开挖对监测断面处围岩的扰动极小，围岩应力状态与初始地应力状态基本一致； 当掌子面在监测断面前方10 m左右(约1倍洞径)时，应力变化明显，σ1依然和σx数值相近且变化规律一致，但此时σ2与σy以及σ3与σz变化规律一致； 当掌子面通过监测断面且围岩应力趋于稳定后，σ1、σ2和σ3分别与σx、σy和σz数值接近； 由于各主应力间方向两两垂直，且σx、σy和σz方向两两垂直，说明在TBM开挖后，σ1的方向大致为横向，σ2的方向由竖向转变为掘进方向，σ3的方向由掘进方向转变为竖向； 当所有应力趋于稳定后，σ1表现出明显的应力集中，σ2、σ3则表现出一定的卸荷特性，其中σ1、σ2和σ3分别为初始地应力状态的1.78倍、1.07倍和0.43倍。由图6(e)可知，拱底各应力变化规律与拱顶基本一致，拱底各应力趋于稳定后，σ1、σ2和σ3分别为初始地应力状态的1.80倍、1.06倍和0.43倍。

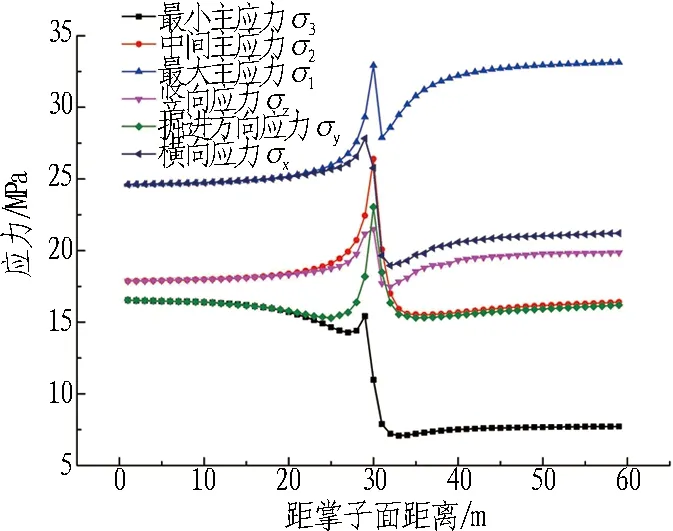
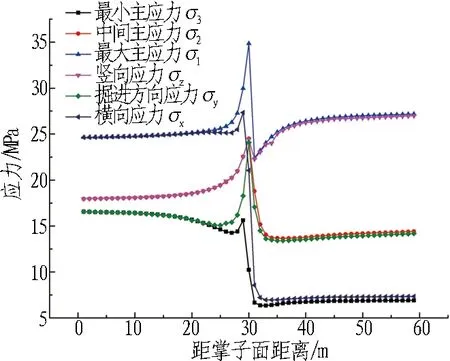
(a) 拱顶 (b) 拱肩 (c) 拱腰

由图6(b)和图6(d)可知： 当掌子面通过监测断面时，只有σ2与σy的变化趋势一致，且σx总体上呈下降趋势，当各应力趋于稳定后，只有σ2与σy数值接近，此时σ1与σx或σz，σ3与σx或σz应力数值并不接近，σ2与σy虽然数值接近，但两者方向不一定一致； 当拱肩、拱脚各应力趋于稳定后，拱肩处σ1、σ2和σ3分别为初始地应力状态的1.35倍、0.92倍和0.47倍，拱脚处σ1、σ2和σ3分别为初始地应力状态的1.46倍、0.95倍和0.47倍。

由6(c)可知，当拱腰各应力趋于稳定后，σ1、σ2、σ3分别与σz、σy、σx数值相近，说明此时σ1的方向大致为竖向，σ2的方向大致为掘进方向，σ3的方向大致为横向，σ1、σ2和σ3分别为初始地应力状态的1.10倍、0.80倍和0.42倍。

由以上分析可知，TBM开挖过程中会对掌子面前方10 m左右(约1倍洞径)的围岩应力造成显著影响，在开挖完成向前推进10 m左右时，各应力趋于稳定水平。TBM开挖后，各测点的σ2和σ3均表现出一定的卸荷特征，除拱腰外，其余测点的σ1均表现出明显的应力集中，其中拱顶和拱底最为明显。TBM开挖过程中，随着掌子面的推进，拱顶和拱底各应力变化规律基本一致，拱肩和拱脚各应力变化规律基本一致，TBM隧道围岩应力大致呈上下对称分布，TBM的质量对隧道围岩应力的分布影响很小。

3.2 应力集中力流解释

为分析TBM隧道掘进过程中应力集中的原因，采用机械工程中统一强度理论的结构力流优化分析方法(即力流法)。力流法用于分析受力系统中力的传递，将力的传递拟作水的流动，用力线表示力流路径，力线的疏密反映应力的大小[16]。

初始地应力状态下，隧道洞身附近最大主应力方向为横向，中间主应力方向为竖向，可将隧道附近围岩视为其余岩体作用下的受力系统。依据力流的特点(力流传递遵循路径最短原则，力流转向遵循平缓原则)，绘制隧道力流路径图，如图7所示。

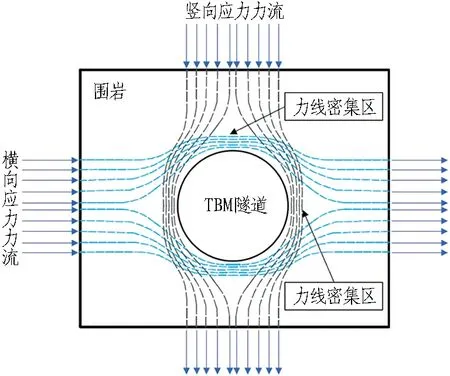
图7 隧道力流路径图

由图7可知，隧道开挖后竖向应力力流主要在拱腰处形成力线密集区，横向应力力流主要在拱顶及拱底处形成力线密集区。由此可知： 在拱顶及拱底处，由于开挖卸荷，横向应力会产生显著的应力集中现象，致使σ1数值与σx相近； 竖向应力在拱顶及拱底处表现出应力分散的特性，使得拱顶竖向应力显著下降，致使σ3数值与σz相近； 由于各主应力间方向两两垂直，开挖完成后，致使拱顶及拱底处σ2数值与σy相近，且σ1、σ2、σ3的大致方向分别为横向(x)、掘进方向(y)、竖向(z)。同理，拱腰处由于横向应力力流的转向，使得σx大幅下降，从而致使σ3与σx方向基本一致，数值相近；σz在拱腰处产生应力集中，使得拱腰处σz增大，从而致使σ1与σz方向基本一致，数值相近，σ2与σy方向基本一致，数值相近。当拱腰处所有应力趋于稳定后，σ2、σ3呈现出一定的卸荷特征，σ1表现出一定的应力集中，但不明显，说明横向应力的重分布对σ1的应力集中程度影响显著。

由图6(b)和图6(d)可知，TBM开挖后，拱肩与拱脚处横向应力和竖向应力均不会产生应力集中，且横向应力大幅下降，而拱肩与拱脚的最大主应力却依然表现出显著的应力集中现象，主要原因可能是在这种力流路径下造成拱肩与拱脚处的径向剪应力增大。图8为隧道开挖后围岩径向剪应力云图。

图8 隧道开挖后围岩径向剪应力云图(单位： Pa)

由图8可知，剪应力主要在拱肩和拱脚处产生应力集中，且在数值上呈上下对称分布，拱顶、拱底和拱腰处剪应力极小。由此说明，拱肩与拱脚处σ1应力集中主要是由于剪应力大幅增加造成的，而拱顶、拱底与拱腰处σ1应力集中主要是由于正应力大幅增加造成的，这与上述拱顶、拱底与拱腰的应力分析结果一致。

由以上分析可知，在TBM隧道中，力流路径对应力分布影响显著，拱顶和拱底、拱肩和拱脚、拱腰处σ1应力集中分别主要来自横向应力、剪应力和竖向应力，在水平应力构造显著的情况下，σx的重分布对σ1的应力集中程度影响显著。

3.3 弹性应变能结果分析

隧道开挖后，由于开挖卸荷，岩石会释放部分弹性应变能，但是开挖后应力的重分布反而可能造成部分岩体弹性应变能的积聚，当弹性应变能积聚到一定程度时极有可能发生岩爆。由此，要分析隧道开挖后围岩的稳定性，有必要对隧道开挖后弹性应变能的重新分布进行研究。

弹性应变能可用3个主应力表示，为

σ2σ3)]。

(4)

式中：Ue为弹性应变能，kJ/m3；E为弹性模量，MPa；σ1、σ2和σ3为围岩的3个主应力，MPa；ν为泊松比。

计算过程中，基于FLAC 3D内置的fish语言，依据式(4)对各测点的弹性应变能进行监测，并绘制各测点主应力与弹性应变能变化曲线，如图9所示。

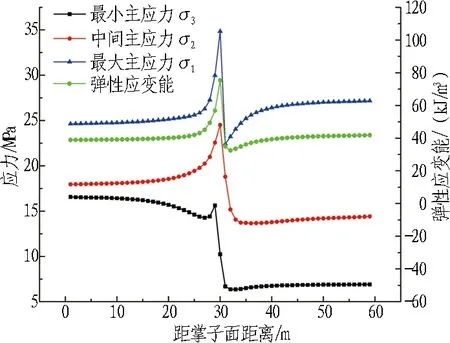
(a) 拱顶 (b) 拱肩 (c) 拱腰

由图9可知： 各测点弹性应变能均在距监测断面10 m左右时开始跃升，且随着掌子面的推进，增长幅度越来越大，在掌子面到达监测断面时，各测点弹性应变能均达到最大； 当掌子面推过监测断面时，各测点弹性应变能在出现突然的大幅度跌落后继续增长，但增长幅度越来越小； 当掌子面推过监测断面10 m左右时，各测点弹性应变能趋于稳定。各测点的弹性应变能均较开挖前高，其中拱底和拱顶弹性应变能增长幅度最大，分别为开挖前的2.842倍和2.807倍； 拱脚和拱肩其次，分别为开挖前的1.859倍和1.592倍； 拱腰最小，为开挖前的1.075倍。

文献[17-18]的研究认为花岗岩等硬质岩弹性应变能大于40 kJ/m3时即有可能发生岩爆，弹性应变能大于100 kJ/m3时发生岩爆的可能性较大。隧道穿越岩层以花岗岩为主，TBM开挖后，拱肩和拱脚的弹性应变能大于40 kJ/m3，有发生岩爆的风险； 拱顶和拱底的弹性应变能大于100 kJ/m3，发生岩爆的可能性较大； 拱腰处的弹性应变能水平较低，发生岩爆的风险较小。由此可知，在穿越岩层以花岗岩为主的TBM隧道中，最有可能发生岩爆的位置为拱底和拱顶，其次为拱脚和拱肩。

由图9分析可知，TBM隧道中各测点弹性应变能变化趋势与σ1变化趋势一致，σ2及σ3对弹性应变能的变化规律影响不明显，且围岩弹性应变能大致呈上下对称分布，与应力的重分布规律一致，说明TBM隧道开挖中围岩弹性应变能跃升主要是由于σ1应力集中引起的。由TBM隧道围岩应力分析可知，横向应力的重分布对最大主应力的应力集中程度影响显著，σ1应力集中程度从大到小依次为拱底、拱顶、拱脚、拱肩和拱腰。由以上分析可知，弹性应变能跃升水平依次为拱底、拱顶、拱脚、拱肩和拱腰，与应力集中程度排序一致。由此分析可知，TBM在横向应力显著的水平构造型应力场中开挖时，横向应力的重分布通过影响σ1的应力集中程度从而使围岩弹性应变能跃升。横向应力重分布是TBM隧道围岩弹性应变能积聚的主要原因，σ1的应力集中程度反映了弹性应变能的跃升水平。

4 结论与讨论

依托实际铁路隧道工程，采用FLAC 3D数值模拟软件建立TBM隧道掘进模型，对隧道围岩应力分布特征进行分析，并基于力流理论解释了应力集中的原因，最后结合弹性应变能理论对隧道岩爆位置进行预测，得到以下结论。

1)TBM开挖过程中会对掌子面前方10 m左右(约1倍洞径)的围岩应力及弹性应变能造成显著影响，在开挖完成向前推进10 m左右时，各应力及弹性应变能趋于稳定。

2)TBM隧道开挖过程中，围岩应力及弹性应变能变化规律大致呈上下对称分布，TBM的质量对围岩应力重分布影响极小。

3)在横向应力显著的水平构造型应力场中，横向应力的重分布对最大主应力的应力集中程度影响显著，拱顶和拱底、拱肩和拱脚、拱腰处最大主应力集中分别主要是由横向应力、剪应力、竖向应力集中引起的。

4)TBM隧道开挖过程中围岩弹性应变能跃升主要是由于σ1应力集中引起的，σ1的应力集中程度反映了弹性应变能的跃升水平。在穿越岩层以花岗岩为主的TBM硬岩隧道中，拱顶和拱底的应力集中程度最大，弹性应变能跃升水平最高，发生岩爆的可能性最大，其次为拱肩和拱脚，拱腰处弹性应变能水平较低，发生岩爆的风险较小。

5)机械工程中统一强度理论的结构力流优化分析方法可以用于解释隧道开挖应力重分布的产生机制，可为此类研究工作提供参考。

本文仅研究了隧道沿与最大主应力方向垂直开挖时引起的围岩扰动，然而许多隧道的最大主应力方向可能与隧道掘进方向一致，也可能与隧道轴线方向存在一定夹角，因此，不同应力场下围岩的扰动尚需研究。此外，本文仅以弹性应变能大小为指标预测了岩爆的发生位置，而岩爆的发生与诸多因素有关，国内外学者也建立了许多关于岩爆的判据，下一步的研究应当考虑从不同的判据预测岩爆的发生位置。