单跨5车道公路隧道过渡“3+2”小净距隧道施工力学研究

2021-03-15张俊儒王智勇龚彦峰徐向东

隧道建设(中英文) 2021年2期

张俊儒，王智勇，龚彦峰，徐向东，张航，叶伦

(1. 西南交通大学交通隧道工程教育部重点实验室，四川成都 610031；2. 中铁第四勘察设计院集团有限公司，湖北武汉 430063)

0 引言

城市地下交通具有不受地面机动车、行人和天气的干扰，车辆通行效率高等优点，已成为当今城市地下空间开发利用的主要形式之一[1-2]，而地下互通式立交则是担任连接地下交通网络的重要节点。城市互通地下立交可以分为平面交叉段和立体交叉段2部分。平面交叉段即分岔隧道，通常由大跨段、连拱段、小净距段以及分离段组成[3]，主要特点是开挖面积大、扁平率低，因此优先考虑CD法、台阶法、双侧壁导坑法等分部开挖方法来减小围岩的扰动，这决定了分岔隧道施工力学机制的复杂性。与一般分岔隧道不同的是，厦门芦澳路—海沧疏港通道地下互通立交隧道由单洞5车道隧道直接过渡至“3+2”小净距隧道(主洞3车道和匝道2车道)，没有设置连拱隧道过渡，这在国内地下立交分岔隧道的修建中较为少见。分岔隧道由大跨段直接过渡到小净距段，是施工过程中非常复杂的工序转化，施工力学机制难以把控，加之现在没有相应的施工和设计规范，也没有成熟的现场施工经验，现场采用支护手段和施工方法往往趋于保守，施工效率受到很大的影响。

国内诸多学者对超大断面分岔隧道进行了研究。张俊儒等[4]对中国4车道及以上超大断面公路隧道修建技术的发展进行归纳总结，大断面分岔隧道多是由多种断面分段扩大的方法进行过渡，且施工工法多为分部施工工法。蔚立元等[5]采用数值模拟结合模型试验的研究手段，对八字岭分岔隧道的大跨段至连拱段、连拱段至小净距段2个过渡段进行研究，研究表明拱顶、中隔墙和夹岩等受隧道开挖影响较大；第2个过渡段的拱顶位移、主应力均比第1个过渡段大。周峰等[6]则通过现场监控量测发现八字岭分岔隧道的大跨段稳定性好，锚杆受力小，连拱段锚杆受力较小，但受地质条件影响较为明显，小净距段锚杆受力最大但仍小于容许应力。阙坤生[7]通过数值模拟的方法发现，在小净距隧道施工时，先行隧道对后行隧道的影响小于后行隧道对先行隧道的影响；小净距隧道施工时彼此远离一侧的隧道结构应先施工，以避免隧道受力偏压。王汉鹏等[8]建立了弹塑性损伤耦合模型，分析了八字岭分岔偏压隧道在不同施工顺序下分岔隧道围岩位移、应力和损伤区，发现左洞(埋深较大一侧)超前右洞32 m以上，才能减弱左右洞施工相互影响；从围岩损伤区来看，靠近连拱段的小净距隧道中夹岩柱为最危险区域，施工时应给予重视。闫自海等[9]以杭州市紫之隧道的地下立交交叉口工程为依托，提出一种“小洞开大洞，先横向开挖再反向开挖”的施工工法，并用有限元模拟及现场监控量测的方法验证了该施工工法的合理性。林志等[10]以重庆两江隧道工程为依托，建立了大型江底地下互通式立交平交段的设计与施工方法。刘鹏[11]以胶州湾隧道工程为研究对象，通过工程类比以及数值分析的方法确定了小净距隧道段的范围，并提出了相应的施工工法及支护措施，实现了该浅埋分岔隧道的快速施工。朱道建[12]对喇叭口分岔隧道进行计算分析，提出了由大跨隧道过渡至连拱隧道进而转换至小净距隧道的步骤。

通过以上调研可以发现各个工程特点不同，研究人员的研究重点也不相同。超大断面隧道围岩应力状态复杂，当前还没有统一的支护和设计规范[13]，也始终未能形成统一且有说服力的理论；而且全分岔隧道围岩应力受隧道净距和断面形式的影响，分岔隧道的施工与支护结构设计面临诸多难题。本文所依托的芦澳路—疏港通道地下互通立交工程为单跨5车道直接过渡“3+2”小净距隧道工程，由大跨隧道直接过渡到小净距隧道的施工力学十分复杂。通过对大跨段与小净距段交界处以及小净距隧道的施工力学进行研究，得到分岔隧道大跨段直接过渡至小净距段的施工力学特征及规律，在此基础上提出相应的施工对策。

1 工程概况

1.1 工程背景

厦门芦澳路—疏港通道地下互通立交隧道位于厦门市海沧区。芦澳路工程路线呈南北走向，起点接芦澳路跨南海三路跨线桥，路线往北穿越蔡尖尾山后，与疏港通道相交处设置A、B、C、D匝道隧道形成地下互通立交，如图 1所示。疏港通道2#隧道左线长4 240 m，右线长4 250 m。超大扁平5车道分岔隧道位于疏港通道2#隧道，起讫里程为YK2+343～+622.5。

1.2 工程水文地质条件

疏港通道2#隧道主要穿越花岗岩地层，进出口段地表分布第四系残坡积层，隧址区构造发育，位于大帽山—石峰岩断裂带，处于石峰岩断块上。在多期构造应力作用下，岩体节理、裂隙较发育，岩体较完整—破碎。分岔隧道通过燕山晚期第2次侵入花岗岩地层(γ53(1)b)，中粗粒结构，块状构造，以中风化为主，节理、裂隙较发育，主要节理为N10°～39°E/E65°～85°S，部分裂隙填充石英脉，岩体较完整，地下水为基岩裂隙水，主要赋存于花岗岩节理、裂隙中，综合围岩等级为Ⅲ级。

图1 厦门芦澳路—疏港通道地下互通立交隧道

区内地貌属沿海低山丘陵地貌。地下水埋藏较浅，为1.0～5.0 m。对工程有影响的地下水主要在冲积层及部分构造储水带中。隧址区地表水较发育，水塘、水库零星分布，地表水流程短、泾流小，自成水系入海。

1.3 隧道设计参数及施工工法

疏港通道分岔隧道采用4种断面(FC2FⅢ、FC3FⅢ、FC4FⅢ、FC5FⅢ)逐步扩大过渡，由大跨段直接过渡至小净距段，如图 2所示。最大过渡断面(FC5FⅢ)为单洞5车道设计，开挖跨度为30.46 m，开挖面积为450.41 m2，采用双层初期支护+二次衬砌的支护设计，大跨段隧道FC5FⅢ型衬砌断面如图 3所示。主线隧道小净距段为单洞3车道设计，开挖跨度为15.65 m，开挖面积为122.53 m2，采用单层初期支护+二次衬砌的支护设计，主线隧道小净距段衬砌断面如图 4所示。匝道隧道小净距段为单洞2车道设计，开挖跨度为12.30 m，采用单层初期支护+二次衬砌的支护设计，匝道隧道衬砌断面如图5所示。疏港通道分岔隧道支护参数如表1所示。

图2 疏港通道分岔隧道平面图(单位： m)

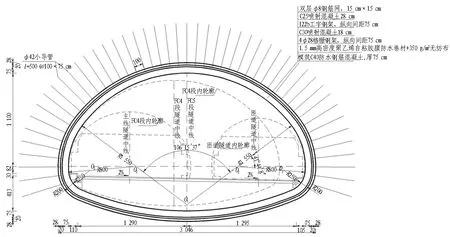
图3 大跨段隧道FC5FⅢ型衬砌断面(单位: cm)

图4 主线隧道小净距段衬砌断面(单位: cm)

图5 匝道隧道小净距段衬砌断面(单位: cm)

表1 疏港通道分岔隧道支护参数

大跨段隧道拟采用主动支护的钢架岩墙组合支撑法施工[14]，开挖进尺为1 m，支护滞后隧道掌子面1 m，钢架岩墙组合支撑法按照①—②—③—④—⑤分部的顺序施工，并施加预应力锚索支护(l=10 m,1 000 kN)；②、③、④、⑤分部分别滞后①分部10、12、22、27 m，如图 6(a)所示。小净距段隧道采用短台阶法施工，主洞隧道先施工，开挖进尺为2 m，支护滞后隧道掌子面2 m，短台阶法按照①—②—③分部的顺序施工，如图 6(b)所示，并对夹岩施加对拉锚杆支护；②、③分部分别滞后①分部6、10 m；同时考虑主洞隧道相应开挖面超前匝道隧道8、16、24、32 m等情况。出于安全考虑，大跨段隧道完成施工后，进行小净距段隧道的施工，同时对大跨段与小净距段隧道交界面采用C25喷射混凝土进行封闭。

(a) 大跨段钢架岩墙组合支撑法

(b) 小净距段短台阶法

2 三轴压缩强度及变形试验

2.1 三轴压缩试验参数

本试验所用标准试件均取自现场掌子面，取样方法为现场钻芯，随后利用切石机进行加工。试样为天然含水状态下的中粗粒花岗岩标准试件，如图7所示，试件直径50 mm，高100 mm。考虑到现场隧道埋深的影响，共设置5种围压工况，围压分别为0、3、5、10、15 MPa。依据GB/T 50266—2013《工程岩体试验方法标准》进行三轴压缩强度及变形试验。

图7 花岗岩标准试样

2.2 三轴试验结果分析

2.2.1 岩石抗剪强度指标计算

不同围压条件下的极限轴向应力，按式(1)计算，得到计算结果如表2所示。

(1)

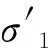
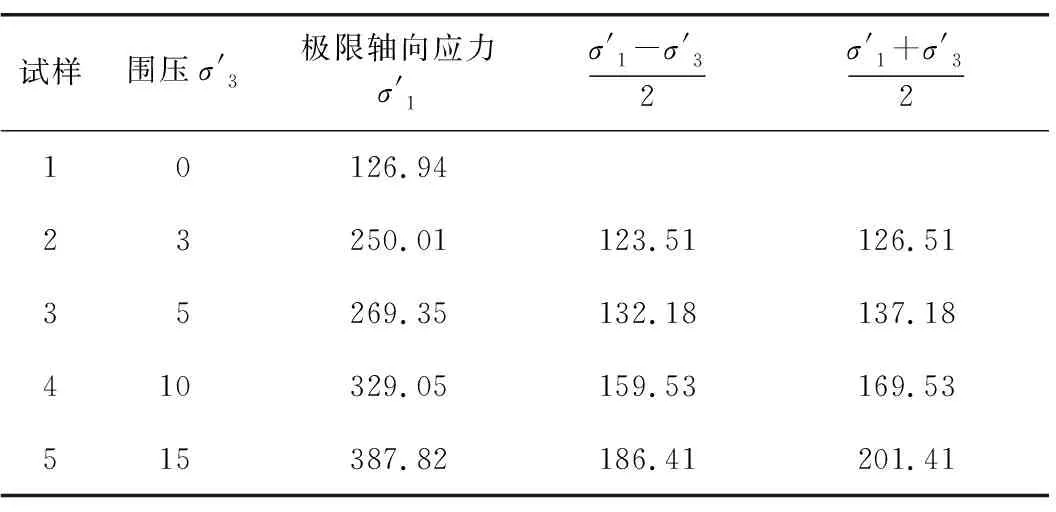
表2 三轴压缩试验数据汇总

由表2可知，在有围压的情况下，随着围压增大，岩石试样极限轴向应力也随之增大。通过试验得到试样单轴压缩强度为126.94 MPa。

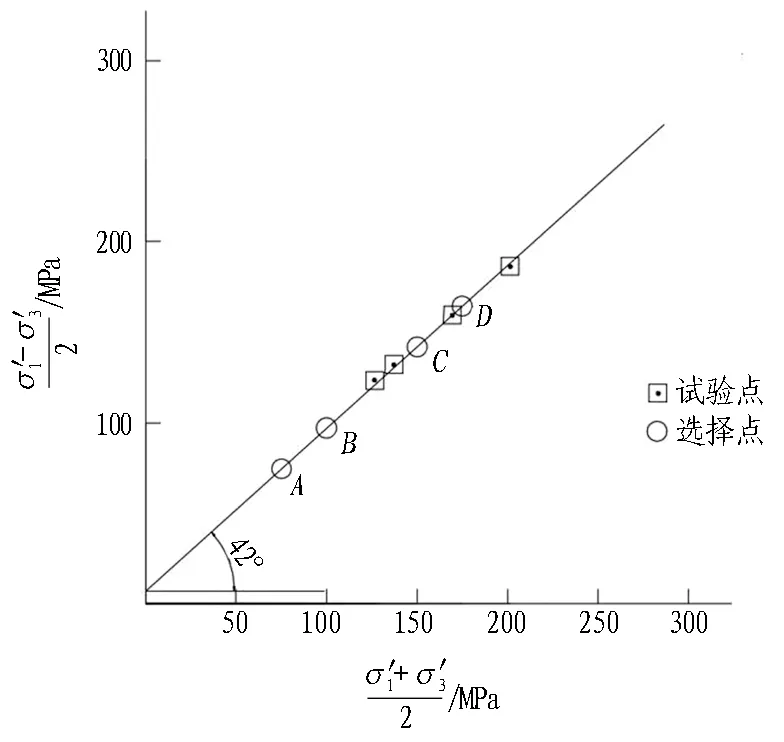
图8 最佳关系曲线

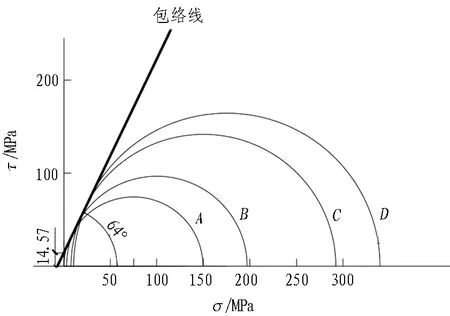
图9 摩尔包络线

表3 最佳关系曲线上选取点数据

2.2.2 岩石应力-应变关系

图10 试样1—5应力差-轴向应变关系曲线

由图10可知，随着围压的增大，岩石试样峰值强度逐渐增大，超过峰值强度后，此时岩石试样内部裂隙继续发展，最后可以观察到峰值强度后的残余应变和残余强度曲线。同时可知，在无围压情况下，试样峰值强度远低于有围压的试样，岩石试样应力-应变曲线几乎为直线，说明本工程花岗岩属于弹脆性岩石，无围压的情况下几乎不存在塑性状态。以上分析说明本工程花岗岩是弹脆性岩石，且岩石处于三向受力状态时的强度和稳定性远大于双向受力状态，应重点关注隧道施工时围岩是否及时处于三向受力状态。

2.2.3 岩石弹性模量和泊松比计算

在纵向应变与应力差的关系曲线上，确定直线段的起始点应力值和纵向应变以及终点应力值和纵向应变。该直线段斜率为弹性模量，按式(2)计算，对应的弹性泊松比按式(3)计算：

(2)

(3)

式(2)—(3)中：Ee为岩石弹性模量，MPa；μe为岩石弹性泊松比；σa为应力与轴向应变关系曲线上直线段起始点的应力值，MPa；σb为应力与轴向应变关系曲线上直线段终点的应力值，MPa；εab为应力为σb时的纵向应变值；εaa为应力为σa时的纵向应变值；εcb为应力为σb时的横向应变值；εca为应力为σa时的横向应变值。

通过以上公式可计算出岩石弹性模量与泊松比，全部试验结果汇总如表 4所示。由表可知，花岗岩试样弹性模量与围压呈正相关。

表4 三轴压缩强度及变形试验结果汇总表

根据三轴试验得到岩块的物理力学参数，结合Hoek-Brown强度准则得到现场岩体的物理力学参数。Hoek-Brown等[15]通过大量岩石三轴试验得到岩体强度普遍估计公式：

(4)

式中：σ1为岩体破坏时最大主应力；σ3为岩体破坏时最小主应力；σc为完整岩块单轴抗压强度；mb、s为岩体Hoek-Brown参数；α为岩体特性决定的常数。

采用基于GSI(地质强度指标)的岩体参数Hoek-Brown估算方法，估算公式如下[15]：

(5)

(6)

(7)

式(5)—(7)中：σtm为岩体抗压强度；σcm为岩体抗拉强度；Em为岩体弹性模量； GSI为岩体的地质强度指标。

结合Mohr-Coulomb强度准则，采用回归分析的方法，可以得出岩体内摩擦角φ和黏聚力c。

(8)

σ1=kσ3+b。

(9)

(10)

(11)

由上述公式可知，岩体Hoek-Brown参数mb和s是确定岩体强度参数的关键，其值可以由式(12)得出：

(12)

式中mi为组成岩体完整岩块的Hoek-Brown参数，花岗岩为33。

当岩体GSI>25[16-18]时，

(13)

当岩体GSI<25时，

(14)

基于文献[19]，并结合现场揭示的岩体结构类型和风化状态，得到施工现场岩体GSI值为55。根据三轴试验的结果，岩块单轴抗压强度σc=126.94 MPa。由式(12)—(14)可得mb=6.61,s=0.006 738,α=0.5。

由式(5)—(7)可得岩体抗压强度σtm=-10.41 MPa，岩体抗拉强度σcm=0.12 MPa，弹性模量Em=15.02 GPa。

由式(4)可得

σ1=σ3+126.94×(0.052 113σ3+0.006 738)0.5。

(15)

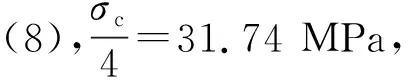
表5 数据回归分析表

(16)

(17)

表5中有6组数据，因此n取6。将表5中的数据代入式(16)和(17)，得出k=5.65，b=31.56；将k、b的值代入式(10)和(11)，得出φ=44.4°，c=6.62 MPa。汇总数值模拟采用的围岩物理力学参数如表6所示。

表6 围岩物理力学参数

3 分岔隧道大跨段过渡小净距段施工力学研究

3.1 数值模拟方案

3.1.1 模型建立

采用FLAC3D进行三维建模计算，大跨段隧道跨度为30.46 m，高为18.71 m，纵向长为70 m；小净距隧道最小净距为1.2 m，主线隧道跨度为15.65 m，高为9.06 m；匝道隧道跨度为12.30 m，高为8.78 m。隧道埋深为100 m，以主洞隧道为准，考虑到隧道开挖边界效应的影响，大跨段隧道与模型的左右和下边界距离取3倍大跨段隧道跨度。三维数值计算模型采用六面体单元进行网格划分。计算模型边界条件为：模型左右侧施加X方向位移约束，底面施加Z方向位移约束，前后侧施加Y方向位移约束，顶面为自由面不施加约束。分岔隧道三维数值计算模型如图11所示。

D为大跨段隧道跨度。

3.1.2 计算参数

数值计算中围岩采用弹塑性实体单元模拟，采用Mohr-Coulomb屈服准则，围岩力学参数由第2.2节中的三轴试验确定。大跨段隧道初期支护采用弹性实体单元模拟；临时支撑采用Shell(壳)单元模拟；预应力锚索和注浆小导管均采用Cable单元模拟。大跨段与小净距段交界面喷射混凝土采用Shell单元模拟。小净距段隧道初期支护采用弹性实体单元模拟，对拉锚杆和砂浆锚杆采用Cable单元模拟。数值模拟中支护结构的计算参数如表 7所示。

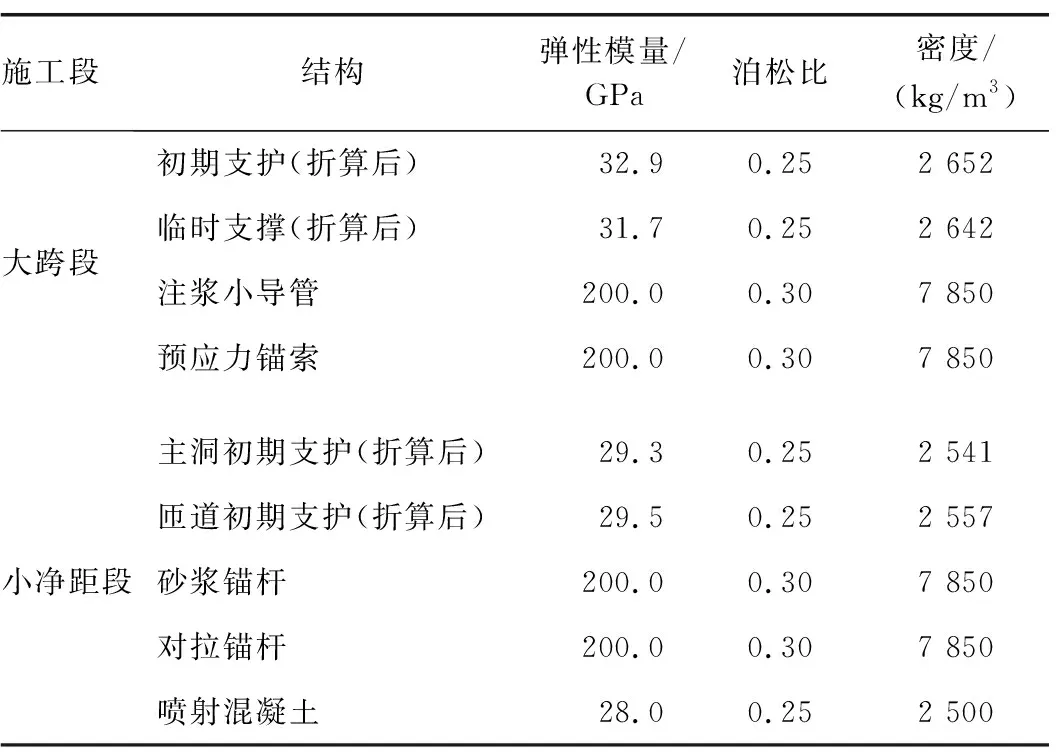
表7 分岔隧道数值模拟计算参数

3.1.3 监测断面

分岔隧道监测断面如图12所示，大跨段选取纵向Y=35 m(断面1)、Y=70 m(断面2)分别为大跨段施工监测断面和大跨段过渡小净距段隧道监测断面。小净距段选取主匝隧道净距分别为1.5 m(Y=72 m，断面3)、3 m(Y=88 m，断面4)、6 m(Y=113 m，断面5)、9 m(Y=131 m，断面6)和12 m(Y=149 m，断面7)处为小净距段隧道施工研究断面。

图12 分岔隧道监测断面设置图

3.2 大跨段过渡小净距段隧道施工力学特性

本节以主洞隧道超前匝道隧道16 m的情况为例，研究小净距段隧道施工对大跨段末端(大跨段与小净距段交界处，Y=70 m)施工力学响应。

3.2.1 大跨隧道交界处围岩变形分析

监测大跨段隧道末端断面各测点的竖直和水平位移增量，得到随施工步变化的位移增量时程曲线，如图 13和图 14所示。

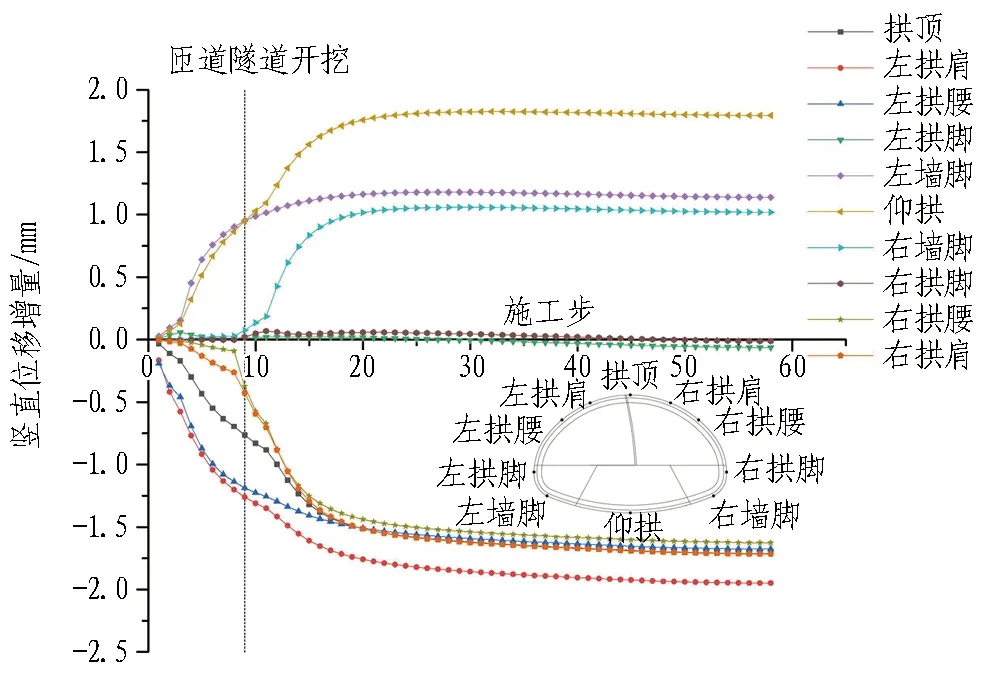
图13 大跨段隧道末端断面竖直位移增量时程曲线

图14 大跨段隧道末端断面水平位移增量时程曲线

由图13可知，左拱肩竖直位移增量最大，最终竖直位移增量为-1.95 mm。拱顶和仰拱则受主洞和匝道隧道开挖的影响，竖直位移不断变化，在第14施工步后拱顶和仰拱竖直位移趋于稳定。由图14可知，左右拱脚水平位移增量较大，最终水平位移增量分别为-0.42、0.40 mm，在第14施工步后左右拱脚水平位移趋于稳定。对比水平位移增量和竖直位移增量可以发现，除左右拱脚外，小净距段隧道开挖对大跨段末端断面的影响主要是竖直方向。为了更为直观地观察大跨段末端测点位移变化规律，统计出小净距段隧道施工引起大跨段末端测点位移变化量，如表8所示。

由表8可知，大跨段左右拱肩部位受小净距段隧道施工影响最大，除了左右拱脚外,其余测点以竖直变形为主，具体表现为拱部测点下沉，而仰拱测点上浮。

3.2.2 大跨隧道交界处初期支护受力分析

监测大跨段隧道末端断面各测点的轴力和弯矩增量，得到随施工步变化的内力增量时程曲线，变化量为正表示弯矩和轴力增大，反之则减小，如图15和图16所示。

表8 大跨段隧道末端测点位移变化量

图15 大跨段隧道末端断面轴力变化时程曲线

由图15可知，除拱顶、左拱肩、右拱肩和仰拱等部位外，其余部位轴力均有不同程度增大，其中左右拱脚轴力明显增大，最终增量分别达1 640.6、1 591.4 kN，这表明小净段隧道的施工会导致大跨段拱脚处应力集中加剧。拱顶和仰拱轴力则明显减小，分别减小212.3、529.0 kN;其他部位轴力变化较小。由图16可知，除左拱脚、右拱脚、仰拱、右墙脚等部位外，其余部位弯矩均有不同程度增大，右拱腰弯矩明显增大，最终增量达19.4 kN·m，右拱脚弯矩则明显减小，最终减小21.4 kN·m；其他部位弯矩变化较小。

总体上来看，匝道隧道开挖前，左拱肩、左拱腰、左拱脚、左墙脚等靠近主洞隧道的部位，轴力和弯矩变化趋于平缓，这说明主洞隧道施工对大跨段隧道靠近主洞隧道的部位内力影响范围为主洞隧道掌子面后16 m(约1倍主洞开挖洞径)。同理也可知，匝道隧道施工对大跨段隧道靠近匝道隧道的部位内力影响范围为匝道隧道掌子面后12 m(约1倍匝道隧道开挖洞径)。

结合第2节的计算结果，可得以下结论：主洞隧道施工对大跨段隧道内力和位移影响范围为掌子面后16 m，匝道则为掌子面后12 m；小净距段隧道施工会引起大跨段隧道末端初期支护不同程度的内力变化，其中左右拱脚处内力变化最为剧烈。

3.2.3 大跨隧道交界处塑性区分析

小净距段隧道施工前后，大跨段隧道与小净距段隧道交界处塑性区如图17所示，为了更直观地观察交界处塑性区变化，图17隐藏了大跨段隧道初期支护。

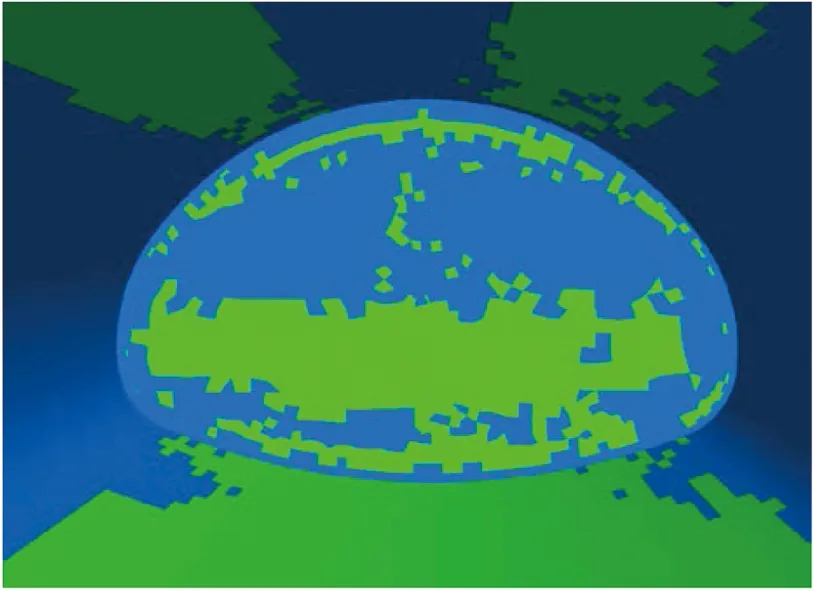
(a) 小净距段施工前

(b) 小净距段施工后

通过对比分析交界处塑性区变化可以发现，小净距段隧道施工完成后，大跨段隧道拱部和仰拱处塑性区有一定发展，表明拱部和仰拱处围岩受拉区域变大。交界面也出现了大面积塑性区，这说明及时对交界面进行混凝土封闭是必要的。同时也可以发现，由于小净距段隧道对上部围岩的支护，小净距段隧道底板处出现了大面积塑性区，因此施工中应当加强小净距段隧道底板的支护强度。

3.3 小净距段隧道施工力学特性

考虑小净距段隧道主洞隧道相应开挖面超前匝道隧道8、16、24、32 m等情况，研究主洞隧道受匝道隧道施工的影响，对比主匝隧道不同纵向开挖间距下主洞隧道受力、围岩变形和塑性区分布的情况，基于此得出小净距段隧道主洞和匝道隧道最佳纵向施工间距。

3.3.1 主洞隧道围岩变形对比分析

以主洞隧道超前匝道隧道16 m的情况为例，全程监测主洞隧道断面4的围岩变形情况，其测点竖直和水平位移时程曲线分别如图18和图19所示。同时对比分析主匝隧道纵向间距为8、24、32 m时主洞拱顶沉降演变规律。

图18 主洞隧道断面4测点竖直位移时程曲线

图19 主洞隧道断面4测点水平位移时程曲线

从整体来看，匝道隧道②部到达断面4后，主洞各部位水平和竖直位移变化均趋于稳定。分析图 18可知，主洞①部到达后拱顶、左右拱肩等拱部上部测点沉降变化速率发生了突变，在匝道隧道②部到达断面4后趋于稳定，拱顶最终沉降为3.05 mm；主洞②部到达后，左右拱腰等拱部下部测点沉降变化速率发生突变，在匝道隧道②部到达断面4后趋于稳定，左右拱腰最终沉降分别为1.67、1.98 mm。左右拱脚竖直位移则很小。分析图 19可知，主洞左右拱脚水平位移变化最为剧烈。右拱脚水平位移表现为先增大后减小，即右拱脚在匝道②部到达前水平位移逐渐增大，朝着匝道隧道方向变形，匝道②部到达支护后，水平位移逐渐减小。左拱脚水平位移则表现为随着匝道隧道施工逐渐增大，在匝道②部到达后趋于稳定。通过以上分析可以发现,匝道隧道初期支护的及时闭合能够有效减小匝道隧道施工对主洞隧道的影响。

表9列出了主匝隧道不同纵向开挖间距情况下，各监测断面拱顶沉降量。在纵向开挖间距一定的情况下，随着隧道净距逐渐增大，主洞拱顶沉降逐渐减小，当隧道净距大于6 m(断面5)时，拱顶沉降接近单洞开挖拱顶沉降量。对比不同纵向开挖间距可知，主匝隧道纵向开挖间距越大，对应断面拱顶沉降没有变化，故可以认为不同主匝隧道纵向开挖间距对拱顶沉降没有影响。

表9 主洞隧道拱顶沉降量

3.3.2 主洞隧道支护受力对比分析

同样以主洞隧道超前匝道隧道16 m的情况为例，全程监测主洞隧道断面4支护受力情况，其轴力和弯矩时程曲线分别如图 20和图 21所示。

匝道②部到达断面4进行支护后，主洞隧道轴力和弯矩变化均趋于稳定。通过分析主洞轴力时程曲线可以发现，左右拱脚轴力远远大于其他部位，左右拱脚轴力分别为-1 392.5 、-1 900.6 kN，拱顶受拉但受拉轴力较小，为36.2 kN；同时可以发现,受匝道隧道近接施工影响，右侧轴力大于左侧对应部位。

结合支护弯矩时程曲线进行分析，左右拱肩在支护后受主洞下台阶②部支护的影响，由负弯矩变为正弯矩，在匝道②部支护后保持稳定，最终分别达到1.02、0.76 kN·m。右拱脚在匝道隧道下台阶②部支护前，弯矩逐渐增大，匝道②部支护后则逐渐减小随后保持稳定。左右拱脚弯矩大于其他部位，左右拱脚弯矩分别为1.62、1.61 kN·m。除拱顶外主洞隧道各部位均可以看作偏心受压混凝土构件并进行强度检算，得到强度安全系数。左拱脚、左拱腰、左拱肩、右拱肩、右拱腰、右拱脚等部位强度安全系数依次为2.73、11.53、57.31、66.24、6.93、2.00。各部位安全系数由高到低依次是右拱肩、左拱肩、左拱腰、右拱腰、左拱脚、右拱脚。拱顶虽然承受拉应力，但所受拉应力远小于C25混凝土抗拉强度，故可认为是安全的。主洞隧道开挖面积超过100 m2为大断面隧道，拱脚处承受巨大的压应力；而匝道隧道近接施工的影响则加剧了主洞隧道拱脚处的应力集中程度，在这2个不利因素的作用下，左右拱脚处的安全系数远小于其他部位。

图20 主洞隧道断面4初期支护轴力时程曲线

图21 主洞隧道断面4初期支护弯矩时程曲线

表10列出了主匝隧道不同纵向开挖间距下主洞隧道初期支护轴力。在主匝隧道纵向开挖间距相同的情况下，随着主洞和匝道隧道净距不断增大，主洞初期支护轴力减小；以主匝隧道纵向间距为8 m时，右拱脚处的轴力变化情况为例，断面3—7右拱脚轴力分别为-3 439.5、-1 729.6、-1 133.4 、-982.9、-872.9 kN。随着净距增大，各断面右拱脚轴力相比断面3依次减小49.7%、67.0%、71.4%、74.6%，这说明主匝隧道净距小于6 m时，主洞隧道各部位轴力变化剧烈；隧道净距大于6 m后，主洞轴力变化趋于稳定，逐渐接近独立单洞开挖时的轴力。

表10 主洞初期支护轴力

以主匝隧道纵向开挖间距8 m时右拱脚轴力为基准，得到各断面右拱脚轴力占比，如图 22所示。由图可知，轴力占比曲线呈先上升后下降的规律。受隧道纵向开挖间距的影响，断面4右拱脚轴力变化幅度最大。主匝隧道净距为1.5 m(断面3)时，右拱脚轴力基本不受隧道纵向开挖间距的影响。随着纵向开挖间距的增大，断面4—7右拱脚轴力则逐渐增大，间距为32 m时断面4右拱脚轴力占比为113.3%，即与间距8 m的情况相比右拱脚轴力增大了13.3%。由此可得：同一监测断面处，主匝隧道纵向开挖间距越大，主洞各部位轴力也越大，左右拱脚应力集中程度也越严重；而随着隧道净距的增大，开挖间距对主洞隧道轴力的影响也相应减小。

图22 主洞隧道右拱脚轴力占比曲线

3.3.3 小净距段隧道塑性区对比分析

对小净距段隧道塑性区对比分析发现：主洞和匝道隧道拱部、底板和夹岩处出现了大面积相连的塑性区。主匝隧道纵向开挖间距为8 m时，小净距隧道夹岩塑性区已经完全贯通；随着主匝隧道纵向开挖间距的增大，小净距隧道夹岩塑性区减小。因此，采用较小的纵向开挖间距虽然能提高小净距段隧道施工效率，但主匝隧道施工相互影响也随之增大，对夹岩受力产生不利的影响。