某地铁横通道掌子面失稳原因分析*
2022-01-22欧阳鹏博王承科肖洪波钟志全任庆国
欧阳鹏博,王承科,肖洪波,钟志全,任庆国
(1.中建五局土木工程有限公司,湖南 长沙 410004; 2.中国建筑第五工程局有限公司,湖南 长沙 410004)
0 引言
新奥法隧道施工过程中,掌子面稳定是安全施工的一种保障。目前,关于掌子面稳定的研究主要包括软弱地层掌子面稳定性分析[1]、核心土对隧道掌子面稳定性的影响[2-3]、采用新奥法施工隧道的围岩变形控制[4]。掌子面稳定性系数也可由超前支护作用于掌子面的地基反力土坡稳定原理求得,超前支护存在最佳布置方式和最佳长度[5-7]。
本文结合湘六区间横通道工况,分析横通道掌子面失稳原因,进而分析小导管破坏原因。
1 Winkler地基模型
Winkler地基模型假设地基由多个独立且满足胡克定理的弹簧单元组成,每个弹簧上的压力p(x,y)与其对应的位移ω(x,y)成正比,比例系数为k,其表达式为:
p(x,y)=kω(x,y)
(1)
式中:k为地基基床系数(kN/m3);p(x,y)为施加在地基上的压力强度(kPa);ω(x,y)为p(x,y)位置上的位移(m)。
小导管超前支护力学模型如图1所示,当l1≤l时,将小导管作为有限长度的Winkler弹性地基梁,其中l为隧道掌子面破裂面在水平方向的投影长度(m),l1为小导管在掌子面后的长度(m),a为掌子面距初期支护的距离(m)。
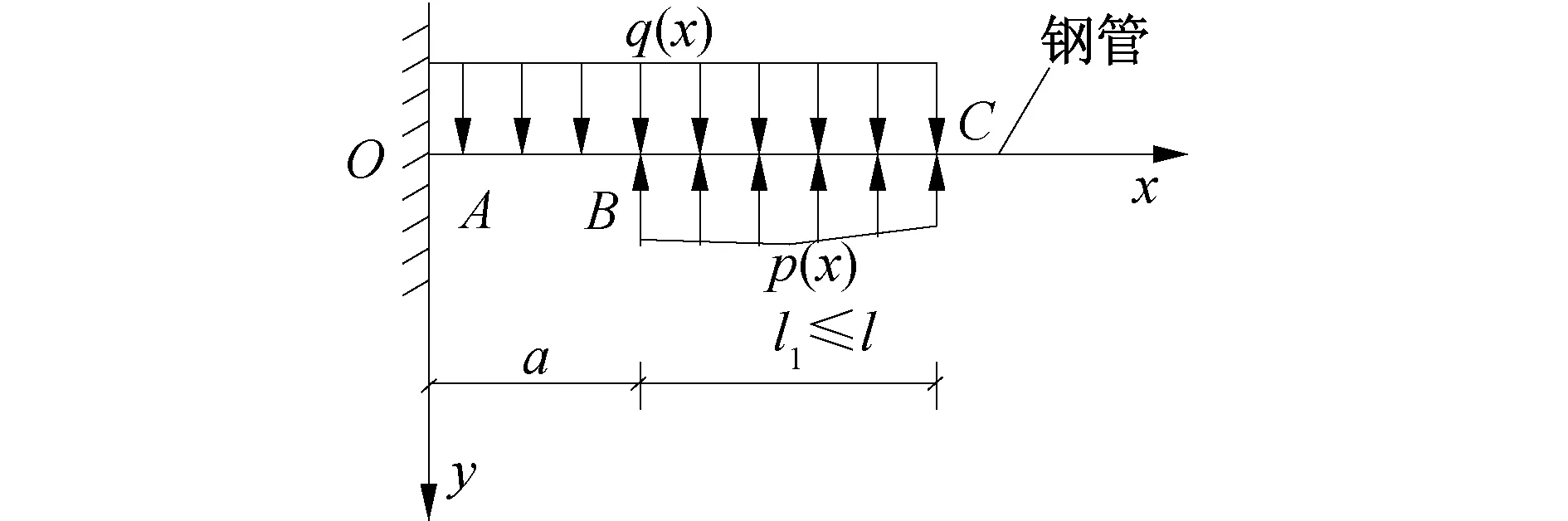
图1 超前支护力学模型
1)微分方程
AB段:
(2)
BC段:
(3)
式中:b为梁宽度(m);q为围岩压力(Pa);E为梁弹性模量(Pa);I为梁惯性矩(m4)。
解微分方程求得挠度方程。
AB段:
(4)
BC段:
(5)
2)转角方程
AB段:
(6)
BC段:
(7)
3)弯矩方程:
AB段:
(8)
BC段:
(9)
4)剪力方程
AB段:
(10)
BC段:
Q2=-EI{2λ3eλx[(-A5+A6)cosλx-
(A5+A6)sinλx]+2λ3e-λx[(A7+
A8)cosλx+(-A7+A8)sinλx]}-
shλ(x-l)cosλ(x-l)]}
(11)
式中:A1~A8为待定系数,由边界条件ω1|x=-a=ω0,θ1|x=-a=0;ω1|x=0=ω2|x=0,θ1|x=0=θ2|x=0,M1|x=0=M2|x=0,Q1|x=0=Q2|x=0;M2|x=l=0,Q2|x=l=0可得如下方程组:
(12)

由式(12)求出待定系数A1~A8,将其带入式(4)~(5),可得小导管任意一点的挠度,将求得的挠度代入式(1),可求得地基反力。
2 掌子面稳定性分析模型
破裂面上方岩体除受其自重外,还受到2种力:①地基反力p(x),地基反力等于小导管作用于地基的力;②围岩压力q(x),围岩压力可由q=γhq= 0.45×2s-1γω求得,其中hq为等效荷载高度值;s为围岩级别;γ为重度;ω为宽度影响系数,ω=1+i(B-5),B为坑道宽度(m);i为B每增加1m时围岩压力的增减率(以B=5m为基准,B<5m时,取i= 0.2;B>5m时,取i=0.1)。小导管作用下掌子面稳定性分析模型如图2所示。

图2 小导管作用下掌子面稳定性分析模型
假设破裂面为潜在滑动面,稳定安全系数K为滑动面上抗滑力R与下滑力S的比值,即:
K=R/S
(13)
隧道掌子面边坡岩体提供的抗滑力为:
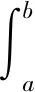
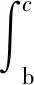
(14)
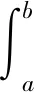
隧道掌子面岩体提供的下滑力为:
(15)
由式(13)~(15)得到稳定安全系数K为:
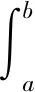
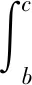
(16)
3 案例分析
3.1 工程概况
湘雅三医院站—六沟垅站区间位于岳麓区,区间始于湘雅三医院站,左线全长891.874m,右线全长892.91m。本区间埋深较大,最小埋深约17m,最大埋深约33m。隧道穿越范围岩层主要为强风化、中风化、微风化板岩,局部存在构造角砾岩,区间大里程段存在F20断裂带。
设竖井横通道,与区间正线垂直相交,洞身范围主要为中风化及微风化板岩,局部存在全风化板岩软弱夹层,横通道采用上下台阶法开挖,上台阶分为上导坑和下导坑。横通道上台阶第12榀开挖时掌子面失稳破坏。
勘察设计文件中横通道右侧拱顶处为中风化板岩,其初期支护按IV级围岩设计,而在实际施工中,揭露围岩为全风化板岩,与勘察设计文件中不符,施工时掌子面失稳破坏,如图3所示。

图3 掌子面失稳和小导管破坏
根据勘察设计文件,计算力学参数如表1所示。

表1 计算力学参数
横通道上台阶上导坑高3m,埋深28m,宽6.9m,开挖进尺1.2m,即隧道未支护段长1.2m。A端(见图1)初始位移ω=4mm。小导管采用直径42mm、壁厚3.5mm、长3.5m的钢管,插入掌子面前方围岩1m。钢管弹性模量E1=210GPa,砂浆弹性模量E2=23GPa。单根钢管等效弹性模量E根据E=(E1I1+E2I2)/(I1+I2)求得。利用Maple数值计算软件进行计算分析。
3.2 稳定性分析
将参数代入Winkler地基模型和掌子面稳定性分析模型中得到掌子面稳定性系数,中风化板岩掌子面稳定性系数为5.734,全风化板岩掌子面稳定性系数为0.896<1,可知掌子面在中风化板岩中非常稳定,而在全风化板岩中失稳破坏。
因掌子面失稳,不能为小导管提供地基反力,即小导管只受拱顶围岩压力,因此,小导管尾端弯矩急剧增加,直至破坏。
无小导管支护时,将参数代入掌子面稳定性分析模型中得到掌子面稳定性系数,中风化板岩掌子面稳定性系数为3.445,全风化板岩掌子面稳定性系数为0.564<1,可知无小导管支护时,中风化板岩和强风化板岩的掌子面稳定性系数减小。
由于围岩情况与勘察设计文件不符,围岩支护不利,因此建议采用地质雷达对掌子面前方围岩进行扫描,若掌子面前方围岩情况与勘察设计文件不符,应及时改变支护方案。
4 掌子面前方小导管长度对其稳定性的影响
掌子面前方小导管长度在破裂面水平投影范围内时,按本文计算模型计算掌子面稳定性系数;在破裂面水平投影范围外时参考文献[8]的计算模型计算掌子面稳定性系数。不同围岩掌子面前方小导管长度与掌子面稳定性系数的关系如图4所示,其中中风化板岩中l为1.628m,全风化板岩中l为2.179m,l1≤l为有限长,l1>l为半无限长。
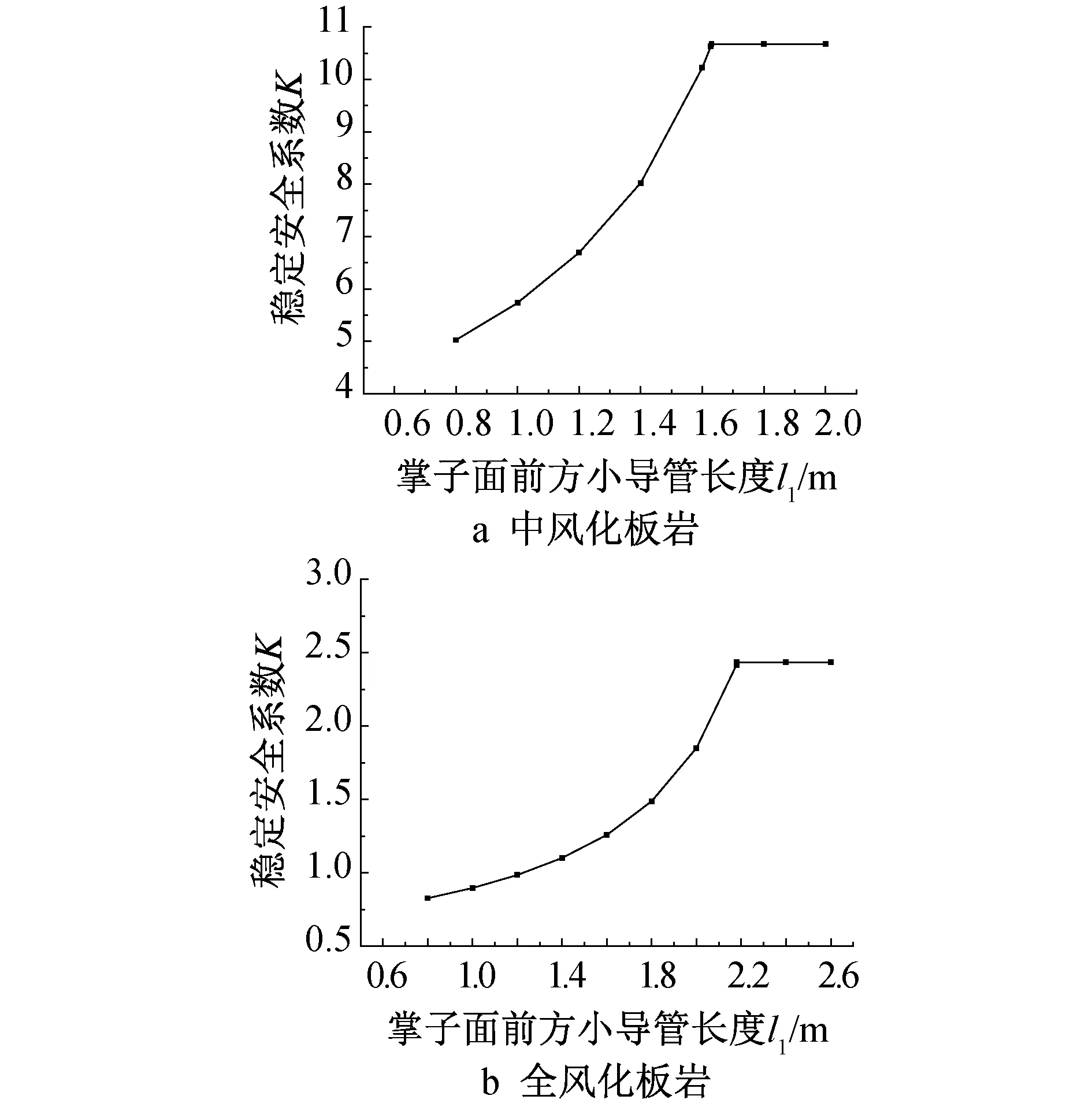
图4 掌子面前方小导管长度对稳定性的影响
由图4可知,全风化板岩和中风化板岩中掌子面稳定性系数随掌子面前方小导管长度的增加先增加后趋于平稳,l1≤l时为增加段,l1>l时为平稳段。
5 结语
1)基于Winkler地基模型得到的地基反力,通过掌子面分析模型及刚体极限平衡理论,得到隧道掌子面安全稳定系数计算方法,当稳定安全系数K<1时,隧道掌子面易失稳破坏。
2)通过计算稳定安全系数,当隧道围岩由中风化板岩变为全风化板岩后,隧道掌子面稳定性系数<1, 掌子面易失稳,且在实际施工中,掌子面产生破坏,证明计算方法正确。
3)掌子面稳定性系数随小导管长度的增加先增大后趋于平稳,l1≤l时,掌子面稳定性系数增加幅度随掌子面前方小导管长度的增加而增加;l1>l时,其值趋向平稳。在全风化板岩条件下,l1>1.3m时,掌子面稳定性系数>1,因此可采取增加小导管长度的方式保持隧道掌子面稳定。
