基于格网坐标转换法的矢量数据脱密方法研究

张寿选

（1.福建省基础地理信息中心，福建 福州 350003）

越来越多的行业部门在互联网上开展业务和展示数据，大量政务数据在互联网上传输，而国土、林业、规划、环境、交通等行业的业务数据中均包含空间信息。空间数据在公开发布或在非涉密网络传输时，必须考虑数据安全问题，一旦泄密，可能对国家安全和人民利益造成严重危害，因此必须先进行脱密处理。地理信息脱密时，除需删除涉及经济、民生、军事的重要地物外，还需降低矢量数据的平面精度和高程精度，并对矢量数据中的敏感属性信息进行处理。

近年来，学者们提出了很多矢量数据的平面精度脱密方法，如江栋华[1]等构造二维切比雪夫多项式建立脱密模型，实现了几何精度可控的脱密；于辉[2]等提出了利用三角函数对矢量、栅格数据进行一体化可逆的脱密模型；聂时贵[3]等将待脱密数据与1∶25万公开数据进行叠加，在两套数据上选择均匀分布的同名点，利用ArcGIS的空间校正工具对矢量数据的几何图形进行脱密。矢量数据几何精度脱密时，为了便于数据共享，需考虑脱密时保留拓扑特征，吕海洋[4]等提出了基于CSRBF的保持拓扑与几何特征的脱密方法；傅宏[5]对公众版地图地理要素的脱密方法进行了研究，总结归类了地理要素空间精度脱密的处理方法。

通过平移、线性变换、仿射变换、坐标转换参数等方法脱密后，较容易被还原成较高精度的数据，因此脱密模型必须引入随机变量、抖动等，从而提高脱密的安全性。本文将格网坐标转换法应用于矢量数据的平面精度脱密，给出了格网点的生成方法、偏移量的计算方法、内插方法等具体思路，并采用该方法进行了数据的脱密实验和分析。

1 平面精度脱密关键技术

矢量数据的几何图形是由坐标或坐标序列进行记录的，对平面精度进行脱密，本质就是将坐标值增加一个偏移量，这与不同椭球间的坐标转换非常类似，因此本文尝试采用格网坐标转换法进行数据脱密。

ArcGIS的Spatial Adjustment工具中提供了Rubbersheet方法，可查看ArcGIS的帮助文档。即使经过非线性、随机变量等模型脱密，只要有足够的连接点（links），Rubbersheet变换就可以将数据还原成精度很高的数据。利用Rubbersheet方法进行空间变换时，无需已知数据的脱密模型，只需一定数量的均匀分布的连接点即可，且连接点数量越多，还原的精度越高。这对矢量数据平面精度脱密模型提出了更高的要求，简单的非线性处理脱密方法是无效的，因此本文引入格网坐标转换法对矢量数据平面精度进行脱密。

谢年[6]采用格网点转换法进行脱密，内插任意点的坐标时采用双线性内插法，格网点的偏移量采用随机数产生。该方法适用于偏移量分布区间较小的情况，由于利用格网坐标转换法内插任意点偏移量时，相邻格网是独立进行内插的，若格网间的偏移量分布区间较大，则相邻格网内插的偏移量差异就很大，可能会破坏要素间的拓扑关系。谢年[6]指出每个格网进行小范围的坐标偏移，能保证局部细致拟合以及全网连续的效果，实验区间为±2 m。因此，利用格网坐标转换法进行脱密，若偏移量的分布区间较大，就必须解决格网内插偏移量不连续的问题。

2 格网坐标转换法

格网坐标转换法的优势是将空间划分成数量众多的独立格网，每个格网采用不同的偏移参数，如果格网数量达到几十万，即使采用Rubbersheet变换进行还原，需要选择数万个连接点才能获取较高的还原精度，而人工选择如此数量的连接点几乎不可能完成。格网坐标转换法脱密的思路如图1所示。

图1 格网点偏移量计算与内插方法

1）创建随机点。采用格网坐标转换法进行不同椭球坐标系间的转换时，必须有两套坐标系下的重合点。采用格网坐标转换法进行脱密时，将随机点作为重合点，可利用ArcGIS的Create Random Points工具创建随机点。该工具需要指定生成随机点的约束范围、随机点个数、随机点间的最小距离。随机点覆盖范围应大于脱密数据的范围，以便于后续计算格网点的偏移量。

2）生成随机点偏移量。为了提高格网点坐标转换法的抗攻击性，随机点的偏移量必须随机变化。为每个随机点添加x和y方向的随机数，随机数的分布区间根据脱密的精度设置，国家法律法规对数据平面精度有明确要求。

3）创建格网点。创建格网点时需要指定起始点坐标、格网间距、格网点行列数，其中行数、列数可根据格网间距和脱密数据范围确定，格网点必须能够完全覆盖脱密数据范围。格网点的组织方式示意如图2所示，经度间隔与纬度间隔一般设置为相同的数值，“节点1”的坐标是格网的起始坐标。创建格网点时，必须记录每个格网点的行号、列号，用于快速定位任意点所在的格网。

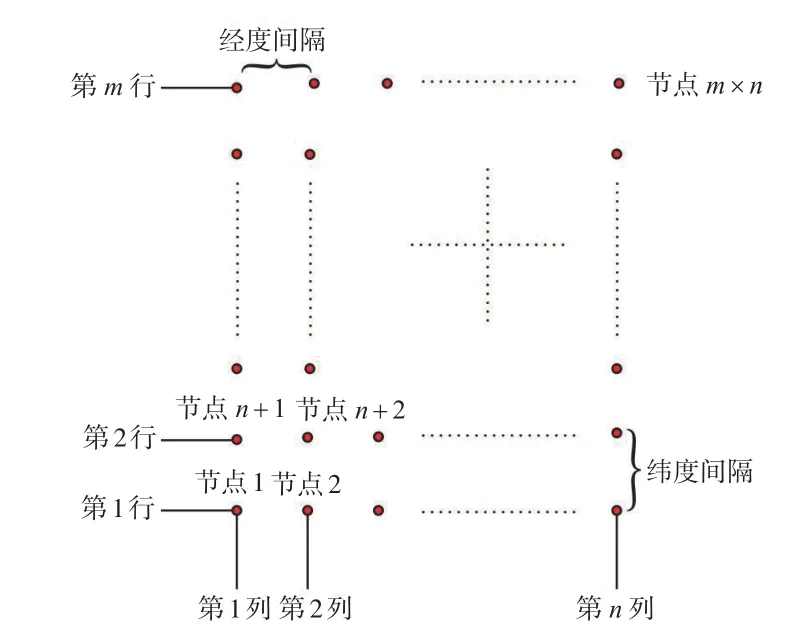
图2 生成格网点示意图

4）计算格网点偏移量。利用移动转换法[7]计算每个格网点的偏移量，搜索格网点gi周围的随机点，选择距离gi最近的k个随机点，采用反距离权重插值法计算格网点的偏移量。为了保证相邻格网点之间的偏移量变化比较平缓，随机点的个数k可适当增加。移动转换法的示意如图1所示。

5）内插任意点的偏移量。对矢量数据平面精度进行脱密，就是内插任意点的偏移量，给任意点的坐标增加一个偏移量。内插任意点p的偏移量时，首先需计算p点所在的格网，由于p点坐标、格网点的起始坐标、格网间距已知，因此很容易计算得到p点所在格网4个格网点的行列号。假设任意点p的坐标为(xp,yp)，格网的起始坐标为(xs,ys)，x和y方向的格网间距分别为dx和dy，则行号r、列号c的计算公式为：

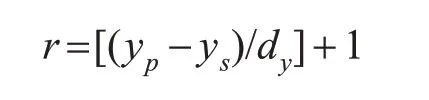
式中，[]为取整。

通过p点所在格网点的行列号，读取4个格网点的偏移量，再基于4个格网点的偏移量利用反距离权重插值法、多项式等方法计算p点的偏移量，本文采用反距离权重插值法。内插任意点偏移量的方法如图1所示。

3 实验与结果分析

3.1 格网生成

以福建省行政区划缓冲50 km的面作为约束范围，本文利用ArcGIS的Create Random Points工具生成106个随机点，随机点之间的最小距离为20 km，最终生成的随机点分布情况如图3所示。生成的随机点并非数量越多越好，而是需要根据随机数分布区间和格网间距确定。偏移量随机数分布区间越大、格网间距越大，随机点之间的最小距离就应设置越大，生成的随机点个数就越少；反之，偏移量随机数分布区间越小、格网间距越小，随机点之间的最小距离就可适当减小，生成的随机点数量就会较多，这样可以保证后期格网间的偏移量变化较小。

图3 随机点分布图

本文利用C#的RNG Crypto Service Provider产生随机种子，利用Random类生成随机数，随机数的区间为[10'50]，生成的偏移量随机数保留两位小数，并写入随机点的属性表中存储。随机点属性表如图4所示。x方向的偏移量为10.16～49.17 m，y方向的偏移量为10.38～48.49 m，与随机点的偏移量区间基本一致，由此可以判断通过控制随机点的偏移量分布区间，可以很好地控制格网点的偏移量，从而影响脱密后矢量数据的平面精度。

图4 随机点属性表

本文采用C#+ArcObjects编写程序创建格网点，格网点的起始坐标为(115'23.4)，格网间距为0.01°，行数为510，列数为630。覆盖范围如图5所示，由于0.01°格网间距的点在小比例尺上显示太密集，无法分辨，因此采用0.07°格网间距进行示意。查询每个格网点周围的随机点，为了保证格网间偏移量变化较小，搜索格网点周围30个随机点，读取随机点的偏移量，再根据反距离权重插值法计算每个格网点的偏移量。格网点x方向的偏移量为10.28～49.17 m，y方向的偏移量为10.39～48.28 m，与随机点的偏移量基本一致。

图5 格网点覆盖范围

格网点的偏移量计算完成后，本文对相邻格网点的偏移量差值进行了分析，编写程序计算每个格网点与周围8个格网点的偏移量差值，x方向的偏移量最大差值为3.86 m，y方向的偏移量最大差值为3.57 m，说明格网之间的偏移量变化较小。格网点采用C#的struct存储行号、列号、顺序号、x坐标、y坐标、x方向偏移量和y方向偏移量，单个格网点的数据结构如图6所示。利用二维数组存储所有格网点，二维数组的下标与格网点的行号、列号对应，方便读取任意点所在格网的4个格网点的偏移量。

图6 格网点数据结构

3.2 脱密实验

本文选取福建省的高速、国道、省道数据进行脱密实验，共计37 656个要素；在工作站上对脱密进行了耗时测试，工作站CPU为Intel Xeon W-2145@3.7 GHz，内存为128 GB 2666 MHz，耗时为79.6 s。脱密结果如图7所示，原始道路与脱密后道路的局部细节如图8所示。

图7 脱密实验道路数据

图8 原始道路与脱密道路细节对比

3.3 结果分析

福建省全省37 656个道路要素，脱密共耗时79.6 s，说明格网坐标转换法具有很高的效率。对脱密后的数据与原始数据进行拓扑检查发现，脱密后的道路中未出现回折、尖角、自相交等拓扑问题，证明格网间的偏移量较平滑，不会破坏拓扑关系。对局部偏移距离进行了量算，某点的偏移量为47.76 m，与该点距离4.6 km的某点的偏移量为49.24 m，两点的偏移量相差1.48 m，脱密后道路的偏移量是变化的，说明偏移量具有较好的随机性。

本文实验的偏移量区间为[10'50]，如果采用从负值到正值的区间，可以增加格网间偏移量的差异，提高脱密后的抗攻击性。实际使用中，偏移量可根据国家规范和文件要求进行设置。为了使格网间偏移量更平滑，可缩小格网间距，能更精细地反映随机点的偏移量。此外，增加格网点的个数会将待脱密数据划分成更多的区域，从而显著提高脱密模型的抗攻击能力。

格网点和偏移量可重复使用。格网点坐标转换法中引入了随机点和随机偏移量，只要保证格网点和偏移量不变，就可以保证同一矢量数据两次脱密后完全重叠。

4 结语

本文将格网坐标转换法应用于矢量数据的平面精度脱密中，通过控制随机点偏移量的分布区间，可以很好地控制脱密后矢量数据的平面精度。随机点和随机偏移量保证了格网间偏移量各不相同，使得矢量数据平面精度脱密后具有很强的随机性，脱密后的数据还原成高精度数据的可能性很低。减小格网间距、增加格网点数量，可以将脱密数据划分成更多的独立区域，从而提高脱密的随机效果。实验采用覆盖福建省的格网点数据，数量达10万以上，利用移动转换法计算每个格网点的偏移量，保证了格网间的偏移量比较平滑，脱密后能保持拓扑关系。