指向“以学定教”的数学教学设计示例——透过“两角差的余弦公式”的视点

淮北师范大学数学科学学院 (235000) 李 雪 张 昆

教是为了不教，学是为了创造.“以学定教”的教学理念强调课堂教学活动不是形成一个个句号，而是调动学生的主观能动性促使课堂教学活动产生一个个问号.教师作为教学活动的引导者，要鼓励学生基于已有的知识经验，寻找新旧知识之间的联系，主动将新知识“挂靠”到原有的认知结构中，从而形成相应的技能、技巧，形成学习能力与养成数学素养.

一、“以学定教”教育理念的基本内涵

“以学定教”顾名思义就是以学生的“学”来确定教师的“教”.“以学定教”中的“学”包含学情和学生两层含义：从学情的角度分析，“学”是指学生原有的知识结构和认知发展水平，同时也包括学生数学思维的深度、数学思想方法的掌握程度以及应用数学知识解决实际问题的能力等；从学生的角度分析，“学”是指教师的教学要面向全体学生，体现人人都能获得良好的数学教育，不同的人在数学上得到不同的发展的基本理念.“以学定教”中的“教”是指教师的教学设计，即教师依据学情分析，基于自身对数学知识的认识设计教学方案，以帮助学生理解和掌握新知识.

教育之设施，以受教者之资质为根据，教育之研究，以受教者之资质为对象[1].由此可见，“学”是为了更好的“教”.这里认为，“以学定教”的真正涵义是教师要坚持“以生为本”的教学发展观，基于学生的实际情况来确定教学顺序、教学方法和教学手段，帮助学生建立起新、旧知识之间的联系，实现学生对新知识的承载与编码.“以学定教”的教学理念要求教师依据学情来设计数学教学方案，并根据学生的课堂回答、行为表现等及时调整教学，以帮助学生自然地、高效地理解并掌握新知识.

二、实现“以学定教”数学教学模式的“三二一”要点

学生的“学”影响着教师的“教”，教师的“教”又反作用于学生的“学”.学生接受新知的过程是一个积极主动的探究过程，是一个发挥人的主观能动性去利用认知结构编写信息从而发挥“运动效应”的过程[2].“以学定教”并非否定教师的“教”，而是要求以“学”为依据来完善教师的“教”.这里基于“以学定教”理念的内涵，提出了该理念指导下的数学课堂教学模式的“三二一”(三原则两关键一核心)要点，以下详细说明之.

(一)三个原则

“以学定教”模式下的数学课堂教学需遵守以下三个原则:

1.教师要注意教导的限度与施教方式

《师说》有云：“古之学者必有师，师者，所以传道授业解惑也.”教师是教学活动的引导者，但绝不能在课堂中“一手遮天”.古希腊著名的哲学家苏格拉底提出的“产婆术”包括讽刺、助产、归纳和定义四个步骤.其中“助产”就是启发、引导学生,帮助学生自主思考，得出结论.由此可见，在数学课堂教学中，教师要注意教导的限度，在教学中适当的“留白”不仅能够激发学生自主思考，还能够增强学生的参与感，激发学生的求知欲.“以学定教”理念指导下的数学教学模式并不是教师一味地给予，学生一味地接受，而是教师依据数学情境，结合学生的最近发展区，启发学生自主探究问题答案.孔子有云“不愤不启，不悱不发.”启发式数学教学具有较好的教育作用，是实现有效数学教学的优化途径与方法，它能调动学生学习的主动性和积极性、促使他们生动活泼地进行数学学习与发现[3].启发式的数学不仅有助于学生编码、应用新知识，还能够提高学生自主学习与解决问题的能力，充分体现“教是为了不教，学是为了创造”的教学理念.

2.坚持学生主体、教师主导的教学理念

波利亚提出的“主动学习”表明，学习任何知识的最佳途径都是自己去发现[4].在数学课堂中，学生是学习的主体，教师要引导学生体验知识的发生发展过程，鼓励学生自主探究、获得新知.传统的“填鸭式”和“满堂灌式”的教学，只体现了教师在课堂中的主导作用，却忽视了学生在数学教学中的主体地位，学生在学习过程中参与感极低，久而久之，便会丧失学习的兴趣.由此可见，教师应坚持学生主体、教师主导的教学理念，进行指向激发学生的学习兴趣，增强学生的数学体验感、调动学生学习的积极性和鼓励学生自主学习探究的数学教学设计.

3.实现以学生发展为本的教学价值追求

“以学生发展为本”是当前课程改革的核心理念，它决定着课堂教学变革的基本价值取向.林崇德教授曾言：“教学的重要任务，是在传授知识的同时，灵活的发展和培养学生的智力与能力[5].”曹才翰教授曾指出：“中学数学所提到的数学能力可以分为两大类，学习数学的能力和创造数学的能力，对这两个处于平行关系的层面再进行细分，又涉及到运算能力、空间想象力、逻辑思维能力和初步应用数学的能力.[6]”教师要在数学教学中有意识地培养学生这四项基本能力，引导学生参与知识的发生发展过程，帮助学生在编码新知识的过程中提升数学能力，掌握数学方法，真正做到以学生的发展为本.

(二)两个关键

三个原则是宏观视角下“以学定教”理念对数学教学的要求.从微观视角来看，“以学定教”理念对数学教师的教学设计也提出了标准，即要求教师在教学时既要提出“好”的问题，又要自然地展现知识的发生发展过程.

1.提“好”的问题

问题是学生思维迸发的泉眼.在实际教学过程中，教师只有提出“好”的问题，才能激发学生的求知欲，主动发生思维活动.“好”的问题不仅能够提高学生学习数学的兴趣，还能够在学生参与教学活动的过程中，增强学生的满足感并建立学习自信.符合以下标准的问题才能称作“好”的问题：其一，与课堂有关，有深刻意义；其二，扎根于合适根据地，围绕“最近发展区”；其三，指向数学本质与核心.

2.自然地展现数学知识的发生发展过程

教师要依据课本所提供的知识素材，设计符合学生知识基础和认知水平的教学设计，选择“合适根据地”，确定最近发展区，引导学生自然地体会知识的发生发展过程，实现对新知识的承载与编码.教师在教学中要借助数学情境，鼓励学生寻找新旧知识之间的联系，以此来体会学习新知识的意义与必要性，帮助学生顺利地、自然地将新知识纳入原有的认知结构.

(三)一个核心——围绕学情设计教学

学情分析是教学设计的基础.教师只有充分了解学生的基本情况，才能“量体裁衣”，因材施教.这要求教师需要把握学生发生数学知识认识时的心理活动，明确发生数学知识认识的心理序列，掌握学生的认知起点，基于教学内容选取合适的教学方法.教师要建立“合适根据地”，设计基于学生“最近发展区”的教学.倘若教学内容的难度过高，学生便难以理解、吸收；若教学内容过于简单，则不利于学生能力的提升.由此可见，教师唯有充分了解学生，进行真正符合学生知识基础与认知水平的教学，学生才能有所收获.

三、“以学定教”理念指导下的“两角差的余弦公式”教学设计

俚语有言：“理在用时方知妙”.真正进行指向“以学定教”的教学不是一件容易的事，需要教师基于课堂教学模式的“三二一”要点设计教学，这没有一个固定的教学模式可以规范性地执行，为此，这里以“两角差的余弦公式”教学设计为例加以说明.

(一)创设情境、引入课题

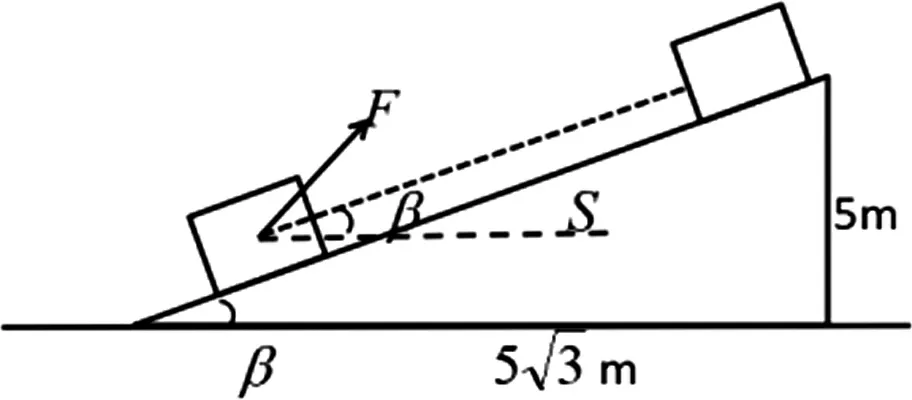
图1

生：W=|F|·|S|cos(45°-β)=30cos(45°-β).

师：很好.只要我们能够求出cos(45°-β)的值，我们就可以得到答案.我们如何才能求出它的值呢？

师：cos(45°-30°)=cos15°的值为多少？

生：不是特殊角度，我们只能通过计算器求解.

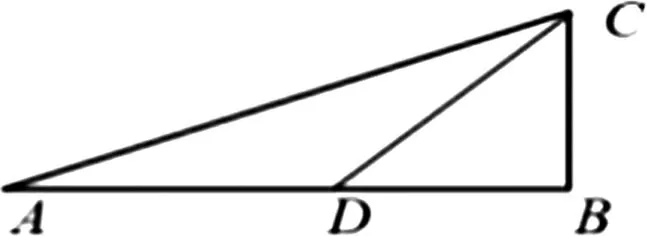
图2

师：我们不能每次都构造直角三角形来求解非特殊角度的余弦值，大家观察cos(45°-30°)这个式子，我们能不能借助已经学过的特殊角度的三角函数值求出cos15°呢，大家大胆猜测一下？

生：我猜cos(45°-30°)=cos45°-cos30°.

师：这个猜测正确吗？

师：大家想一想，还可以写成什么形式呢？

设计意图：这里由物理情境引出亟待解决的问题，即求解cos(45°-30°)=cos15°.基于学生已经掌握的数学知识，并不能快速、准确地求出答案，但cos15°是由学生熟悉的特殊角度组合而成的，故而教师引导学生借助四个特殊角度的三角函数来解决问题.这其实就是两个关键中的“好”的问题.这里的问题能够帮助学生体会到解决问题的迫切性，也符合了“好”的问题的三个要求：既与所要学习的新知识——两角差的余弦公式相关，又立足于学生的最近发展区，从学生已有的知识结构中调取知识，鼓励学生自主解决问题，也体现了数学知识的本质与核心.

(二)设置悬念、激发矛盾

师：应该如何运用特殊三角函数值求解出cos(45°-30°)呢？大家思考一下，我们之前有没有学过形如cos(45°-30°)的公式呢？

生：我们以前学过的诱导公式也是求解两角差的余弦公式.

师：很好，形式确实很相似.同学们观察下面四个诱导公式，有什么发现？

生：四个诱导公式变成了cos(α-β)的形式，其形式与cos(45°-30°)更相似了.

师：也就是说，如果我们能得到cos(α-β)的展开式，我们就能够找到求解cos(45°-30°)的简便方法.大家参考四个诱导公式，可以发现cos(α-β)的展开式都含有哪些元素吗？

生：sinβ、cosβ一定有.

师：很好.假设我们调换二者的位置，那么cos(α-β)又可以转化为何种等价形式？表达式里还有其他元素吗？

生：cos(α-β)=cos[-(β-α)]=cos(β-α)，所以还可能会有sinα、cosα.

三角函数式cos45°cos30°sin45°sin30°三角函数值22322212

师：我们得到了两种答案，哪一种更合理呢？

生：①式更合理，我们可以通过cos(90°-60°)=cos30°代入验证.

师：很好.由此我们得到cos(α-β)=cosαcosβ+sinαsinβ③.

设计意图：在此环节，既体现了一个核心——围绕学情展开教学，又体现了教学时应该遵守的三个原则.教师基于学生已经掌握的诱导公式引导学生探究两角差的余弦公式，帮助学生借助头脑中已有的旧知识编码新知识，不仅有助于学生对新知识的理解和掌握，还能够提高学生的数学自信与参与感.在探究两角差的余弦公式基本形式的过程中，充分体现了学生主体、教师主导的教育理念和以学生发展为本的教学价值追求.学生是学习的主人，这里的教学设计充分发挥了学生的主体地位.学生不是被动的接受知识，而是根据已有的知识经验主动探究两角差的余弦公式的基本形式.在这一过程中，学生的运算能力与逻辑思维能力也得到了提高，真正做到以学生发展为本.除此之外，教师也注意了教学中教导的限度与施教方式.教师所提出的问题为学生留出了足够的思考空间，旨在借助适当的“留白”和启发式的教学方式鼓励学生独立思考，提高解决问题的能力.

(三)提出猜想、积极验证

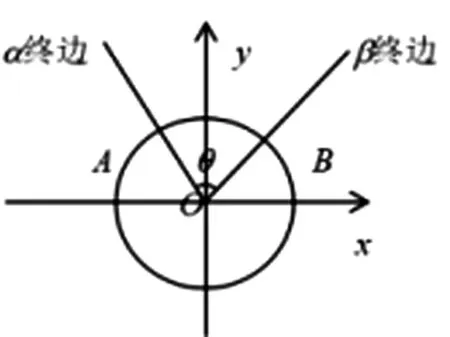
图3

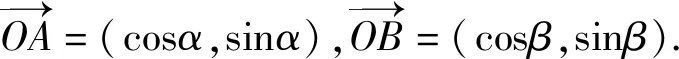
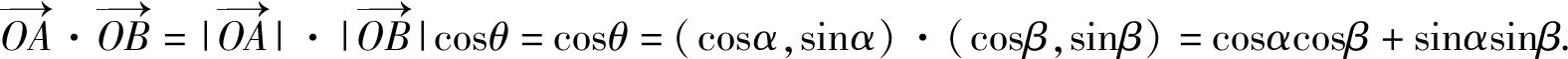
师：由于cosθ=cos(α-β)，我们就验证了cos(α-β)=cosαcosβ+sinαsinβ.

师：同学们继续思考，若α、β在其他象限，即α-β∉[0，π]的情况下，结论还会成立吗？

生：当α-β∉[0,π]时，则存在k、m∈Z，使得α-β=2kπ+θ或β-α=2mπ+θ，即cos(α-β)=cosθ，cos(α-β)=cosθ=cosαcosβ+sinαsinβ.

师：非常正确.这就是我们这节课所要学习的两角差的余弦公式，即cos(α-β)=cosαcosβ+sinαsinβ.

设计意图：这里以平面向量为工具，引导学生证明自己的猜想——两角差的余弦公式的基本形式.基于学生已经掌握的平面向量的有关知识，引导学生求解两向量之积，从而证明了猜想的合理性.这种教学方式自然地展现了知识的发生发展过程，教师环环紧扣，帮助学生顺利地运用已有的知识推导出两角差的余弦公式，学生便自然地将新知识“挂靠”到原有的认知结构中.

(三)学以致用、例题讲解(略)

(四)小结评价、作业布置(略)

四、简要结语

“以学定教”教学思想指导下提出的“三二一”数学教学模式要点能帮助教师设计出真正适合学生学习的教学.首先，教师在教学前必须充分了解学生的知识水平与认知方式，基于学情设计教学；其次，在教学设计中要抛出“好”的问题激发学生的求知欲，用适当的课堂“留白”和启发式的教学模式引导学生自然地体会知识的发生发展过程，贯彻和落实学生主体、教师主导的教学理念，坚持以学生的发展为本，提高学生的运算能力、空间想象力、逻辑思维能力和初步应用数学的能力；最后，帮助学生真正掌握和理解新知识，并实现新知识的承载与编码，将新知识融入到原有的认知结构中.这便实现了基于“三二一”要点的数学教学设计，也真正体现了“以学定教”教学思想的真正内涵与意义.