公铁两用吊拉组合体系桥结合部参数

朱旺华, 李文武, 王会利,1b*

(1. 大连理工大学 a. 桥梁与隧道安全技术国家与地方联合实验室,b. 工业装备结构分析国家重点实验室, 辽宁 大连 116023;2. 湖南省交通规划勘察设计院有限公司, 湖南 长沙 410200)

吊拉组合体系桥兼顾了斜拉桥和悬索桥的优点, 在改善桥梁跨越能力的同时也能提高结构的整体受力性能[1-4].目前建成的吊拉组合体系桥较少,多处于方案阶段,主要原因是斜拉桥和悬索桥属于2种受力完全不同的结构形式.多位桥梁专家和学者对斜拉段与悬索段结合部位刚度变化大、结合区域吊杆疲劳问题进行了研究[5-6];谢宏伟等[7]和唐亮等[8]在相同载荷分配比例条件下,分析了重叠吊杆数量、过渡段主梁刚度等参数对结合部的影响;曾前程[9]对不同的结合部载荷分配比例下的模型进行了运营阶段移动活载分析,总结出过渡区斜拉索分得恒载比例越大,其在运营阶段下的内力越合理,整体刚度也相对更合理;Wang等[10]通过非线性分析得到了主梁、主塔在活载作用下不同矢跨比和主梁拱度下的弯矩和位移.

本文以某主跨为1 152 m的公铁两用吊拉组合体系桥设计方案为例,通过分步计算法获得合理成桥状态,在此基础上分析重叠吊杆数和载荷分配比例2个主要参数对结合部的应力和位移的影响规律.

1 桥梁概况

某主跨为1 152 m吊拉组合系桥设计方案,本桥结构体系为塔梁分离、塔墩固结形式,边跨主缆与斜拉索为全部地锚式,中跨钢梁与边跨地锚梁固结,桥跨布置见图1.孔跨布置为(397+1 152+397) m,主缆中跨矢跨比为1∶6,跨中纯悬索区段长452 m,结合部交叉索8对,交叉区段长98 m,斜拉段长252 m.

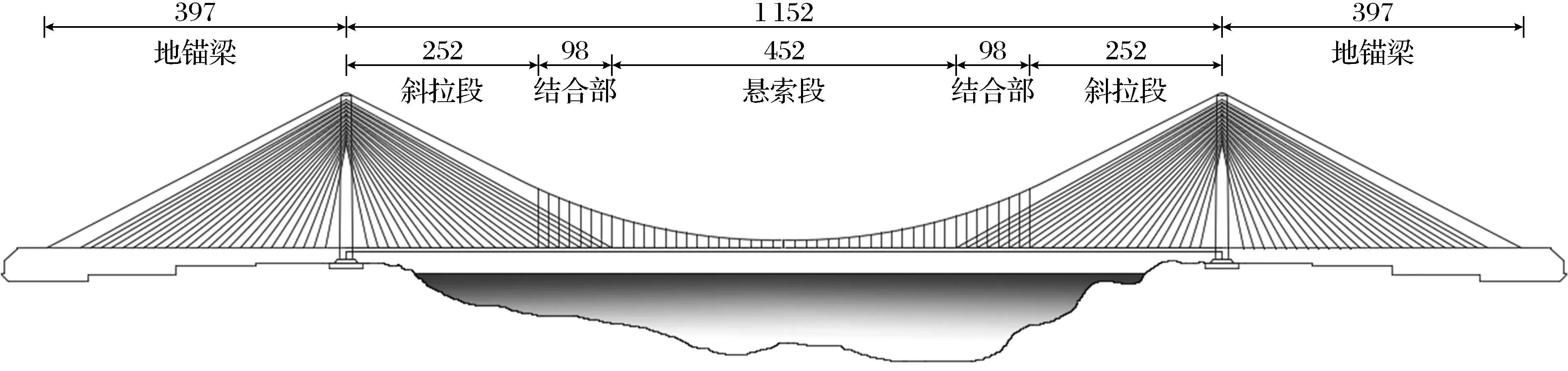
图1 桥跨布置(单位:m)Fig.1 Bridge span arrangement (unit: m)

桥塔为倒Y形塔,塔高210 m,锚索区高度57.5 m(23×2.5 m),主梁采用由3个流线型扁平箱组成的分离钢箱结构,梁宽67 m,梁高5 m.梁上斜拉索、吊杆纵桥向间距14 m,悬索段中间5根吊杆间距15 m,箱梁内横隔板间距2.8 m,中间铁路箱宽13 m,两侧公路箱宽17 m,风嘴宽2 m.为提高3箱受力的一致性,公路箱和铁路箱间采用箱形横梁连接,箱宽2.8 m,间距14 m.桥塔立面及主梁横截面见图2,截面参数见表1;斜拉索共192根(24×4×2),规格为PES7-241～547,主缆规格为151-127Φ5.5 mm,重叠区端吊杆及非重叠区吊杆规格为PES7-139,重叠区中间吊杆为PES7-91.

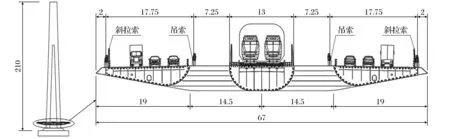
图2 桥塔立面及主梁横截面(单位:m)Fig.2 Bridge tower elevation and main beam cross section (unit: m)

表1 截面主要参数Table 1 Main parameters of section

续表1

2 合理成桥状态确定

吊拉组合桥全桥计算模型(由于全桥的对称性,仅给出一半模型)如图3所示,主梁、桥塔采用梁单元模拟,主缆、吊杆和斜拉索采用索单元模拟,分离式钢箱梁采用单梁模拟.

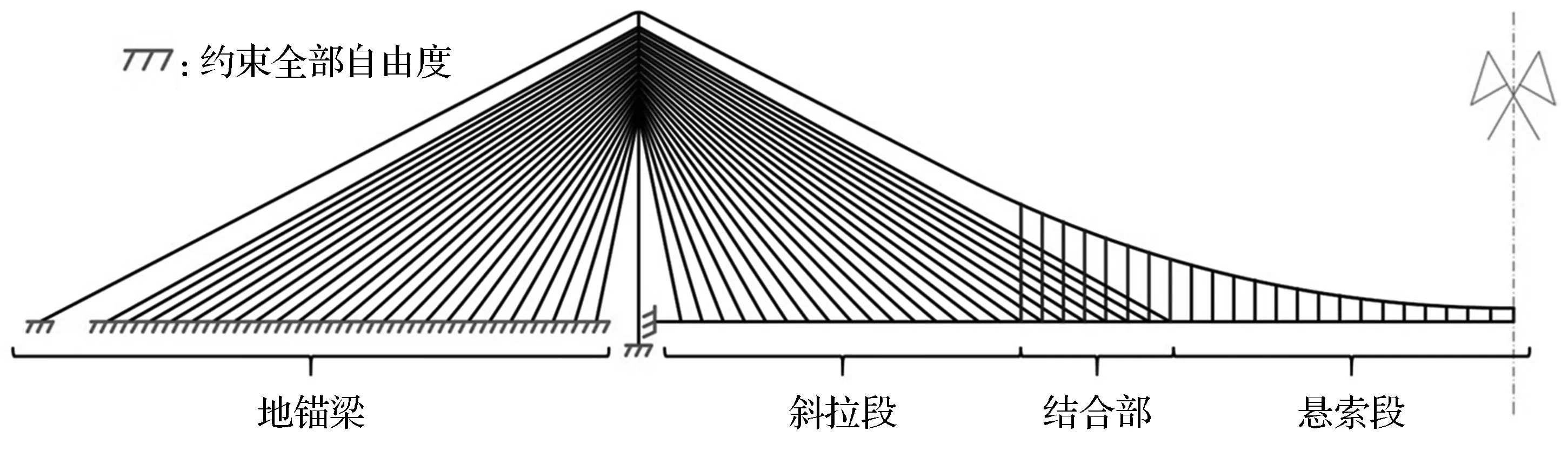
图3 全桥计算模型Fig.3 Full bridge calculation model

合理成桥状态采用分步计算法[11],将吊拉组合体系桥拆分为斜拉桥部分和悬索桥部分,分别进行合理成桥状态计算,最后整合2部分模型,进行几何非线性分析,获得合理成桥状态.

2.1 斜拉桥部分合理成桥状态确定方法

斜拉桥部分为边跨全部地锚式,采用影响矩阵法进行合理成桥状态计算,假定在调整阶段结构满足线性叠加原理,根据影响矩阵的定义可知[12-13]

AX=D.

(1)

式中:A为影响矩阵;X为施调向量;D为受调向量.

在斜拉桥合理成桥状态确定过程中,将结合部重叠吊杆分配的恒载以节点载荷的形式施加在相应节点上,斜拉桥部分计算模型如图4所示,斜拉索输入单位初始索力后,进行计算获得影响矩阵,求解线性方程组(1)获得几何线性状态下的初步成桥状态索力,最后进行几何非线性分析微调索力获得最终成桥状态.

2.2 悬索桥部分合理成桥状态确定方法

悬索桥部分利用节线法初步确定主缆线形,节线法是利用桥梁自重和主缆张力的平衡方程计算主缆坐标和主缆张力[11,14].将结合部分配的恒载及纯悬索段恒载以节点载荷的形式作用在主缆的吊点上,利用主缆竖向平面内力的平衡[11],可初步确定初始的几何形状和主缆的水平张力.

建立悬索部分有限元模型,以主缆吊杆下端节点竖向位移为目标,更新迭代主缆及吊杆无应力索长及节点坐标,直到误差达到容许范围[15],悬索部分计算模型如图5所示.

图5 悬索部分计算模型Fig.5 Calculation model of suspension bridge

2.3 整体模型计算结果

整体模型最终合理成桥状态计算结果如图6、图7所示,主梁弯矩均匀,呈多弹性支承连续梁状态,位移值在-3～5 mm区间;桥塔弯矩较小,基本成轴压状态,主塔水平最大位移为0.13 mm,接近于0.

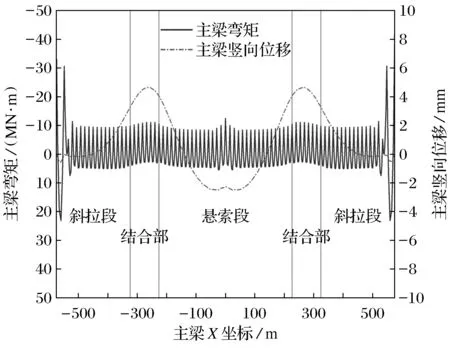
图6 主梁弯矩和位移Fig.6 Bending moment and displacement of main beam

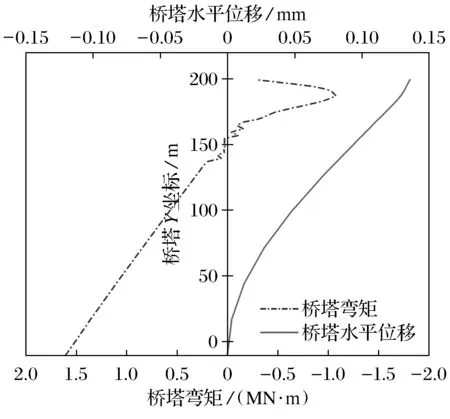
图7 桥塔弯矩和位移

3 结合部参数分析

根据设计方案,该桥为公铁两用桥,双线客运专线,ZK活载;高速公路,6车道,公路-Ⅰ级.根据《公路与铁路两用桥梁通用技术要求》(JT/T 1246—2019)[16],并参考既有公铁两用斜拉桥设计中采用的活载组合折减系数,公路活载折减系数为0.75,铁路活载不折减.载荷工况为1.2恒载+1.4活载.根据影响线确定活载加载方式,将活载等效为静力载荷加载在有限元模型上,然后进行几何非线性分析.

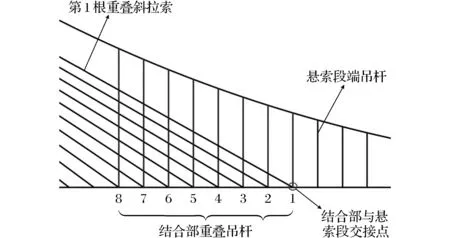
图8 结合部布置Fig.8 Arrangement of connection part

针对吊拉组合体系桥结合部的合理设计问题,综合考虑重叠吊杆数N和载荷分配比例λ(载荷分配比例定义见式(2))2个主要参数对结合部的影响,进行参数分析.关注结合部在活载作用下吊杆和斜拉索应力幅过大造成的疲劳问题,以及结合部主梁平顺过渡问题.结合部吊杆和斜拉索重叠情况以及结合部与悬索段交接点(位移提取点)如图8所示.

λ=G1∶G2.

(2)

式中:G1为结合部吊杆承担的恒载;G2为结合部斜拉索承担的恒载.

3.1 吊杆和斜拉索应力幅

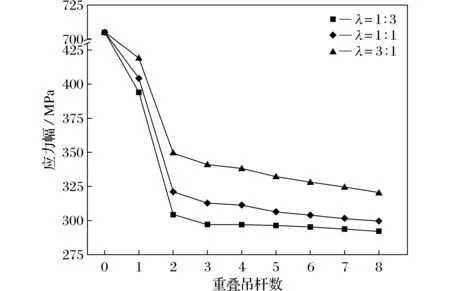
图9 悬索段端吊杆应力幅Fig.9 Stress amplitude of the boom at the end of the suspension section

图9给出了不同载荷分配比例下,悬索段端吊杆应力幅随重叠吊杆数N的变化曲线,随着重叠吊杆数的增加,端吊杆应力幅迅速下降,重叠吊杆数达到3根后,悬索段端吊杆应力幅变化趋于平缓,同时可以看出载荷分配比例λ越大,端吊杆应力幅也越高.

图10、图11分别给出第1根重叠吊杆应力幅和第1根重叠斜拉索应力幅随重叠吊杆数N的变化曲线,由图10可以看出,第1根重叠吊杆应力幅变化规律与端吊杆类似,随着重叠吊杆数N的增加压力幅迅速下降,重叠吊杆数达到4根时趋于平缓.由图11可以看出,增设重叠吊杆也可以降低第1根斜拉索应力幅,但随着重叠吊杆数N的增加,斜拉索应力幅变化并不明显,受载荷分配比例λ影响较大.

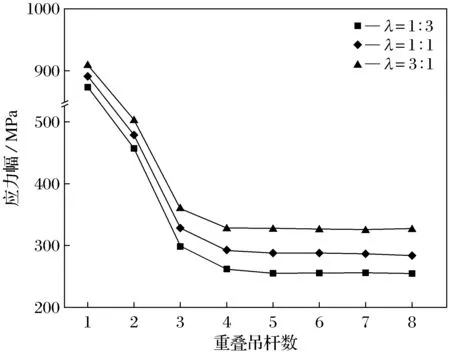
图10 第1根重叠吊杆应力幅

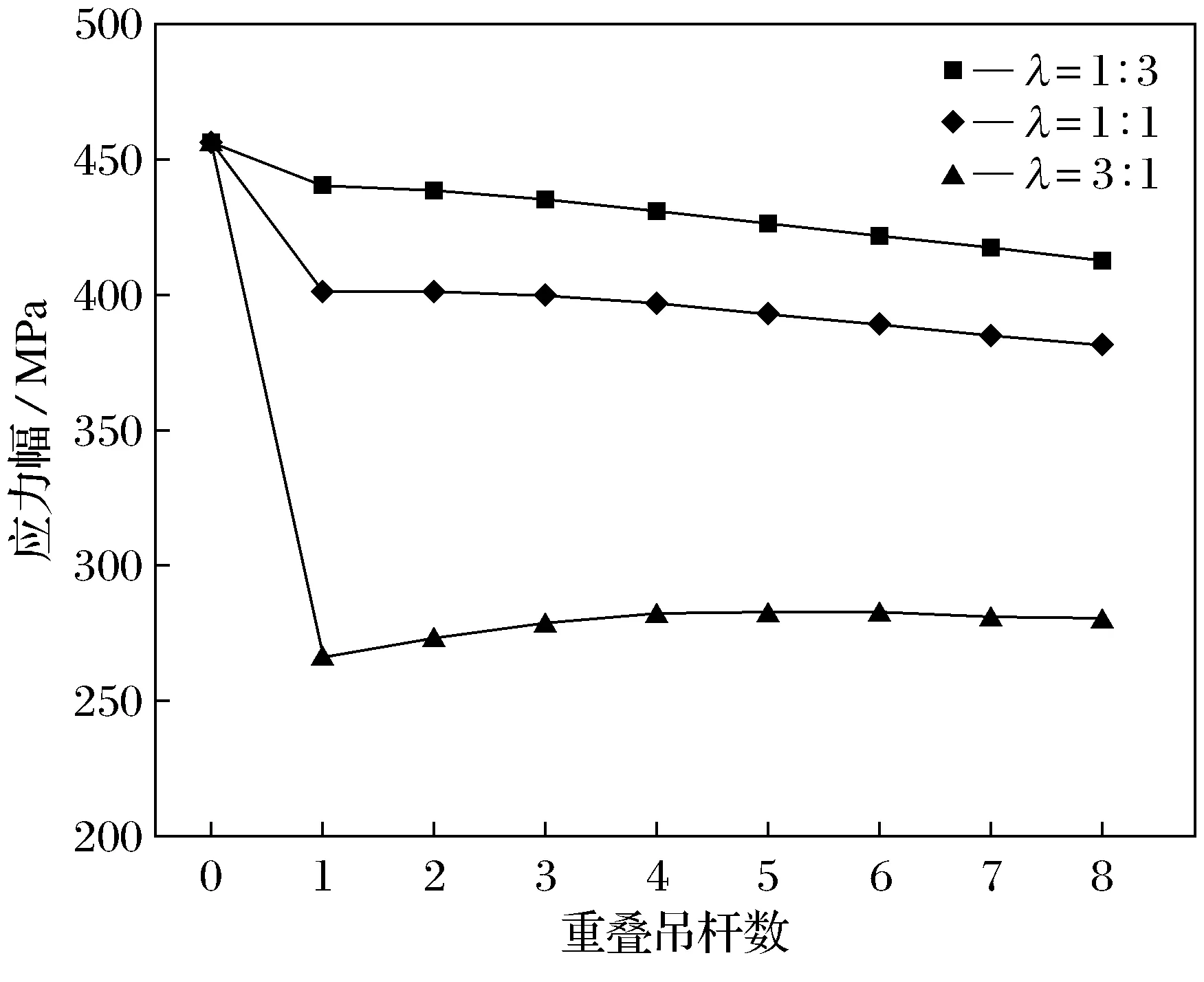
图11 第1根重叠斜拉索应力幅

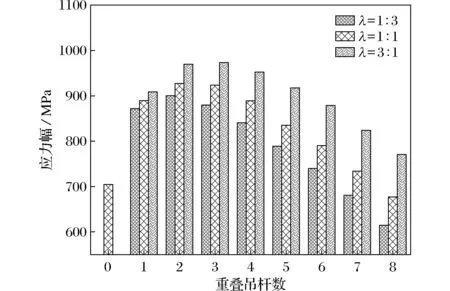
图12 重叠区端吊杆应力幅Fig.12 Stress amplitude of the boom at the end of connection part

通过对计算结果的分析发现,由于主缆在斜拉段为无吊杆段,结合部重叠端吊杆(最外侧重叠吊杆)应力幅高于其他重叠吊杆.图12给出了不同重叠吊杆数下结合部重叠端吊杆应力幅值,从图12可以看出,结合部端吊杆应力幅随着重叠吊杆数的增加呈现先上升后下降的趋势.

3.2 结合部与悬索段交接点位移幅值

图13和图14给出了不同载荷分配比例下, 结合部与悬索段交接点位移幅值随重叠吊杆数的变化曲线. 由图可见,随着重叠吊杆数增加, 结合部与悬索段交接点竖向转角幅值逐渐降低并趋于平缓, 而结合部与悬索段交接点竖向位移先上升后趋于平缓; 较大载荷分配比例下, 结合部刚度降低, 增设重叠吊杆导致结合部长度增加, 反而会增大竖向位移幅值, 不利于主梁平顺过渡.

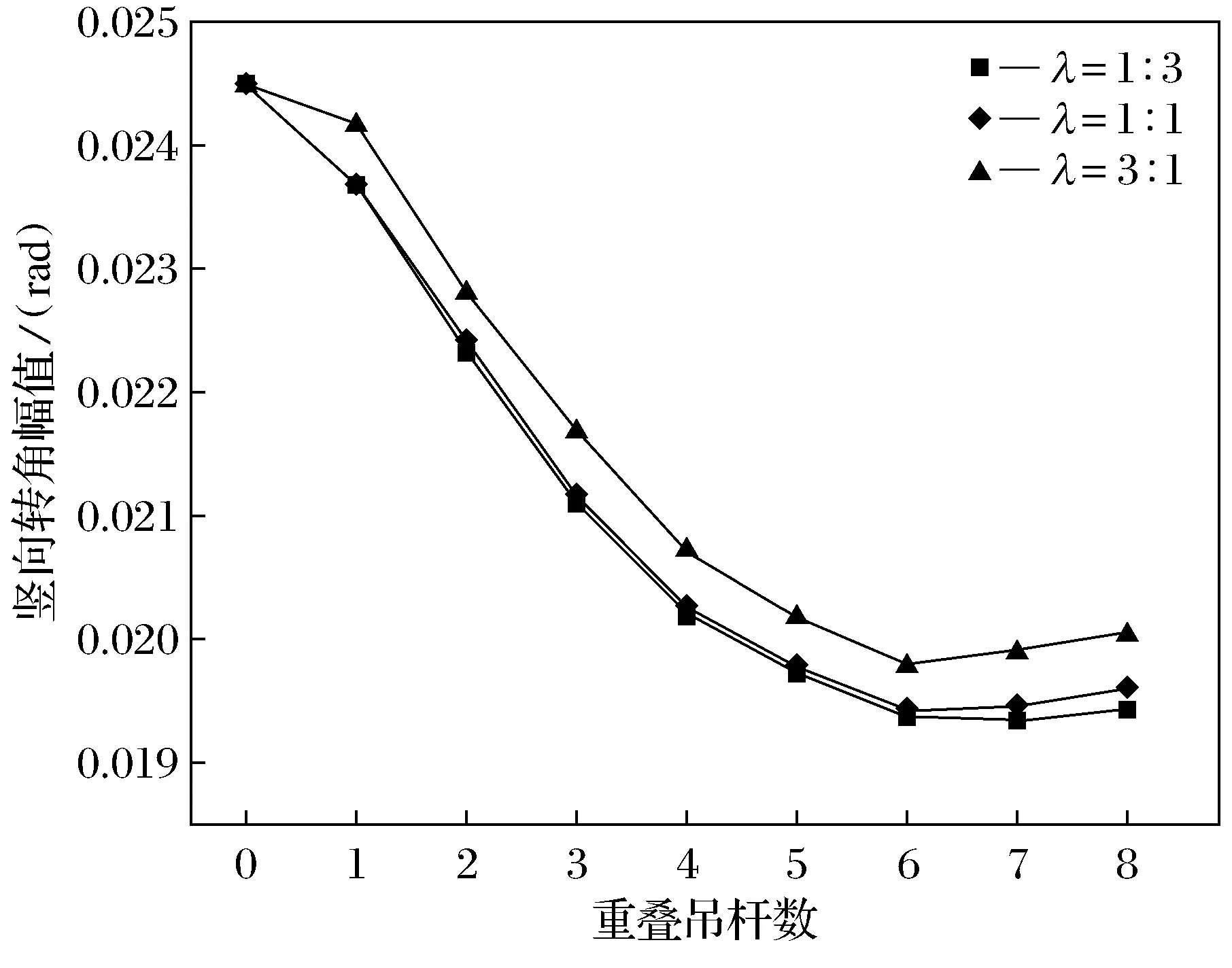
图13 结合部与悬索段交接点竖向转角幅值

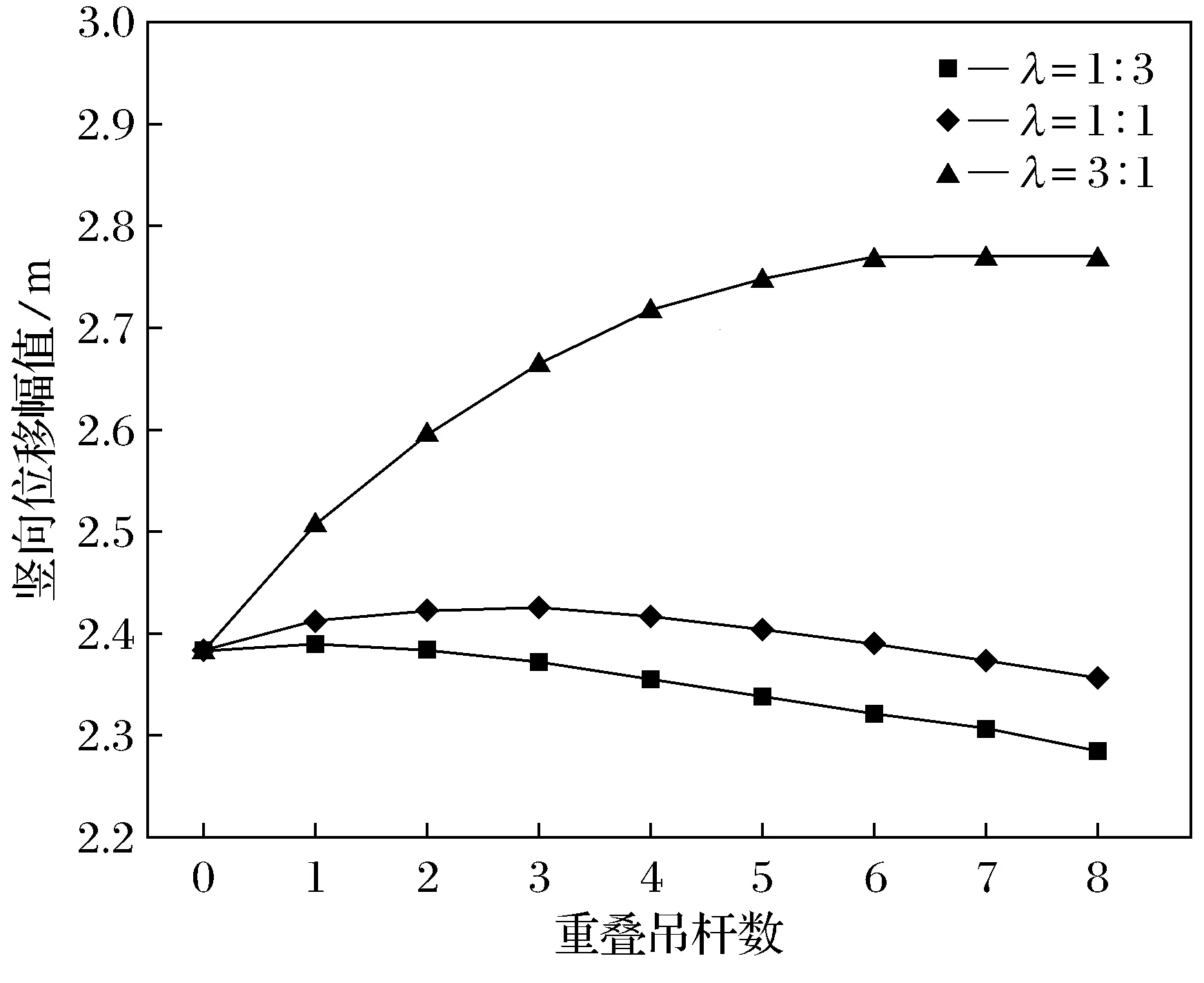
图14 结合部与悬索段交接点竖向位移幅值

4 结 论

本文对公铁两用吊拉组合体系桥结合部进行了参数分析,主要分析了重叠吊杆数和载荷分配比例2个主要参数对结合部的应力幅和位移幅的影响,结论如下:

1) 设置重叠吊杆可以明显降低悬索段端吊杆应力幅,同时设置重叠吊杆还可以使悬索段向斜拉段平顺过渡;

2) 由于主缆在斜拉段为无吊杆段,结合部重叠端吊杆应力幅高于其他重叠吊杆,其应力幅随着重叠吊杆数的增加呈现先上升后下降的趋势,设计过程应该考虑这一问题;

3) 结合部载荷分配比例λ取1∶3或1∶1为宜,计算发现λ取3∶1时,分配比例取值过高,容易造成结合部刚度降低,主梁过渡不平顺,增设重叠吊杆导致结合部长度增加,反而会加剧主梁过渡不平顺的现象.