单幅图像距离信息分析模型

徐宗煌, 林志强, 许美燕, 黄方方

(福州理工学院 a. 应用科学与工程学院, b. 计算与信息科学学院, 福建 福州 350506)

从图像或视频中提取物体的大小、距离、速度等信息是视觉情报分析工作的重要内容之一.在当前很热门的移动机器人[1]、无人驾驶[2]、计算机视觉[3]、无人机侦察[4-6]等领域,更是存在着大量的应用需求.

现阶段,国内外对单幅图像距离信息的分析研究已经日益成熟.袁海根[7]利用智能视觉图像技术,通过对运动目标与道路参考平面所在垂直、倾斜直线的交点,确定运动目标的空间位置.李泳波[8]基于机器视觉的RANSAC算法,通过提取每一帧城市复杂道路的视频单帧图像中的消失点平行线,提出了一种具有快速性、准确性、实时性以及良好鲁棒性的图像道路消失点检测算法.何立新[9]通过分析国内外有关视差测距的研究现状,提出了利用所采集的运动目标的多帧图像,通过运动估计法得到目标的运动视差信息.黄军等[10]通过介绍国内外有关单幅图像单目深度估计的模型方法,对单幅图像的深度估计的经典问题与进展进行了一系列的回顾和综述,同时总结了各个模型的稳定性和鲁棒性.傅思勇等[11]提出了一种综合相机透镜多畸变因素的相机标定方法,通过建立相机透镜多畸变模型,再以透镜的单应性为约束,利用相机透镜的投影原理获取相机内外参数.李婵[12]通过简化不同场景下的相机模型,接着检测运动目标标志物,并采用霍夫变换法获取运动目标所在道路方向上的消失点,最后基于VVH等相机自动标定算法与消失点相互匹配的模型得到相机的内外参数.此外,Zhe等[13]利用摄像机投影原理建立运动目标的面积距离几何模型,提出了一种基于3D检测的单目视觉端到运动目标距离的估计方法,该模型具有较高的准确性和鲁棒性.

本文基于RANSAC算法的双消失点法和相机投影模型,建立了单幅图像距离信息分析模型,得到了运动目标之间以及拍照者距地物目标的距离.该方法可简单而有效地提取视觉情报中地物目标的几何尺寸.

1 研究思路

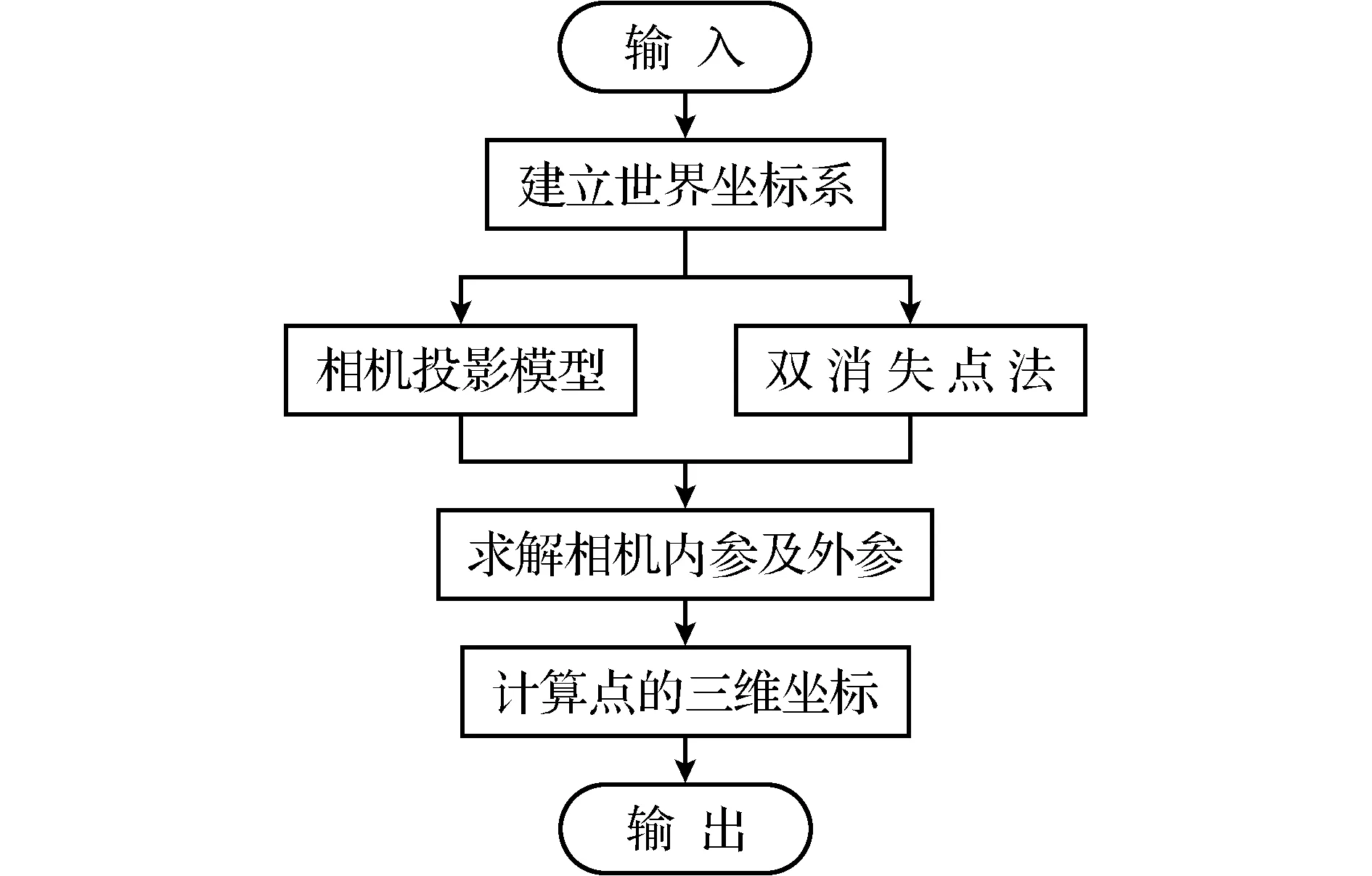
图1 单幅图像距离信息分析模型处理Fig.1 The processing of the distance information analysis model of a single image

在问题求解过程中,考虑到实际情况与简化计算的需要,提出以下相关的假设:①模型中所涉及的摄像机均不存在径向畸变和切向畸变;②相机光圈中心成像位于图片中心;③求解马路面上物体间距时,忽略人行道相对于路面的高度.

针对单幅图像的距离信息分析:①选择双消失点法计算相机内参数矩阵与外参数矩阵;②根据相机投影模型,在投影变换中存在3个坐标系,分别为像素坐标系、相机坐标系和世界坐标系;③在给定图片时,可以建立合适的坐标系,可知此时图片中某点在像素坐标系中的二维坐标;④依据上述已知条件,计算该点在世界坐标系中的三维坐标.图1所示为单幅图像距离信息分析思路.

2 单幅图像距离信息分析模型

2.1 相机投影模型

根据相机投影模型[7],相机将三维世界中的坐标点映射到二维图像平面的过程可以用几何模型进行描述.该几何模型有很多种,其中最简单的称为小孔模型[8],如图2所示.小孔模型是很常用而且有效的模型,它描述了一束光线通过小孔之后,在小孔背面投影成像的关系.

图2 小孔成像模型Fig.2 Small hole imaging model

小孔成像模型利用一个小孔和一个成像平面描述相机,小孔位于成像平面和实际的三维场景之间,任何来自实际场景中的光线只有通过小孔成像平面才能在成像平面中成像.因此,在成像平面和通过小孔看到的实际的三维场景中存在着一定的对应关系,即图像中的二维像素点与实际场景中的三维点存在某种变换关系.利用这种变换关系,就可通过图像中已知的二维信息恢复场景中某点的三维信息.

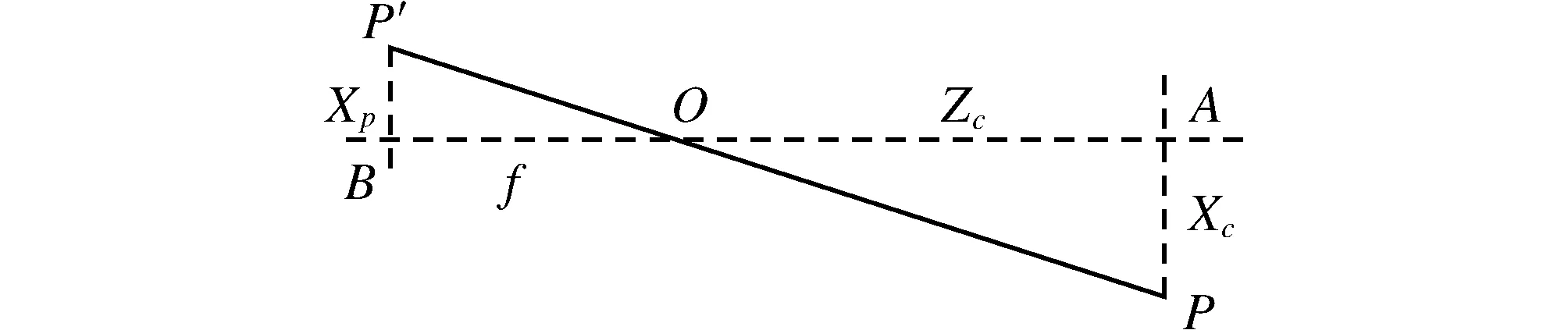
图3 成像相似三角形Fig.3 Imaging similar triangles

假设三维空间中有一点P,其在像素坐标系下的坐标是P′=[u,v],在图像坐标系中的坐标是Pp=[Xp,Yp,Zp]T,在相机坐标系中的坐标是Pc=[Xc,Yc,Zc]T,其中Zp=f,为相机焦距,在世界坐标系中的坐标是Pw=[Xw,Yw,Zw]T,如图3所示.

由图3中三角形的相似关系,可以得到

(1)

在二维图像坐标系中,像素坐标系(二维)原点位于图像左上角,因此,像素坐标系与成像平面存在缩放变换和平移变换.假设成像平面在x轴上缩放了α倍,在y轴上缩放了β倍,原点平移量为[cx,cy]T,那么,P点在相机坐标系中的坐标与像素坐标[u,v]T的关系为

(2)

将式(1)代入式(2),并令αf=fx,βf=fy得

(3)

式中,f的单位为m,α,β的单位为像素/m,所以fx,fy的单位为像素.将式(3)化为齐次坐标的形式得到

(4)

式中,3×3维矩阵K即为相机的内参数矩阵,P点坐标为相机坐标系下的坐标值.在一般情况下,相机坐标系相对于世界坐标系的关系可以通过旋转矩阵R和平移矩阵T来描述,即

Pc=RPw+T.

(5)

将式(5)代入式(4)可得

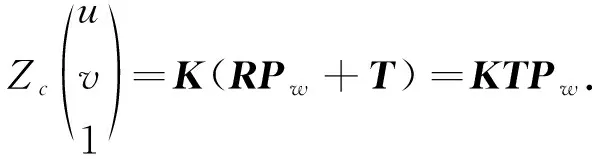
(6)

式(6)描述了某点在像素坐标系下的坐标P′=[u,v]与世界坐标系下的坐标Pw=[Xw,Yw,Zw]T的转换关系式.

2.2 基于双消失点的相机标定算法

本文采用基于双消失点相机的标定方法[14-16],该方法只要求图像中存在2组以上相互正交的平行线,大大简化了实际操作步骤.由于相机成像满足透视原理,因此空间上2条平行线在成像平面上的投影会在图像上有一个交点,称为消失点.且消失点的图像坐标只与对应空间直线的方向矢量有关,而且三维空间中互相平行的一组直线有且只有一个消失点FD.消失点具有以下4个属性:

图4 消失点法示意图Fig.4 Schematic diagram of vanishing point method

1) 相机光心与消失点的连线与形成该消失点的空间平行线平行;

2) 相机坐标系下,与空间3条两两正交直线形成的消失点相关的单位向量也两两正交;

3) 空间3条两两正交的直线形成的消失点组成的三角形,其垂心即为相机光轴与成像平面的交点(投影中心);

4) 消失点的坐标变换与平移向量无关,仅与旋转矩阵有关.

在基于双消失点理论计算相机参数时,要求拍摄的场景图片中可以找到2组相互正交的平行线,且与成像平面不平行.设从中提取出2组直线构成空间矩阵ABCD,它在图像中的投影为abcd,则图像中包含2个消失点,Fn是直线ad和bc构成的消失点,Fm是直线ab和cd构成的消失点,其示意图如图4所示.

为了避免2条平行线构成消失点带来的误差,本文通过检测多条平行线,利用RANSAC算法[17]对多条平行线构成的消失点坐标进行求解,得到最佳的消失点像素坐标p,其步骤如下.

输入:图像中若干条直线.

输出:消失点像素坐标p.

Step 1 从直线中随机选择k条直线,

Step 2 计算k条直线交于一点p′的最小二乘解,

Step 3 计算p′到所有直线的距离之和d,记录当d最小时的像素坐标p,

Step 4 重复Step 1,2,3,直至超过最大迭代次数或d小于设定阈值.

2.3 求解相机内参及外参数矩阵

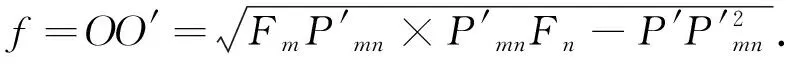
(7)

假设图像的cx,cy为图像长宽w,h的一半,且x和y方向上的焦距相等,即fx=fy=f,则可确定此时的相机内参矩阵K为

(8)

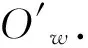
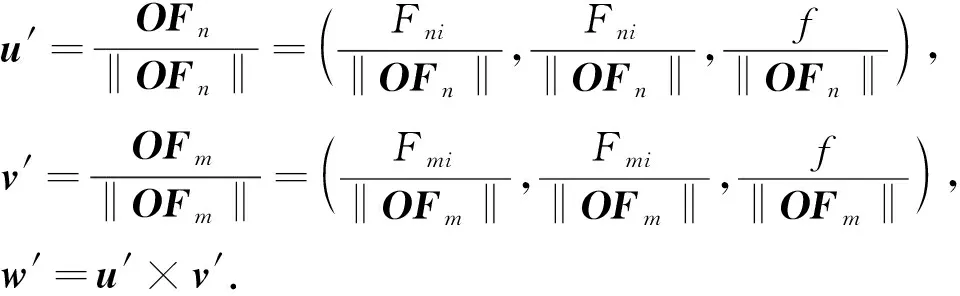
(9)

(10)

此时,已求得相机内参K,外参矩阵中的旋转矩阵R,接下来求解平移矩阵T.根据相机投影模型,有

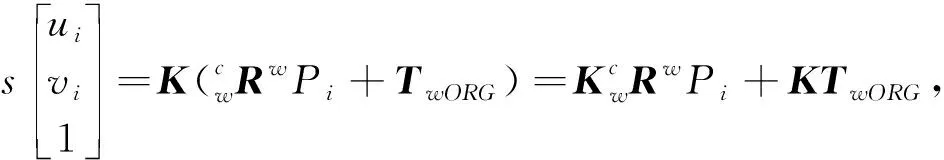
(11)

记

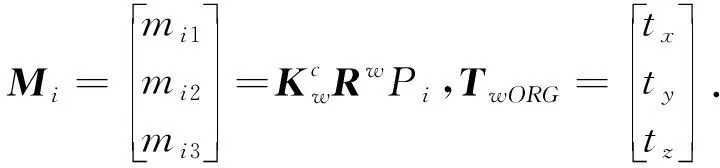
(12)

则可将式(11)改写为

(13)

展开得到如下方程组:

(14)

消去尺度参数s,并将式(14)改写为如下形式

(15)

求解式(15)的最小二乘解,即可求得平移矩阵T.

2.4 求解图像中点在三维空间中的坐标

由以上分析可知,相机坐标系原点在世界坐标系中位置为

(16)

考虑到某个空间点P,它的齐次坐标为P=(wPX,wPY,wPZ,1)T,在图像中投影到特征点x1=(u1,v1,1)T.此时定义增广矩阵[RT]为一个3×4的矩阵,其中包含坐标变换中的平移、旋转信息.因此,由上述推导可以得到

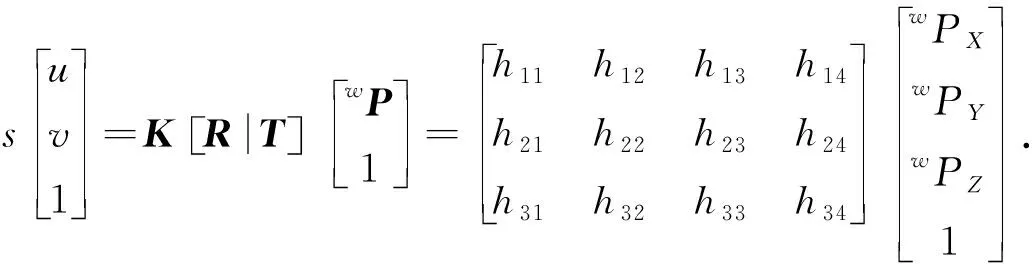
(17)

式(17)中含有3个待求解的未知数wPX,wPY,wPZ,2个约束条件.为求解该方程需添加一个约束条件.本文中选取约束条件为空间中某点P在世界坐标系中的wPZ值,假设该条件已知,因此有

(18)

求解该式即可得到wPX和wPY的值.即可求得点P在世界坐标系的坐标.

3 模型求解

3.1例1

要求测算出图5(见封3)中红色车辆车头A和白色车辆车头B之间的距离,以及拍照者距马路左侧边界的距离.首先建立世界坐标系Ow,图中红色表示坐标轴,黄色表示待求2点之间的距离.蓝线表示三维世界中的平行线,根据透视原理可知,这些平行线会交于一点,即消失点.接着使用Base点来计算含有准确尺度信息的外参数.故应选择在世界坐标系下已知坐标的点作为Base点.

1) 求解A、B两点之间的距离.

设A、B两点在世界坐标系下的坐标分别为

因此,计算可得A、B点之间的距离为

2) 求解拍照者距离左侧马路的距离.

马路左侧为远离拍摄者一侧的马路,即图5中E点所在的一侧.E点为在图像中马路左侧边沿任意选择的一点,设其在世界坐标系下的坐标为

因此,估算得到拍照者距离马路左侧的距离约为

3.2例2

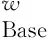
1) 求解A、C两点之间的距离.

设A、C两点在世界坐标系下的坐标分别为

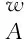
因此,计算可得A、C之间的距离为

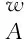
2) 求解拍照者与B的距离.

根据上一问求解所得B点坐标,可得

因此,估算得到拍照者与B的距离约为

4 结 语

本文提出了一种单幅图像距离信息分析模型,以实现视觉情报中地物目标的几何尺寸有效地提取.该方法通过建立合理的世界坐标系,基于RANSAC算法的双消失点法计算相机内参数矩阵与外参数矩阵;再根据相机投影模型,求解图像中点在三维空间中的坐标;最后得到运动目标之间以及拍照者距地物目标的距离.结果表明:所建立的单幅图像距离信息分析模型可以有效地提取视觉情报中地物目标的几何尺寸,且该方法实现过程简单,具有很好的可行性.