基于薄板稳定问题的砌体墙板高厚比限值

蒋耀华, 倪玉双

(1. 中机国际工程设计研究院有限责任公司 医疗建筑设计研究所, 湖南 长沙 410007;2. 长沙理工大学 土木工程学院, 湖南 长沙 410114)

砌体结构中,墙体主要承受压力,除了进行承载力计算以确保安全外,还应使其在正常使用时具有良好的工作性能,应保证其稳定性.高厚比验算被认为是保证砌体结构稳定性的构造措施之一.在尚无明确的方法和规定计算墙体变形的情况下,可以认为高厚比是保证墙体正常使用极限状态的主要手段之一[1].我国现行《砌体结构设计规范》(GB 50003—2011)[2]主要通过控制高厚比来保证墙体的稳定性,但其中的允许高厚比限值的规定主要根据实践经验,缺乏相应的理论体系.随着墙体材料的革新和建筑结构形式的改变,新型墙体材料不断涌现,如文献[3-4]中提到的纤维混凝土与泡沫混凝土等,因此研究具有一定理论基础的墙体高厚比限值变得尤为重要.

国内有关专家和学者对砌体高厚比展开了很多研究工作.主要集中在以下3个方面:第1类是分析高厚比对墙体承载能力及破坏形式的影响,文献[5-6]分析了高厚比对墙体的破坏形式的影响,文献[7]分析了墙体倾斜时其高厚比与受压承载力的关系;第2类主要是对高厚比验算的相关研究,文献[8-10]从不同侧重点对高厚比的验算进行了研究;第3类是对高厚比限值的研究,不过这方面的研究工作很少,刘兴远等[11]指出现行砌体规范在高厚比限值计算中的一些不足,但是没有指出如何解决这些不足.赵成文等[12]将墙体简化为柱对砌体结构高厚比限值进行了研究,为后续研究提供了一定的基础.国外很少对高厚比展开专门的研究,主要将其作为影响墙体承载力的一个因素加以分析[13-18],没有对高厚比本身的验算或其限值等进行专门研究的文献.

基于以上研究,本文尝试建立具有一定理论基础的砌体墙高厚比限值的计算方法.砌体墙是由块体、竖向灰缝、水平灰缝组成的一种各向异性材料,混合结构房屋中,承受垂直于墙面的风载、水平地震作用和土压力及悬挂设备等平面外载荷的砌体墙,本质上相当于不同边界条件下承受横向载荷的竖向平板,砌体墙的厚度一般远小于墙体的其他两个尺寸,故可将其看成薄板.对于薄板的稳定问题,已经有一套较为完整的理论供参考,但是,薄板理论假定物体是均匀的,所以可以把由块体和砂浆组成的砌体墙进行匀质化,将各向异性非匀质的砌体墙转化成各向异性匀质体,再结合Kirchhoff假定,构建砌体墙的薄板模型,从而借助薄板稳定问题的研究方法来研究砌体墙的稳定问题.

1 砌体墙板的匀质化

砌体墙的匀质化过程如图1所示[19],其中的RVE(representative volume element)即为图1所示砌筑形式下砌体墙的匀质化单元.匀质化单元同时包括了块体、竖向灰缝和水平灰缝.关于砌体墙板匀质化的详细过程和弹性等效常数的计算及薄板模型的建立,笔者在文献[20-21]中已有详细论述,此处不再赘述.

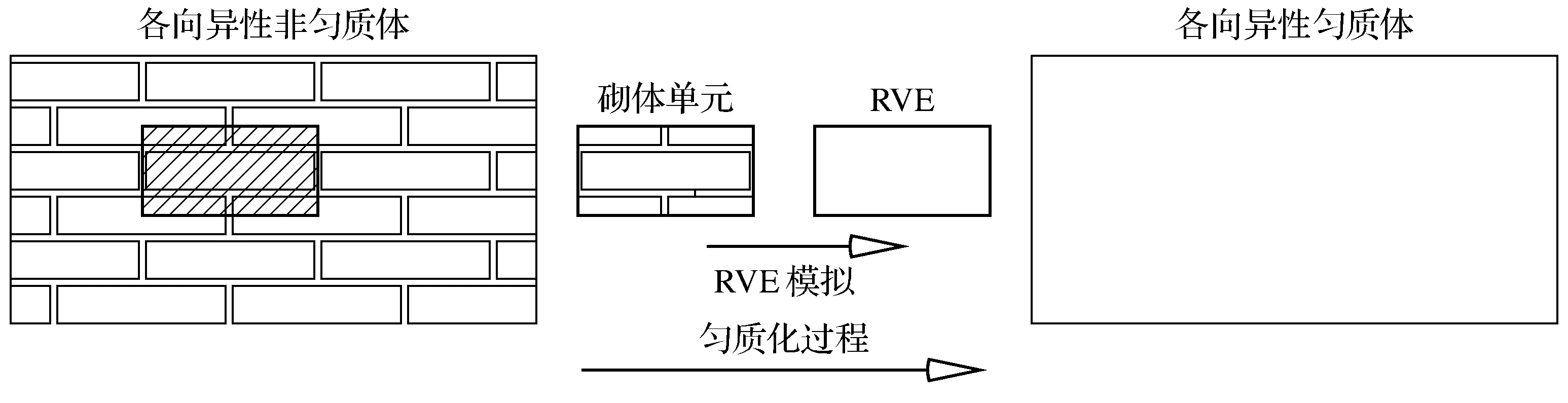
图1 砌体墙的匀质化过程Fig.1 Homogenization of masonry wall

匀质化后的砌体墙相当于正交各向异性薄板,可以运用薄板稳定理论来对其稳定性进行研究,即可以参照薄板的压曲来求解正交各向异性砌体墙板的压曲临界载荷,进而求出其高厚比限值.对于正交各向异性薄板而言,当四边简支或两对边简支的矩形薄板在简支边上受有均布纵向压力时,可以求得临界载荷的精确值.在其他情况下,可以用差分法或能量法求得临界载荷的近似值,计算步骤和各向同性板的情况相同.

本文以四边简支墙板为例,采用类比求各向同性薄板的压曲临界载荷的方法来求得匀质化后的正交各向异性砌体墙板的压曲临界载荷,为了便于将本文的研究成果推广到不同边界墙体,在求解压曲临界载荷时采用能量法.

2 四边简支墙板在均布压力下的压曲

2.1 各向同性薄板的压曲

从能量观点来看,压曲临界载荷可以由薄板从平面状态进入邻近的弯曲状态时,纵向载荷所做的功W等于形变势能Vε的增加的条件求得.即有如式(1)所示的功能方程

Vε-W=0.

(1)

2.1.1 纵向载荷所做功

图2为一四边简支,两对边受有均布载荷的匀质化砌体墙板.纵向载荷所做的功W可以按照载荷引起的中面内力所做的功来计算.设纵向载荷引起的墙板的中面内力为FTx、FTy、FTxy,则纵向载荷在压曲过程中所做的功

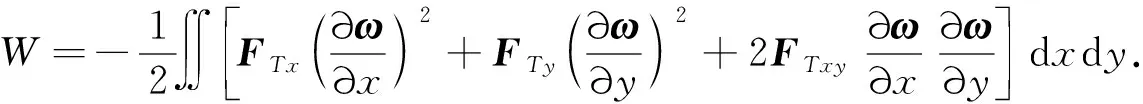
(2)

式中,ω为挠度,为了使得设定的挠度较好地符合临界载荷下的挠度,从而求得较精确的临界载荷,设定挠度的表达式为

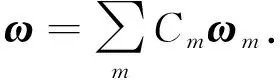
(3)

式中:ωm为满足位移边界条件的函数;Cm为互不依赖的待定系数,选择Cm时,可以应用最小势能原理.由最小势能原理及式(1)可知

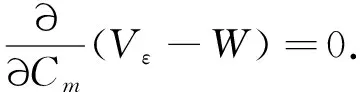
(4)

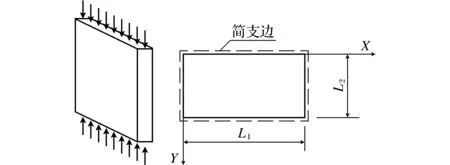
图2 墙板的边界条件和载荷形式Fig.2 Boundary conditions and load pattern of wall

式(4)将给出Cm的m个齐次线性方程.为了ω具有非零解,Cm就必须具有非零解,因而这个齐次线性方程组的系数行列式必须等于零.这样就得出求解临界载荷的方程.由此可见,要求解压曲临界载荷,还需求得压曲状态下墙板的形变势能Vε.

2.1.2 形变势能

在薄板的小挠度弯曲问题中,形变势能的表达式简化为[22]

(5)

式中:σx、σy、τxy为平面应力分量;εx、εy、γxy为平面应力对应的平面应变分量.可分别用挠度表示如下:

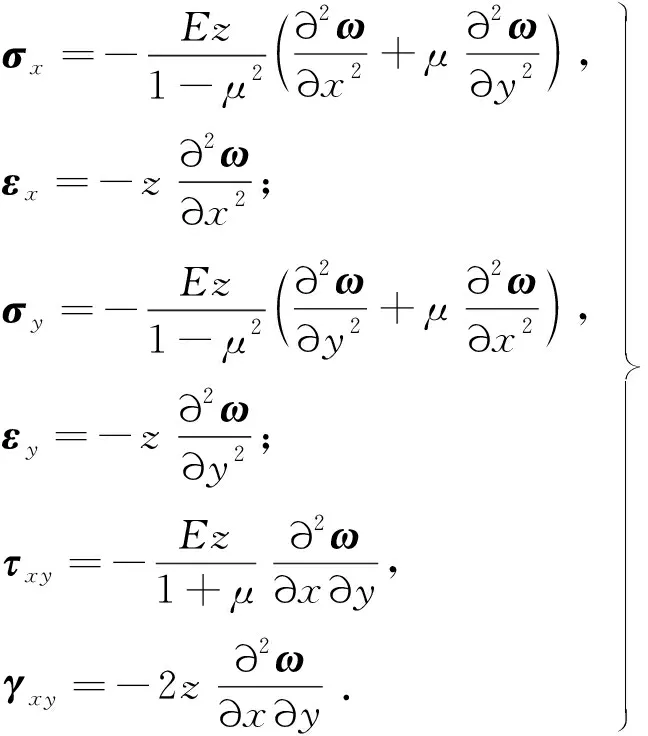
(6)

式中:E为弹性模量;μ为泊松比.将式(6)带入式(5),整理后得

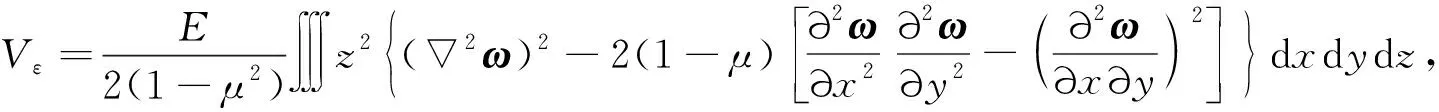
(7)

式中,

因为式(7)右边大括号中的各项都不随z而变,故可对z积分,并引入板的弯曲刚度D可得

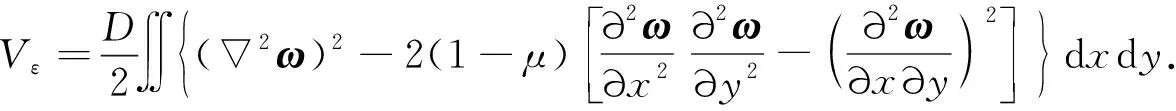
(8)

将式(8)改写为

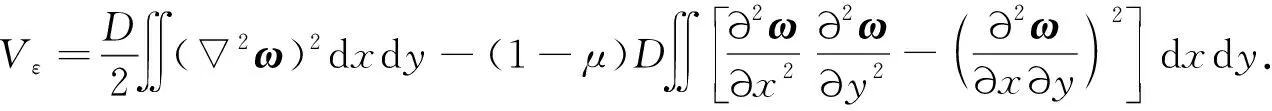
(9)

式(9)中的第二个积分可以变换为

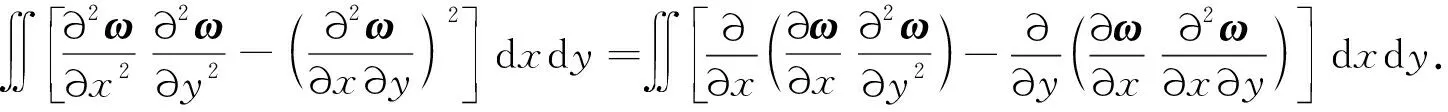
(10)

按照格林定理,有

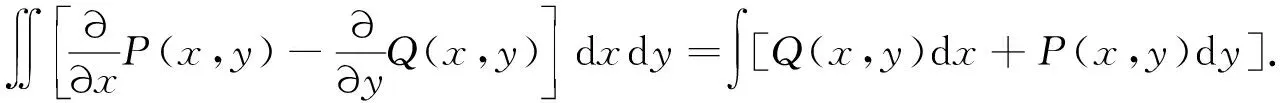
(11)

于是,式(10)可以写为

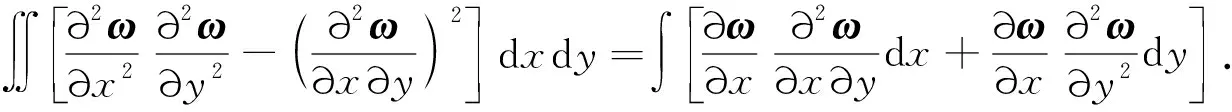
(12)

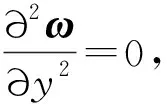
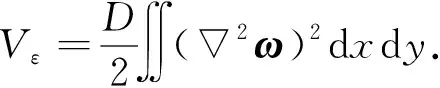
(13)

2.1.3 压曲临界载荷

墙板压曲以后的挠度ω的表达式可取为式(14)所示[22]:

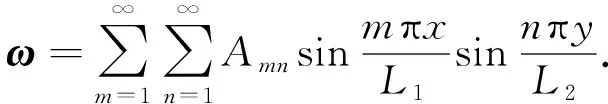
(14)

式中:Amn为某一系数,可通过对其求导后在方程中消除;m和n为任意正整数.将式(14)带入式(13)中,对x和y积分.对于图2中所示的砌体墙板,对x积分是从0到L1;对y积分是从0到L2,最后得到

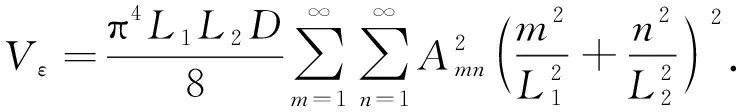
(15)

设图2所示的墙板在两对边受每单位长度为py的均布压力,则中面内力为FTx=0,FTy=-py,FTxy=0.联合式(14)带入式(2)可求得纵向载荷在压曲过程中所做的功,

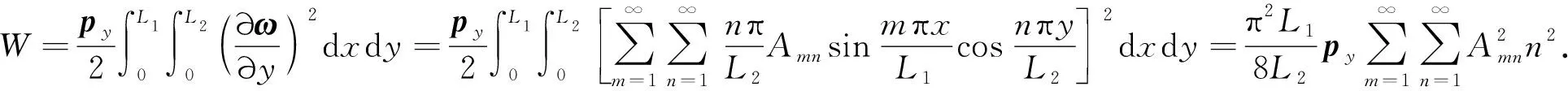
(16)

式(4)在这里成为

将式(15)和式(16)代入,得出

令这一方程的系数行列式(即方程的唯一系数)等于零,即得压曲临界载荷

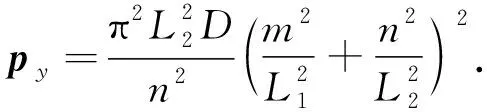
(18)

2.2 正交各向异性砌体墙板的压曲

用能量法求正交各向异性砌体墙板的压曲临界载荷时,计算步骤和各向同性板相同.

类比式(13)可得正交各向异性墙板形变势能表达式

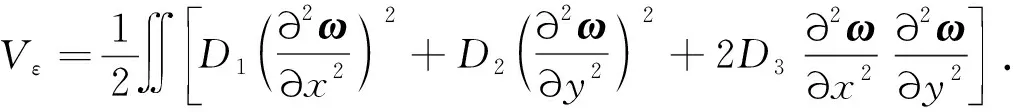
(19)

式中挠度ω的表达式仍然取式(14),D1、D2是薄板在弹性主向的弯曲刚度,D3为通过主刚度计算而得,计算公式均参看文献[21-22],将式(14)带入式(19),对x积分是从0到L1,对y积分是从0到L2,最后得到

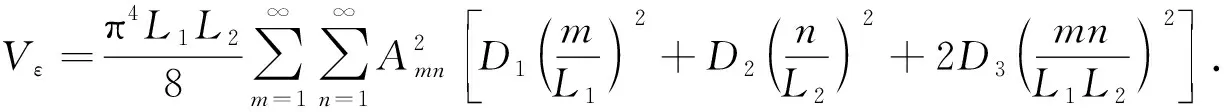
(20)

式中纵向载荷在压曲过程中所做的功仍然可用式(16)表示,式(4)仍然可以表示为

将式(16)和式(20)代入可得

(21)

由式(21)可得正交各向异性墙板的压曲临界载荷为

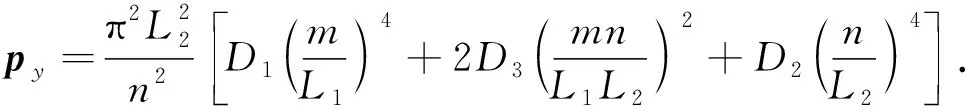
(22)

式(22)中,py随m增大而增大,故求临界载荷时,取m=1,则临界载荷

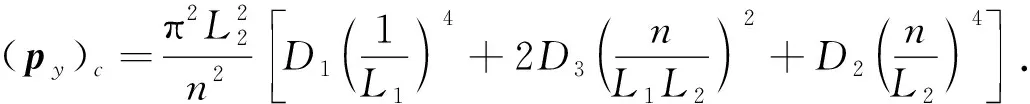
(23)

将式(23)变形为

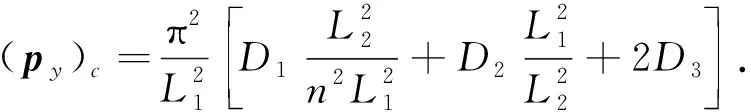
(24)

由式(24)可知,对于任何已知的比值L2/L1,都可以令n取不同的整数,求出不同的py值,从而得到最小的py值,即(py)c.

3 匀质化砌体墙板的高厚比限值计算

3.1 计算公式

取砌体墙的临界载荷(py)c=fmt,t为墙体厚度,fm为墙体抗压强度平均值,按现行砌体结构设计规范进行计算,式(24)可以变换为

(25)

令β=L2/t为墙体高厚比,ζ=L2/L1为墙体高宽比,则由式(25)可变形得到如式(26)所示的墙体高厚比限值的计算公式:

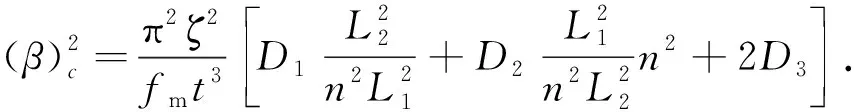
(26)

3.2 算 例

以由240 mm×115 mm×53 mm的烧结普通砖砌筑而成的240 mm厚墙体为例进行计算,墙体高宽比取1.0,本文公式中涉及的砖和砂浆的弹性模量及泊松比取值按文献[23]进行计算,竖向灰缝和水平灰缝均取10 mm,f1为块体的强度等级值,f2为砂浆强度等级,fm为砌体抗压强度平均值,匀质化墙板的高厚比限值计算结果见表1.

由表1中计算结果可知,计算高厚比限值平均值与规范值非常接近,验证了式(26)的适用性,且计算值略小于规范允许值,偏于安全.

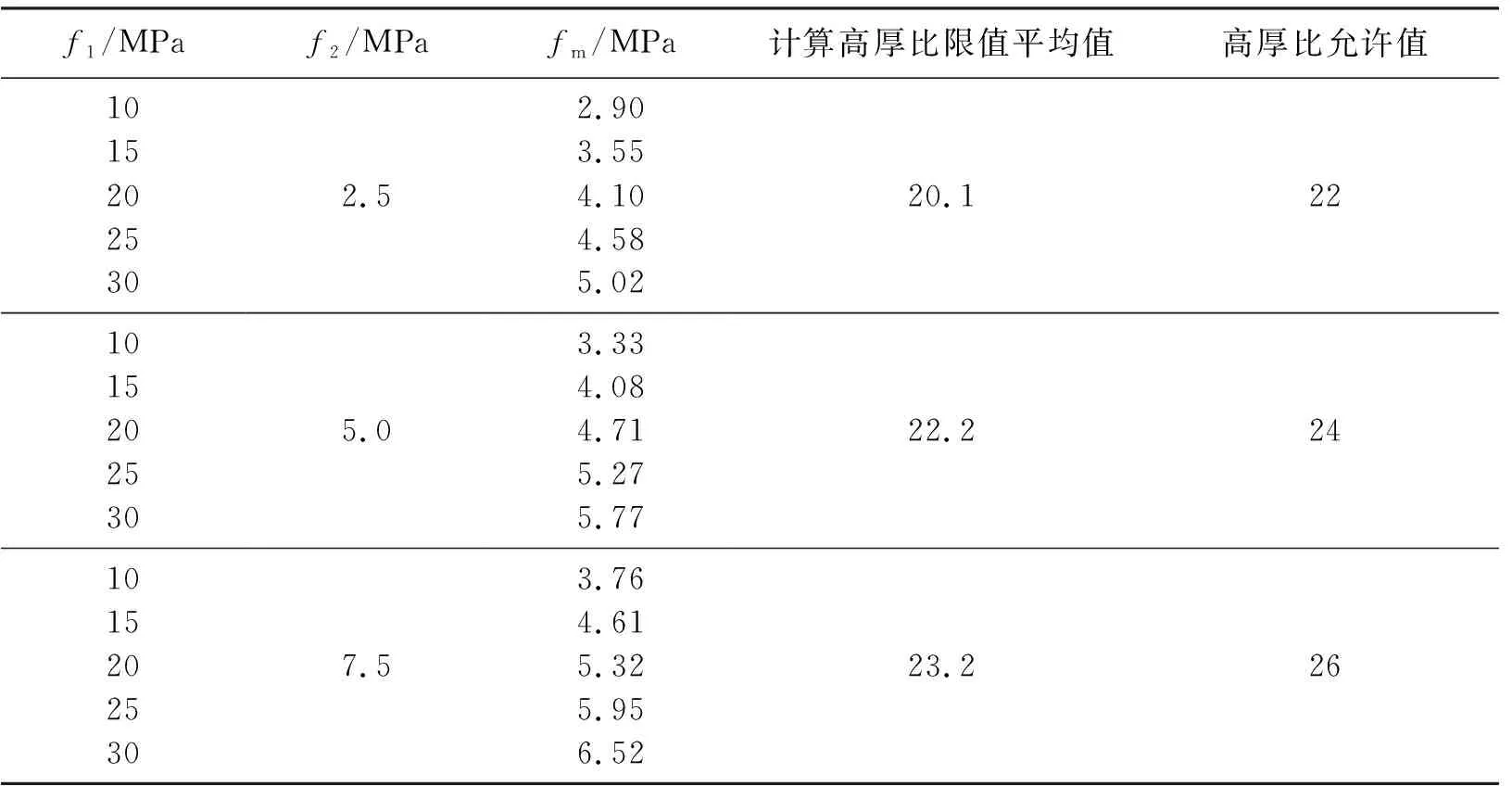
表1 匀质化墙板的高厚比限值比较Table 1 Comparison of limiting value of height-to-thickness ratio of homogenized wall

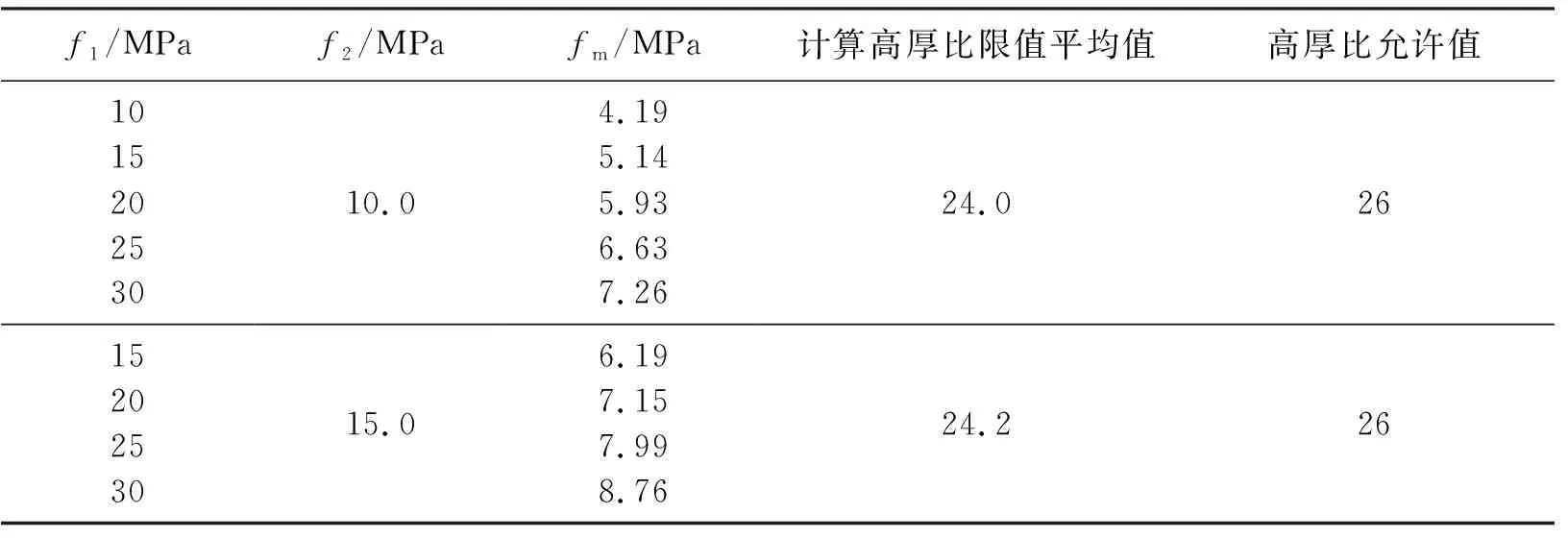
续表1

4 结 论

本文基于薄板的稳定问题来研究砌体墙的稳定性,得到的主要结论如下:

1) 将由块体和砂浆组成的砌体墙进行匀质化,即将各向异性非匀质的砌体墙转化成各向异性匀质体,利用已构建的砌体墙的薄板模型,借助薄板稳定问题的求解方法来研究砌体墙的稳定问题,能为砌体墙板的稳定性提出新的研究思路;

2) 通过与规范允许值比较可知,本文参照板的稳定问题求解得出匀质化后砌体墙板的压曲临界载荷,进而求得其高厚比限值的计算方法,力学概念清楚,安全可行;

3) 本文采用能量法求得匀质化砌体墙板的压曲临界载荷,可推广应用于不同的新型墙体材料和不同边界条件的墙体,为弥补现行规范中高厚比缺乏相应的理论体系和计算方法的不足提供了一种解决方法,具有一定的实用价值,可供后续研究及规范修编参考.