新型串行融合Reed-Solomon码译码器设计

安翔宇,梁煜,张为

(天津大学微电子学院,300072,天津)

里德-所罗门(Reed-Solomon,RS)码[1]是一种重要的差错控制码,因其纠错能力强、构造简单等,广泛应用于深空探测[2-3]、无线通信[4-5]、数据存储[6]等诸多领域,一直是学术界和产业界研究的重点与热点。RS码译码算法主要包括硬判决译码[7-10](HDD)和代数软判决译码[11-14](ASD)两大类。

目前,典型的HDD算法是在伯利坎普-梅西(BM)算法[2]基础上发展起来的改进的无逆伯利坎普-梅西(RiBM)算法[9]。与HDD算法相比,ASD算法充分运用信道软信息,具有更加优异的纠错性能。在现有的ASD算法中,低复杂度蔡斯(LCC)[11-12]算法是具有最低计算复杂度,硬件实现最为简单的算法。为了进一步提升LCC算法的速度、减小硬件实现面积,García-Herrero等提出了一种基于硬判决的软判决译码(HDD-LCC)算法[15-16],用HDD译码流程取代传统LCC算法中复杂的插值运算,通过求解测试向量并分别译码的思路提升纠错能力。

图1 流水线结构的融合RS码译码器架构

上述译码算法在高斯白噪声信道(AWGN)中表现出优异的性能。然而实际中的信道更接近于突发错误信道(Bursty),由于脉冲的干扰,时常出现码字连续出错的现象。连续突发错误很容易超出传统译码算法的纠错能力。针对这种特别出错形式,需要采用特殊的译码处理方式来提升译码性能。Wu等提出的擦除(BC)算法成为突发错误译码算法研究的基础[17],文献[18]提出基于该算法的改进无逆擦除(RiBC)算法。这类算法可以同时纠正β个随机错误和长度为f(f<2t-2β-1,t为RS码纠错能力)的单段突发错误,通过假设突发错误位置并迭代求解的方式实现译码。为适应不同信道的译码需求,胡岩等提出了一种结合随机错误译码与突发错误译码的RiBM-RiBC融合译码算法[19]。为进一步提升译码性能,Wang等将修正的RiBC算法(riBC)与软判决HDD-LCC算法结合,提出了一种针对突发错误的融合软判决译码算法BCHDD-LCC,并设计了一种流水线结构的融合RS码译码器,在有无突发错误时分别采用BCHDD-LCC算法及HDD-LCC算法译码[20-21]。此类融合译码器在译码随机错误与单段突发错误时均具有优异的译码性能,进一步拓宽了RS码译码器的应用范围,为自适应信道环境的RS码译码器设计提供了思路。

流水线结构的译码器每级延迟是固定的,其中存在大量的空闲等待时间,影响译码器的译码效率、降低硬件利用率,文献[22-25]中对此问题进行分析并提出了部分改进方案。在对流水线结构融合RS码译码器进行时序分析时,发现空闲等待时间的问题同样存在并值得优化。针对此,本文设计了一种同时适用于随机错误与单段突发错误译码的mSPCF模块,并提出了一种新型串行融合RS码译码器。实验结果表明,与流水线结构的融合译码器相比,本文提出的译码器具有更低的译码延时和更高的吞吐率,实际应用更具优势。

1 流水线结构融合译码器时序分析

流水线结构融合RS码译码器架构如图1所示。首先通过重数分配模块(MA)根据突发错误预判断机制[21,26]获取码字错误信息、码字η个最不可靠位置并得到2η个测试向量,该模块由软件实现。再由校验子计算(SC)模块得到第一个测试向量的校验子,其余校验子由校验子更新(SU)模块依次更新得到。关键方程求解(KES)模块根据错误信息选择riBC或RiBM算法,得到当前测试向量的错误值及错误位置多项式。多项式选择(PS)模块判断当前错误多项式能否译码成功,如果可以,则无需执行后续测试向量。最终,钱搜索和福尼算法模块(CSFA)根据错误多项式求得错误图样并完成译码。

流水线结构融合RS码译码器的时序关系如图2所示。SU、riBC&RiBM、PS这3个模块(简称SKP)处于同一级流水线阶段中,该译码器是由SC、SKP、CSFA模块组成的3级流水线结构。对于流水线结构,每级流水线阶段都是固定的,只有SC、SKP、CSFA模块都计算完成才能进入下一阶段的计算。

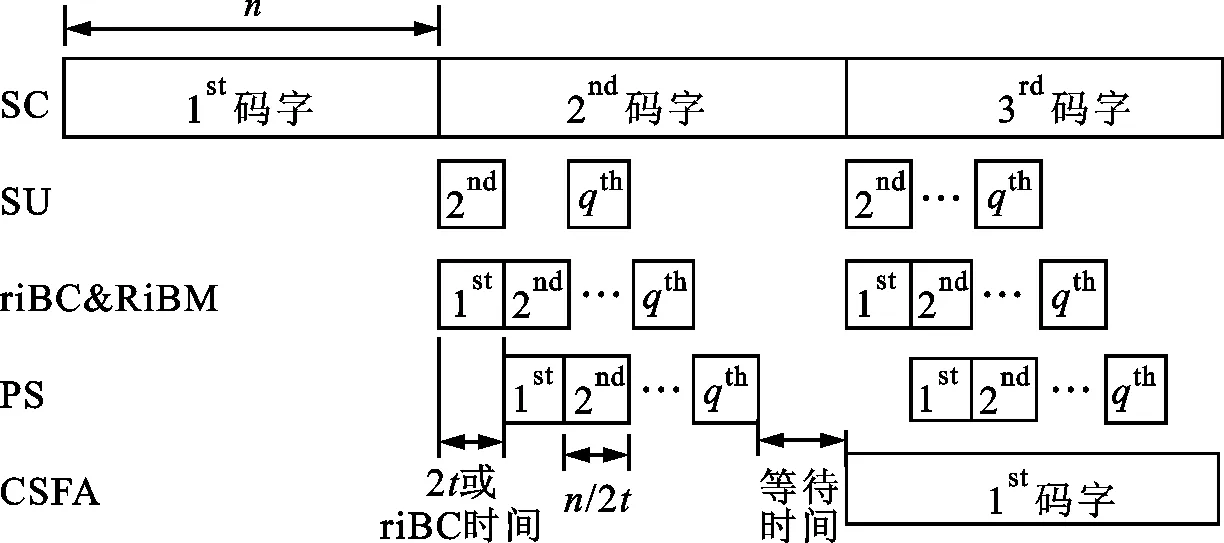
(a)总体时序关系

(b)riBC时序关系图2 流水线结构融合RS码译码器时序关系图

对于(n,k)RS码,其纠错能力t=(n-k)/2。SC、CSFA模块的译码延迟为n,SKP模块的译码延时根据码字情况变化。如果SKP模块译码时间小于n,则SKP必须经过一定的等待时间才能进行下一阶段的计算。

由于PS模块具有判断错误多项式并提前中断的功能,SKP只需执行q(1≤q≤2η)个测试向量。SU模块与PS模块的计算时间分别为2t、n/2t。根据MA模块得到的错误信息,riBC&RiBM模块将选择不同关键方程求解算法:译码随机错误时,采用RiBM求解算法,计算时间为2t;译码单段突发错误时,采用riBC求解算法,计算时间与突发错误位置测试数L密切相关,如图2b所示。特殊的,融合译码器没有译码多段突发错误的能力,在错误信息判断后译码器直接输出,以下不予讨论。

用TSKP_random、TSKP_burst分别代表译码随机错误、单段突发错误时的SKP计算时间,假设此时执行测试向量数为q、突发错误位置测试数为L,tlarger为2t、n/2t中的较大值,则SKP计算时间可分别表示为

TSKP_random=2t+qtlarger

(1)

(2)

为了更直观地分析SKP译码时间,对(255,239)RS码译码时的q、L进行概率分布测试。随机错误由高斯信道产生,单段突发错误由基于马尔可夫链的突发错误信道模型[20]产生。

图3是在η=3、信噪比(SNR)为6.2 dB的条件下,随机错误译码的执行测试向量数q的概率分布,译码器有90%以上概率只执行第1个测试向量,根据式(1),此时SKP仅需要32个时钟周期。即使在译码器需执行所有8个测试向量的情况下,SKP也只需要144个时钟周期,均远小于SC、CSFA执行用的255个时钟周期。因此,在译码随机错误时第2级流水阶段SKP中存在大量空闲等待时间。

图3 随机错误译码执行测试向量数的概率分布

在η=3、β=2,信噪比为6.2 dB的条件下,进行单段突发错误译码的概率分布测试,结果如图4所示。由图4a所示,所有的单段突发错误均成功实现译码,且执行测试向量数q的平均值为1.015。突发错误位置测试数L的概率分布如图4b所示,L集中分布在4～7之间,平均值为5.499。根据式(2)可知,粗略计算SKP的平均译码时间为(13×5.499+11)×1.015+16=99.724,此值仍均远小于SC、CSFA执行用的255个时钟周期。

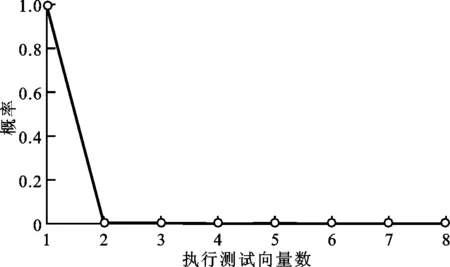
(a)执行测试向量数的概率分布

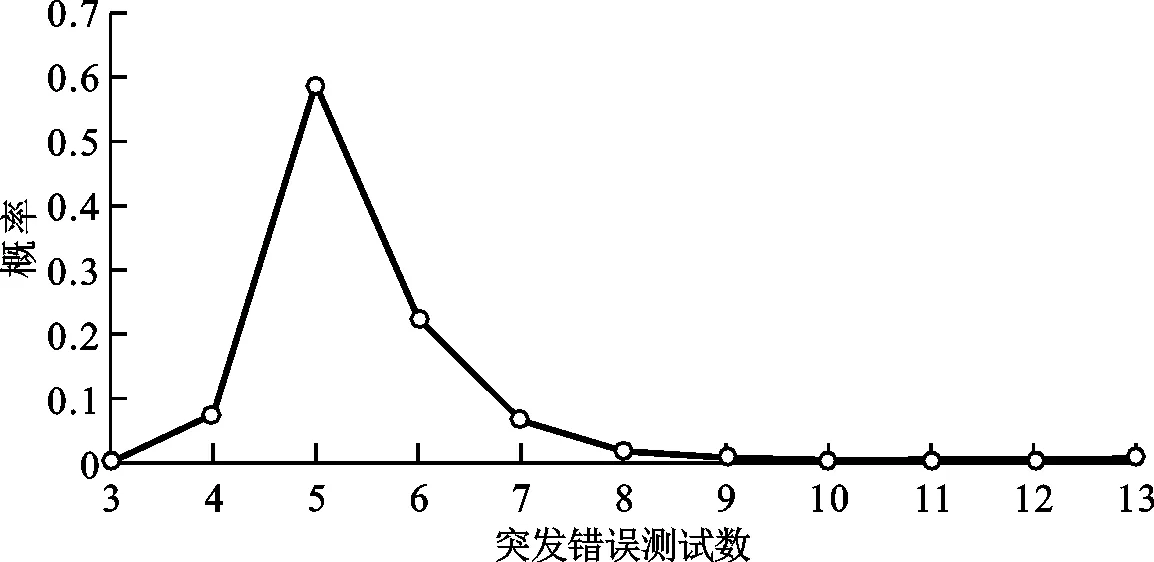
(b)riBC模块突发错误位置测试数的概率分布图4 单段突发错误译码的概率分布情况

2 新型串行融合RS码译码器

流水线结构的融合译码器在译码随机错误及单段突发错误时,第2级流水阶段SKP中均存在大量空闲等待时间,非常影响译码效率。调整译码过程时序关系,设计新型串行融合RS码译码器将能有效消除等待时间,大大减少译码器的译码延时。

文献[25]提出了一种串行高效LCC译码器,并设计了一个并行的校验子计算-多项式选择-钱搜索-福尼算法(SPCF)模块,在不同时间分别实现SC、PS、CS和FA模块功能,大幅提升了传统LCC译码器的译码速度及吞吐率。该译码器只适用于随机错误译码,无法适应复杂的信道环境。因此,在原始SPCF模块的基础上,提出了一个能适用于融合译码器的修正的SPCF模块(mSPCF),并设计了一种新型串行融合RS码译码器。与原始SPCF模块相比,所提出的mSPCF模块能用于纠正随机错误及单段突发错误,并具有更低的译码延时。

图5 mSPCF模块的电路结构

根据译码各模块功能及运算过程,PS模块判断当前错误多项式能否译码成功,此功能通过检查错误位置多项式的阶数与根的个数是否相等实现。CS模块将所有码元位置依次代入错误位置多项式并检查值是否为0,来搜索错误位置多项式的全部根,得到错误位置。PS和CS模块针对错误位置多项式根的运算与判断,无需重复进行。所提mSPCF模块将原始SPCF模块中分步进行PS、CS的过程修正为PS、CS模块同时进行。

SC模块计算2t个校验子Si。令r0～rn-1为码字的全部码元,α0～αn-1为码元的全部位置,α为(n,k)RS码本原元。将SC模块设计为p度并行,则其计算公式可以整理为

Si=

(3)

PS/CS模块搜索到错误位置多项式的全部根,同时判断该错误多项式能否译码成功。如果能成功,则由FA模块求解错误值。令关键方程求解模块得到的错误位置多项式σ(x)的系数为σ0～σe,错误值多项式ω(x)的系数为ω0～ωe-1,σodd(x)是σ(x)的奇数项,E(x)是最终的错误值。PS/CS、FA模块的计算式为

σ(αi)=σ0+σ1αi+…+σe(αi)e,0≤i≤n-1

(4)

0≤i≤n-1

(5)

式中:在译码随机错误与单段突发错误时,e的值分别为t与2t-β。

可以看出,式(3)～(5)都在求解特定多项式的根,计算过程的电路可以较好地兼容。基于此,设计mSPCF模块电路结构(见图5)。mSPCF模块最下面一行的选择器在不同时间分别选择系数r0～rn-1、σ0～σe、ω0～ωe-1来执行SC、PS/CS、FA模块功能。mSPCF模块的每一个基本单元(实线框)计算多项式的一项。为了能够同时纠正随机错误及单段突发错误,mSPCF模块的基本单元共2t(2t-β)个。

在进行式(4)、式(5)的PS/CS或FA模块运算时,需要对全部n个码元位置进行运算,共计n个多项式。如图5所示,mSPCF模块共2t行,每行计算一个多项式值,计算完所有多项式共需n/2t个计算周期。为方便FA模块的求解,σodd(αi)与σeven(αi)分开计算,并由求逆器求解σodd(αi)的倒数。如果码字错误为单段突发错误,每行所有2t-2β个基本单元均参与运算。如果码字错误为随机错误,则只有虚线框内的2t个基本单元参与运算。

此外,在高斯信道环境下,随着信噪比增大,会出现越来越多的无错误情况,此时2t个校验子全为0。对无错误的情况继续进行错误多项式的求解过程,将会造成不必要的时间及资源消耗。因此,在mSPCF模块新增了一个校验子判断环节。如果校验子计算后结果全为0,说明码字无错误,直接将全部输入码字输出。否则,仍需依次通过SU、riBC& RiBM、PS、CS、FA过程求解错误图样最终完成译码。此判断只需增加极少的硬件资源消耗,却在信道环境较好的情况下大幅降低译码器延时。

基于所设计的mSPCF模块,提出了一种新型串行融合RS码译码器,架构如图6所示。mSPCF模块在不同时间分别实现SC、PS/CS、FA模块功能,因此串行融合译码器只需MA、mSPCF、SU、riBC&RiBM模块即可实现译码。

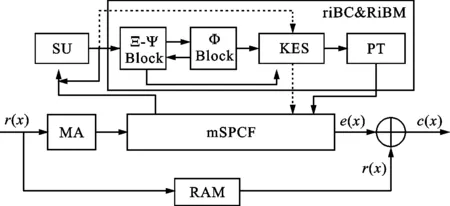
图6 新型串行融合RS码译码器架构

3 新型串行融合译码器性能分析

3.1 延时分析

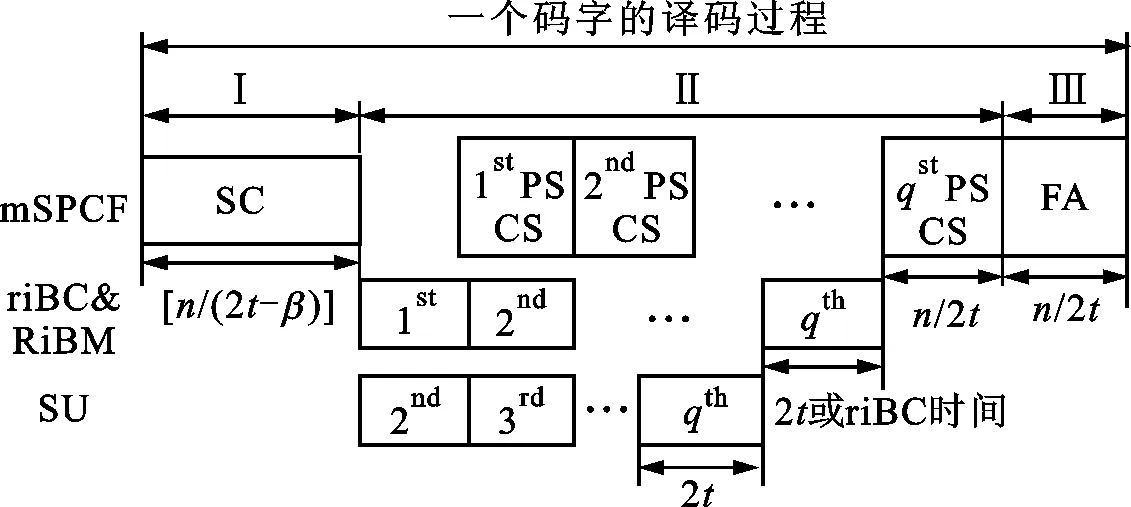
图7 新型串行融合RS码译码器时序关系

在译码码字无错误时,译码器只需进行SC模块并以2t度并行输出,此时译码器译码延时为

(6)

在码字错误为随机错误时,SKP计算时间同式(1),此时译码器译码延时为

(7)

在码字错误为单段突发错误时,SKP计算时间同式(2),此时译码器译码延时Tq,burst为

Tq,brust=

(8)

该译码器在高斯信道及突发错误信道(考虑所有码字均含单段突发错误)的平均延时计算式为

(9)

(10)

式中:pq,random、pq,burst分别表示译码随机错误及单段突发错误时执行q个测试向量的概率,pr表示码字无错误的概率,概率大小与信道环境密切相关。

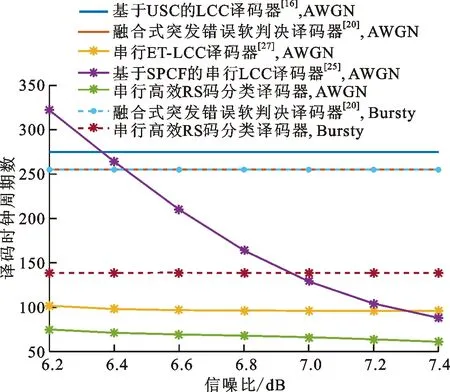
图8 不同译码器的延时对比

图8给出在RS(255,239)、η=3、β=2条件下串行融合译码器的译码延时,并与基于USC的LCC译码器[16]、流水线结构融合译码器[20]、串行ET-LCC译码器[27]、基于SPCF的串行LCC译码器[25]对比。其中,实线是高斯信道下的译码延时情况,虚线是突发错误信道且每个码字均含单段突发错误时的译码延时情况。可以看出,在高斯信道下,串行融合译码器具有最低的译码延时,且随着信噪比的增大不断下降。在信噪比6.2～7.4 dB范围内时,所提译码器的平均延时相比文献[16]、[20]、[27]、[35]中译码器可分别减少75.38%、73.45%、63.01%、29.68%。此外,在突发错误信道下,信噪比变化影响的是码字含单段突发错误的概率。当仅对单段突发错误进行测试时,其译码延时基本不随信道信噪比变化,且比流水线结构译码器的平均延时减少了45.65%。

3.2 硬件实现结果

本文提出的新型串行融合译码器在RS(255,239)、η=3、β=2的条件下实现了Verilog HDL建模,并在SMIC 0.13μm CMOS工艺下采用Design Compiler工具实现了逻辑综合。考虑到同时具有纠正随机错误与单段突发错误的能力,表1给出了流水线结构融合译码器及所提串行架构融合译码器的综合结果对比(综合工具及工艺保持一致)。

新型串行融合RS码译码器的面积为0.447 mm2,需要37 620个二进制异或门,相比流水线结构减少约9.4%的硬件资源消耗。串行融合译码器的最大时钟频率为187 MHz,相比流水线结构有所下降。信噪比在6.2～7.4 dB范围内的高斯信道下,串行融合译码器平均延时约为67.7,吞吐率达5 634 Mb/s,相比流水线结构增加约236.76%。在仅含单段突发错误的突发错误信道下,串行融合译码器的平均延时约为138.6,吞吐率达2 752 Mb/s,相比流水线结构增加约64.49%。

表1 RS(255,239)融合译码器实现结果

4 结 论

本文分析流水线结构融合译码器的时序关系,发现其第2级流水阶段存在大量空闲等待时间。为消除该等待时间、提升译码效率,本文提出了一种新型串行融合RS码译码器,并设计了修正的SPCF模块。本文进行了串行融合译码器的译码延时分析,与其他多种译码器对比,所提译码器均取得了一定的延时优势。串行融合译码器通过Design Compiler工具在SMIC 0.13μm CMOS工艺下实现,与流水线结构相比,所提串行结构可减少约9.4%的硬件资源消耗,在高斯信道及突发错误信道下译码时,吞吐率可分别提升236.76%和64.49%。综上,本文所提具有融合纠错能力的串行融合译码器具有更为优异的性能。