介质阻挡放电涡发生器等离子体激励条件下壁面气膜冷却性能研究
2021-03-08黄悦峰张子寒何坤晏鑫
黄悦峰,张子寒,何坤,晏鑫
(西安交通大学能源与动力工程学院,710049,西安)
提高透平进口燃气温度,是提升燃气轮机热效率和装置比功的一种行之有效的方法。然而,透平叶表热负荷随进口燃气温度逐步提升而不断增大,亟需采取先进的冷却技术增强高温叶片的热防护效能。早期研究发现,平板壁面自由射流的涡系由马蹄涡、剪切层涡、尾迹涡及肾形涡对等流场结构组成[1]。其中,肾形涡对能将热气流下拉至壁面附近区域,并使湍流扩散边界附近的冷气流向远离壁面的方向抬升[2]。所以,提升壁面冷却性能的关键在于利用流动控制技术抑制肾形涡对结构的发展[3]。
为了达到抑制下游区域内肾形涡对发展的目的,研究者提出采用介质阻挡放电(DBD)等离子体技术对壁面附近的流场进行控制。作为一种典型的大气压放电等离子体技术,DBD等离子体激励仅需对局部流场输入能量或动量,即可影响局部或全局速度场及能量场[4],它在抑制流动分离[5]、减少汽封漏汽[6]、辅助燃烧调节[7]及翼型表面除霜[8]等领域均显示出优良效果,因此在壁面气膜冷却性能的提升方面具有良好的应用前景。De Giorgi等针对不同激励电压条件下,DBD微型激励器对亚声速压气机叶型吸力面流动分离的影响开展了数值研究,结果表明DBD等离子体激励可有效抑制叶片吸力面的流动分离,且压气机总压损失随激励电压的增大而减小[9]。Li等研究了DBD等离子体激励器沿展向布置时平板壁面的气膜冷却性能,结果表明,DBD等离子体激励对下游较远壁面处展向气膜冷却效率的提升程度较低[10]。Roth等提出了将DBD等离子体激励器沿流向布置的方案,该方案可诱导近壁面流场形成流向涡,因此又将其称为DBD-涡发生器(DBD-VG)[11]。Jukes等研究了DBD-VG等离子体激励诱导形成流向涡的机理,发现DBD-VG等离子体激励诱导的展向贴壁射流,是阻碍主流运动并使其抬升、翻卷及扭转形成流向涡的关键[12]。Shan等采用数值方法研究了组合型DBD-VGs等离子体激励器对流动分离的抑制作用,发现其可在壁面两侧诱导形成两簇反旋涡对,有效地克服湍流边界层内较大的逆压力梯度[13]。
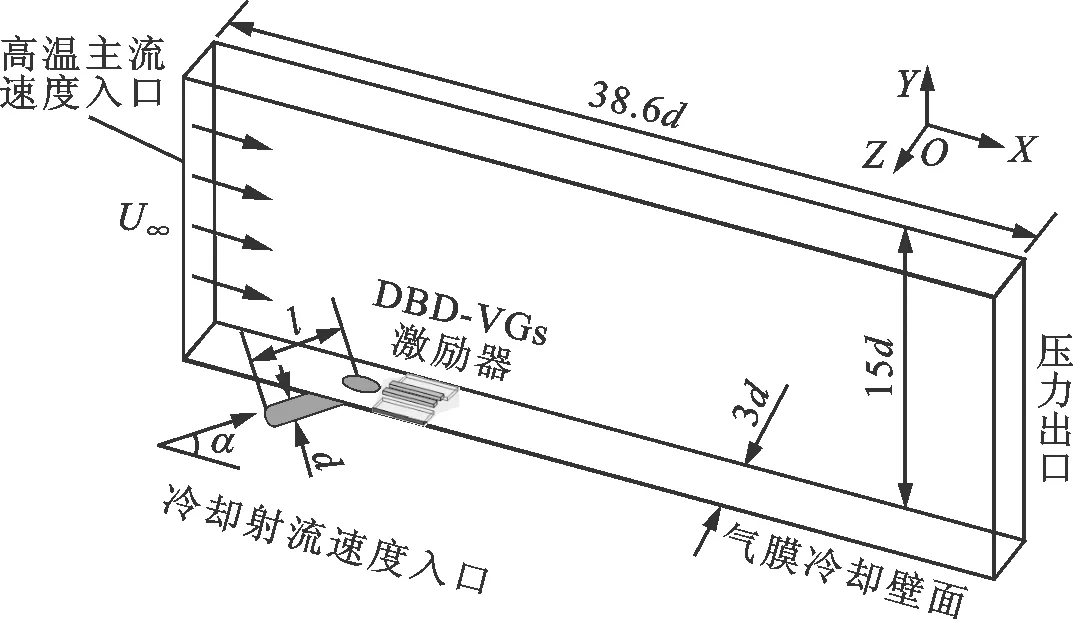
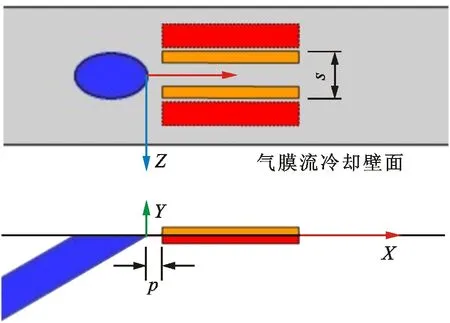
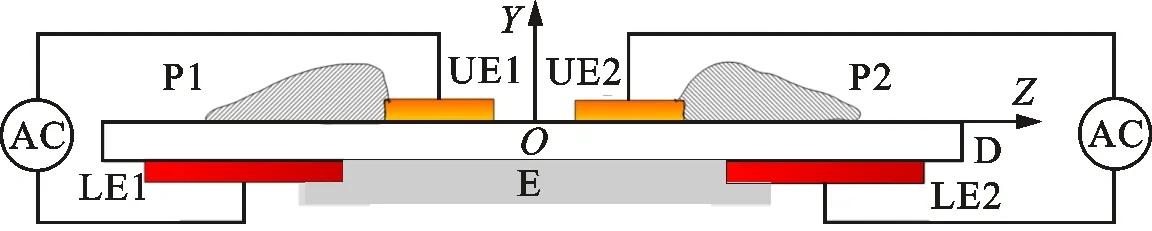
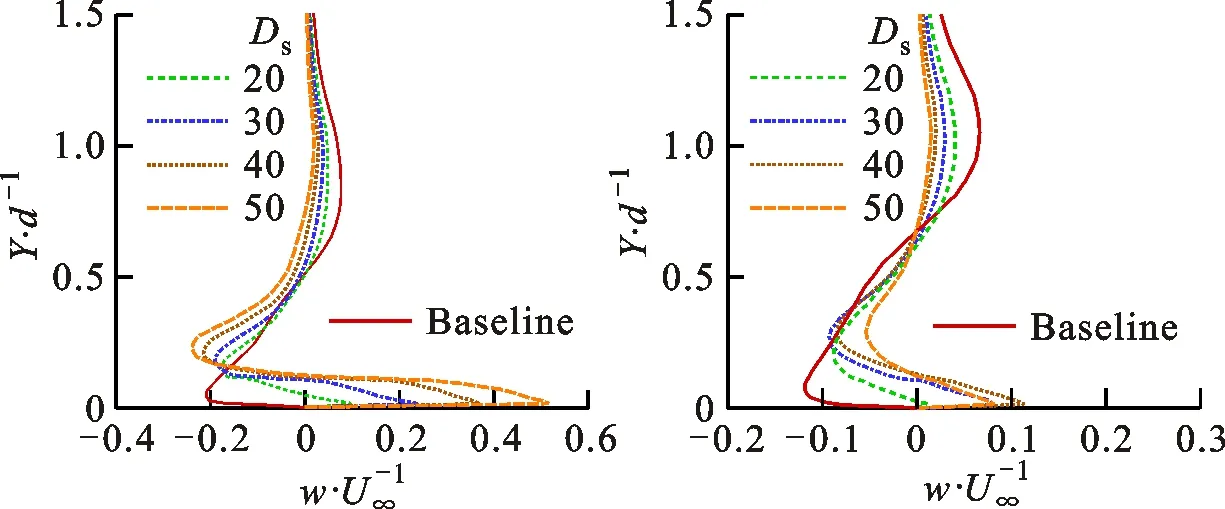
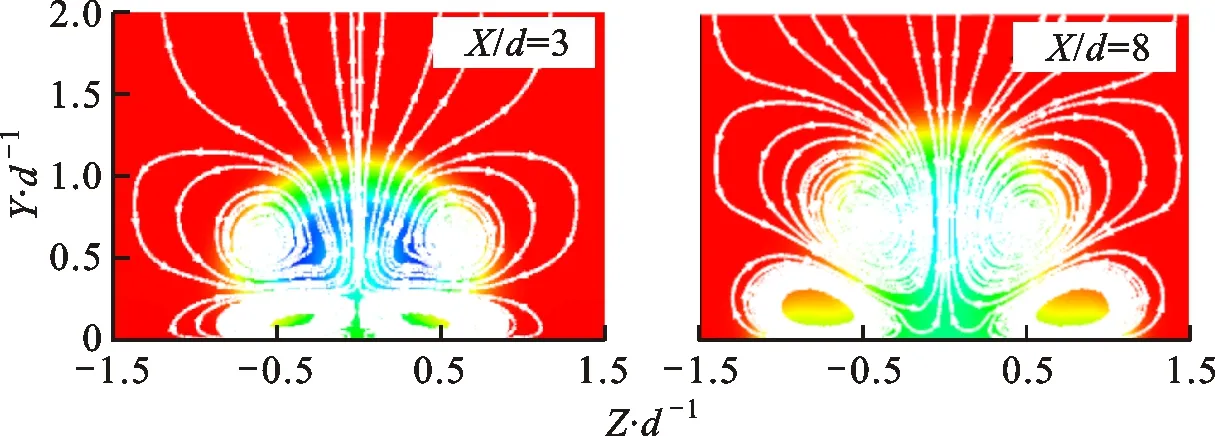
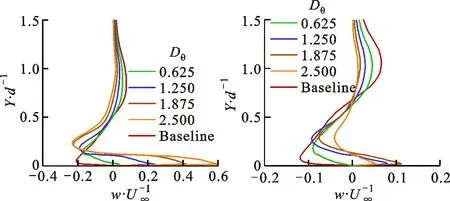
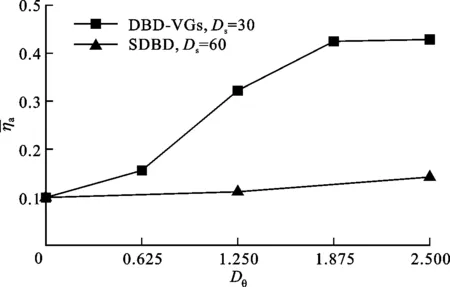
在DBD等离子体激励数值求解模型的研究方面,代表性的成果有Shyy等提出的基于电场线性化的等离子体激励模型[14],以及Matzgeller等建立的基于静电场方程组的电动激励力模型[15]。虽然二者求解思路不同,后者复杂度高于前者,但用于模拟平板准静态流场边界层内诱导的速度分布时,流向速度的计算曲线在0 mm 从公开发表的文献来看,尽管研究者针对DBD-VGs等离子体激励下近壁面区域的流动机理开展了实验及数值研究,但关于DBD-VGs等离子体激励参数对平板气膜冷却总体特性及流场结构影响的研究仍不系统。本文利用线性平均定常有效激励模型[14],将DBD-VGs等离子体激励力与RANS方程组相耦合,选取Realizablek-ε湍流模型对DBD-VGs等离子体激励条件下的壁面气膜冷却性能进行数值求解,并利用公开发表的实验和计算数据考核数值计算模型的有效性。在此基础上,分析DBD-VGs等离子体激励参数(归一化激励强度及归一化激励频率)对壁面气膜冷却性能的影响机制。 图1展示了DBD-VGs等离子体激励条件下的壁面气膜冷却性能求解模型。其中:冷却射流角α、冷却孔径d与冷却孔中轴线长度l分别为35°、12.5 mm及5.2d;主流进口平均速度U∞、总温T∞及边界层厚度δ分别为20 m·s-1、298 K及12.5 mm;冷气进口总温Tc=188 K;出口气流静压po=101.325 kPa;所有壁面均为绝热边界;两展向端面为周期性边界。 图1 计算域和边界示意图 DBD-VGs等离子体激励器在气膜冷却壁面上的位置如图2所示。其中,归一化流向距离p/d与归一化展向间距s/d分别为0.2及0.32。 图2 平板壁面上DBD-VGs激励器的位置 密度比RD及吹风比M的表达式分别为 RD=ρc/ρ∞ (1) M=ρcUc/ρ∞U∞ (2) 式中:ρc为冷却孔进口气流密度;ρ∞为来流进口气流密度;Uc为冷却孔进口气流平均速度;U∞为来流进口气流平均速度。本文假设所有气流均为理想气体,因此保持RD≈1.6。 归一化温度T*与绝热壁面冷却效率η的表达式分别为 T*=(T-Tc)/(T∞-Tc) (3) η=(T∞-Tw)/(T∞-Tc) (4) 式中:T为当地静温;Tc为冷却孔进口气流总温;T∞为来流进口气流总温;Tw为绝热壁面当地静温。 流向涡量ζx的表达式为 ζx=∂w/∂Y-∂v/∂Z (5) 式中:v为法向气流速度;w为展向气流速度。 归一化激励强度Ds及归一化激励频率Dθ的表达式分别为 Ds=(10ρceE0d)/(ρ∞U∞2) (6) Dθ=fd/U∞ (7) 式中:ρc为等离子体区域内的电子密度;e为电子的电荷量;E0为激励电场的源场强值[14];f表示外接交变电压的频率。 DBD-VGs等离子体激励装置的结构组成如图3a所示。在交变电源激励产生的非线性电场内,电场线及电场强度具有如下分布特征:暴露电极与覆盖电极的展向间距处电场线集中、场强较大,覆盖电极正对的介质表面处电场线分散、场强较小[14]。 因此,可将该非均匀电场线性化得到DBD-VGs等离子体激励的近似模型,如图3b所示。该模型的关键参数分别为:极板展向间隔L=0.5 mm;极板流向长度为3d;激励区域法向范围a=3 mm;激励区域展向范围b=6 mm。基于上述参数可获得线性定常平均电动激励力的分布函数,通过Fluent UDF将该激励力作为RANS方程组的源项,即可对DBD-VGs等离子体控制的壁面冷却性能进行求解。 (a)DBD-VGs等离子体激励器 (b)基于电场线性化的近似模型UE1、UE2—暴露电极;LE1、LE2—覆盖电极;D—绝缘的单层介质;E—环氧树脂;AC—外接交流电源;P1、P2—等离子体,仅在交变电压的半周期内形成[14]。图3 DBD-VGs激励及线性化近似示意图 计算域的网格模型如图4所示。为了保证y+<1,第一层近壁面网格的高度取为0.001 mm。冷却孔出口所在展向及流向壁面的网格密集程度均需提高。 图4 计算域的网格模型 图5展示了吹风比为0.5时网格无关性的考核数据。由图可见:网格数由400万增加到780万时,计算得到的壁面气膜冷却性能基本不变。据此,本文选用网格数为400万的网格,计算存在DBD-VGs等离子体激励时的壁面气膜冷却性能。 (a)壁面中线的冷却效率 (b)展向平均的冷却效率图5 网格无关性考核结果 利用Realizablek-ε湍流模型求解湍流方程,选用SIMPLE算法进行压力-速度关系计算,选择二阶格式进行空间离散。图6展示了吹风比为1时,壁面中线的气膜冷却效率ηc的计算值与实验值对比。由图可知:ηc的计算值与Sinha等[17]及Schmidt等[18]的实验值吻合良好,验证了本文数值方法的合理性。 图7展示了存在等离子体激励条件下,采用线性化的电动激励模型计算得到的近壁面归一化速度与文献值[14]的对比。从图中可看出,二者速度分布偏差较小,所以本文采用的线性定常平均电动激励模型的有效性得到了验证。 图6 壁面中线的冷却效率分布 图7 近壁面归一化速度分布 图8展示了吹风比为1、激励频率为1.25时,5种激励强度下Z/d=0.4平面上2个流向位置处的归一化展向速度分布。从图可见:与无DBD-VGs等离子体激励的工况对比,Ds≥20时近壁面展向速度曲线与w/U∞=0的曲线存在两个交点(不含壁面无滑移点),表明近壁面区存在两个位置相邻、旋向相反的涡旋。这是由于在DBD-VGs等离子体激励下,近壁面区域形成了与肾形涡对旋向相反的反肾形涡对。 (a)X/d=3(b)X/d=5图8 不同激励强度下各位置处的归一化速度曲线 (a)Z/d=0(b)Z/d=0.4 (c)Z/d=0.8(d)展向平均冷却效率图9 不同激励强度下壁面的冷却效率曲线 (a)俯视图 (b)主视图图10 不同激励强度下冷却孔附近的流线图 图10展示了吹风比为1、激励频率为1.25时,4种激励强度下冷却孔附近流线的主视及俯视图。由图可见:与无DBD-VGs等离子体激励的工况比较,当Ds提高时,孔口两侧高温主流被冷气向外缘(展向Z)排挤(见图10a标A和B处),下游冷、热气流掺混后的混合气流抬升程度减弱(见图10b标C和D处)。这表明DBD-VGs等离子体激励可有效抑制冷却孔下游附近的冷气抬升,使之贴近壁面流动,并能增强近壁面冷气沿展向的扩展性,可将原本与壁面接触的高温气流排挤至展向外侧区域,进而使得冷气与高温主流掺混边界高度降低,冷却孔下游壁面与冷气的展向接触范围拓展。 图11 不同激励强度下的壁面冷却效率云图 图11展示了吹风比为1、激励频率为1.25时,4种激励强度条件下的平板冷却效率云图。由图可见:与无DBD-VGs等离子体激励的工况对比可知,当Ds提高时,壁面冷却效率云图沿展向(Z方向)的扩张角增大,壁面附近冷气的展向覆盖范围扩展,平板气膜冷却性能的提升效果显著。这是因为部分冷气被DBD-VGs法向激励力沿负法向卷携,且DBD-VGs展向激励力可增加壁面附近的展向速度梯度,使得下游冷气与壁面的展向接触及流向扩展范围比无DBD-VGs等离子体激励时更大。因此,与无DBD-VGs等离子体激励工况对比,Ds≥20时下游壁面中线及展向平均气膜冷却效率的提高十分显著。例如Ds=30时,冷气在壁面X/d=8处的覆盖区域扩展了4倍。与DBD等离子体激励器沿展向布置时相比[10],DBD-VGs等离子体激励对下游较远(X/d>10)处近壁面冷气的展向覆盖范围具有更佳的扩展效果。 (a)无激励 (b)Ds=20 (c)Ds=30 (d)Ds=40图12 不同激励强度下各横截面的流线和温度云图 图12展示了吹风比为1、激励频率为1.25时,4种激励强度条件下横截面X/d=3,8内的T*和二维流线图。由图可见:与无DBD-VGs等离子体激励的工况比较,当Ds提高时,肾形涡对的尺度缩减、中心高度下降,反肾形涡对的尺度增大、中心高度上升。这表明DBD-VGs等离子体激励诱导形成的反肾形涡对涡旋强度增大,其对肾形涡对发展的抑制效果增强,肾形涡对使冷气抬升的作用减弱。因此,冷气与平板壁面的展向接触范围拓展,壁面气膜冷却性能得到显著改善。 图13展示了吹风比为1、激励强度为30时,中轴面内2个流向坐标处、5种激励频率下的近壁面展向速度w/U∞分布。由图可见:与无DBD-VGs等离子体激励的工况比较可得,Dθ≥1.25时归一化展向速度曲线与w/U∞=0的曲线均存在两个交点(不含壁面无滑移点),表明存在DBD-VGs等离子体激励时,壁面附近出现相邻但旋向相反的一对涡旋。这是因为DBD-VGs等离子体激励具有诱导近壁面区域产生反肾形涡对的能力,所形成的反肾形涡对的旋向与肾形涡对旋向相反。 (a)X/d=3(b)X/d=5图13 不同激励频率下中轴面内各处的近壁面速度曲线 (a)Z/d=0(b)Z/d=0.4 (c)Z/d=0.8(d)展向平均冷却效率图14 不同激励频率下平板壁面的冷却效率曲线 图15展示了吹风比为1、激励强度为30时,4种激励频率下中轴面内的归一化温度云图。由图可见:当Dθ提高时,壁面附近存在冷气流的法向区域减小,冷却孔出口冷气向壁面偏斜与沿流向扩展的程度均提高。与无DBD-VGs等离子体激励的工况比较,当Dθ=1.875时,X/d=11处的冷、热气流掺混边界下降至原高度的68.6%,说明DBD-VGs等离子体激励可有效抑制肾形涡对结构发展,减弱其抬升壁面附近冷气的作用,增强冷却孔下游冷气沿流向的延伸性,因此有利于提高冷气与壁面的接触程度,且可显著提升壁面冷却性能。 图15 不同激励频率下中轴面Z/d=0内的温度分布 图16 不同激励频率下平板的面积平均冷却效率 图17展示了吹风比为1、激励强度为30时,4种激励频率条件下2个横截面内流向涡量ζx的分布图。由图可见:当Dθ提高时,肾形涡对主体部分的中心下降且尺度减小,但是反肾形涡对的中心高度、涡旋尺度及强度均增大,并且近壁面涡量的展向延伸尺度显著提升。与无DBD-VGs等离子体激励的工况对比可得,Dθ=1.875时各截面内肾形涡对的中心降低、尺度减小,且反肾形涡对的涡旋强度及尺度最大。这说明DBD-VGs等离子体激励可诱导近壁面区域流体形成反肾形涡对,进而对肾形涡对结构发展起到间接抑制作用,并减弱其抬升壁面附近冷气的效果,从而使平板壁面的冷却特性得到显著改善。 (a)无激励 (b)Dθ=0.625 (c)Dθ=1.25 (d)Dθ=1.875图17 不同激励频率下各横截面内流向涡量的分布 综上可知,增大DBD-VGs等离子体激励参数时,平板气膜冷却的总体性能比无DBD-VGs等离子体激励的工况显著提升,冷却孔下游壁面附近流动结构得到明显改善,但实际应用等离子体流动控制技术时,须从收益和代价两方面权衡该技术的经济性。其中,可能的代价主要有:①激励器功率损耗[9,19]。外接交变电源的供电功率随DBD-VGs等离子体激励参数的提升而增大,但激励器的功率耗散导致用于激励等离子体的功率必小于总供电功率,因此在较大激励参数下,电功率损耗所致的附加成本可能超过冷却性能改善的收益,进而折损技术经济性。②激励器引起的流动损失。相较于无DBD-VGs等离子体激励的工况,直接暴露于来流气流中的上侧极板增加了壁面附近的流动阻力;另一方面,由于DBD-VGs等离子体激励诱导产生反肾形涡对与原有肾形涡对作用形成了复杂涡系结构,使得存在DBD-VGs等离子体激励时的整体流动损失与无激励时的大小关系具有不确定性。因此,进一步研究工作应围绕DBD-VGs等离子体激励器的功率损耗和壁面附近的流动损失等可能的代价展开,结合预期收益综合评价该方案的技术经济性。 本文在不同归一化激励强度和归一化激励频率条件下,对DBD-VGs等离子体激励影响壁面冷却性能及流场结构的机制进行数值研究,获得的主要结论如下。 (1)当激励强度提高时,冷却孔下游平板壁面气膜冷却效率的提升效果显著。激励强度为30时,壁面中线及展向平均的气膜冷却效率极值比无DBD-VGs等离子体激励的工况分别增大50%和286%。当激励强度提高时,冷气与壁面展向与流向接触范围均增大,冷、热气流的掺混边界沿壁面负法向移动,肾形涡对的尺度缩减、中心下沉,反肾形涡对的涡旋尺度及强度、涡旋中心高度、流向与展向扩展性均有所增大。在本文研究的工况范围下,激励强度不低于40时壁面冷却性能达到较佳效果。 (2)当激励频率提高时,冷却孔下游平板壁面冷却效率的提升效果明显改善。当激励频率为1.875时,壁面中线及展向平均的气膜冷却效率极值比无DBD-VGs等离子体激励的工况分别增大62.5%和460%。当激励频率提高时,壁面附近流体运动变化趋势与改变激励强度时类似。在本文研究的工况范围下,激励频率不低于1.875时平板气膜冷却具有较佳效果。 (3)与SDBD等离子体激励的工况对比可知,在较低激励参数下,DBD-VGs等离子体激励可使壁面面积平均冷却效率的提升效果更为显著;在相同激励参数条件下,DBD-VGs等离子体激励可使壁面附近冷气的展向覆盖范围更大。1 数值方法
1.1 计算模型
1.2 DBD-VGs激励模型

2 数值方法验证
2.1 网格无关性考核


2.2 计算方法验证


3 结果与讨论
3.1 激励强度对壁面冷却性能及流场结构的影响









3.2 激励频率对壁面冷却性能及流场结构的影响




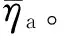




4 结 论
