基于自适应学习的5G通信系统信道估计方法
2022-08-10王昊
王昊
(中国信息通信研究院,北京 100191)
0 引言
信号估计通常采用导频、半盲估计、盲估计来实现[1-4]。盲道估计需要获取大量的信号信息,计算复杂度高、实时性差,不能满足5G 用户低时延的需求。半盲估计通过少量导频获得信道参数的初始值,采用信号反馈的方式结合后验信息进行完整信道参数的似然估计。基于导频的信道估计方法是在信号发送过程中插入不承载有用信息且收发双方已知的训练序列或者导频符号,接收端根据导频信号实现信道估计[5-6]。与半盲估计、盲估计相比,基于导频的信号估计方法具有复杂度低、方法简单等优点,因此受到广泛应用。
基于导频的信道估计性能受到导频设计和估计算法的影响,因此不少学者针对上述两方面做了大量的研究。Hassibi 等人[7]指出,在不相关的瑞丽衰落信道中,最优导频信号应该是正交的,而且导频的长度应该等于天线的数量,该方法很难适用于5G 的大规模多输入多输出(MIMO)系统;Duly 等人[8]借助信道反馈来实现导频信号的调优,以期降低接收端产生的符号间干扰、码间串扰等影响,进而提升信道估计精度;Wang 等人[9]则利用信道时间和空间的相关性,采用相关算法来最小化信道估计的均方误差,进而优化导频序列;You 等人[10]采用信道二阶统计的方法来分配导频,保障使用相同导频的用户对应相互正交的信道矩阵,从而避免信道污染的问题;Li 等人[11]基于信道时间相关性,提出深度神经网络的信道状态信息反馈方案,有效降低信道状态信息反馈开销和提升信道状态信息反馈精度;He 等人[12]采用压缩感知的稀疏信道估计来获得更好的信道估计结果,该方法能较好对抗导频干扰;Qi 等人[13]提出一种基于稀疏转换方法的信道估计方法,该方法能够实现有限导频开销条件下的多信道参数估计。
上述的导频设计和估计算法都是基于小规模MIMOOFDM 或者SISO-OFDM 信道系统设计的,未考虑大规模多天线系统中环境的动态变化、系统开销和计算复杂度的影响,因此无法直接扩展到大规模MIMO 系统中。针对该问题,本文提出一种基于BP 神经网络的5G 通信系统信道估计方法,为了降低信道估计的系统开销和计算复杂度,将信道估计模型定义为回归拟合;为了应对环境动态变化和实际场景与训练数据不一致的问题,采用在线训练小样本数据的方式,融合集成学习的方法迭代优化模型,以实现模型的高适用性。
1 基于神经网络的信道估计初始模型构建
受到多径效应的影响,无线信道估计呈现较强的非线性特征。采用何种方法快速学习信道传输参数的非线性映射,并且各信道传输参数具有良好的适应性是信道估计的关键问题。本文采用深度学习的方法,通过对大量数据的离线学习,迭代训练得到信道参数的自回归系数,以实现传输参数的非线性映射,获得初步的信道估计模型。
1.1 系统模型
假设大规模MIMO-OFDM 系统中,发射天线个数为Nt,接收天线个数为Nr。则第n个发射天线的一个OFDM 符号表示为:



其中,yk、xk、wk、Hk分别表示为:
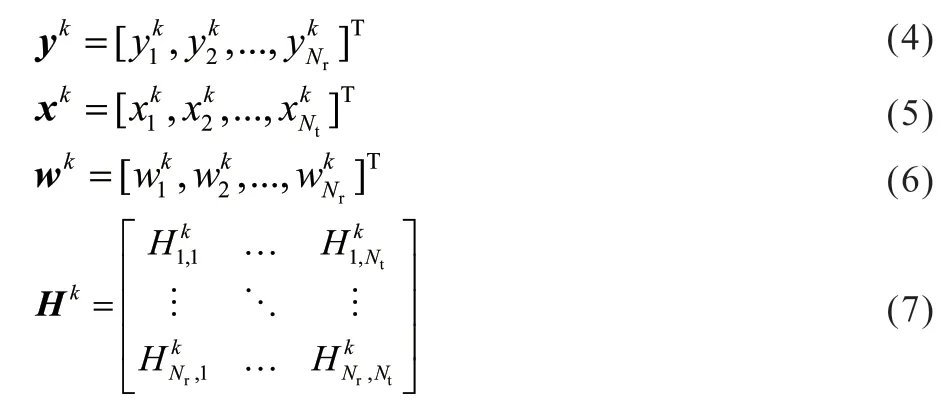
1.2 基于神经网络的信道估计初始模型
为了对Hk进行有效估计,必须设置合理的信道估计算法。考虑到发送天线和接收天线以及子载波数量较大的情况下,采用线性估计的算法所得到的准确率很难达到实际应用的标准,因此本文采用大数据的方法,利用神经网络的方法对大量离线数据进行训练,学习无线信道的状态特征,尽可能获取传输信道的频域变化特征。那么,为了学习所有子载波的信道状态,采用BP 神经网络对大量离线数据进行信道估计,定义损失函数为:

其中,Hi为子载波i的实际信道状态,为神经网络输出的子载波i的信道状态矩阵。为了得出HDNN,本文将发射信道x和接收信号y作为神经网络的输入,以已知的信道实际状态信息H作为标签对神经网络进行有监督的训练,最终得出神经网络优化有的信道状态矩阵HDNN作为神经网络的输出。神经网络的离线训练过程如图1 所示:

图1 神经网络离线训练过程
2 基于在线集成学习的信道估计自适应优化模型
从大量离线数据对信道状态矩阵进行训练从而构建信道估计初始模型,直接使用很难适用于动态的信道时域变化环境。除此之外,信道估计模型与用户使用业务量有一定的关系,不同时间(忙闲时)尺度下,信道估计受到的外部干扰也是不同的,因此基于离线大数据下的信道估计初始模型不能用于不同区域、不同时间段的信道估计,否则,其预测准确性和性能将会大打折扣。为此,本文通过在线集成学习的方法对初始的信道估计模型进行优化。由于发送和接收的数据是持续更新的,通过对新一批数据进行训练,生成一个新的信道估计模型,并对比信道估计初始模型的性能,对初始信道估计模型进行权重更新;基于更新后的权重,采用加权平均的方法调整每一个信道估计模型的权重,形成一个在线优化的信道估计模型,实现信道估计参数的自适应学习。基于在线集成学习的信道估计优化模型过程如图2 所示。
3 仿真实验与结果分析
3.1 实验说明
为了对本文模型进行验证,通过将LS 信道估计和BLMMSE 信道估计两种经典的信道估计方法与本文模型进行对比,将比较不同信噪比、不同长度的导频下两种场景下的信道估计精度。LS 信道估计通过最小二乘法来实现信道的估计。BLMMSE 信道估计是将信号分解成线性变量,然后再通过最小二乘法实现信道估计。由此看出,BLMMSE 信道估计能够较好应对非线性映射的问题,具有较高的估计精度。
仿真使用相关的信道参数如表1 所示。

表1 仿真实验中的相关信道参数
3.2 实验结果分析
(1)不同信噪比下三种估计方法的估计精度对比
从图3 可知,主坐标轴对应LS 信道估计和BLMMSE 信道估计误差;次坐标轴对应本文信道估计误差。本文信道估计模型在不同信道比下的性能都是最优的;LS 信道估计和BLMMSE 信道估计方法不仅对信噪的变化十分敏感,而且在低信噪比时的估计精度不高。这是因为在低信噪比的状态下,不同的信道所对应的标签值差异性很小,在这种标签差异性很小的情况下,LS信道估计和BLMMSE 信道估计方法很难建立起精确的映射关系。而本文模型采用在线数据不断优化模型,通过迭代的方式构建起精确的映射关系,实现信噪比波动场景下信道估计参数的自适应学习。
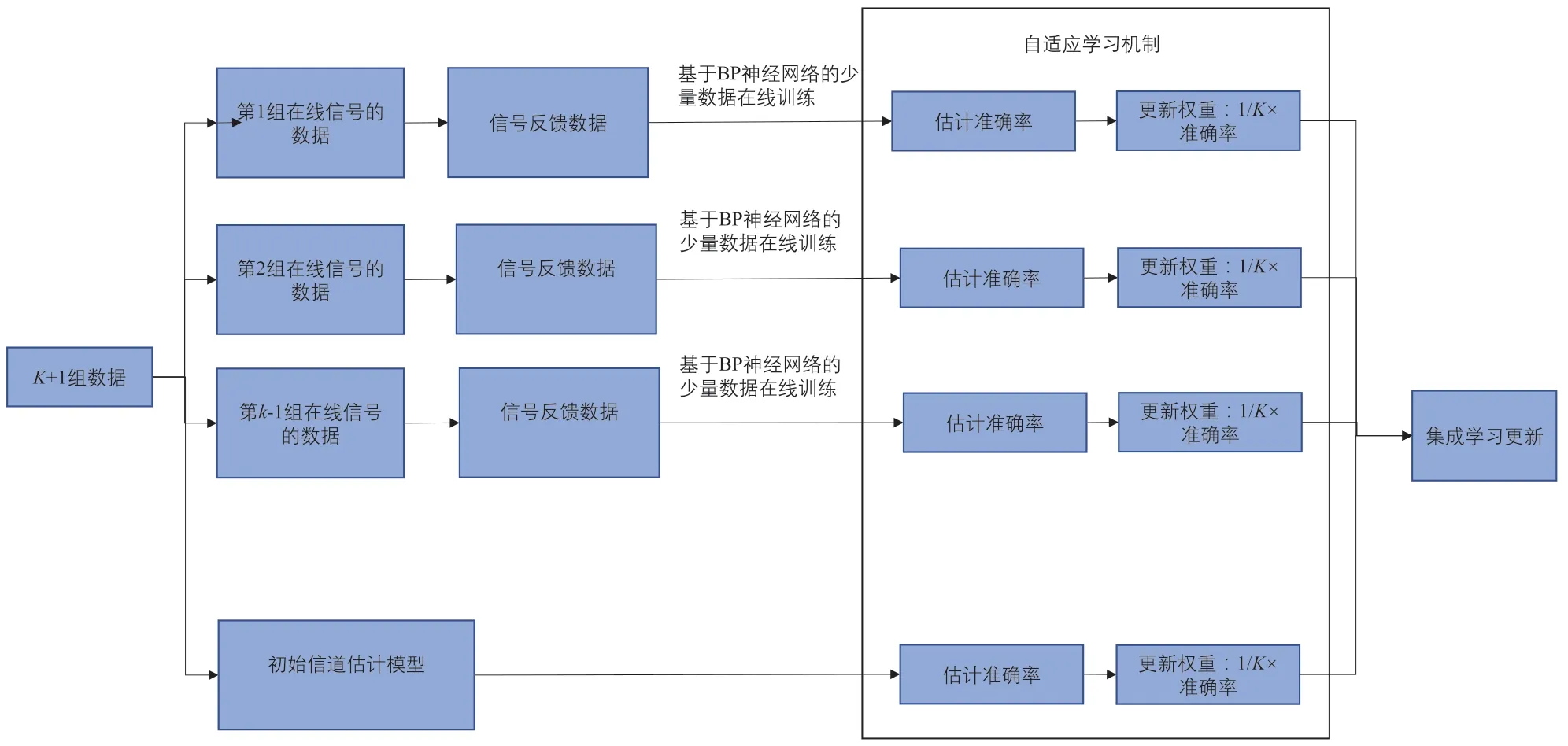
图2 基于在线集成学习的信道估计优化模型

图3 不同信噪比下三种估计方法的估计精度对比
(2)不同长度导频下三种估计方法的估计精度对比
从图4 可知,主坐标轴对应LS 信道估计和BLMMSE 信道估计误差;次坐标轴对应本文信道估计误差。本文信道估计模型在不同导频长度下的性能都是最优的,LS 信道估计和BLMMSE 信道估计方法不仅对导频长度的变化相对敏感,而且在导频长度时,由于天线数量较高(天线数量是100),其信道的估计精度较低。本文将每5 个采样间隙划分成一个数据块,每个采样间隙下的第一个数据块被设计为导频时,其他4 个信道数据通过第一个数据块来估计,在天线数越多、低长度导频的情况下,越小的导频长度的差异性很小,在这种标签差异性很小的情况下,LS 信道估计和BLMMSE 信道估计方法很难建立起精确的映射关系。而本文模型采用在线数据不断优化模型,通过迭代的方式构建起精确的映射关系,较好地应对导频长度变化的情况。

图4 不同导频长度下三种估计方法的估计精度对比
4 结束语
本文提出一种基于自适应学习的5G 通信系统信道估计方法,该方法将信道估计问题分解为回归拟合和在线自适应集成优化两个子问题。采用BP 神经网络对大量离线数据进行训练,充分学习无线信道的状态特征,获取无线信道的初始模型;并在此基础上,采用在线数据迭代更新模型的方式,融合集成学习实现信道估计参数的自适应优化;最后,本文设计仿真实验,从不同信噪比和不同导频长度下证明了本文算法的鲁棒性和有效性。综上所述,本文提出的信道估计方法具有扩展性和实用性。
