分段CRC 辅助极化码SCL 比特翻转译码算法

崔建明，王庆祥，张小军，李恒忠

（山东科技大学，山东 青岛 266590）

0 引 言

极化码是一种可以严格证明达到香农极限[1]的编码方案，是5G 信道编码技术之一。文献[1]提出串行抵消（Successive Cancellation，SC）译码算法，但是SC 译码器在有限码长下，其译码算法纠错性能不理想。为获得更好的译码效果，极化码串行抵消列表（Successive Cancellation List，SCL）译码器[2]，始终保持L条最佳候选路径，可实现接近最大似然（ML）译码的性能，但其列表较大，计算复杂度较高。CRC 辅助SCL（CRC-Aided SCL，CA-SCL）译码算法[3]通过在信息比特序列后添加CRC 检验，筛选出最优的候选路径，以此提高译码性能。在此基础上，又提出一种分段CRC 辅助SCL 译码方案[4]，该方案可显著降低译码复杂度。类似地，CRC 纠错辅助连续抵消列表（CRC-EC-SCL）译码的基本译码方案[5]也从另一角度提高译码性能。与CRC-polar codes类似的还有Hash-polar codes[6]，其检验位可以分散在信息位里，性能优于奇偶检验极化码。

在SC 译码过程中，信道噪声或由于先前错误比特引起的错误传播是产生错误比特的原因，通过对引起错误传播的第一个错误比特翻转，可获得较好的性能增益。根据译码树结构，总结出极化码三种相应的节点类型[7]，提供节点合并，以减少译码器延迟。基于翻转译码的思想，一种翻转译码算法[8]被提出，通过对数似然比（Log Likelihood Ratio，LLR）的绝对值大小来确定阈值，作为翻转译码的依据。由于信道中可能存在多比特错误，在翻转1 比特错误码字的基础上，提出一种改进的翻转多比特的SC 译码器[9]，以此提高译码性能。为进一步降低译码复杂度，分段SC 比特翻转译码算法[10]被提出。为在翻转过程中更高效地确定关键集合，文献[11]中阐述了用树结构确定关键集合的方法。基于该构造关键集合的方法，同样将比特翻转用到SCL 译码算法中，进而提出一种改进关键集合的方法[12]，并根据该构造方法，提出了串行抵消列表比特翻转（Successive Cancellation List Bit-Flip，SCLF）译码算法。

为降低SCLF 译码算法的译码延迟，基于提出的改进的关键集合[12]，本文提出一种分段CRC 辅助串行抵消列表比特翻转极化码译码（Low-Complexity Segmented CRC-Aided SCL Bit-Flip Decoding of Polar Codes，SCASCLF）算法。根据信息位置序列，该译码算法将译码过程分为前后两段，在译码失败情况下尝试比特翻转译码，并根据每段中的位置信息，采用SCLF 确定关键集的方法确定每段中的关键集合，在每段译码过程中，利用CRC 校验对译码结果进行判断，每段只保留一条正确的路径。另外，本文还提出了多比特翻转错误码字的方法，可使译码结果更准确。本文采用多比特翻转译码与分段CRC 辅助SCL 比特翻转译码相结合，大大降低了译码复杂度。

1 极化码

1.1 极化码编码和译码

极化码利用K个最可靠的比特信道发送信息比特，其他信道发送固定比特。码长为N的极化码，信息比特与固定比特混合编码得到发送码字序列uN1=(u1,u2,…,uN)，对应的固定比特集合和非固定比特集合分别用uAC和uA表示。经过信道传输后，在接收端得到接收码字序列yN1=(y1,y2,…,yN)，在译码器中完成码字估计uN1=(u1,u2,…,uN)，W(|y x)表示传递概率。如果ui是固定比特，则ui=0；否则，SC 译码器计算每个比特信道的对数似然比（LLR）：

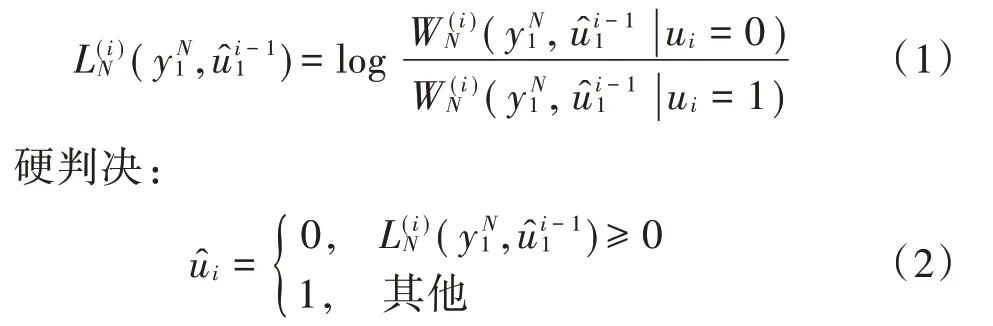
译码树中，白色的叶子节点代表固定比特节点，黑色的叶子节点代表信息比特节点。给定一个译码树节点V，令vp，vl和vr分别表示父节点、左孩子节点和右孩子节点，图1 中给出极化码（16，8）的SC 译码树，节点V的译码单元如实线框中所示。

图1 极化码（16，8）译码树

SCL 译码器是从所有路径中选取路径度量值最大的L条搜索路径作为候选路径，并添加CRC 校验比特来筛选候选路径。

1.2 关键集的构建

关键集（Critical Set，CS）选择最不可靠的信息比特进行构建，通过翻转CS 中信息比特提升译码性能。用该构建关键集合方法[11]，确定出最不可靠的叶子节点集（u7，u9，u10，u12）对应的索引序号作为翻转译码的关键集合。根据该方法依次对所有叶子节点进行筛选，构建比特翻转关键集合。根据确定的关键集合进行比特翻转译码。

2 提出的译码算法

本文通过采用多比特翻转译码和分段CRC 辅助SCL 比特翻转译码结合以提高译码性能。

2.1 CA-SCL 多比特翻转译码算法

根据信道噪声引起的不同错误比特概率的分析，表明1 位错和2 位错是影响极化码译码性能的主要原因。因此，本文采用翻转2 bit译码方案，如图2 所示。

图2 翻转2 bit CA-SCL（N，K +r）译码器流程图

2.2 SCA-SCLF 译码算法

本文中，CA-SCL（P=x）表示分x段CRC 辅助SCL译码算法，SCA-SCLF（P=x，ω）表示分x段CRC 辅助SCL 翻转ωbit 译码算法的情况。在分段极化码编码部分，将CRC 分配到每一段中进行极化码编码。首先依据各段的信息位置对关键集进行分段，各段的关键集合用T P1=(T1,T2,…,TP)表示，其对应的索引表示为ρP1=(ρ1,ρ2,…,ρP)。在译码中，根据接收到的传递结果yN1进行译码。分两段CRC 辅助SCL 翻转1 bit 的译码过程如算法1 所示。

根据各段先后顺序，依次进行译码（第2 行）。首先进行传统的CA-SCL 译码（第3～4 行），如果译码成功且不是最后一段，则保存译码结果，然后对后续的段进行译码（第18～19 行）。如果是最后一段，则译码正确，结束本帧译码（第20～21 行），反之，译码失败，执行翻转1 bit 译码过程。根据CS 中的信息比特索引，执行比特翻转，尝试译码（第7 行），如果通过CRC 校验且不是最后一段，则转到第2 行进行下一段译码，如果是最后一段，则终止译码过程（第8～12 行）。如果通过翻转CS中对应的信息比特后译码失败，程序提前终止，不再执行后续段译码（第15～17 行）。

算法1：SCA-SCLF（P=2，1）译码算法

极化码SCA-SCLF（P=2，2）译码过程如算法2 所示。应当注意，后一段译码是基于前一段中保留的候选路径，如果翻转1 bit 译码失败，CS 中的信息位置需要进行非重复索引的成对组合，执行翻转2 bit 译码。如果翻转2 bit 译码仍然失败，译码将提前终止，节省了译码等待时间。

算法2：SCA-SCLF（P=2，2）译码算法

另外，与原来的译码过程相比，分段CRC 辅助SCL翻转2 bit 译码算法，缩小了每段对应的关键集合规模，并减少了尝试执行翻转2 bit 的组合数量，整体的译码复杂度将大大降低。

3 性能仿真及译码复杂度分析

本文中采用加性高斯白噪声（Additive White Gaussian Noise，AWGN）信道和二进制相移键控（Binary Phase Shift Keying，BPSK）调制。12 位和24 位的CRC 生成多项式分别为：

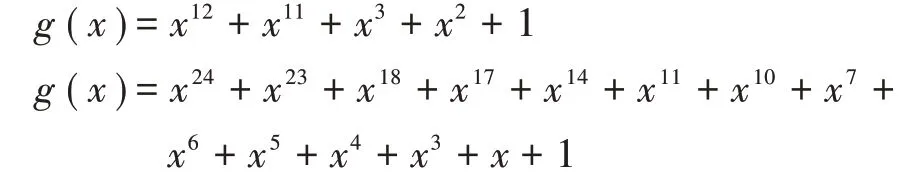
3.1 性能仿真

极化码（256，128+24）和（512，256+24）在L=8 和L=16 时的译码性能如图3 和图4 所示。在相同的CRC 条件下，翻转2 bit 比翻转1 bit 有更好的译码性能，分段翻转译码比不分段有更好的译码性能。图3 中，当L=8，误帧率（Frame Error Rate，FER）为10-1时，对于极化码（256，128+24），SCA-SCLF（P=2，2）比CA-SCL 获得0.3 dB 的性能增益；FER 为10-2时，对于极化码（512，256+24），SCA-SCLF（P=2，2）比CA-SCL 获得性能增益为0.2 dB。图4 中，L=16 下，在FER 为10-2时，对于极化码（256，128+24），SCLF-ω=2 比SCLF-ω=1 可获得0.1 dB的性能增益，SCA-SCLF（P=2，2）比CA-SCL 获得性能增益为0.3 dB。

3.2 译码复杂度分析

本文通过译码过程中更新的节点次数统计计算复杂度。令sum 代表数据量的大小，compl_SC 表示传统SC 算法的译码复杂度，compl_ave 表示平均计算复杂度，即更新的平均节点次数：

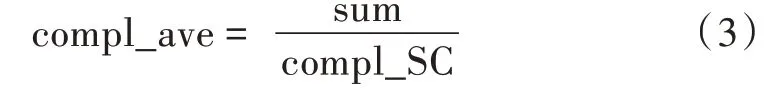
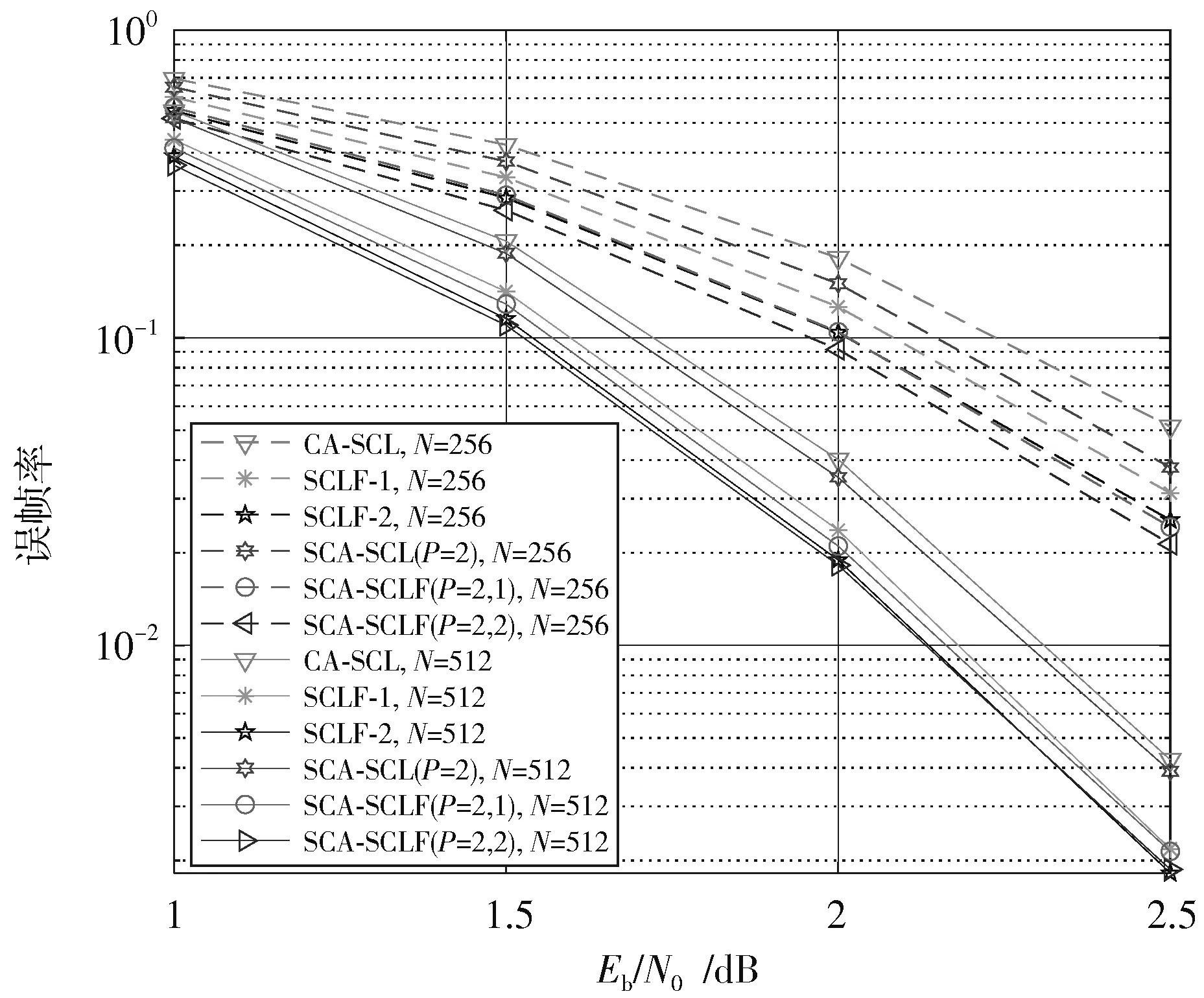
图3 极化码（256，128+24）和（512，256+24）L=8 的误帧率

图4 极化码（256，128+24）和（512，256+24）L=16 的误帧率

根据式（3）得到图5 和图6 的复杂度对比。图5 中，L=8 时，在EbN0为1.5 dB 下，极化码（256，128+24）SCASCLF（P=2，1）比SCLF-ω=1 译码复杂度可降低47.7%，SCA-SCLF（P=2，2）算法比SCLF-ω=2 译码复杂度可降低69.9%；同样，极化码（512，256+24）SCA-SCLF（P=2，1）算法比SCLF-ω=1 译码复杂度可降低46.3%，SCA-SCLF（P=2，2）比SCLF-ω=2 译码复杂度可降低71.9%；图6中，L=16 下，在EbN0为1.5 dB 下，极化码（256，128+24）SCA-SCLF（P=2，1）比SCLF-ω=1 译码复杂度可降低48.6%；在EbN0为2 dB 下，极化码（512，256+24）SCASCLF（P=2，2）比SCLF-ω=2 译码复杂度可降低62.5%；在EbN0为1 dB 下，SCA-SCLF（P=2，1）算法比SCLF-ω=1译码复杂度可降低47.6%，在EbN0为1.5 dB 下，SCASCLF（P=2，2）算法比SCLF-ω=2 译码复杂度可降低58.8%。

图5 极化码（256，128+24）和（512，256+24）L=8 的平均译码复杂度对比

在相同的CRC 条件下，分段翻转1 bit 译码比不分段翻转1 bit 时复杂度更低；在相同的条件下，分段翻转2 bit 译码比不分段翻转2 bit 时复杂度更低。基于分段译码，首先对前一段进行CRC 校验，如果校验失败就会终止译码，反之继续进行下一段译码过程，通过该过程可抑制错误传播，降低译码复杂度，其降低的程度与CRC 校验能力和发生错误的个数有关。高EbN0下，错误比特较少，降低复杂度的程度不明显；低EbN0下，存在更多的错误比特且比特翻转校正能力受到限制。由于原来SCLF 译码算法中只能进行纠正1 bit 错误码字，使用SCLF 译码算法翻转2 bit 会造成较高的译码延迟，而采用SCA-SCLF 译码算法可大大降低译码复杂度。

4 结 语

本文提出一种分段CRC 辅助SCL 比特翻转译码算法，该算法可纠正多比特错误，具有良好的译码性能；针对比特翻转引起的译码复杂度较高的问题，该算法可降低译码延迟。仿真结果表明，采用分两段翻转2 bit 译码算法比使用SCLF 方法进行翻转2 bit 译码算法具有更好的译码效果，当L=8，在EbN0=1.5 dB 时，极化码（512，256+24）SCA-SCLF（P=2，2）比SCLF-ω=2 译码算法复杂度降低71.9%。

注：本文通讯作者为张小军。