改进深度学习算法的对称翼型流场再现

杨从新,凌祖光,王岩,钱晨,赵斌,周楠楠

(1.兰州理工大学能源与动力工程学院,730050,兰州;2中国核动力研究设计院,610000,成都)

计算流体力学(CFD)方法广泛应用于流场的数值计算,朱志斌等采用大涡模拟(LES)方法计算低雷诺数翼型层流分离流动中涡系结构的时空演化过程、均化流场以及雷诺应力等脉动参数分布特征[1];时北极等利用滑移速度壁模型构建等效体积力,并采用浸入边界与壁模型相结合的大涡模拟方法对雷诺数为1.2×106的回转体绕流计算,验证大涡模拟方法在高雷诺数下的准确性[2]。上述学者的研究成果表明数值模拟方法能够获得很高的计算精度,但CFD方法通常需要消耗大量的计算资源与时间,而且难以重复利用数值计算结果。赵松原等提出借助降阶模型[3]提取流场主要特征构造函数以减少计算时间,但降阶模型对流场参数变化较为敏感,鲁棒性不佳[4]。近年来,深度学习方法依靠强大的特征学习能力,广泛应用于各个领域,这也为流场预测提供新思路。

目前已有部分学者将深度学习方法应用于流场预测中,如Miyanawala等利用卷积神经网络(CNN),成功预测了不同几何外形柱体的流体载荷[5];Lee等采用生成对抗网络来学习全阶Navier-Stokes方程的非定常数值解,通过对两个雷诺数下二维圆柱绕流全阶数值解的学习,就能够准确预测出介于两个雷诺数之间的二维圆柱尾流融合的非定常过程[6];何磊等通过对比克里金法、径向基神经网络方法及支持向量机方法,并应用于火箭气动特性建模[7];惠心雨等利用回归生成对抗网络学习圆柱绕流非定常流动,成功预测不同时刻圆柱绕流的流场参数,并将回归生成对抗网络、条件生成对抗网络和真实样本之间的误差进行对比[8]。上述学者的研究表明深度学习方法具有预测复杂流场的能力。

此外,针对特定问题,亦有学者选择改进激活函数以达到更高计算精度。例如,Maas等改进神经网络的激活函数为线性修正单元(Leaky ReLU),相比传统线性整流函数(ReLU)[9],Leaky ReLU在语音识别的噪声分离上能获得更好的结果[10];Klambauer等通过理论推导,将ELU激活函数改进为SELU激活函数[11],使神经网络具有更好的鲁棒性。

由上述研究可知,改进激活函数能获得更加精确的计算结果,但目前针对流场计算的激活函数较少。本文基于全连接神经网络,设计了一种能够通过迁移学习算法约束并预测一定攻角和雷诺数范围内NACA0018翼型流场的激活函数,使改进激活函数能根据所给出的雷诺数,预测小攻角下NACA0018翼型压力场、速度场。

1 深度神经网络

深度学习作为一种人工智能方法,通常由深度神经网络算法实现,根据学习方式不同可以分为监督式学习、半监督式学习与无监督式学习。相比半监督学习与无监督学习,监督学习是一种能快速建立输入标签与输出变量关系的机器学习方法[12],在有标签的情况下可以快速精准拟合映射关系,故本文采用监督式学习方法下的全连接神经网络预测NACA0018翼型的外流场。

1.1 全连接神经网络

全连接神经网络指神经网络每一个连接层的每个结点都与上一层的所有结点相连,通过全连接逐级完成特征提取[13],计算公式如下

(1)

式中:X是输入参数;b是偏置;Y为输出参数;W是权重系数。

全连接层的正向传播和反向传播均以矩阵计算完成,通过权重系数和偏置计算获得输入参数与输出结果的线性关系,最后通过激活函数的非线性变换获得输入与输出的非线性映射关系。其基本思想是每一次训练结束,通过链式求导法则反向传播误差,修正权重,直到训练结束。

1.2 神经网络方法流程

采用改进激活函数的全连接神经网络进行流场预测,训练的主要流程如图1所示,将CFD计算结果作为真实样本,并将其分为互斥的训练集和测试集。构建全连接神经网络,将训练集样本数据输入神经网络,调整超参数使之在训练集上具有较小的损失以获得准确预测的模型。保存训练完成的模型后将预测数据输入神经网络,得到压力场与速度场,并与真实样本对比,验证预测模型的准确性。

1.3 获取样本集

本次预测采用NACA0018翼型作为研究对象,该翼型具有升阻比大、后缘分离缓慢等优点[14-15],被广泛应用于垂直轴风力机中[16]。翼型弦长C=1 m,通过改变来流速度控制雷诺数的变化。利用ANSYS ICEM进行网格划分,计算模型如图2a所示,翼型前缘到进口边界、出口边界的距离分别为15C和20C,全局采用C型结构化网格。对翼型近壁面进行网格加密,如图2b,为保证壁面y+<1[17],边界层法向第一层网格高度设置为1.5×10-5m,网格增长率为1.05,总网格数为17万,满足SSTK-ω模型的计算要求。利用FLUENT软件进行数值计算,动量、湍动能和压力均采用二阶迎风格式离散,压力-速度耦合器采用SIMPLEC算法,边界条件设置为速度进口、压力出口,翼型表面设置为绝热无滑移壁面,计算攻角α=2°,4°,6°,8°,计算完成后对比升力系数与实验的误差如图3所示[18]。

(a)整体网格划分(b)局部放大图 图2 计算与训练网络

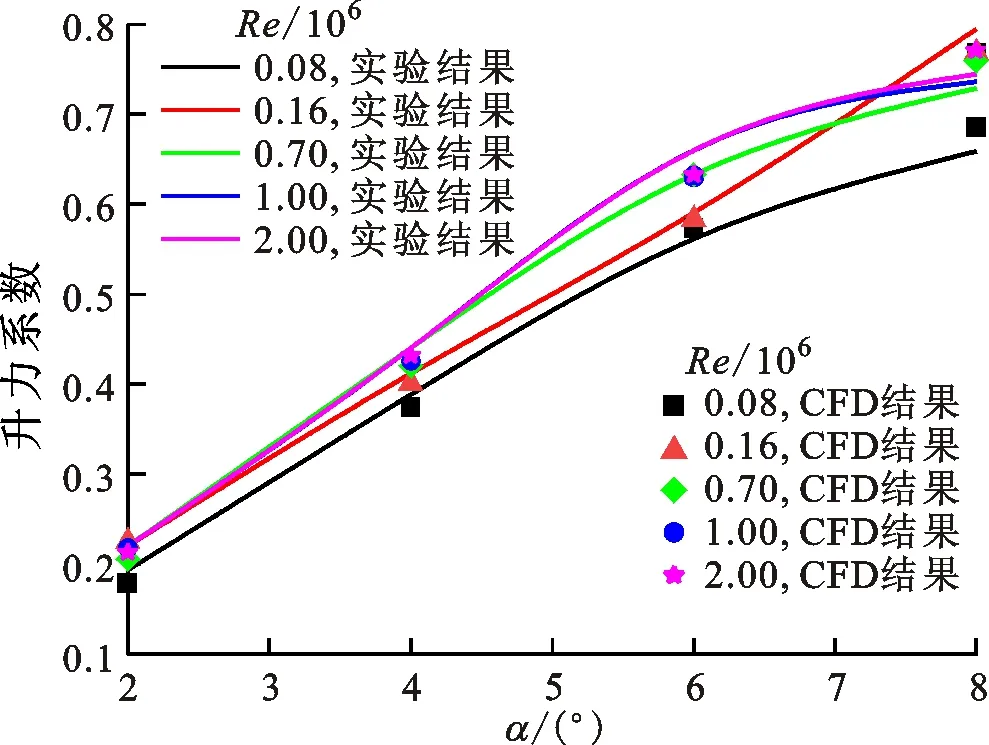
图3 升力系数的数值模拟与实验对比

由图3可以看出,CFD方法能够获得较高精度,其预测误差均小于5%。舍弃头尾雷诺数,最终利用CFD方法重新获得NACA0018翼型在α=2°,4°,6°,8°、Re=0.1×106～1.6×106下的压力场、速度场作为真实样本各140组数据,并将其随机分为132组训练集和8组测试集,来验证神经网络的准确性。

1.4 激活函数的设计

因为流场中同一点速度和压力满足守恒方程,存在相互约束的情况,因此利用流场中速度与压力的关系来构造激活函数,并行输出速度场与压力场,使输出结果相互约束,加速收敛。

速度场采用Leaky ReLU激活函数计算,激活函数如下

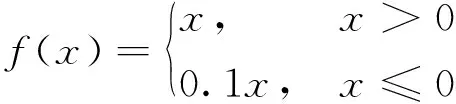
(2)

式中:x是输入自变量;f(x)是输出结果。

由于翼型的升阻力系数主要取决于翼型表面压力分布,综合压力场与速度场能量守恒关系,采用圆柱绕流流场速度公式近似推导动压与静压的关系,其速度分布[19]如下

(3)

式中:v∞是无穷远处来流速度;v是流场中任一点速度。在流场中的某一点可认为v∝v∞,根据能量守恒,简化后的伯努利方程如下

(4)

式中:p是流场中某一点压强;p∞是无穷远处来流压强;ρ是流体密度;g是重力加速度。

流场中任意一点速度与压力近似呈现二次关系[19]。考虑到速度压力激活函数适应性,设计激活函数如下

(5)

式中:x是输入自变量;f(x)是输出结果。

由于在计算过程中进行了简化近似,为修正简化过程对预测精度影响,在改进激活函数后添加使用传统SELU激活函数的网络层对预测数据进行修正。

1.5 损失函数与优化器选择

损失函数用于计算模型预测值与预期输出之间的相似程度,针对不同的问题,需要采用合理的的损失函数,将损失函数值降至最小是预测的最终目标。

由于流场预测的问题属于回归问题,本次预测采用平均绝对误差作为损失函数(MAE),以真实样本和预测样本的差值作为损失函数反向运算,表达式如下

(6)

优化器采用Adam方法[20],该方法适合多参数的计算,相比于动量梯度下降方法和RMS prop方法等具有计算效率高、内存要求少的优点。

1.6 训练模型

采用python语言和tensorflow2.0深度学习框架搭建神经网络及数据处理程序,其中神经网络输入参数为雷诺数,输出参数为翼型的压力场、速度场。

如图4所示:神经网络第1、2层用于拉伸数据维度,因此采用线性激活函数(Linear)以加快计算速度;在3～6层将数据进行非线性变换,映射到样本标记空间进行非线性的激活和学习;在隐藏层6之后采用迁移学习方法思想;隐藏层7与隐藏层7′将隐藏层6的输出参数分别使用自定义激活函数和Leaky ReLU激活函数进行迁移学习得到近似的二次关系;最后在隐藏层8与8′采用SELU激活函数将预测结果进行二次修正后输出预测压力场速度场,即为图4中速度场迁移学习和压力场迁移学习。其中,隐藏层7与7′、隐藏层8与8′之间没有直接联系,通过损失函数对两者输出计算反向误差,利用链式求导法则修正权重。每经过一次正向运算和反向运算为一个完整的训练过程。相比于采用两组独立神经网络的方法,本文使用迁移学习方法在不同的输出采用相同损失函数达到相互制约的目的,并且该方法在一次梯度下降过程中可以对两组输出进行反向修正,加速收敛,预测模型详细参数如表1所示。

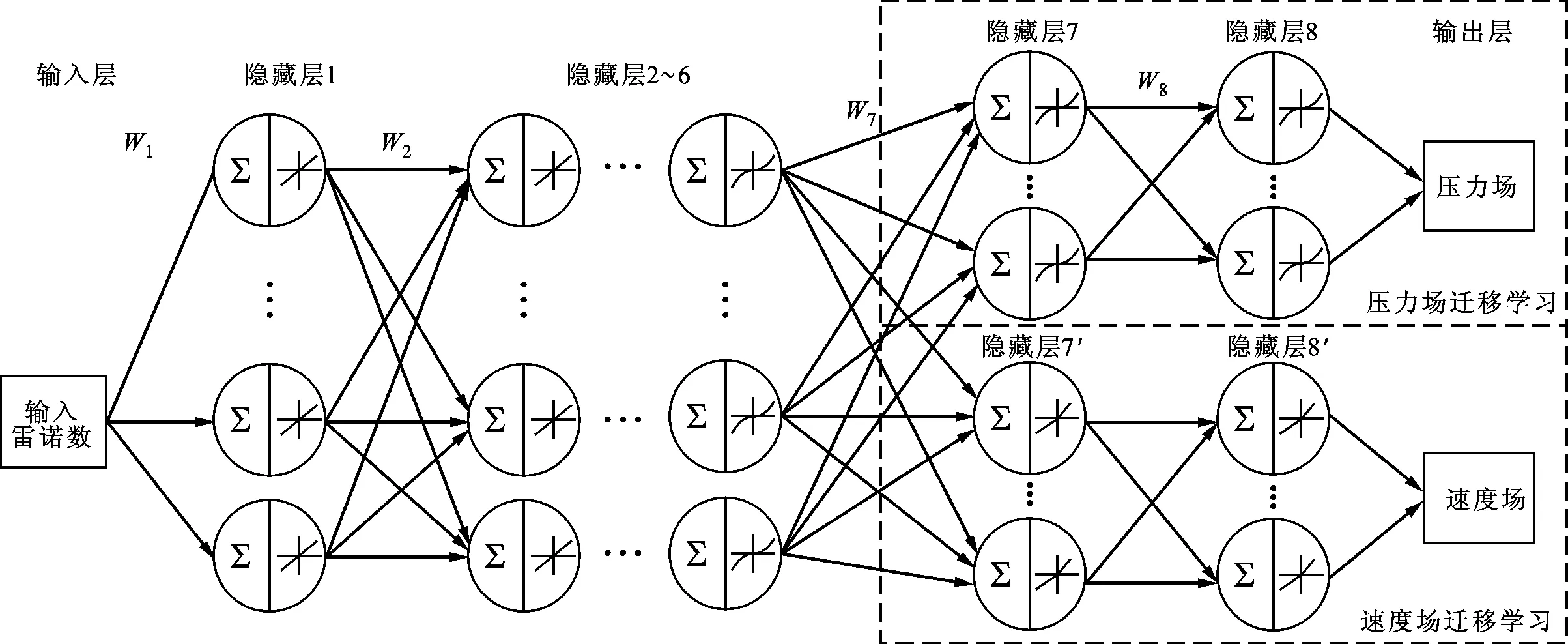
图4 神经网络结构

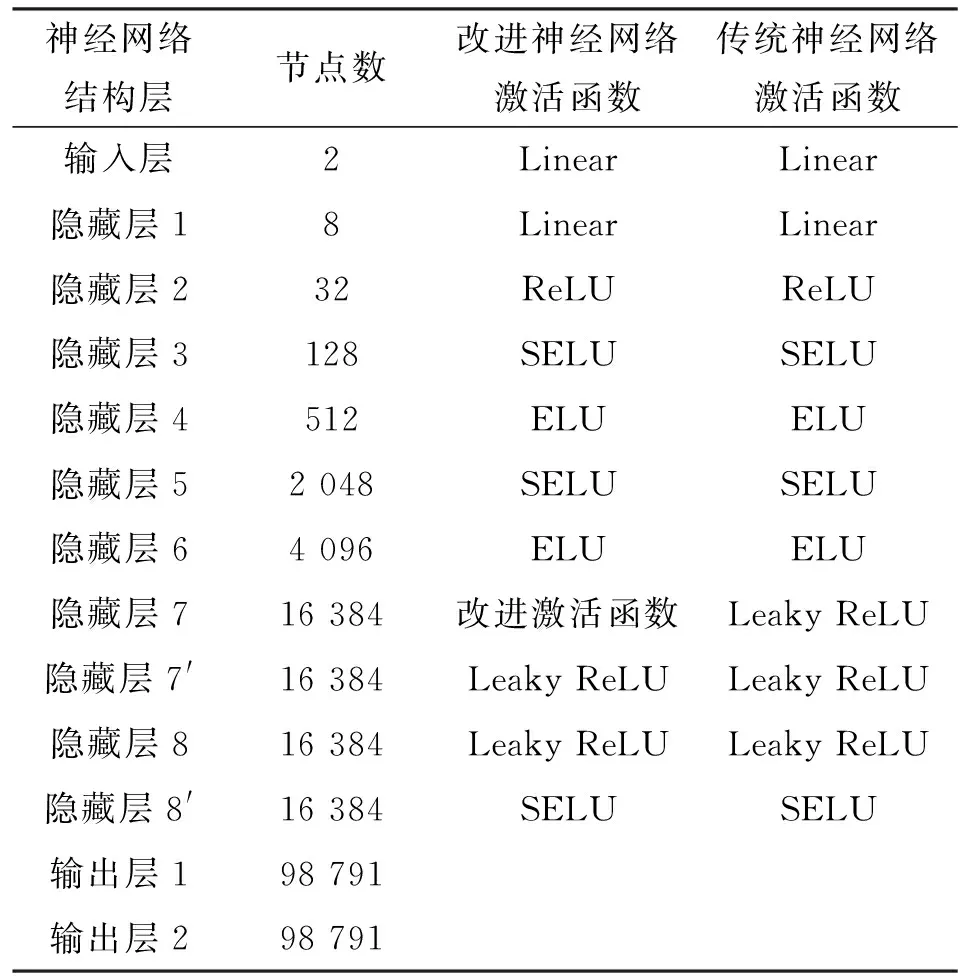
表1 神经网络结构参数

最后,采用全连接神经网络进行预测,优化器选用Adam[20],学习率初始值为0.000 7,每次按1%的速度衰减,训练总步数为500步,每批次输入22组包含雷诺数和攻角的列表及对应的压力场速度场数据,并通过梯度下降法逐步拟合流场参数,在神经网络中采用L2正则化方法预防过拟合。在训练完成后进行预测,保存预测的流场数据与网络模型,以达到重复利用的目的。

2 预测结果分析

通过神经网络可以计算得到翼型压力场、速度场分布如图5、图6所示。

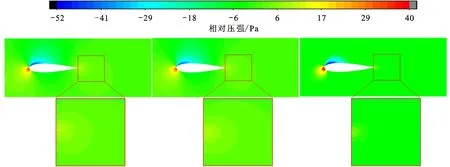
(a)传统激活函数神经网络 (b)改进激活函数神经网络 (c)数值模拟结果 预测结果 预测结果图5 α=4°、Re=0.55×106时压力场真实样本与神经网络预测结果误差分析

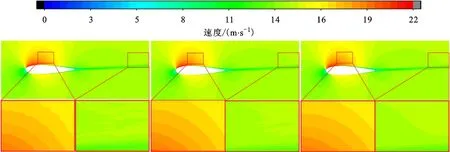
(a)传统激活函数神经网络 (b)改进激活函数神经网络 (c)数值模拟结果 预测结果 预测结果图6 α=4°、Re=0.55×106时速度场真实样本与神经网络预测结果误差分析

图5为α=4°、Re=0.55×106下的翼型附近压力场对比云图,通过对比翼型绕流压力场可知,压力最大值出现在翼型表面迎风驻点处,与之相对在上翼面距前缘约0.1C位置出现低压区,并出现轻微的流动分离。在翼型后缘附近,上下翼面绕流在钝尾缘汇合,使得后缘附近的压力升高,与文献[14-15]结果一致,且在局部放大图中可以看出尾缘附近高压区的预测结果比真实样本大。这是因为尾缘附近流动不稳定,速度变化较剧烈,而神经网络的拟合为保证全局最优,导致在尾缘附近无法准确预测。

图6为α=4°、Re=0.55×106时的速度场云图,速度场预测结果误差较为明显,两种神经网络预测结果比真实样本略大。由图可以看到,在翼型上翼面部分神经网络预测的速度场过渡部分出现明显锯齿状分布,且传统神经网络锯齿状分布更加明显。这是由于上翼面附近速度较大,且该处速度变化较为剧烈,神经网络在该处难以适应流场剧烈变化而产生误差。通过改进激活函数,将压力与速度联立拟合可以获得较好的精度。此外,在距后缘约0.8C～1.5C的位置神经网络速度场预测结果出现条状分布,传统神经网络预测结果大幅度偏离真实样本趋势,而改进的神经网络预测结果虽然出现条状速度分布,但总体趋势与真实样本有类似的过渡趋势。其原因是在有攻角绕流中上下翼面绕流在后缘附近发生流动冲击,流动不稳定,速度变化剧烈,使神经网络拟合度降低。

通过对比翼型速度场及压力场云图可以发现,完全采用Leaky ReLU激活函数难以获得准确的压力场预测结果,采用改进激活函数时,能有效地降低速度场分布不均问题和速度云图的锯齿问题。

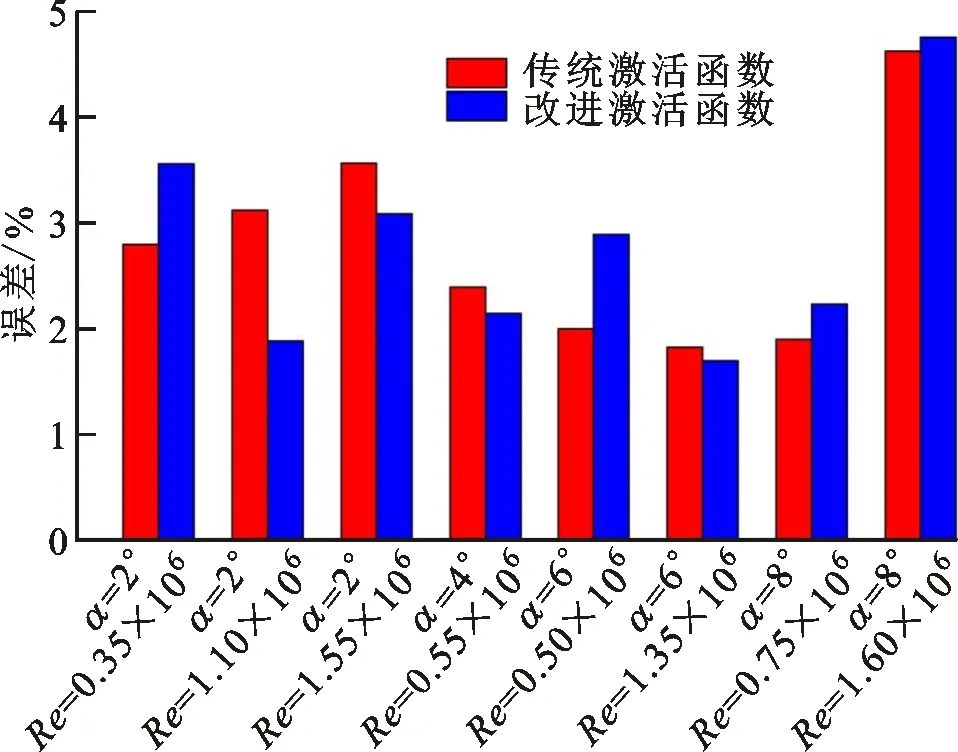
(a)压力场预测误差

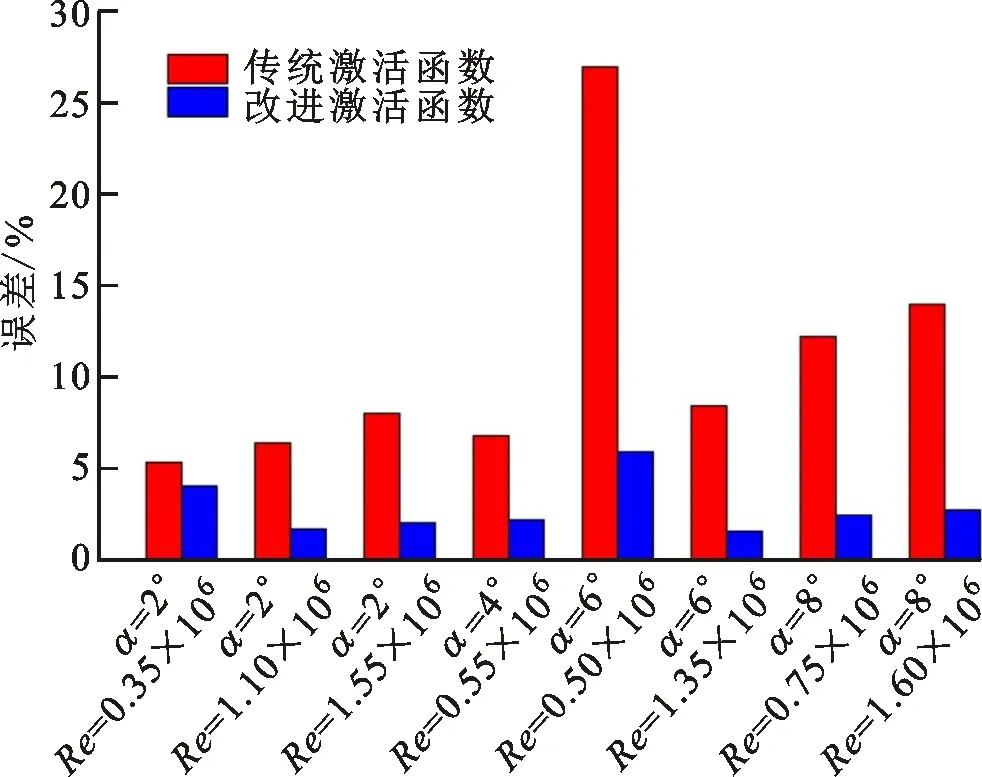
(b)速度场预测误差图7 两种神经网络的速度场和压力场误差

图7a、7b为随机抽取的8组数据下两种不同激活函数神经网络预测结果与真实样本之间压力场、速度场的平均误差。改进激活函数在所有攻角下压力场的预测中,平均误差分别为2.77%和2.782%,速度场平均误差分别为2.775%和11.01%;两种神经网络的最大误差均出现在α=6°、Re=0.5×106处,原因是该雷诺数下开始出现较大流动而不稳定,导致计算结果出现较大误差[21],神经网络对这一特殊流态的捕捉出现了较大偏差。

统计误差可得传统激活函数压力场、速度场误差分别为2.887%和1.995%,而传统激活函数的预测误差达到了26.993%。其原因是传统激活函数对压力场速度场的关系不能准确把握,场量之间没有任何约束,导致网络模型在速度场预测中出现较大误差,而速度场预测误差普遍比压力场大是因为翼型边界层速度接近于0,在计算相对误差时分母很小,导致误差较大。通过对比可得,相比传统激活函数,改进的激活函数在流场预测中具有更好的鲁棒性。

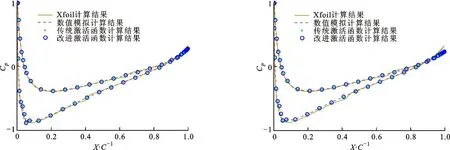
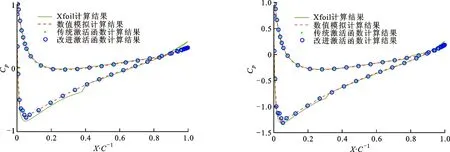
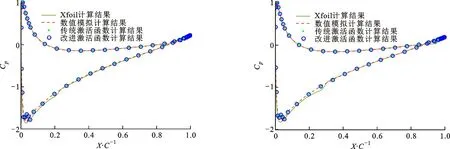
翼型表面压力系数直接决定翼型升阻力系数,提取部分预测结果和真实样本压力系数Cp进行对比,结果如图8所示。由图可知:驻点出现在翼型表面前缘点的下方,上翼面的压力系数在前缘点之后出现陡降,随后逐渐回升;下翼面压力系数从前缘点至驻点处急剧升高,并在驻点处达到最大值1,随后逐渐减小,与文献[14-15]结果一致;在后缘附近,上下翼面压力近似相等。由于翼型前缘点附近压力变化较大,真实样本表面压力系数出现波动[22],神经网络方法难以准确拟合,预测结果出现较大波动,引起较大误差。

将传统神经网络预测结果、改进神经网络预测结果、真实样本计算结果和Xfoil计算结果[23]对比,可以发现两种样本都与真实样本接近,但由于数值模拟未能准确计算出转捩位置,故神经网络未能学习这一过程。对比两种神经网络对表面压力系数的预测结果,采用改进激活函数神经网络可以更准确地获得表面压力系数,尤其在驻点附近和上翼面分离点到尾缘部分,原因是传统激活函数预测结果缺少相互约束,故传统激活函数预测结果具有较大偏差。

综合比较图8与表2、表3可以看出,改进神经网络在压力场、速度场的预测中效果更好,而传统神经网络在速度场预测中存在较大误差。这是因为在近壁面速度近似为0,而预测结果通常会有一定的绝对误差,从而产生较大的相对误差,但改进激活函数计算所得压力与速度相互修正,可得更好结果。

(a)α=2°,Re=0.35×106(b)α=2°,Re=1.1×106

(c)α=2°,Re=1.55×106(d)α=4°,Re=0.55×106

(e)α=6°,Re=0.5×106(f)α=6°,Re=1.35×106

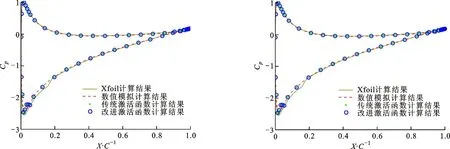
(g)α=8°,Re=0.75×106(h)α=8°,Re=1.6×106图8 不同雷诺数下翼型上下翼面压力系数对比

表2 改进激活函数与传统激活函数神经网络压力预测误差对比

表3 改进激活函数与传统激活函数神经网络速度预测误差

表4通过对比CFD与神经网络的计算时长,可以发现,在相同条件下,CFD计算时长以h为单位,训练完成的神经网络计算时长以s为单位。神经网络计算时长与传统CFD方法相比减少至少两个数量级。

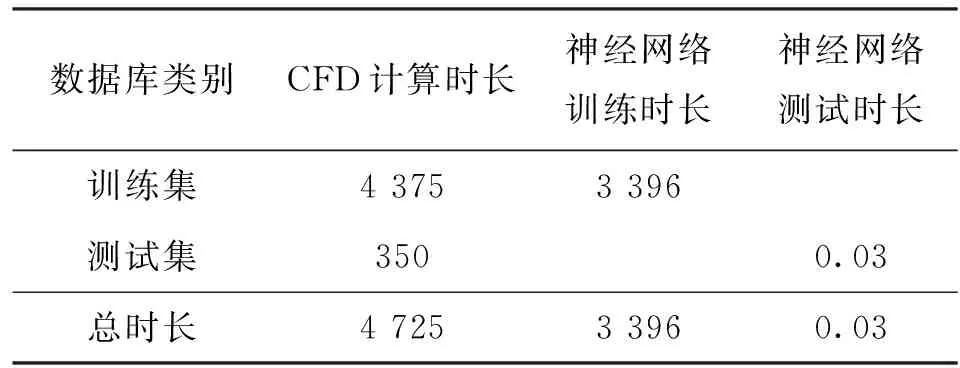
表4 CFD与神经网络计算时长对比 min

3 结 论

本文基于改进的全连接神经网络预测NACA0018翼型在Re=0.1×106～1.6×106下的压力场和速度场,将能量守恒方程与深度学习方法相结合,构造新的激活函数,采用多任务学习思想来约束速度场、压力场计算的结果,得到雷诺数与流场参数的映射关系。通过对比CFD计算结果,验证改进激活函数的神经网络对不同雷诺数下流动状态预测的泛化能力和模拟精度,得到结论如下。

(1)利用全连接神经网络能够复现Re=0.1×106～1.6×106下翼型的压力场与速度场,对比真实样本发现,改进激活函数的神经网络在流场预测中具有更好的鲁棒性。

(2)在网络采用正则化方法的前提下,改进激活函数神经网络相比常规激活函数神经网络在翼型表面的压力场与速度场预测中有更高的准确度,尤其在容易出现误差的近壁面处,改进激活函数的神经网络能够更准确地预测流场。

(3)经过一次训练保存的神经网络无需二次训练即可以反复调用并预测一定范围的翼型流场,相比翼型流场数值模拟,神经网络方法可以通过学习准确的CFD数据或实验复现流场,其计算时长与传统CFD方法相比,花费时间从h降低到s,大大提高了计算效率。