涡轮叶片厚壁带肋通道冷却性能的实验研究
2021-03-08席雷徐亮高建民赵振李云龙
席雷,徐亮,2,高建民,赵振,李云龙
(1.西安交通大学机械制造系统工程国家重点实验室,710049,西安;2.广东顺德西安交通大学研究院,528300,广东佛山)
燃气轮机的循环热效率和输出功率的不断提高,使得叶片面临越来越严重的热问题,迫切需要发展高效的叶片冷却技术进行热防护[1]。
肋片扰流冷却通过肋片的扰流作用增强通道的传热性能,被广泛地应用于燃机叶片的中弦区域[2]。Ghorbani等对不同阻塞比的带肋通道的传热特性进行了数值研究,指出高阻塞比有效地提高了冷却通道充分发展区域的传热性能[3]。Ayli等对方形带肋通道内的强迫对流传热进行了研究,拟合得到了有关雷诺数、肋间距和肋片宽高比的传热关联式[4]。Siddique等研究指出,45°带肋通道的摩擦系数和平均努塞尔数均随着通道宽高比的增大而增大[5]。Yang等实验研究了高阻塞比带肋通道的传热特性,指出肋间距比为10时传热最佳[6]。Chung等实验研究了不同宽高比矩形通道的传热性能,指出倾斜肋片通道的传热性能随着高宽比的增大而下降[7]。Ravi等研究发现,V型肋和45°斜肋的综合热力性能较优[8]。Liu等指出,截断肋可以在不降低带肋通道传热性能的情况下减少压力损失[9]。Lin等研究指出在相同的工况下,楔形带肋通道的平均努塞尔数比矩形带肋通道提高了约25%~32%[10]。张志强研究指出增大肋角、肋宽和减小肋间距可以提高通道的传热性能,但同时也增加了通道的压力损失[11]。王晋声通过调整肋角来改善带肋通道前缘侧传热差的现象,指出当肋角为45°时传热效果最优[12]。杜明杰采用大涡模拟对带肋通道内的流动和传热机理进行了数值研究,给出了近壁面湍动能与壁面传热系数之间的关联式[13]。
上述文献都是针对薄壁带肋通道冷却进行的研究,而针对具有三维导热效应的厚壁带肋通道的研究还比较匮乏。Young等研究指出,为准确分析扰流冷却通道的传热特性,在实验和数值研究中都需要添加具有一定厚度的金属壁面,以接近涡轮叶片实际的应用环境[14]。Han等的初步研究结果表明,厚壁带肋通道和薄壁带肋通道的壁面温度分布和传热系数分布均有较大差异[15-16]。Cukurel等研究指出,纯对流计算中的热边界条件是不真实的,耦合传热分析为准确模拟真实发动机叶片的传热情况提供了机会[17]。Coletti等采用纯流体域计算方法和流固耦合传热方法对带肋通道的传热性能进行了数值计算,发现两种计算方法对壁面平均努塞尔数的预测结果相差25%[18]。迟重然等的研究表明,厚壁带肋通道具有非常明显的耦合传热效应[19]。Xu等通过实验结合数值模拟的方法,量化了厚壁带肋通道实验测试系统的热损失率[20]。本课题组前期采用数值模拟对厚壁带肋通道的流动、传热性能进行了单参数分析[21-22],但并未采用实验方法分析多个参数对带肋通道冷却性能的综合影响规律。
本文实验研究了涡轮叶片厚壁带肋通道的冷却性能,研究参数包括宽高比W/H(0.25~4)、肋角α(30°~90°)和雷诺数Re(10 000~60 000)。与文献[21-22]相比,本文的创新点在于:研究了通道宽高比和肋角这两个参数同时对空气冷却厚壁带肋通道的综合影响规律,得到了基于传热系数最大和综合热力系数最大的最优宽高比和肋角的范围;根据传热系数随雷诺数、宽高比、肋角的实际变化规律,拟合了相应形式的经验关联式。

图1 带肋通道实验系统图
1 实验装置
1.1 实验系统
单元带肋通道空气冷却实验系统如图1所示,其主要由空压机、空气加热器、实验通道、短路加热器、排气装置以及数据采集系统等组成。该实验系统可以提供温度为0~250 ℃、压力为0.1~0.7 MPa、最大流量为3 kg·s-1的冷却空气。冷气经整流段后流入实验通道并对其进行冷却,最后经消音器排向大气。
进行实验时,将短路加热器的正负电极直接固定在实验通道的两端,采用0~7.5 V的低电压和0~4 500 A的大电流对通道壁面的加热量进行调节。实验通道和相邻管道包裹100 mm厚硅酸铝纤维纸,导热系数为0.035 W·m-1·K-1,以减少实验的热损失。
1.2 实验通道
10种通道均模化于某涡轮叶片内冷通道。图2给出了实验件的结构示意图。带肋通道由4块304不锈钢板焊接而成,常温下密度为7 930 kg·m-3,导热系数为15 W·m-1·K-1,比热容为502 J·kg-1·K-1。其中,光滑壁面为3 mm厚的不锈钢板,带肋壁面由6 mm厚的不锈钢板经过铣削加工而成,长度L为1 000 mm。
在图2中,通道进口处z/D=0,其中D为通道当量直径。实验通道的宽高比变化范围为0.25~4,在通道宽度侧的两个对应壁面上等间距布置了多个方形截面的扰流肋片,肋间距比P/e恒定为10,肋角变化范围为30°~90°。表1列出了10种实验通道的详细结构参数。
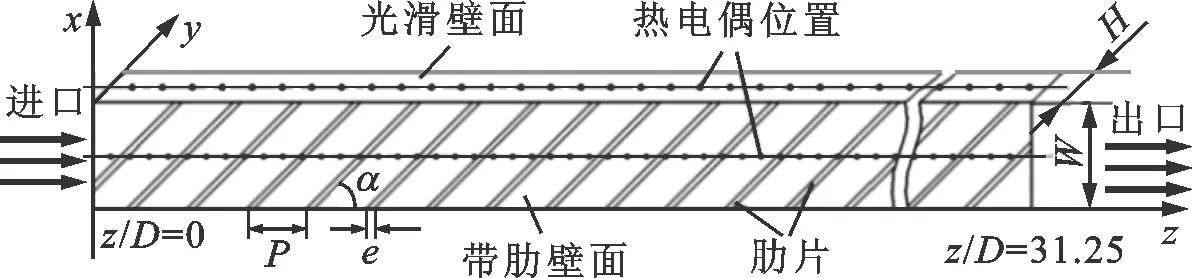
(a)结构参数

(b)实物图图2 实验通道结构示意图

表1 实验通道结构参数
实验通道进、出口分别放置了两个直径为3 mm、精度为±0.4%的E型热电偶,用于测量进、出口冷气温度。通道外壁面沿中心线上焊接了90个直径为0.5 mm的E型软体热电偶,其中带肋面侧61个,光滑面侧29个,用于测量通道壁面温度并计算其传热系数,热电偶精度同样为±0.4%。通道进、出口的压力以及进口流量分别由精度为±0.075%的绝压变送器(NCS-PT105Ⅱ SA)和精度为±2%的流量计(QWLU-DN80)测得。
1.3 数据处理
雷诺数可以由下式计算得出
Re=ρuD/μ
(1)
式中:ρ为冷气密度;u为通道进口冷气平均速度,由测得的质量流量计算得出;μ为冷气的动力黏度。
实验通道内壁面的热流密度
q=(Qh-Qloss)/Sin
(2)
式中:Qh为短路加热器的输出功率;Sin为实验通道内壁面面积;Qloss为散热损失,经过计算,本文实验的最大热损失约为总加热量的8.83%。
壁面当地努塞尔数
Nu=qD/(Tw-Tf)λ
(3)
式中:Tw为热电偶测量的通道壁面温度;Tf为参考温度;λ为冷气的导热系数。
Tf由通道进、出口平均温度经线性插值来获得
Tf=Tin+(Tout-Tin)z/L
(4)
式中:z为温度测点到实验段进口的距离;Tin为通道进口平均温度;Tout为通道出口平均温度。
通道的摩擦系数可以定义为
f=ΔpD/2ρLu2
(5)
式中:Δp为通道进、出口之间的压差。
(6)
经计算,本实验测量的带肋通道进口雷诺数、努塞尔数和摩擦系数的最大不确定度分别为3.6%、8.8%和6.3%。
2 结果分析与讨论
具体的实验工况如下:通道进口空气的压力和温度分别为0.3 MPa和445 K,进口雷诺数为10 000~60 000,壁面热流密度约为5 kW·m-2。
2.1 流动特性分析
图3所示为实验测量的10种典型带肋通道进、出口压差和摩擦系数随雷诺数的变化规律。从图3a中可以看出,10种带肋通道的进、出口压差均随雷诺数的增大而增大,且随雷诺数的增大,压差的增速也变大。这是因为雷诺数的增大使得冷气在通道内的流动更加剧烈,从而产生更大的压力损失。同时,还可以发现,实验通道3的压力损失最大,其次为通道4,而通道9的压力损失最小。从图3b中可以看出,10种带肋通道的摩擦系数随雷诺数的分布规律各不相同,这一现象要从摩擦系数的定义上来分析。由式(5)可知,摩擦系数与通道进、出口压差成正比,而与通道进口冷气速度的平方成反比。因此,摩擦系数是由通道进、出口压差的变化以及通道进口冷气速度平方的变化共同决定的。当通道进、出口压差的增速大于通道进口冷气速度平方的增速时,摩擦系数随雷诺数的增大呈现出上升的趋势,如通道3和10等的摩擦系数在雷诺数较高时的分布趋势;当通道进出口压差的增速小于通道进口冷气速度平方的增速时,摩擦系数随雷诺数的增大呈现出下降的趋势,如通道4和7等。从图中还可以发现,10种典型带肋通道中,通道3和10的摩擦系数较高,流动性能较差,通道5和6的摩擦系数较低,流动性能较好。

(a)压差分布
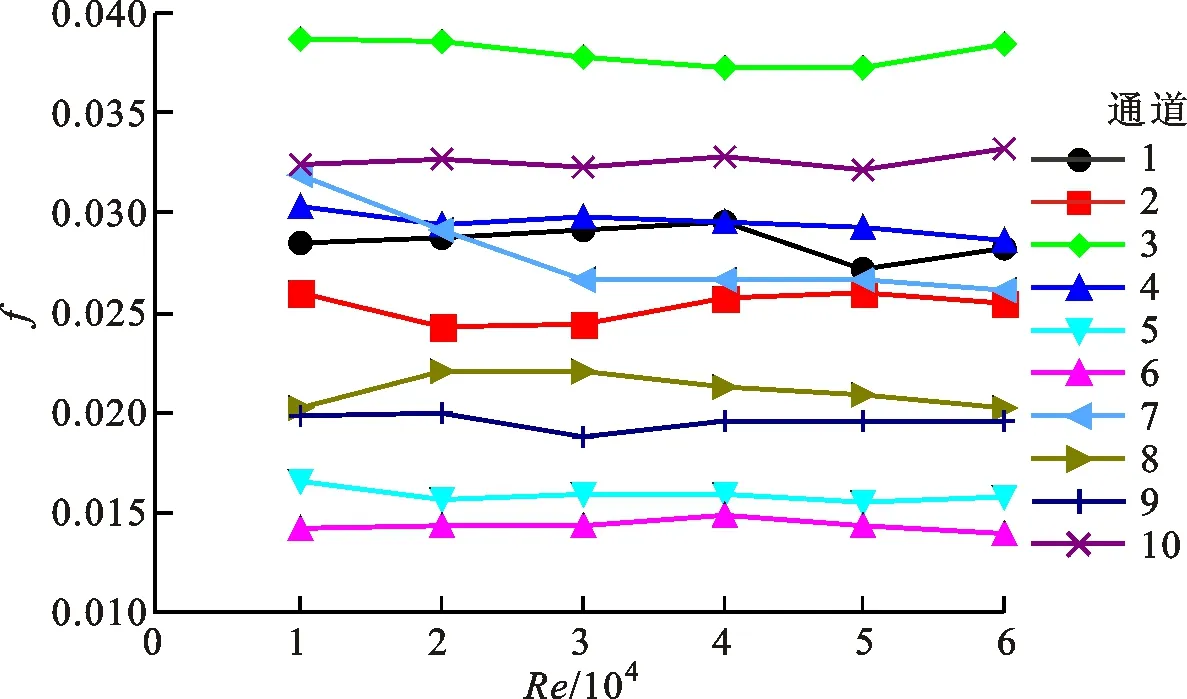
(b)摩擦系数分布图3 压差和摩擦系数随雷诺数的变化
图4所示为雷诺数分别为30 000和60 000时通道摩擦系数的等高线图。从图4中可以看出:不同雷诺数时,通道摩擦系数随W/H的增大呈现出升高的趋势;当W/H较小时,通道摩擦系数随肋角大致呈现出先增大后又略微减小的分布趋势;当W/H较大时,摩擦系数随肋角呈现出增大的趋势。从图中大致可以发现,在高雷诺数情况下,W/H约为0.25、α约为30°时通道的摩擦系数最小,而W/H约为4、α约为45°时通道的摩擦系数最高。

(a)Re=30 000
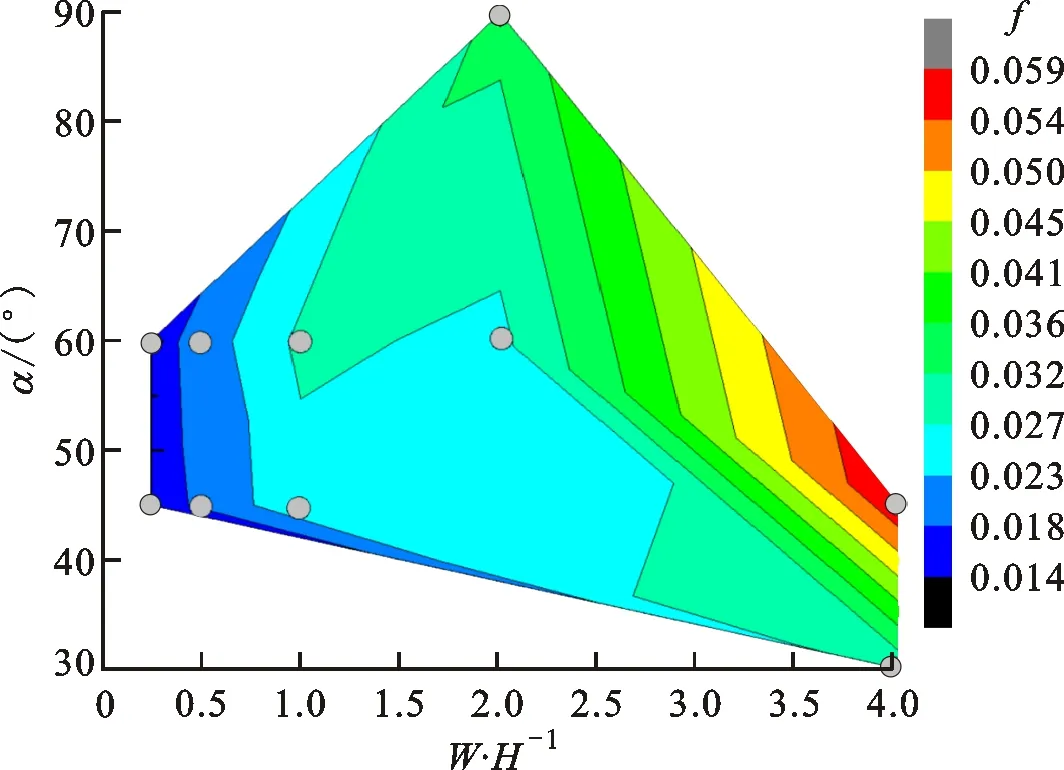
(b)Re=60 000图4 不同雷诺数时摩擦系数的等高线图
2.2 传热特性分析
图5给出了厚壁带肋通道7的轴向壁面温度、进出口冷气温度以及轴向当地努塞尔数的分布特征。从图5a和5b中可以看出,冷气温度从通道进口到出口逐渐增大,表明了冷气被不断地加热。典型的温度分布,即通道带肋壁面和光滑壁面上的当地温度在z/D<4的未充分发展区域内均沿着通道轴向快速地升高,而在z/D>4的区域内则缓慢地升高,这是因为冷气穿过通道时被不断加热的缘故。与Han等研究的薄壁通道壁面当地温度沿轴向周期性波动的分布趋势[8]不同,本文厚壁通道当地壁面温度沿轴向的分布接近于光滑曲线,而并没有明显的波动。这是因为实验测量的通道外壁面温度是一种平均温度,它受到了通道壁面厚度方向、轴向和径向等3个方向的导热效应(即三维导热效应)的影响。从图5c中可以看出,带肋侧和光滑侧壁面当地Nu在z/D<4的未充分发展区域内均沿通道轴向快速地降低,随后在z/D>4的区域内则基本保持不变。可见,通道内流体在z/D>4的区域内达到了周期性的充分发展状态。此外,同样是由于厚金属壁面的三维导热效应,本文厚壁通道壁面当地Nu沿通道轴向的分布也接近于光滑曲线,而没有表现出如Han等发现的薄壁通道当地Nu沿轴向呈现出的周期性“拱形”波动现象[8]。

(a)当地温度分布(Re=30 000)

(b)通道进出口线性温度分布(Re=30 000)
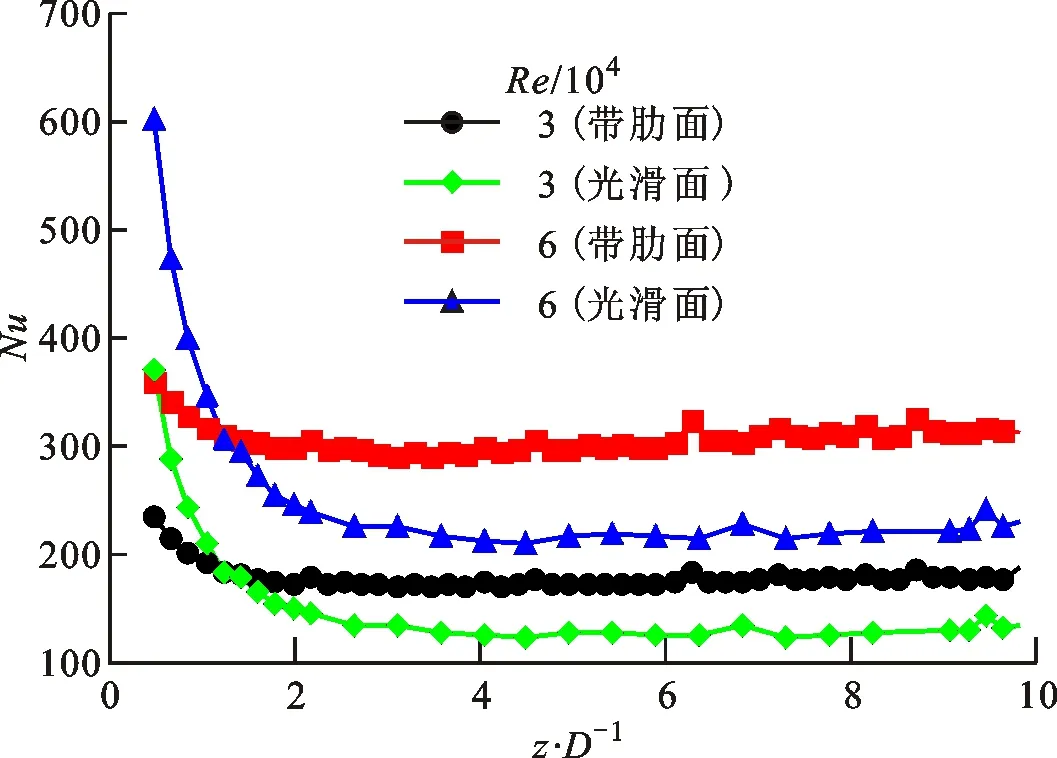
(c)当地努塞尔数分布图5 通道7的壁面温度、流体温度和当地努塞尔数分布
本文采用由实验测量的带肋壁面和光滑壁面的当地努塞尔数计算得出的平均努塞尔数来评估带肋通道的传热性能。图6给出了10种典型带肋通道壁面平均努塞尔数随雷诺数的变化规律。从图中可以看出,10种典型带肋通道壁面平均努塞尔数随雷诺数的变化趋势相同,即随着雷诺数的增大而增大。这是因为雷诺数的增大增强了通道中心冷流体与壁面附近热流体之间的热量交换而造成的。在10种典型带肋通道中,雷诺数较低时,通道7的平均努塞尔数最高,传热性能最佳,其次为通道2、3、8和9,通道5、6和10的平均努塞尔数最低,传热性能最差;雷诺数较高时,通道7、8和9的平均努塞尔数最高,传热性能最佳,通道5、6和10的平均努塞尔数依然最低,传热性能最差。总体来讲,不同雷诺数时,通道7是10种实验通道中传热性能最佳的通道。

图6 平均努塞尔数随雷诺数的变化

(a)Re=30 000

(b)Re=60 000图7 不同雷诺数时的平均努塞尔数的等高线图
图7所示为雷诺数分别为30 000和60 000时通道壁面平均努塞尔数的等高线图。从图中可以看出:不同雷诺数时通道壁面平均努塞尔数的等高线图呈现出了相似的图案,即图案中心红色区域的平均努塞尔数值最高,图案边缘区域平均努塞尔数值较低;通道壁面平均努塞尔数在研究范围内随着肋角先增大后减小,而随着宽高比在W/H=0.25~1和W/H=1~4的区间内都呈现出先增大后减小的趋势。总的来说,不同雷诺数时壁面平均努塞尔数的最大值都大致出现在W/H为1.75~2.75、α为55°~65°的区间。
2.3 综合热力性能分析
图8所示为10种带肋通道的综合热力系数随雷诺数的变化曲线。从图8中可以看出,10种带肋通道的综合热力系数均随着雷诺数的增大而增大,即雷诺数可以有效提高带肋通道的综合热力性能。同时,还可发现:在低雷诺数时,通道7、2、8和9的综合热力性能最佳,通道3、4和10的综合热力性能最差;在高雷诺数时,通道7、8和9的综合热力性能最佳,通道3、4和10的综合热力性能依然最差。出现这样分布规律的原因是不同通道的摩擦系数和平均努塞尔数随着雷诺数的变化趋势不同所造成的。综合来看,不同雷诺数时,通道7的传热性能和综合热力性能均最佳。

图8 综合热力系数随雷诺数的变化
图9所示为雷诺数分别为30 000和60 000时通道综合热力系数的等高线图。从图中可以看出,不同雷诺数时,通道的综合热力系数随着肋角的增大均表现为先增大后减小的分布趋势,而随着宽高比的增大表现为先增大后减小、再增大再减小的分布趋势。同时可见,不同雷诺数时,最高的综合热力系数出现在W/H约为0.75和2、α约为60°时。

(a)Re=30 000

(b)Re=60 000图9 不同雷诺数时综合热力系数的等高线图
2.4 关联式拟合
厚壁带肋通道的传热和摩擦关联式对于指导未来重型燃机涡轮叶片冷却结构设计具有重要的意义。本研究采用Python拟合带肋通道的传热和摩擦关联式,冷气的Pr保持为恒定值0.697。首先对10种带肋通道的摩擦系数和平均努塞尔数分别进行雷诺数相关的幂函数拟合,如下式所示
(7)
f=C2Rem2
(8)
通过对式(7)(8)进行对数变换,并利用最小二乘法将10种典型带肋通道的传热、摩擦关联式分别拟合,得到的系数C1、m1和C2、m2拟合结果列于表2之中,确定系数R2均大于0.9。本小节还拟合了同时反映雷诺数、宽高比和肋角对带肋通道传热系数和摩擦系数影响的经验关联式。基于2.1~2.3小节中的分析,建立了如下形式的关联式
[a6α2+a7α+a8]
(9)
f=b1Reb2(W/H)b3αb4
(10)
以60组实验数据为样本,采用Python中的非线性拟合模块Curve_Fit进行非线性函数拟合,得到的表达式如下

(11)
f=0.012 5Re-0.012 2(W/H)0.406α0.209
(12)
式(11)(12)的适用范围为:10 000≤Re≤60 000;0.25≤W/H≤4;30°≤α≤90°。

表2 C1、m1和C2、m2的拟合结果
图10给出了拟合的偏差分布:对于传热关联式,最大偏差为-17.79%,平均偏差为6.96%,拟合公式的确定系数R2=0.923;对于摩擦关联式,最大偏差为31.14%,平均偏差为12.75%,拟合公式的确定系数R2=0.901;由传热关联式和摩擦关联式推导而来的综合热力系数的最大偏差为22.21%,平均偏差为7.03%。

(a)传热关联式偏差
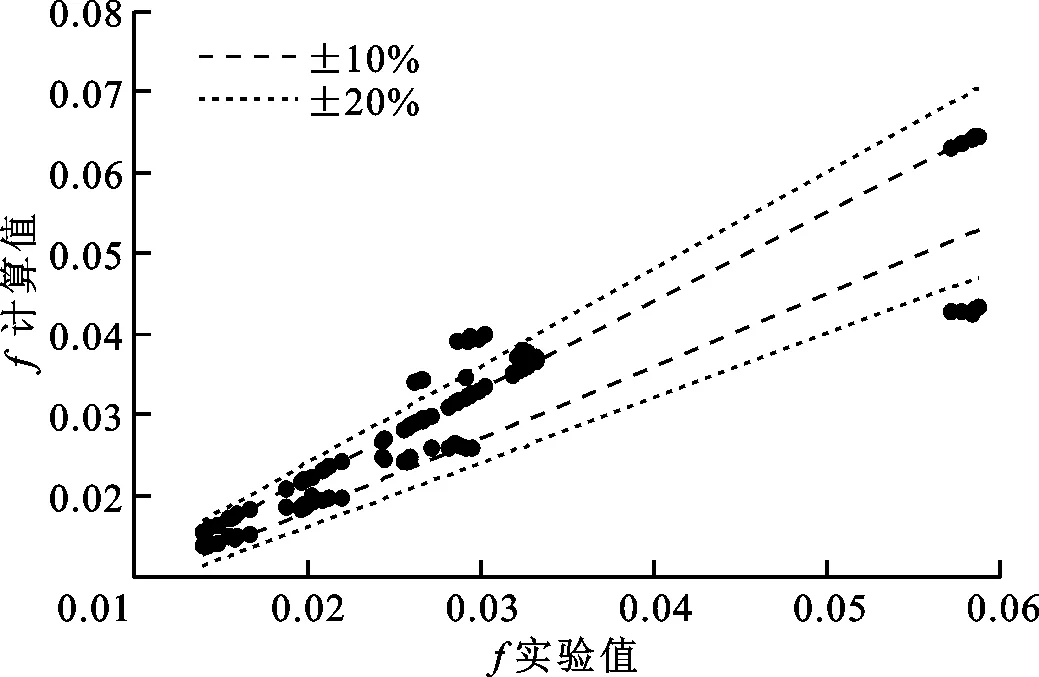
(b)摩擦关联式偏差

(c)综合热力系数偏差图10 非线性公式拟合偏差分布
3 结 论
本文通过实验方法研究了10种典型厚壁带肋通道的流动及传热性能,得到如下主要结论。
(1)在研究范围内,带肋通道摩擦系数随宽高比和肋角的增大均大致呈现出升高的变化趋势,平均努塞尔数和综合热力系数随肋角的增大均表现为先增大后减小的分布趋势,随宽高比的增大表现为先增大后减小、再增大再减小的分布趋势。
(2)不同雷诺数时,壁面平均努塞尔数的最大值都大致出现在W/H为1.75~2.75、α为55°~65°的区间;最高的综合热力系数出现在W/H约为0.75和2、α约为60°时。
(3)拟合得到了平均努塞尔数和摩擦系数关于进口雷诺数、宽高比和肋角的经验关联式,其中:平均努塞尔数关联式的最大拟合偏差为-17.79%,平均拟合偏差为6.96%;摩擦关系数联式的最大拟合偏差为31.14%,平均拟合偏差为12.75%。
(4)拟合得到的厚壁带肋通道的传热和摩擦关联式,可以为未来先进燃气轮机涡轮叶片内冷通道冷却结构的设计提供参考。
