操作系统病毒时滞传播模型及抑制策略设计
2021-03-08王刚冯云马润年
王刚,冯云,马润年
(空军工程大学信息与导航学院,710077,西安)
操作系统病毒能利用操作系统漏洞攻击网络并在网络中传播,对网络及其用户造成重大损失。彻底查杀病毒需要消耗大量的时间和精力,难以在操作系统病毒入侵初期快速构建有效防御[1-3]。动态目标防御等新型防御手段[4-7]提供了主动防御的新思路,但考虑部署代价、对网络业务的负面影响等因素,在全网部署并持续运行成本过高。合理高效地部署防御并抑制操作系统病毒传播,已经成为网络安全领域亟待解决的问题。
计算机病毒传播研究借鉴了生物学病毒传播理论,经典病毒传播模型包括SI、SIR和SIRS等[8-11]。这些模型将网络抽象成图,以用户为节点,用户之间的联系为边,根据感染行为及用户对病毒的防御能力将节点划分为不同状态,研究不同状态之间的节点转化关系,通过动力学建模和稳定性分析推演网络中病毒可能的扩散规模。随着网络攻防对抗的升级,网络结构、病毒攻击机理、传播方式有新的特点,病毒传播模型和相关研究也出现了一些针对性改进[12-15]。一类是适应病毒传播特点,添加新的节点状态,修改状态转化关系,使模型更加契合病毒的传播模式,如SEIR、SEIQR等病毒传播模型;另一类则是考虑病毒传播过程中感染、免疫的耗时问题,在模型中添加时滞,研究带时滞的病毒传播模型[16-20]。通常而言,无时滞时病毒传播较为稳定,而时滞则可能造成网络中感染节点数的振荡,时滞病毒传播情况更复杂。
操作系统病毒利用的是特定操作系统的漏洞,通常只能在特定操作系统平台上运行,操作系统病毒传播主要受网络中多种类型操作系统和感染时滞等因素的影响。考虑操作系统病毒传播特性,本文主要研究操作系统病毒时滞传播模型及抑制策略,包括:①考虑网络中操作系统切换和感染过程耗时对操作系统病毒传播的影响,在SIRS病毒传播模型的基础上,引入新的状态和感染时滞,构建操作系统病毒的时滞传播模型;②研究网络在不同平衡点处的稳定性,分析网络消除病毒和出现分岔的条件,以及影响网络中感染节点规模和分岔的关键参数;③针对感染时滞造成的分岔问题,设计有感染时滞的操作系统病毒抑制策略;④仿真分析关键参数对操作系统病毒传播的影响和病毒抑制策略的有效性。
1 操作系统病毒时滞传播模型
按照计算机病毒传播机理,操作系统病毒扩散通常经历了侦察、传播和感染等阶段。侦察阶段,探查当前网段内有相应操作系统漏洞且未被感染的主机;传播阶段,病毒将用于传播的模块链接附着在正常程序中,随着正常程序的启动被加载入内存并执行,实现病毒的传播;感染阶段,操作系统病毒传播至用户计算机后,在造成危害之前需要完成侦查、复制和传播等工作,而后才会利用相应漏洞对用户造成危害。病毒感染由一系列行为组成,感染过程需要耗费一定时间,而这一过程中如果操作系统发生变化,则会导致目标和漏洞丢失,导致感染失败。为便于分析,做出如下假设:①网络中仅存在一种操作系统病毒,能感染主流操作系统OS-A;②感染过程耗时为τ,一旦被打断则感染失败。
在经典SIRS计算机病毒传播模型基础上,构建操作系统病毒传播的时滞SIRO模型,相应的节点状态转化关系如图1所示。

图1 节点状态转化关系
图1中:S表示易感状态,该状态下的节点可以被感染节点感染;I表示感染状态,该状态下的节点已经被病毒危害,且具备感染其他节点的能力;R表示免疫状态,该状态下的节点无法被感染;O表示节点安装了其他操作系统的状态,该状态下的节点同样无法被感染节点感染;Sτ(t)=S(t-τ),Iτ(t)=I(t-τ)状态的节点数,S(t)、I(t)分别表示t时刻易感、感染状态的节点数;k表示网络的平均度;φ表示易感节点获得免疫能力的概率;δ表示免疫节点丧失免疫能力的概率;dA表示OS-A切换到其他操作系统的概率;dO表示从其他操作系统切换到OS-A的概率;N表示网络中节点总数,在一段时间内保持稳定。易感节点在同感染节点通信过程中,可能被植入操作系统病毒,并在时间τ内被感染,β表示易感节点单位时间内被其相邻的一个感染节点植入病毒的概率,一个节点被注入病毒的概率与其周围的感染节点数有关,当感染率较低时,可近似认为该节点被植入病毒的概率与其周围的感染节点数是线性相关的,易感节点周围感染节点数不完全相同,在动力学方程构建过程中,可采用平均场理论[8],用βkI(t)/N代替易感节点被植入病毒的概率。操作系统切换会打断操作系统病毒的感染和持续,在时间τ内,被植入操作系统病毒的易感节点未发生操作系统切换的概率为(1-dA)τ,易感节点的平均感染概率为βkIτ(t)(1-dA)τ/N。运用微分动力学方法,构建操作系统病毒传播的时滞微分方程为
(1)
式中R(t)、O(t)分别为t时刻免疫、安装了其他操作系统状态的节点数。
令dS(t)/dt=0,dI(t)/dt=0,dR(t)/dt=0,dR(t)/dt=0,求解可得平衡点P0(S0,I0,R0,O0)和P1(S1,I1,R1,O1)
(2)
式中
I1={[dO(dA+δ)βk(1-dA)τ-(dA+dO)·
(dA+ω)(dA+δ+φ)]/[(dA+δ+ω)·
(dA+dO)βk(1-dA)τ]}N
(3)
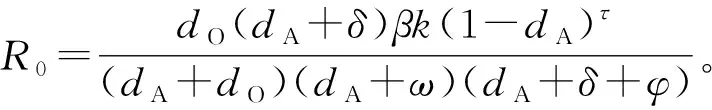
2 稳定性分析
设A(t)=S(t)+I(t)+R(t),式(1)可进一步表示为
(4)


(5)
相应的特征方程为
λ(λ+dA+dO)=0
(6)
由式(6)可得式(5)的两个特征根为λ1=0和λ2=-dA-dO,均为非正根。由劳斯稳定判据,式(6)在唯一平衡点处局部稳定。证毕。
引理2当t→∞时,S(t)≤S0。
证明由引理1可知,当t→∞时,有S(t)+I(t)+R(t)=dON/(dA+dO),进而可得R(t)=dON/(dA+dO)-S(t)-I(t),代入式(1)中dS(t)/dt可得
(7)
由微分方程比较定理可得
(8)

由于βkSτIτ(1-dA)τN-1+δI(t)≥0,所以S(t)≤S0。显然,当且仅当I(t)=I(t-τ)=0时,S(t)≤S0中的等号成立。证毕。
定理1当R0≤1时,式(1)表示的网络系统在无病毒平衡点P0(S0,I0,R0,O0)处全局渐进稳定。
证明定义Lyapunov函数
(9)
对式(9)求导可得
(10)
由引理2和式(2)可知
f′(t)≤I(t)(ω+dA)(R0-1)
(11)
当R0≤1时,f′(t)≤0,当且仅当I(t)=0时等号成立。根据LaSalle不变原理,式(1)表示的网络系统在无病毒平衡点P0(S0,I0,R0,O0)处全局渐进稳定。证毕。
定理2当R0>1时,存在τ0,使得当τ<τ0时,式(1)表示的网络系统在有病毒平衡点处局部渐进稳定,当τ≥τ0时,式(1)表示的网络系统在有病毒平衡点处振荡,出现Hopf分岔现象。
证明根据引理1,式(1)可简化为
(12)
对应的特征方程为
λ2+(n1+n3)λ+n1n3+
[(m1-m2)λ+m1n3-m2n1+m1n2]e-λτ
(13)
式中
(14)
令λ=iμ,利用欧拉公式,式(13)可化为
h(λ)=-μ2+c2+c3μsin(μτ)+c4cos(μτ)+
[c1μ+c3μcos(μτ)-c4sin(μτ)]i
(15)
式中
(16)
分离式(15)的实部和虚部,可得
(17)
进而可得
(18)
当R0>1时,式(18)有正根μ0,式(13)存在一对共轭复根±μ0i,结合式(17)可得
(19)
根据Hopf分岔理论可知:当τ<τ0时,式(1)表示的网络系统在有病毒平衡点处局部渐进稳定;当τ≥τ0时,式(1)表示的网络系统在有病毒平衡点处振荡,出现Hopf分岔现象。证毕。
由本节稳定性分析可知:①基本再生数是操作系统病毒持续存在的阈值,当R0≤1时,网络能够靠自身免疫能力和操作系统切换消除操作系统病毒;当R0>1时,无论是否出现分岔现象,操作系统病毒总能持续存在;②操作系统病毒在传播过程中的攻击过程耗时对其传播有两方面影响,一方面,攻击过程耗时越长,被操作系统切换打断的概率就越大,感染成功率越低,另一方面,攻击过程耗时导致感染节点数出现振荡,不利于用户或网络管理员对当前网络安全环境做出正确判断。
对于存在感染时滞的操作系统病毒,操作系统切换对操作系统病毒传播的影响体现在3个方面:①操作系统切换使部分感染节点中的操作系统病毒失去运行环境,从而无法运行;②操作系统的切换会打断感染过程,降低易感节点被感染的概率;③操作系统切换频率决定着网络中两类操作系统的比例,OS-A的数量越少,感染节点数也越少。
3 操作系统病毒抑制策略
抑制网络中操作系统病毒的传播,需要重点解决2个问题:①调整的度,现有平台动态目标防御技术虽然能实现异构平台之间的数据、应用迁移,但是非自发的操作系统切换会同步导致用户业务的损失,相关技术的部署和实施需要付出额外的成本,因此需要把握操作系统切换的度,尽量避免过高频率的切换;②当R0>1且τ>τ0时,网络系统在有病毒平衡点处振荡,出现Hopf分岔现象,网络环境安全状态难以判决,也无法根据网络安全状态实施针对性防御。本节结合基本再生数和稳定性分析,设计基于操作系统切换频率调整的病毒抑制策略。
操作系统切换频率参数dA和dO都能影响操作系统病毒的规模。其中,调整dO仅改变了网络中不同操作系统所占的比例,而调整dA则能加速感染节点平台的切换,使感染过程更大概率被打断以及改变不同操作系统的比例,本文通过调整dA抑制操作系统病毒传播。根据定理1,当R0<1时,网络能消除操作系统病毒,则参数dA需要满足
dO(dA+δ)βk(1-dA)τ-
(dA+dO)(dA+ω)(dA+δ+φ)<1
(20)
当R0>1且τ>τ0时,感染节点数存在振荡,难以估计网络中的感染节点数,因此首先需要设法消除这种振荡,对网络安全环境进行估计,然后再根据式(20)计算抑制操作系统病毒传播所需的参数配置。由定理2的证明过程可知,τ0与操作系统切换频率相关,在抑制操作系统病毒传播过程中,可先对参数dA进行小幅度调整并实时监测网络中病毒传播情况,一旦感染节点数相对稳定,则根据当前病毒传播情况进一步调整相关参数。基于此分析,设计抑制操作系统病毒传播的流程如下。
输入:微调值m,振荡判定阈值ΔI,反馈时间ΔT。
步骤1 获取一段时间(ΔT)内网络中感染节点数。
步骤2 如果该时段内感染节点数的极差大于ΔI,则认定存在振荡,采取步骤3,否则采取步骤4。
步骤3 若ΔT内网络中感染节点数的极差大于ΔIN,则认为仍存在振荡行为,dA=dA+m,返回步骤1。
步骤4 若ΔT内网络中感染节点数的极差不大于ΔIN,则认为感染节点数基本稳定,根据当前感染节点数,估计参数,根据式(20)计算消除病毒所需阈值。
步骤5 选取恰当的dA,对网络进行调整,直至网络恢复至安全状态。
4 仿真分析
通过仿真测试时滞τ和切换频率dA对病毒传播的影响,验证所提病毒抑制策略的有效性。设基本参数如下:N=2 000,k=16,ω=0.08,dA=0.01,dO=0.09,δ=0.1,φ=0.2。设单位时间为h,根据式(1)所示动力学方程模拟病毒传播过程的节点数变化时,会出现节点数为小数的情况,考虑实际病毒传播过程中,网络任意状态节点数均为整数,仿真结果中对节点数均做整数化处理。
4.1 时滞对病毒传播的影响
令β=0.015,对任意的感染时滞τ,均有R0<1,根据定理1,网络在无病毒平衡点处全局渐进稳定。β=0.015时,不同感染时滞下感染节点数的变化曲线如图2所示。可以看出,当R0<1时,感染时滞仅造成感染节点数变化上的延迟,尽管不同时滞下的感染节点数变化趋势不同,但网络最终能够在无病毒平衡点处达到稳定。

图2 β=0.015时不同感染时滞下感染节点数的变化曲线

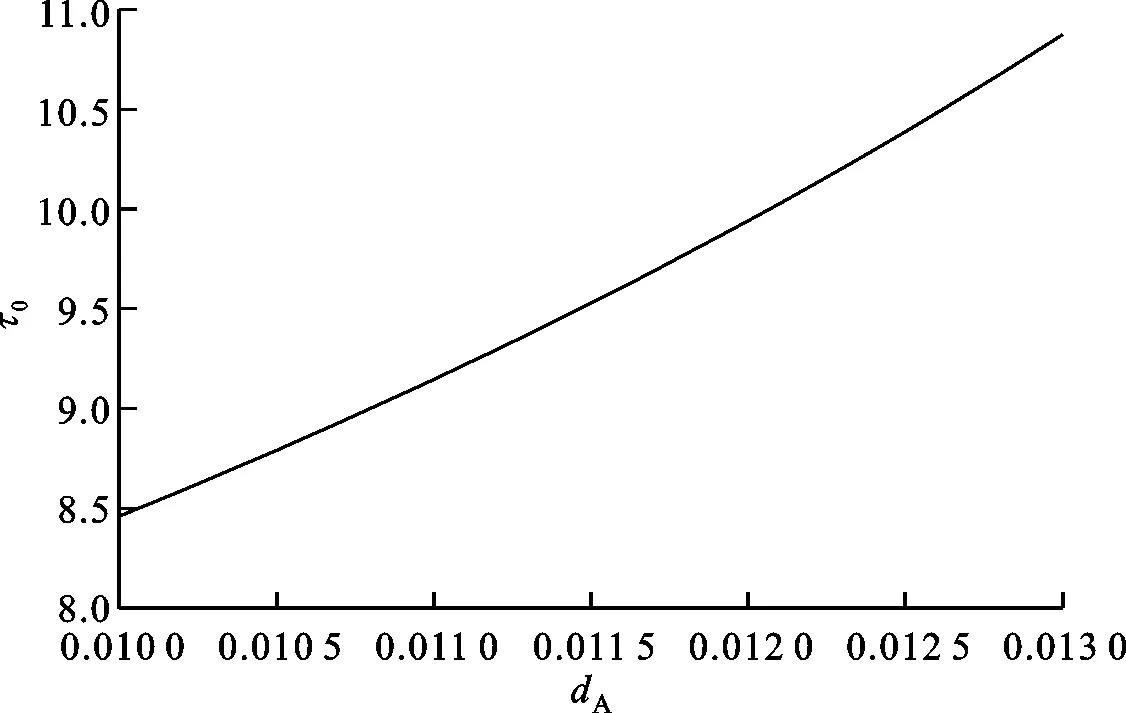
图3 τ0随τ的变化曲线
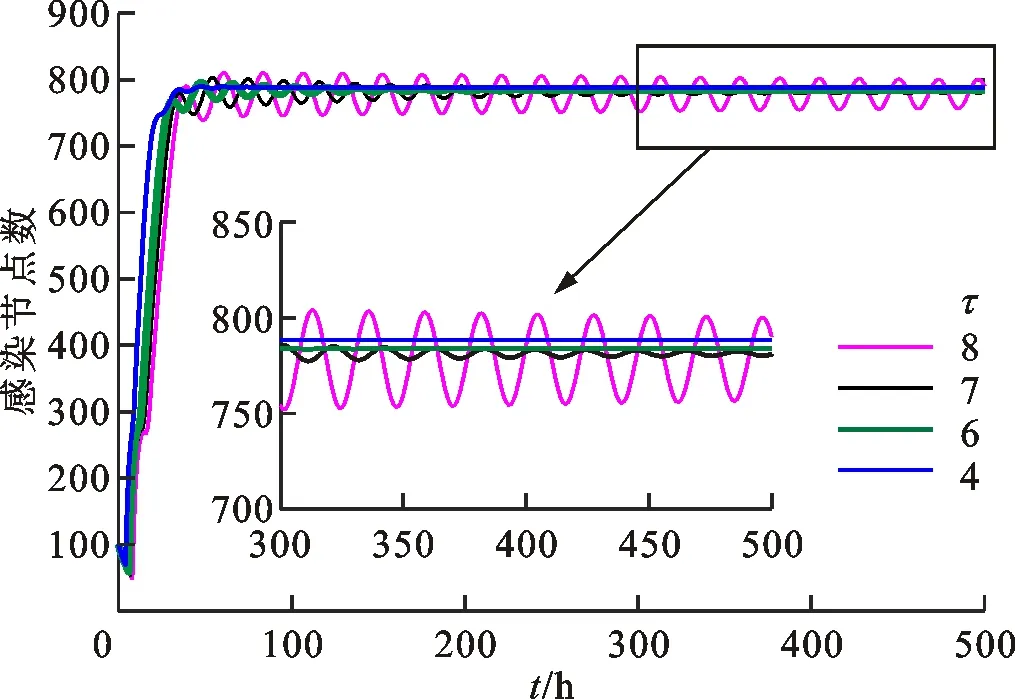
图4 β=0.08时低感染时滞下感染节点数的变化曲线


表1 不同感染时滞下的平均感染节点数
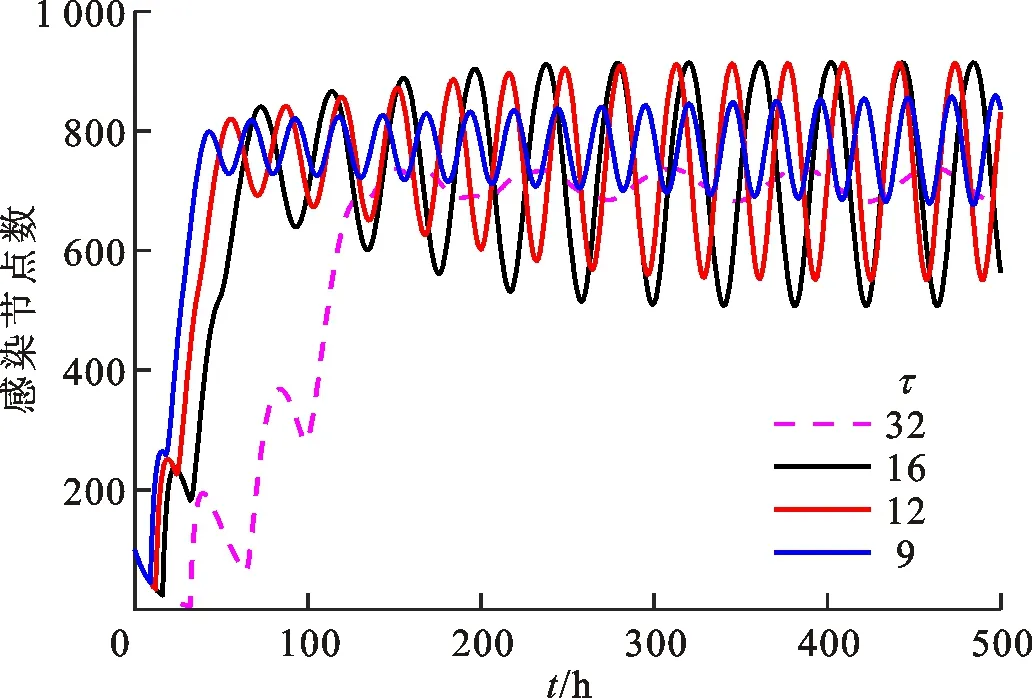
图5 β=0.08时高感染时滞下感染节点数的变化曲线
本小节仿真结果表明,R0和τ0是网络中病毒传播的阈值,感染时滞对网络中病毒传播的影响有2个方面:①感染时滞会影响网络中感染节点的数量,感染时滞表示感染过程耗时,这一过程耗时越长,则被操作系统切换打断的概率越大,相应地感染成功率越低,感染节点数越低;②感染时滞较高时,即使感染率完全相同,平均感染节点数也相差不大,但由于存在振荡现象,无法根据某一时刻的感染节点数判定网络的安全环境,为抑制病毒传播带来困难。
4.2 操作系统切换频率对病毒传播的影响
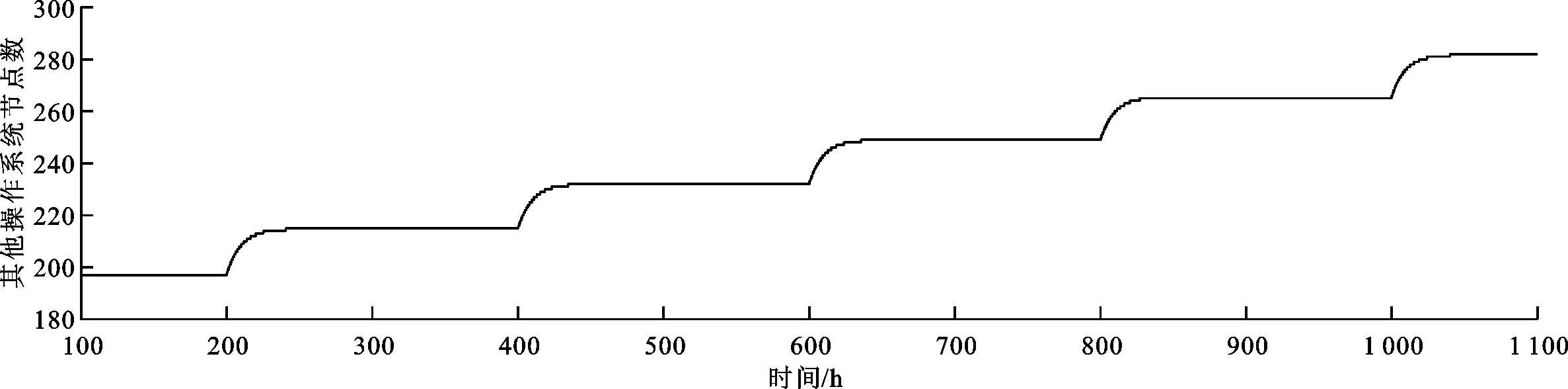
令β=0.08,τ=10。结合定理1、定理2、式(19)(20)计算可得:当dA≤0.012时,感染节点数出现振荡;当0.012 (a)低切换频率 (b)高切换频率图6 τ0<11时感染节点数的变化曲线 由图6a可知,当dA≤0.012时,网络中感染节点数表现出周期性振荡,无法稳定在特定位置。由图6b可知:当0.012 图7 R0<1.1时感染节点数的变化曲线 本小节仿真结果表明:①调整操作系统切换频率能够改变感染时滞的阈值τ0,当节点数存在振荡时,可调节操作系统切换频率增大τ0,使网络达到稳定状态,有利于对网络安全环境的判定;②调整操作系统切换频率能改变平衡点的位置,当病毒持续存在时,可增大操作系统切换频率,使网络平衡点从有病毒平衡点移动至无病毒平衡点,直至消除病毒。 根据感染节点在网络中的规模,可粗略估计相关参数,进而对网络进行相对精准的调整。对于存在感染时滞的操作系统病毒,根据理论分析和数值仿真可知,当τ>τ0时,感染节点数会发生振荡,不利于抑制操作系统病毒传播。取β=0.08,τ=10,此时R0=4.107 6>1,τ0=8.459 8<τ,仿真验证所提策略对病毒的抑制效果。未采取任何措施时,网络中病毒传播情况如图8所示,可以看出,操作系统病毒在网络中能够持续存在,且存在振荡现象。 图8 实施抑制策略前病毒传播情况 考虑振荡对网络安全环境评估的负面影响,首先尝试消除网络中的振荡现象。按照所提策略,在当R0>1,τ>τ0时,可首先对参数dA进行微调,当振荡消除后再根据式(20)进一步调整。设ΔT=200,m=0.001,ΔI=1%,按照本文策略对参数dA进行调整。dA的变化如图9所示,τ0随dA的变化如图10所示,抑制策略执行过程中病毒传播情况如图11所示。 图9 本文策略下dA的变化曲线 图10 本文策略下τ0随dA的变化曲线 (a)网络节点数变化 (b)[100,1100] h时间段内其他操作系统节点数变化图11 本文策略下网络节点数的变化曲线 由图10可知,初始状态下,时滞阈值低于当前时滞,网络中节点数出现如图11a所示的周期性振荡,且振荡幅度大于设定的阈值。为消除振荡,进行了图9中[200,1 200] h时间段所示的操作系统迁移频率的小幅度提升,使相应时间段内振荡幅度逐渐减小,如图11a所示,并且使其他操作系统节点呈阶梯变化,如图11b所示。3次微调后,操作系统切换频率为0.013,已经满足条件τ<τ0,能够消除网络中感染节点数的振荡。但是,振荡消除的表现为振荡幅度逐渐减小直至消失。因此,在振荡未完全消失且幅度仍大于所设定阈值时,网络依旧判定振荡存在,所以再次进行了两次操作系统切换频率的微调。振荡消除后,由式(20)计算可得,dA≤0.704时网络理论上能够消除病毒。仿真中取dA=0.075。抑制病毒传播过程中,感染节点数变化超过设定的阈值,这一过程中dA存在小幅调整,但随着感染节点的消除再次恢复。 本小节结果表明,感染时滞和节点操作系统的切换影响着网络中病毒传播的稳定性。一方面,感染时滞和操作系统的切换频率影响网络平衡点的取值;另一方面,当网络存在有病毒平衡点时,感染时滞和操作系统切换频率共同影响着时滞阈值,当感染时滞高于这一阈值时会导致网络中S、I和R状态节点数的振荡,影响对当前网络安全态势的感知。因此,在网络中针对性部署平台动态目标防御技术,动态调整网络中不同操作系统之间的切换频率,有利于有效评估网络安全态势,抑制操作系统病毒的传播。 (1)基本再生数是病毒感染能力和网络免疫能力的综合体现,其阈值为1,小于该阈值时,网络能消除病毒,否则病毒持续存在。基本再生数与感染时滞负相关,与操作系统切换频率正相关。 (2)感染时滞的阈值随操作系统切换频率和感染时滞动态变化,且正相关。在基本再生数大于1的情况下,当感染时滞小于该阈值时,网络稳定在特定平衡点附近,当大于该阈值时,网络在平衡点附近周期性振荡。 (3)操作系统病毒防御过程中,感染时滞无法人为调节,可调整操作系统迁移频率消除振荡,抑制操作系统病毒传播。
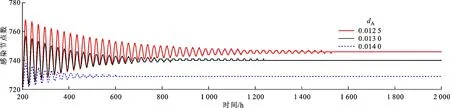

4.3 病毒抑制策略有效性验证



5 结 论
