特殊螺纹接头各向异性试验载荷包络线的计算

陈玉鹏，吕春莉，骆静辉

（天津钢管制造有限公司，天津300301）

0 引言

特殊螺纹接头（premium connection）是在API螺纹接头基础上发展起来的，目的在于克服API 螺纹在性能上的缺陷，它适用于各种复杂应力环境，经验表明特殊螺纹接头在使用中表现出了优异的性能[1-2]。基于ISO 13679 或API 5C5 的接头全尺寸评价试验是评价特殊螺纹接头性能的基本方法，全尺寸试验主要包含三个方面的内容：上卸扣试验、密封试验和极限载荷试验。其中密封试验需要利用Mises 等效应力公式构造试验载荷包络线，用于表征接头的极限性能并计算试验需要的载荷。

随着试验标准的不断升级，耐蚀合金油井管的各向异性已经引起了重视，在新版API 5C5 2017 标准中已经提出了相关问题[3]。但标准并未给出明确的计算方法，只是提及如果进行横向拉伸或者压缩试验，试验的最小屈服强度可用于计算接头评价试验载荷包络线。近几十年来，各向异性屈服准则的理论研究得到很大发展，常用的各向异性屈服准则分为三个系列，即Hill 系列、Hosford 系列和Drucker系列，其中Hill48 屈服准则应用最为广泛[4]。

本文以一种超级双相不锈钢管为研究对象，通过力学性能试验，研究了这种高合金材料的各向异性。根据试验数据，利用Hill48 各向异性屈服准则计算了试验载荷包络线。对于具有各向异性的高合金油井管，该计算方法可用于确定特殊螺纹接头全尺寸评价试验的试验载荷。

1 试验内容及方法

1.1 力学性能试验

本文研究了一种125KSI 钢级SAF2507 超级双相不锈钢管，其规格为φ250.83 mm×16.97 mm，通过冷拔工艺加工至成品管尺寸。在管体周向四个象限内分别取四象限轴向拉伸试样和压缩试样，横向拉伸及压缩试样，试样尺寸均为φ6.25 mm 圆棒试样。试样尺寸如图1 所示。在材料万能试验机上进行拉伸及压缩试验。试验过程参照ASTM A370 试验标准要求。其中压缩试验在达到规定总应变量以后，停止加载。将非比例延伸强度Rp0.2作为材料的屈服强度。通过比较此种材料在不同方向上的屈服强度差异来研究材料的各向异性问题。

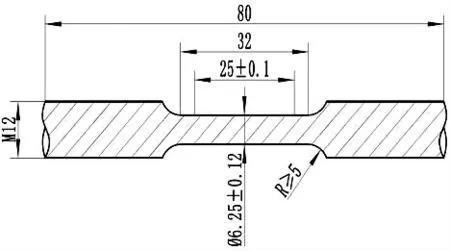
图1 试样尺寸，单位：mm

2.2 HILL 各向异性屈服准则的应用

屈服准则是判定材料中某点的应力分量满足一定关系后产生塑性变形的依据。1948 年，Hill 在Mises 屈服准则基础上，将各向异性引入屈服函数中，提出了Hill1948 各向异性屈服准则，简称Hill48屈服准则[5]。其表达式如下：

其中f（σij）为应力张量函数，F、G、H、L、M、N为描述各向异性的常数。σx、σy、σz、τyz、τzx、τxy为9 个应力分量。当F=G=H=1，L=M=N=3 时，HILL48 屈服准则与Mises 屈服准则的表达式完全相同。

对于管材而言，因所研究载荷只涉及轴向载荷及压力，故只考虑正交方向三个主应力，各向异性的主方向分别位于轴向x、环向y及径向z，综上可得出屈服准则的表达式为：

式中：σa为轴向应力；σh为环向应力；σr为径向应力。

如果X，Y，Z分别表示各向异性主方向上的屈服强度，则HILL 各向异性常数与各个方向上的屈服强度的关系为：

在基于Mises 屈服准则的试验载荷包络线中，试验载荷被分成四种组合形式，分别位于十字坐标轴的四个象限内：第一象限包含拉伸+内压，第二象限包含压缩+内压，第三象限包含压缩+外压，第四象限包含拉伸+外压。Hill 各向屈服准则考虑了三个方向上的各向异性，但并不区分拉伸和压缩。如果将四个象限分别应用Hill 公式，可计算出相似形式的试验载荷包络线。如前文所述，由于径向应力并不能通过试验直接得到，这里可进行简化处理，第一，在径向上不会产生拉应力，即在内压和外压作用下，在径向上永远是压应力。第二，根据相关经验及数据显示，径向压缩屈服强度可视作与轴向拉伸屈服强度相等。则只要分别计算出每个象限的各向异性常数F、G、H，最后将Lamè 公式及轴向应力带入Hill 屈服准则表达式（不考虑弯曲应力），即可计算出每个象限的压力与轴向载荷的关系函数表达式。

轴向应力公式：σa=Fa/AP

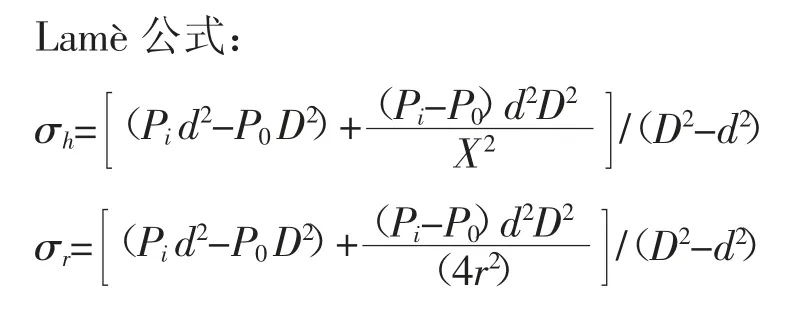
其中：Fa：轴向载荷；Ap：管体横截面积；D：管子外径；d：管子内径，d=D-2t；t：管子壁厚；Pi：内压；P0：外压；r：径向坐标，（d/2）≤r≤（D/2）。

2 试验结果及讨论

2.1 拉伸及压缩试验

纵向和横向拉伸压缩力学性能试验结果表明，冷加工的SAF2507 超级双相不锈钢具有明显的各向异性。表1 为拉伸及压缩试验数据表。图2 比较了材料在不同试验中的平均屈服强度。其中横向压缩屈服强度最高，达到1 006 MPa，纵向压缩屈服强度最低仅有852 MPa，相差154 Mpa；纵向拉伸和压缩屈服强度也存在较大差异，两者相差137 MPa。在进行试验载荷计算时，如果仍按照传统的试验载荷计算方法，即将材料压缩屈服强度等同于拉伸屈服强度，那么会造成接头在轴向压缩载荷下发生失稳的可能性变大。

表1 拉伸/压缩试验数据

图2 SAF2507 超级双向钢平均屈服强度对比

2.2 各向异性试验载荷包络线的计算

根据力学性能试验结果，选择每个方向上的最小屈服强度，使用管体名义外径及壁厚，计算了各向异性材料管体试验载荷包络线（特殊扣接头全尺寸评价试验载荷包络线通常根据管体确定，即假设接头的性能与管体等同）。图3 为各向异性接头名义试验载荷包络线与各向同性接头名义试验载荷包络线对比图。名义试验载荷包络线即为100%效率。表2 为两种计算公式根据ISO13679 A 系试验载荷点计算的具体数值，其中轴向载荷及内压基于95%载荷包络线，外压基于API 挤毁压力。

图3 各向异性接头试验载荷包络线对比图

2.3 各向异性试验载荷包络线的分析

从图3 的对比图中可以看出，利用Hill48 各向异性屈服准则计算的接头试验载荷包络线充分体现了材料在纵向和横向、拉伸及压缩中表现出的性能，客观的表现出材料的各向异性差异。如第一象限中，材料受到轴向拉伸载荷及内压载荷，内压在管子上产生环向拉应力及径向应力，由于材料实测横向拉伸屈服强度小于纵向拉伸屈服，而横向拉伸屈服强度对应环向拉应力，则反映在曲线上为Hill公式计算的内压载荷小于基于各向同性的Mises 公式计算的内压值。又如第三象限，材料受压缩载荷及外压载荷，外压在管子上产生环向压应力及径向应力，根据实际的力学性能测试结果，压缩屈服强度小于拉伸屈服强度，则反映在图中为Hill 公式计算的材料的极限压缩载荷与实测值相等，并且小于各向同性的压缩载荷。横向压缩屈服强度对应外压产生的环向压应力，而实测的试验结果为横向压缩屈服强度最高，计算出的外压值也更大。第二、四象限的计算结果类似。

需要注意的是在纵坐标上，第一、二象限交界处，当轴向载荷为零时，内压处曲线出现了不连续的情况，计算内压值分别为117.6 MPa 及120 MPa。原因在于针对径向屈服强度的简化处理，即将径向屈服强度等同于纵向拉伸屈服强度。而在应用Lamè公式时，最大应力通常产生于管子的内表面，即r=d/2 时，此时内压在内表面产生的径向应力为-Pi，而外压在内表面产生的径向应力为0，也就是说径向屈服强度对于外压来讲没有任何影响，所以外压作用时，曲线在第三和第四象限的坐标轴上是相交的，并没有产生不连续的现象。另一方面，在API 5C3 油套管性能计算标准附录A 中已指出，将屈服准则简化为两种特殊情形即分别考虑内压和外压，造成了图形在Pi=P0=0 时，在坐标轴交点处过渡并不是光滑的，原因在于计算环向应力及径向应力时Lamè 公式本身内在的影响。如果不存在材料性能的各向异性，那么Hill 公式计算出的试验载荷包络线与Mises 等效应力公式计算出的包络线是完全重合的。

表2 ISO13679 A 系试验载荷点

综上所述，利用Hill48 屈服准则计算出的各向异性材料接头评价试验载荷包络线，客观的反映出了材料实测力学性能的表现，具有较强的合理性。

3 结论

本文通过力学性能试验，对SAF2507 超级双相不锈钢的各向异性进行了研究，并根据试验数据，计算了基于Hill 各向异性屈服准则的特殊扣接头评价试验包络线。结果显示，利用Hill 公式计算的试验载荷包络线是相对合理的，该曲线能够客观体现实验材料的各向异性差异。因此，该计算方法可应用到高合金油井管特殊扣接头全尺寸评价试验中去，同时对保证试验的安全性具有重要的意义。