不同温度下软煤等温吸附/解吸特性

张遵国，赵 丹，张春华，陈 毅，唐 朝

（1. 辽宁工程技术大学 安全科学与工程学院，辽宁 葫芦岛 125105； 2. 辽宁工程技术大学 矿山热动力灾害与防治教育部重点实验室，辽宁 葫芦岛 125105）

0 引言

据统计，中国煤矿开采正逐渐向深部转移，全国开采深度超过1 000 m的矿井已达到47对，少量矿井最大采深已超过1 500 m[1].随着开采深度的不断加深，地层中温度、压力也会逐渐增加.

已有研究表明，温度对煤吸附特性有重要影响.刘彦伟[2]等通过实验研究不同煤阶含瓦斯煤粒的扩散通量与温度的量化关系，结果表明温度升高会诱发吸附瓦斯大量解吸.钟玲文[3]等考虑温度和压力综合作用，认为低温低压区压力对吸附能力的影响大于温度，高温高压区则相反，同时发现吸附常数与温度的变化无明显关系.但在其他学者的研究中，吸附常数均随温度的变化而变化，只是变化规律不相同[4-5].

为定量分析煤的吸附特征，众多研究者分别从动力学理论、热力学理论和位能理论等方面提出了不同的吸附模型[6-9].其中，固体表面单分子吸附理论Langmuir方程应用最多[10].但在现有理论模型中，通常只考虑压力对吸附的影响，而对于温度的影响，多侧重于实验规律及机理分析，温度、压力综合影响下的吸附量计算模型还需进一步研究.

此外，现有相关研究普遍采用煤粉颗粒为研究对象，但块煤与粉煤的对比实验所得吸附结果并不相同[11]，采用能够还原煤体中的原始结构的块煤（通常指原煤）进行吸附/解吸特性实验研究，结果将更接近现场实测数据[12].由于软分层煤（以下简称“软煤”）因强度极低无法加工成原煤试件，且型煤能较好地反映软煤的物理性质[13]，因此型煤已被应用于煤的吸附特性实验研究[13-14].

基于上述分析，本文采用重庆大学与中煤科工集团重庆研究院有限公司联合研制的煤层瓦斯吸附解吸变形动态测试装置[12,15]，以具有强突出危险性的软煤为研究对象，开展不同温度条件下等温吸附/解吸实验，分析温度对煤等温吸附/解吸特征的影响，建立考虑温度、压力综合影响的吸附/解吸计算模型.研究成果对深刻认识煤的吸附/解吸特性具有一定理论意义，并对煤矿瓦斯储量评价（煤层气资源评价）和瓦斯灾害防治具有一定工程指导意义.

1 实验方案

1.1 实验煤样

实验煤样选用渝阳煤矿具有突出危险性的8#煤层软分层.实验室测得煤样水分1.93%，坚固性系数0.16.煤样经破碎、筛分后，选用粒径为0.18～0.25 mm的煤粒与适量清水混合，放入模具内，施加（50± 0.1）kN（约100 MPa）成型力并稳压15 min，制成约Φ25 mm×50 mm的圆柱形煤样.

1.2 实验装置

如图1，采用循环水浴对装置进行恒温，采用GB-3000G型压力变送器配套MPA-010602多功能USB信号采集卡实时采集气体压力数据，并利用计算机按高压容积法原理计算得到不同平衡气体压力下的吸附量，可实现10 °C～70 °C范围内煤样吸附/解吸瓦斯量的测试.其中，压力变送器设高压和低压两个，高压压力变送器用于1.0 MPa以上压力监测，低压压力变送器用于1.0 MPa以下压力监测.

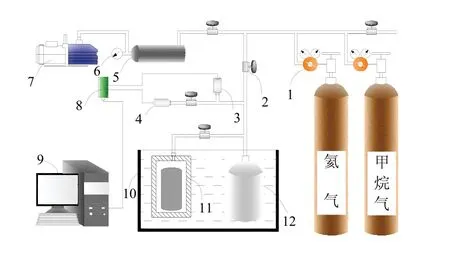
图1 实验装置 Fig.1 experimental device

1.3 实验过程

实验温度分别为303.15 K、313.15 K、323.15 K、333.15 K、343.15 K.实验气体采用体积分数为 99.99 %的甲烷气表征瓦斯.具体实验过程如下.

（1）实验准备.安装煤样，设定实验温度，恒温12 h使煤样温度达到目标温度，并对系统抽真空12 h，将煤样中空气和水分完全排出.

（2）标定自由空间体积.采用体积分数为99.99 %的氦气测定样品罐自由空间体积，排出系统内氦气后再次对系统进行抽真空，确保将系统内及煤样内部残存的氦气全部抽出.

（3）升压吸附.按照加压-平衡-加压过程，逐级提高瓦斯气体压力，使煤样在不同压力下吸附平衡.

（4）降压解吸.待煤样在最高压力条件下吸附平衡后，按照等温吸附试验逆过程，即降压-平衡-降压过程，逐级降低瓦斯气体压力，使煤样在不同压力下解吸平衡.

（5）数据处理 依据实验测得数据，计算得到煤样在不同平衡压力下的吸附/解吸量.

（6）更换煤样 实验结束后，更换煤样，重设目标温度值，进行下一个温度条件下的测试.

2 实验结果

不同温度条件下煤样吸附/解吸实验结果见图2.图2中实线为吸附过程，虚线为解吸过程.

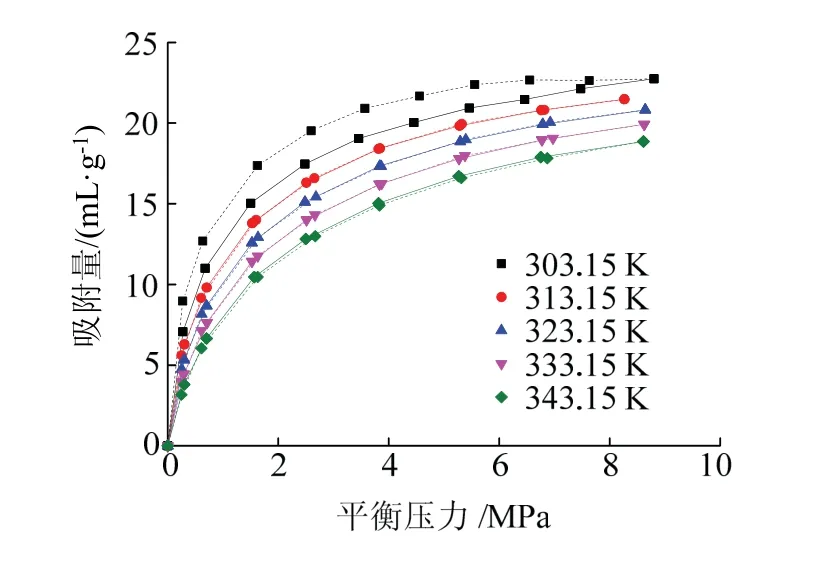
图2 不同温度条件下煤样吸附/解吸量 Fig.2 isothermal adsorption/desorption quantity of coal samples at different temperatures

在理论上，煤吸附甲烷不属于单分子层吸附，但由于甲烷吸附等温曲线符合第I类吸附等温线，所以可以用Langmuir方程[10,16-17]来表示煤的吸附特征.

Langmuir方程为

式中，q为吸附瓦斯量，mL/g；a为饱和吸附瓦斯量，mL/g；b为吸附平衡常数，MPa-1；p为平衡压力，MPa.

煤对甲烷的吸附属于物理吸附，通常认为吸附过程与解吸过程可逆，因此，解吸特征仍可以采用Langmuir方程来表示[12].为了与吸附过程区分并便于分析，解吸特征为

式中，Q为解吸过程残余吸附量，mL/g；A为饱和解吸量，mL/g；B为解吸平衡常数，MPa-1；p为解吸平衡压力，MPa.

采用式（1）和式（2）分别对各煤样吸附/解吸数据进行拟合，得到各煤样等温吸附/解吸常数，R2为拟合精度，见表1.

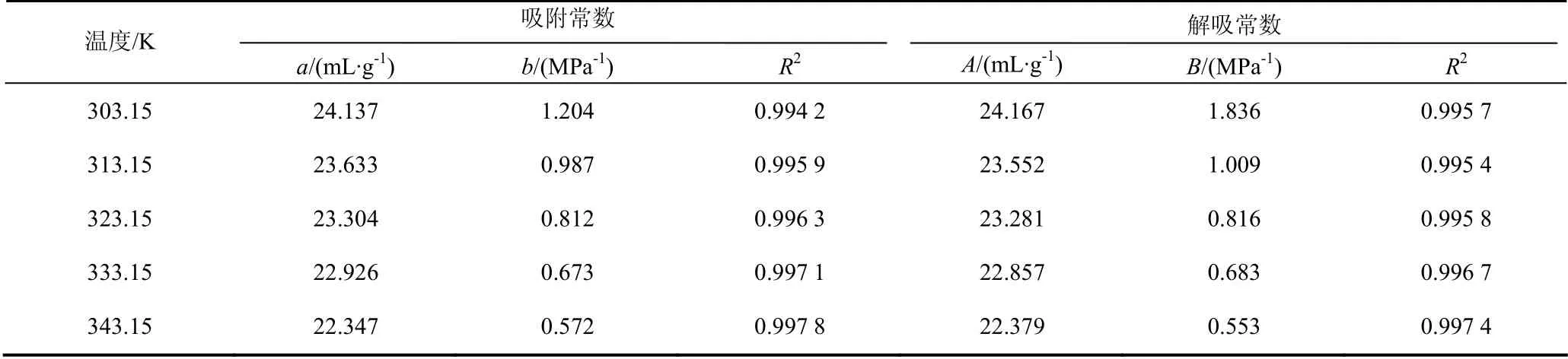
表1 煤吸附/解吸常数 Tab.1 adsorption/desorption constants of coal

3 综合影响下的吸附/解吸模型

3.1 温度对软煤吸附/解吸常数影响

由表1可得到煤样吸附/解吸常数与温度的关系，见图3，图中实线为拟合趋势线.

如图3，吸附/解吸常数均随温度的升高而减小.这是由于煤吸附/解吸本身就是一个动态平衡的过程，温度增加减小了煤体表面自由能，同时温度增加导致甲烷分子活性增强，使煤体捕获甲烷分子的难度增加[18]，导致煤基质束缚甲烷的有效比表面积减小[19]，最终表现为饱和吸附量a随温度的升高而减小；由于吸附/解吸过程可逆，饱和解吸量A也随温度的升高而减小.同时，升高温度可以使甲烷分子获得的能量增加，导致吸附相甲烷分子可以摆脱物理吸附力的束缚而进入游离相中，因此吸附/解吸达到平衡所需压力也就越大，即吸附常数b和解吸常数B均随温度的升高而不断减小.

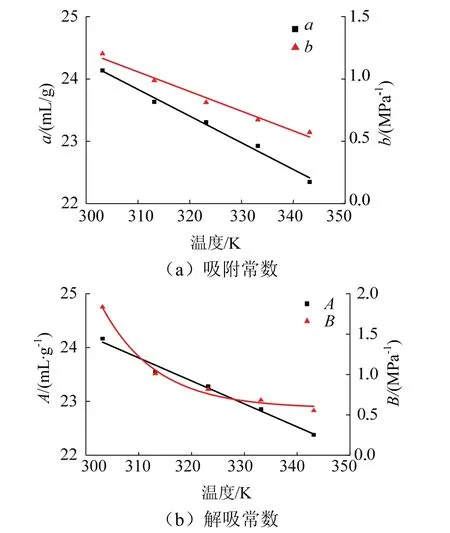
图3 吸附/解吸常数与温度关系 Fig.3 relationships between adsorption/desorption constants and temperatures

根据图3中各常数与温度关系特征，采用一次函数、二次函数、指数函数等多种常用函数关系式拟合相关数据，根据拟合优度R2选取吸附/解吸常数与温度的最佳关系式，见表2.

表2 煤样吸附/解吸常数与温度关系拟合结果 Tab.2 fitting results of relationship between adsorption/desorption constants and the temperature

由表2可知，煤样吸附常数a、b与温度T均呈较好的线性关系，分别表示为

式中，ka和kb为拟合系数，mL/(g·K)，ka反应吸附常数a随温度T变化的快慢，kb反应吸附常数b随温度T变化的快慢；a0为煤样在0 K时饱和吸附量，mL/g；b0为煤样在0 K时吸附速率，MPa-1.

解吸常数A与温度T呈较好的线性关系，而B与温度T呈指数函数关系，分别表示为

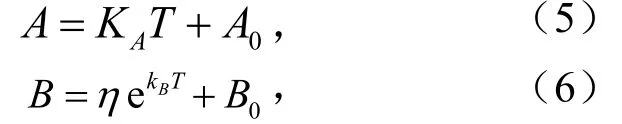
式中，KA和KB为拟合系数，mL/(g·K)，KA反应解吸常数A随温度T变化的快慢，KB反应解吸常数B随温度T变化的快慢；A0为煤样在0 K时饱和解吸量，mL/g；ηB+B0为煤样在0 K时解吸速率，MPa-1.

3.2 模型建立

根据以上拟合结果，将式（3）、式（4）代入式（1），可得到综合考虑温度和压力影响的吸附模型为

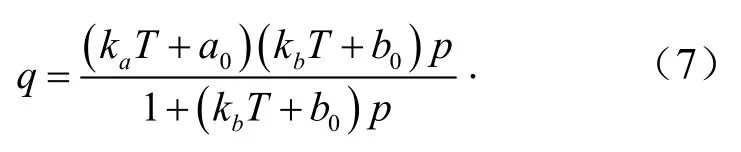
同理，将式（5）、式（6）代入式（2）可得到综合考虑温度和压力影响的解吸模型为

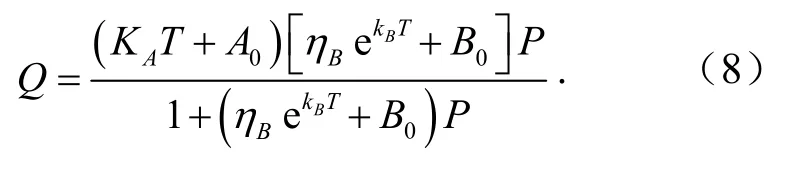
3.3 模型验证

式（7）和式（8）的计算结果和实验结果见图4，图中曲线为模型计算结果，能直观反映温度和压力对煤吸附/解吸特征的综合影响.

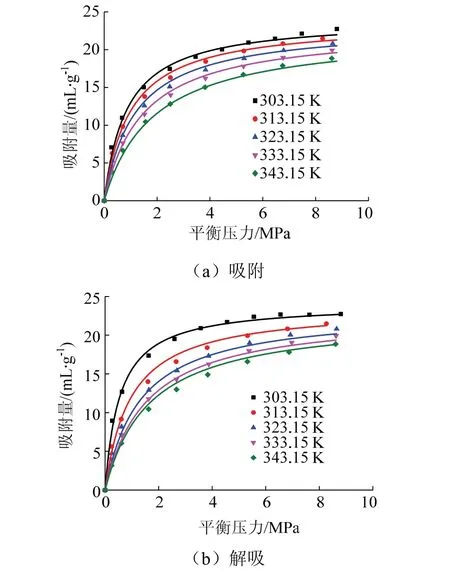
图4 等温吸附/解吸特征 Fig.4 isothermal adsorption/desorption property

为进一步定量评价计算模型的精确性，基于统计学理论，参照拟合相关系数计算式，定义准确度描述模型计算的准确性.假设相同平衡压力下，实验所得吸附量为Qi，通过模型计算所得吸附量为qi，模型准确度为

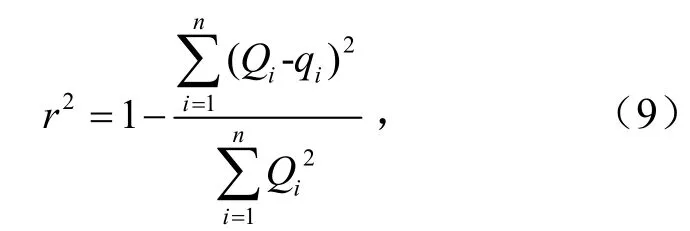
残差平方和是为了直接解释由变量和随机误差产生的影响.统计上将数据点与其回归线上相应的数据之间的差值称为残差，将所有残差的平方值相加，为残差平方和，其值越小，表明数据的拟合程度越好.本文残差定义为实测值与模型曲线上对应数据的差值，残差平方和越小，模型计算越准确.r2介于0至1之间，其数值越大表明模型计算的准确性越高.

利用式（9）计算得到吸附模型式（7）和解吸模型式（8）计算结果的准确度，见表3.

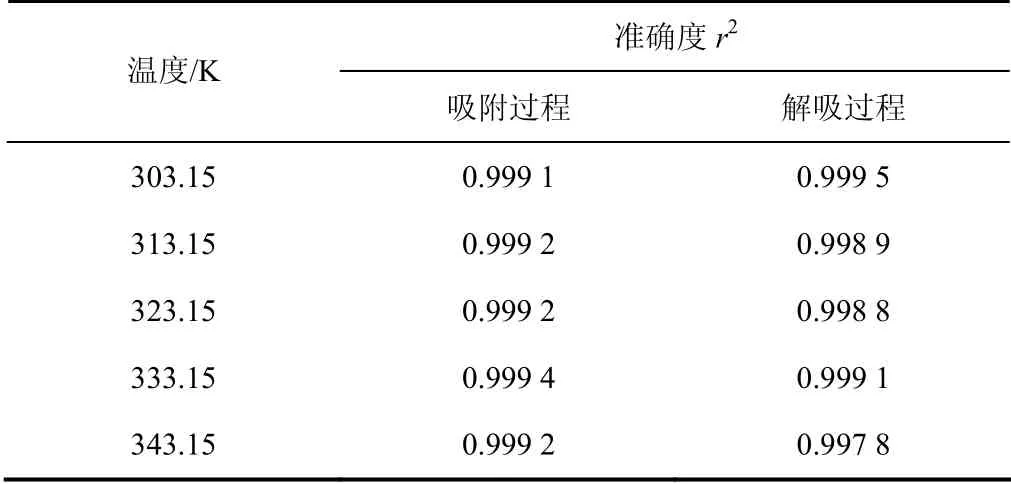
表3 不同温度条件下的模型准确度r2 Tab.3 model accuracy r2 at different temperatures

由图4及表3可知，采用式（7）、式（8）计算得出的吸附/解吸量与实验结果较为吻合，且模型准确度r2均大于0.997.

4 讨论

4.1 常规瓦斯含量预测方法误差分析

目前大多数吸附/解吸实验都是在恒温条件下进行，实验温度通常为303.15 K（摄氏温度30 ℃），即本文最低实验温度.采用式（10）相对误差计算公式，得到其他实验温度下测得的吸附/解吸量与303.15 K条件下Langmuir方程计算所得相同压力下的吸附/解吸量之间的相对误差，见图5.

式中，标准值为313.15 K、323.15 K、333.15 K、343.15 K下吸附/解吸量实测值，mL/g；预测值为采用303.15 K下测得的吸附/解吸特征方程在相同压力下的计算值，mL/g.

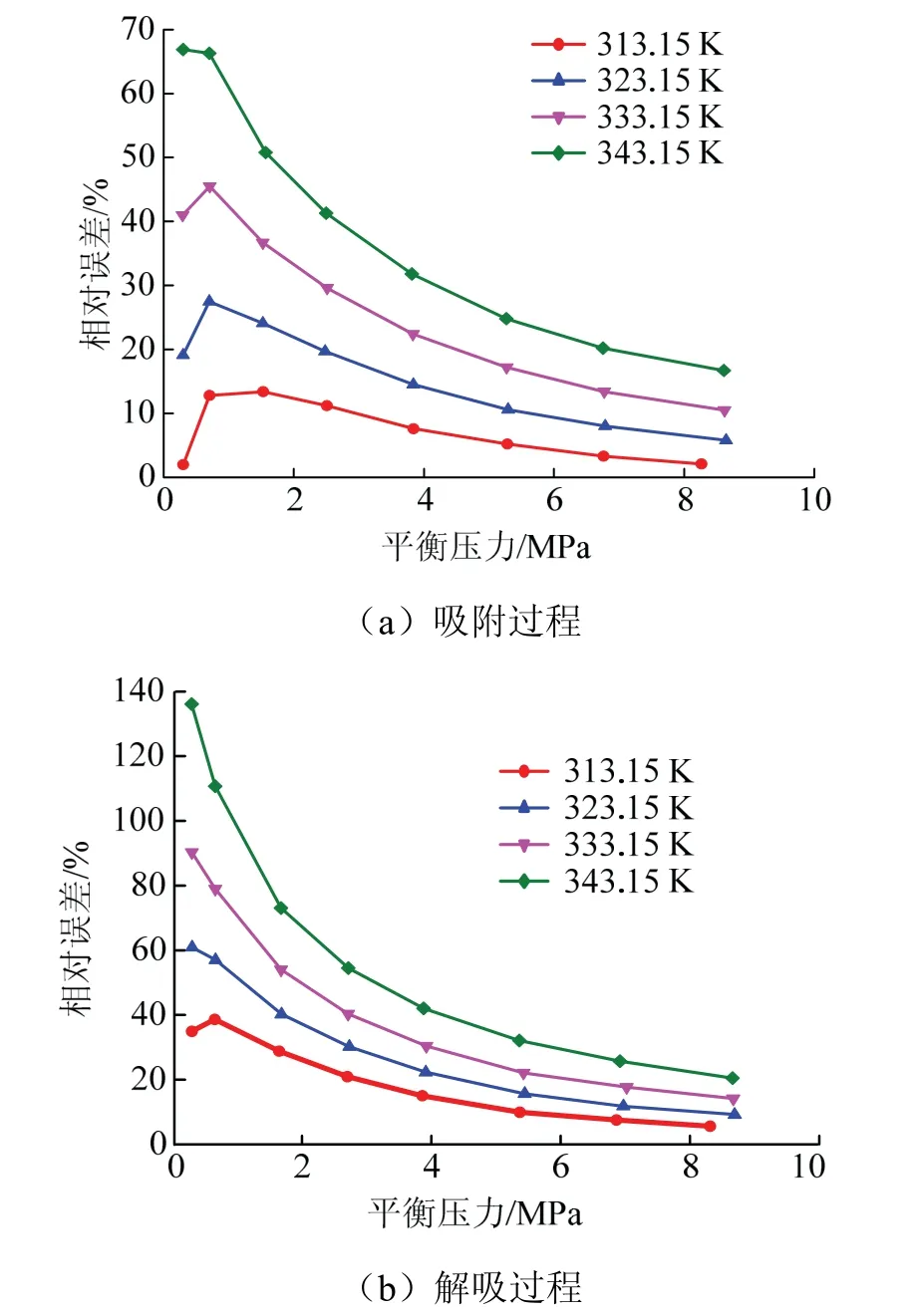
图5 303.15 K条件下等温吸附/解吸曲线计算结果与 其他温度实测结果相对误差 Fig.5 calculated results of isotherm adsorption / desorption curve at 303.15 K are relatively different from the measured results at other temperatures

如图5，无论是吸附过程还是解吸过程，相对误差均随温度的升高而增大，且解吸过程相对误差较吸附过程相对误差更大，吸附过程相对误差最大为 66.9 %，解吸过程相对误差最大为136.1 %.

见图5，不同温度下的相对误差随平衡压力变化趋势略有差异.吸附过程中，313.15～333.15 K下，随平衡压力的增大，相对误差呈现先增大后减小的趋势，且减小速率随平衡压力的增大逐渐减小；343.15 K下，随平衡压力的增大，相对误差始终呈减小趋势，且减小速率也逐渐减小.对比而言，解吸过程中，仅313.15 K下的相对误差呈现先增大后减小的趋势，其他温度下相对误差均相对误差随平衡压力的增大先增大后减小，且减小速率随平衡压力的增大而减小.

由此可见，相对误差受温度和压力综合影响，在低压条件下温度影响较显著，而在高压条件下温度影响明显减弱.

为进一步分析温度与压力对吸附/解吸的影响规律，将303.15 K下测得的吸附/解吸特征方程，即Langmuir等温吸附/解吸模型式（1）、式（2）及本文建立的吸附/解吸模型式（7）、式（8）代入式（10）中.其中，以303.15 K下Langmuir模型计算结果为预测值，本文所建模型计算结果为标准值，得到相对误差与温度、压力的二元方程，进一步获得吸附/解吸过程相对误差随温度、压力的三维分布见图6.图6中实线mn和实线MN分别是吸附过程和解吸过程相对误差为20%的等值线.相对误差小于20%时可以认为Langmuir模型计算结果较准确[20]，此时，可以直接采用303.15 K下测得的吸附/解吸特征方程预测相应温度、压力综合影响下的吸附/解吸量，不必进行不同温度下的实验.

如图6，当平衡压力小于0.5 MPa、吸附过程温度大于317.2 K（即点m），或解吸过程温度大于 308.1 K（即点M），相对差均大于20%，表明不能用303.15 K下测得的吸附特征方程预测温度超过317.2 K、压力小于0.5 MPa下的吸附量，也不能用303.15 K下测得的解吸特征方程预测温度超过 308.1 K、压力小于0.5 MPa下的残余吸附量；当吸附过程平衡压力高于8.3 MPa（即点n）或解吸过程平衡高于9.3 MPa（即点N）），温度低于343.15 K时，吸附/解吸过程模型计算相对误差均小于20%，此时可以直接采用303.15 K下测得的吸附特征方程预测温度低于343.15 K、压力高于8.3 MPa下的吸附量，也可以用303.15 K条件下测得的解吸特征方程预测低于343.15 K、压力高于9.3 MPa下的残余吸附量.

通过以上分析，由于在等压条件下，升高温度会抑制煤的吸附能力，当矿井实地温度与实验温度存在差异时，计算的瓦斯含量值必然和原地差异较大[3].即便考虑20 %可接受误差范围，采用303.15 K下测得的吸附/解吸特征方程预测其他温度、压力条件下的吸附量这种方法适用范围也极为有限.因此，要科学、合理地预测未知区域尤其是深部煤层瓦斯含量，应同时考虑温度和压力对吸附/解吸能力的影响.

4.2 温度和压力综合吸附/解吸模型应用前景

利用温度和压力综合吸附/解吸模型，根据地温梯度和瓦斯压力梯度，可以预测深部某一压力、温度条件下煤对瓦斯吸附量和残余吸附量，进而可以预测瓦斯储量和瓦斯治理工程后的残余瓦斯含量.

假设通过钻井已获知，某含煤盆地的地温梯度为3 °C/100 m，压力梯度1 MPa /100 m，常温带温度为21 °C.已测得煤层埋藏深度为500 m处煤芯在30 °C、40 °C、50 °C、60 °C、70 °C条件下的等温吸附/解吸实验数据，利用上述温度和压力综合吸附/解吸模型，可绘制出温度和压力综合影响下的吸附/解吸过程瓦斯量分布，见图7.

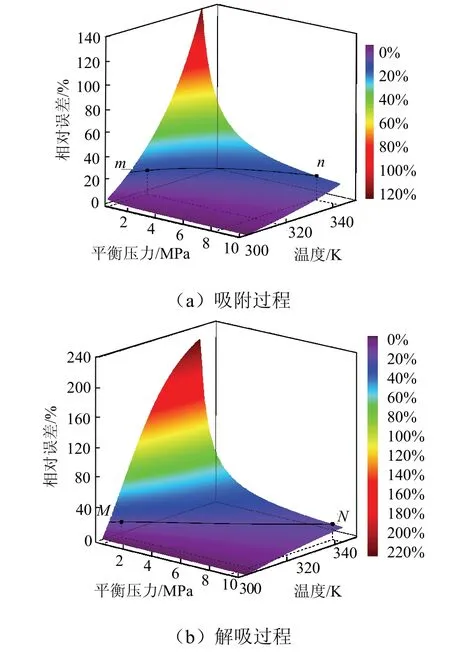
图6 吸附/解吸过程相对误差随温度、压力的变化 Fig.6 relative difference of adsorption / desorption process with temperature and pressure variety

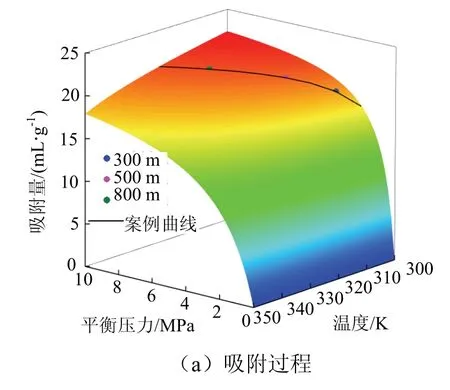
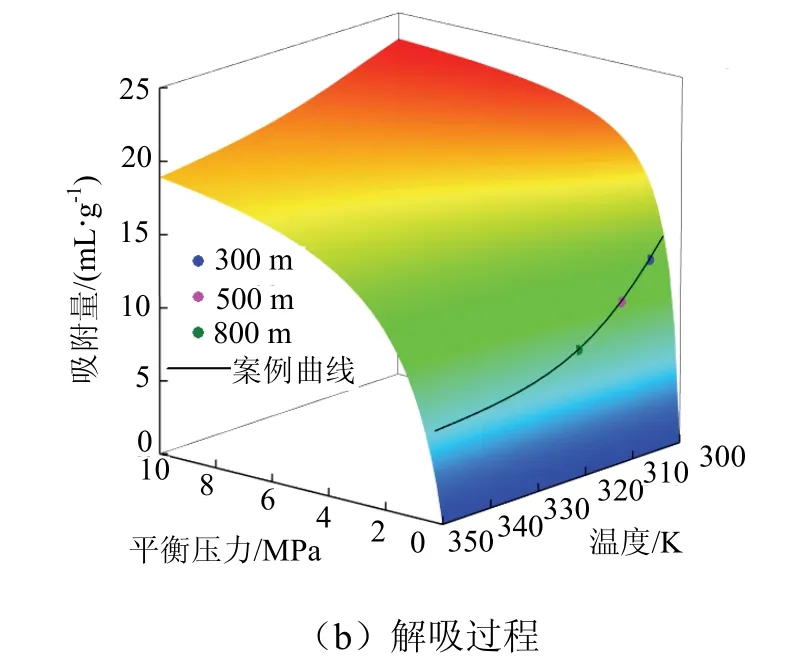
图7 温度、压力综合影响下吸附/解吸量 Fig.7 adsorption / desorption under the comprehensive influence of temperature and pressure

从图7（a）可以看出，埋深300 m处，温度为30 °C、压力为3 MPa时，煤层瓦斯吸附量为 18.760 5 mL / g；埋深500 m处，温度为36 °C、压力为5 MPa时，煤层瓦斯吸附量为20.112 6 mL/g；埋深800 m处，温度为45 °C、压力为8 MPa时，煤层瓦斯吸附量为20.697 9 mL/g.再考虑含气饱和度等参数，可以获得各处煤层瓦斯含量，进一步计算得出煤层瓦斯储量.

当采取瓦斯治理工程后，各处瓦斯压力均降为0.6 MPa，则可以根据图7（b）得出埋深300 m、 500 m、800 m 处残余瓦斯吸附量分别为 12.599 3 mL/g、10.346 1 mL/g、8.059 4 mL/g，再根据相关参数可以进一步计算得出煤层残余瓦斯含量.

5 结论

（1）升高温度会抑制煤的吸附能力.吸附/解吸常数随温度的升高而减小，吸附常数a、b和解吸常数A均与温度呈线性函数关系，解吸常数B与温度呈指数函数关系.

（2）根据等温吸附/解吸常数与温度的函数关系，建立综合考虑温度和压力影响的吸附/解吸模型，利用该模型能够较好地描述软煤在不同温度、压力条件下的吸附/解吸特征，此模型建立方法同样适用于其他煤样.

（3）定义模型计算值与实验值之间关系的准确度r2，其值介于0至1之间，数值越大则模型计算的准确性越高，本文建立的吸附/解吸模型计算结果准确度均大于0.997. （4）以303.15 K下测得的吸附/解吸特征方程用于预测其他温度、压力下的吸附/解吸瓦斯量，预测结果相对误差受温度和压力综合影响，在低压条件下温度影响较显著，在高压条件下温度影响明显减弱.