冒溪煤矿建筑物下急倾斜煤层 充填开采地表变形预测

宋子岭，陈明进,2

（1. 辽宁工程技术大学 矿业学院，辽宁 阜新 123000；2. 越南煤炭矿产工业集团 矿山工艺科学研究院，河内 100803）

0 引言

冒溪煤矿是越南煤炭矿产工业集团在建筑物下、铁路下、水体下（简称“三下”）压煤储量最大的煤矿之一，全矿“三下”压煤储量约30 Mt，其中冒溪煤矿南翼区域“三下”压煤储量约23 Mt.该区域煤层为急倾斜中厚及厚煤层，开采难度大，采用留设保护煤柱法、部分开采法等，效果均不理想，因此，对该区域选择合理的开采方法尤为重要.

充填开采是解决“三下”煤炭资源开采难题的有效方法之一.张王磊[1]采用概率积分法，利用地表下沉预测软件对该矿“三下”采后进行地表变形预测.许家林[2]等揭示覆岩关键层对地表沉陷控制机理，建立基于关键层控制理论的地表沉陷控制模型及部分充填采煤的设计方法.陈元非[3]对充填条带岩层移动及上覆岩层破坏过程进行相似材料模拟，研究充填条带采宽、煤柱宽度、采高、充填率等与地表移动变形的关系.何荣军[4]等以某矿区建筑物下采煤为例，建立模型并分析粉煤灰膏体充填采煤控制地表沉陷效果.牛明冬[5]等建立地表岩移观测站，进行实地高精度观测，绘制沉降曲线，观察铁路变形情况，解决铁路下压煤问题.王家臣[6]等采用相似材料模拟方法研究支架初撑力、工作阻力、充填夯实力、充填率等因素对上覆岩层移动规律的影响.邹徐文[7]提出“宽条带跳采全采垮落带浆体注充控制覆岩移动及地表沉陷”的“三下”压煤开采技术并建立模型，研究不同覆岩结构类型条件下，不同采深和不同采宽煤层开采时垮落带的形成特点及规律.赵学义[8]等运用概率积分法，对全部跨落法和膏体充填开采法的地表变形规律进行预测.卢央泽[9]应用ANSYS软件揭示煤矸石胶结充填法的地表移动规律.孙晓光[10]等用FLAC软件研究在上层煤未采和已采情况下，开采下层煤后的地表沉陷和顶底板弹塑性区分布，分析充填开采时工作面矿压及顶板稳定性.SUN Weibo[11]等通过离散元数值试验，研究了不同条带充填条件对导流裂隙带的影响，得出上向裂隙和下向裂隙贯通是阻水岩群失稳的直接原因.

在越南，煤矿充填开采的研究相对较少，2006年，冒溪煤矿在V8工作面试验充填采煤法，验证充填开采法满足要求并能减小地表沉陷.2012年，越南煤炭矿产工业集团矿山工艺科学研究院进行充填开采控制顶板并保护地表环境的研究，但急倾斜煤层充填开采方法在越南矿区开采中还没应用，没有形成系统的理论和方法.深入研究冒溪煤矿建筑物下急倾斜煤层充填开采方法以及充填开采后围岩移动变形规律，对解决越南急倾斜煤层开采问题、完善充填开采技术体系具有重要的理论意义和实际意义.

1 急倾斜煤层开采地表变形分析

1.1 滑移空间与开采空间换算

急倾斜煤层开采后，在煤层顶板岩层的一定范围内形成楔形破坏区.岩层破坏主要为弯曲变形，引起上覆岩层滑移变形，采空区上部地表形成下沉盆地.为便于计算急倾斜煤层开采所形成的滑移空间参数，可将急倾斜煤层开采形成的岩层滑移空间视为三角形区域.

急倾斜煤层开采的地表变形移动是由岩层滑移空间引起的，因此，地表移动变形量可通过滑移空间参数的计算来获得.将滑移空间视为不等厚的水平开采空间，则滑移空间的参数可用煤层顶板移动角、煤层底板移动角确定，见图1.

图1 滑移空间主要参数 Fig. 1 main parameters of sliding space

图1 中，△ABO1为实际开采空间，△ABO为滑移空间，则

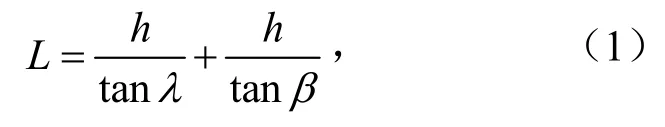
式中，L为边AB长，m；h为实际开采空间的垂直高度，m；λ为底板移动角，°；β为顶板移动角，°；l1为实际开采空间的倾斜长，m；α为煤层倾角，°.

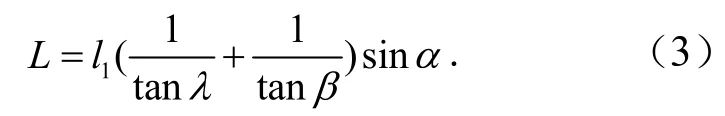
若忽略楔形破坏区内岩层碎胀，则

式中，h′为滑移空间的垂直高度，m；M为煤层的开采厚度，m.

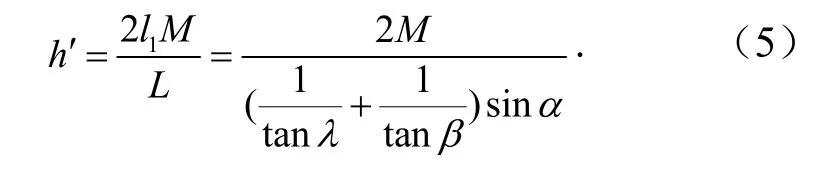
滑移空间是不规则体，所以采用图2所示的剖分法计算地表移动变形，则

式中，Ls为点O'至边BC的距离（O′为滑移空间顶点O在底边AB上投影），m.

图2中的Lz为实际开采空间走向长度，m.

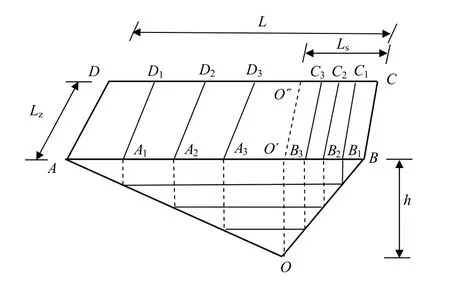
图2 滑移空间的剖分 Fig.2 subdivision of sliding space

将垂直高度h、边OA和边OB沿OO′方向划分为n等份.在区域AO′O″D中平行于AD作n个等间距剖分线A1D1，A2D2，…，AnDn，在区域BO′O″C中平行于BC作n个等间距剖分线B1C1，B2C2，…，BnCn.则可得n个新区域A1B1C1D1，A2B2C2D2，…，AnBnCnDn.

用概率积分法分别计算区域ABCD，A1B1C1D1，A2B2C2D2，…，AnBnCnDn的地表下沉量函数为w0(x,y)，w1(x,y)，w2(x,y)，…，wn(x,y)，叠加后可得急倾斜煤层开采地表下沉盆地为式（7）～式（10）.

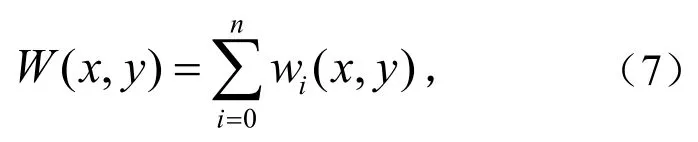
式中， (,)Wxy为地表下沉量，mm.

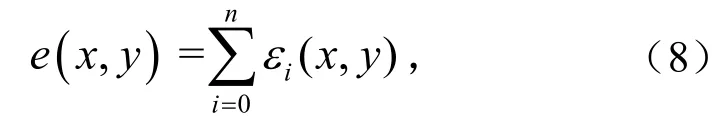
式中，(,)exy为地表水平变形量，mm.

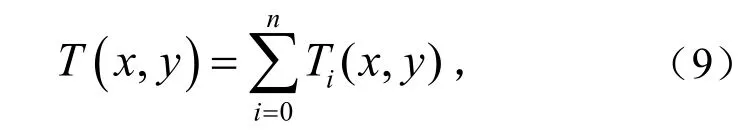
式中， (,)Txy为地表倾斜，mm/m.

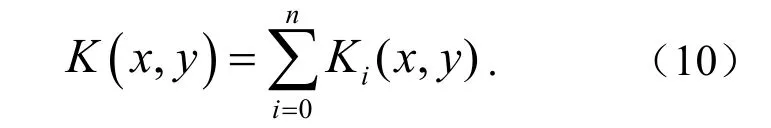
式中， (,)Kxy为地表变形曲率， km-1.

1.2 急倾斜煤层开采地表移动变形量

利用概率积分法的线积分理论，建立地表移动变形量的计算模型如下.

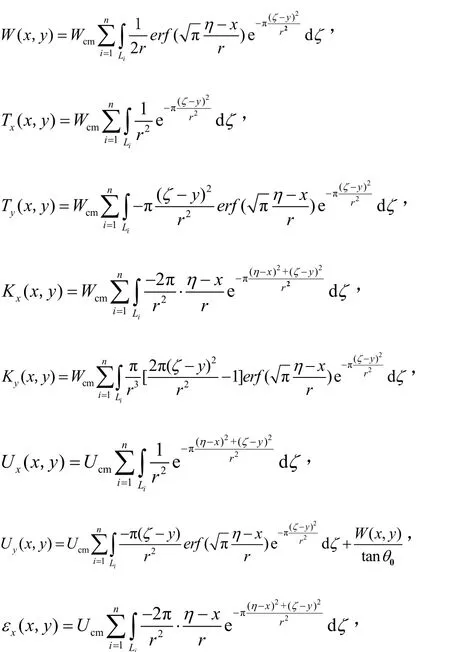
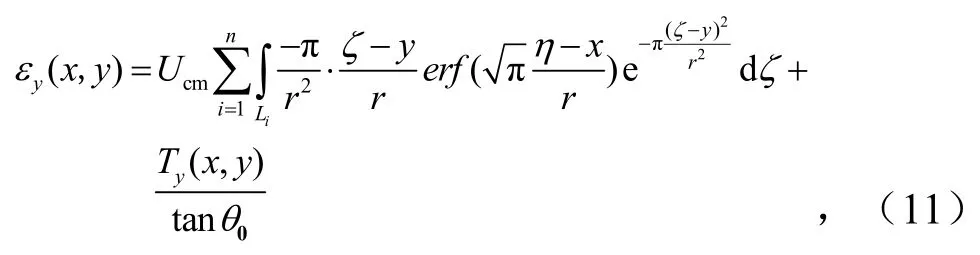
式中，Wcm为充分采动时地表最大下沉值，mm，Wcm=mq·cosα，mm；Ucm为充分采动时走向主断面上地表最大水平移动值，mm，Ucm=bWcm，mm；α为煤层倾角，°；m为开采厚度，mm；q为地表下沉系数；b为地表水平移动系数；H为开采深度，m；r为工作面影响半径，r=H/tanβ，m；β为主要影响角，°；Li为第i个计算工作面的边界直线段AiBi长度，m；θ0为开采影响传播角，°；Tx(x,y)为沿煤层走向的倾斜，mm/m；Ty(x,y)为沿煤层倾向的倾斜，mm/m；Kx(x,y)为沿煤层走向的曲率，10-3km-1；Ky(x,y)为沿煤层倾向的曲率，10-3km-1；Ux(x,y)为沿煤层走向的水平位移，mm；Uy(x,y)为沿煤层倾向的水平位移，mm；εx(x,y)为沿煤层走向的水平应变，mm/m；εy(x,y)为煤层走向的垂直应变，mm/m.

为确定地表移动变形最大值与移动方向，建立移动变形主值计算模型为

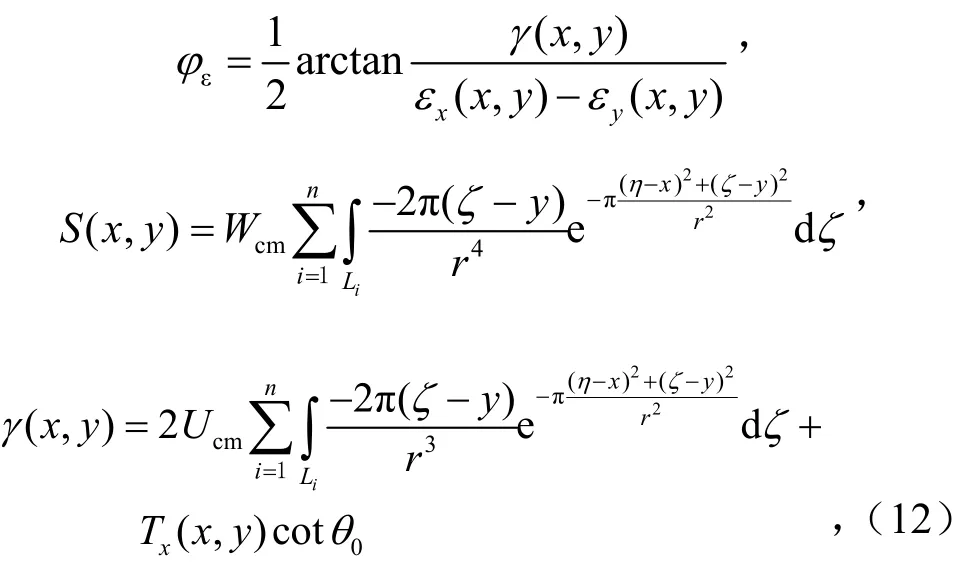
式中，Tm(x,y)为最大倾斜变形量，mm/m；Um(x,y)为最大水平位移，mm；K1,2(x,y)为最大正、负曲率，10-3km-1；ε1,2(x,y)为最大应变值，mm/m；S(x,y)为扭曲变形量，10-3m；γ(x,y)为剪切变形量，mm/m；φi为最大倾斜方向角，°；φu为最大水平移动方向角，°；φk为最大曲率方向角，°；φε为最大拉伸、压缩水平变形方向角，°.

1.3 地表移动变形参数

（1）充分采动条件下，地表下沉系数与岩性的关系见表1.急倾斜煤层开采很难充分开采，因此，实际计算时应对其下沉系数进行折减.

表1 不同岩石的抗压强度和地表下沉系数 Tab.1 compressive strength and surface subsidence coefficient of different rocks

（2）水平移动系数为

式中，Ucm为充分采动条件下走向主断面上地表最大水平移动量，mm；Wcm为最大下沉量，mm；b为水平移动系数.

（3）开采影响传播角为

式中，Uwcm为该点水平移动，mm；θ0主要与煤层倾角α有关，α≤45°时，取θ0=90°-0.68α.

（4）主要影响角正切值为

式中，β为主要影响角，°；rz为主要影响半径，m， rz=l/0.8（l为充分采动时走向主断面上地表下沉值）；Hz为走向主断面上走向边界采深度，m；β值与煤层走向方向主断面边界的采深及主要影响半径有关.根据实测，坚硬岩层，tanβ 取1.2～1.91；中硬岩层，tanβ 取1.92～2.4；软弱岩层，tanβ 取2.41～3.54.

（5）拐点偏距

拐点即充分采动条件下主断面上地表下沉值为0.5Wcm、最大倾斜、曲率为0的3个点值x（或y）的平均值x0（或y0）为拐点坐标.将拐点坐标向煤层投影，投影点到采空区边界的距离为拐点偏距.坚硬岩[12]S=(0.15～0.20)H；中硬岩 S=(0.10～0.15)H；软岩S=(0.05～0.10)H，H为开采深度，m.

2 充填开采地表移动规律

2.1 冒溪煤矿南翼地质条件

冒溪煤矿南翼区域地表相对平坦，标高15～ 70 m.许多地表工程需要保护，例如建筑物（住宅、冒溪煤矿的工业建筑物、工厂、国家供电路线、皮带输送机线路等），铁路（河内-下龙线的铁路和矿区内部铁路），水体（河、大溪、小溪、湖等），此外，矿区内还有旧的露天采场，并已积水.

主要地层是砂砾岩、砂岩、粉岩、较少的黏土岩及砾石岩.地层厚度约1 720 m，其中含有工业价值的煤层共8层，编号分别为V6、V7、V8、V8a、V9、V9a、V9b和V10.

2.2 模型建立与计算方案

FLAC3D软件采用拉格朗日算法和混合-离散分区技术，适用于分析模拟渐进破坏及大变形.采用 FLAC3D的莫尔库仑模块对不同充填率条件下地表移动变形控制作用进行模拟分析.

（1）模型建立

根据冒溪煤矿南翼区域V9b号煤层-80～0 m的地质条件，采用莫尔-库伦模块，建立长×宽×高= 600 m× 600 m×265 m三维模型，划分为302 400个单元、319 850个节点，见图3.煤岩层物理力学指标见表2.

图3 模型的网格剖分 Fig.3 mesh generation of model

（2）计算方案

为研究急倾斜煤层充填开采后地表变形移规律，分别对采空区充填率为0（无充填）、80%、85%、90%时，地表下沉盆地形态和下沉规律进行模拟.

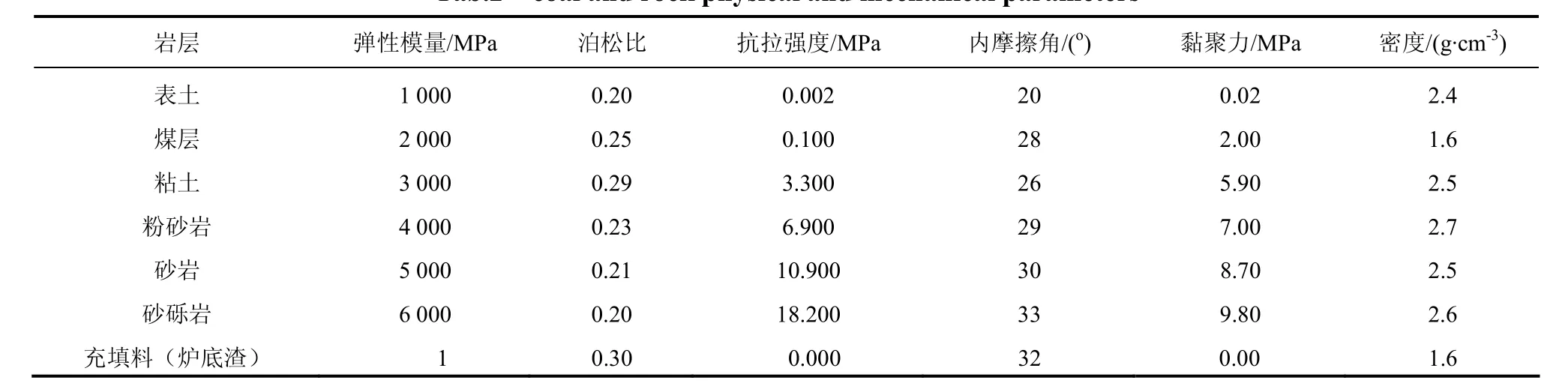
表2 煤岩物理力学指标 Tab.2 coal and rock physical and mechanical parameters

2.3 结果及分析

模拟充填率分别为0、80%、85%、90%时的地表下沉盆地形态和地表下沉.图4为不同充填率的地表下沉盆地形态；不同充填率的地表下沉等值线、地表倾斜及水平变形等值线见图5～图8.

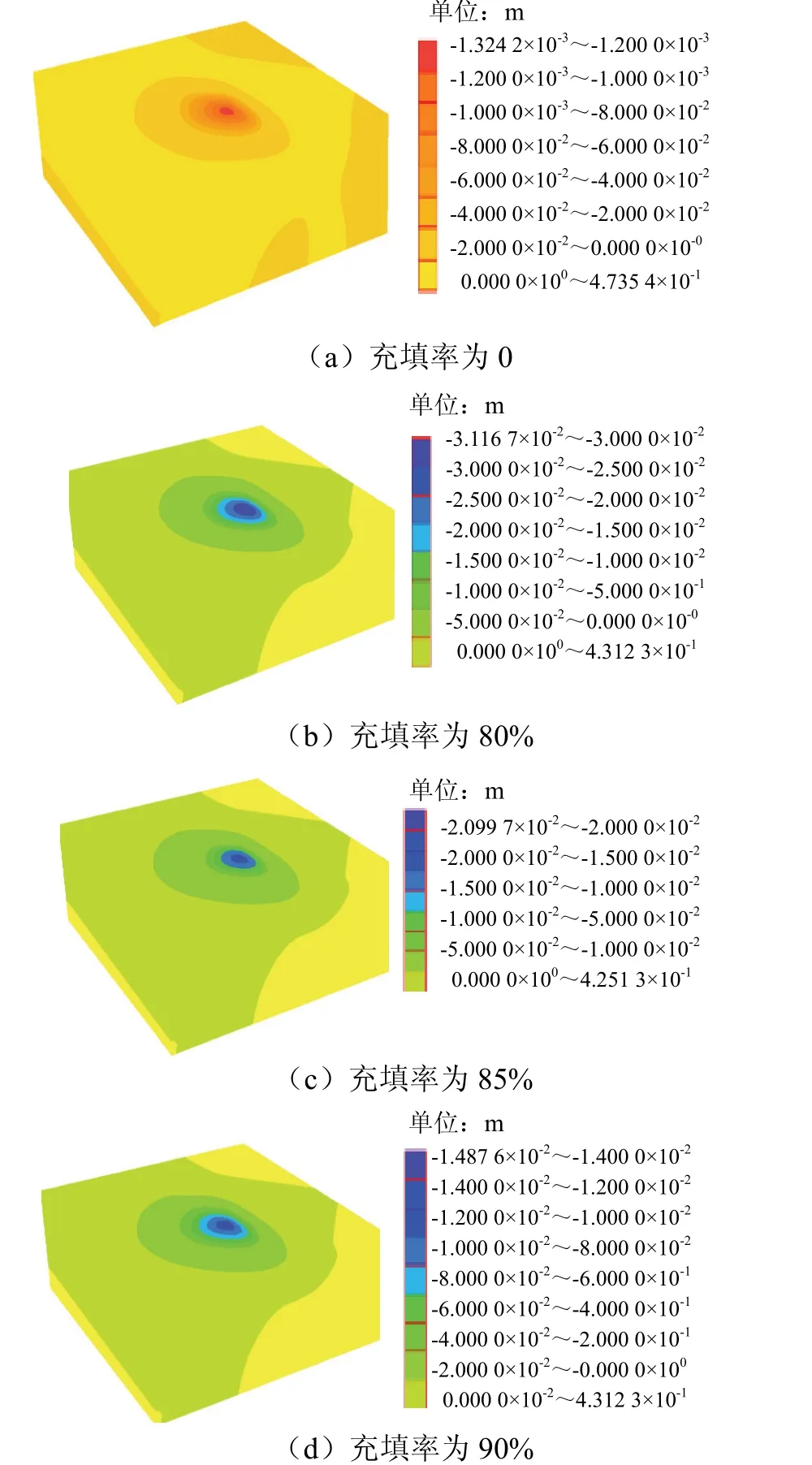
图4 不同充填率条件下地表下沉盆地形态 Fig.4 surface subsidence basin shape under the condition of different filling ratio

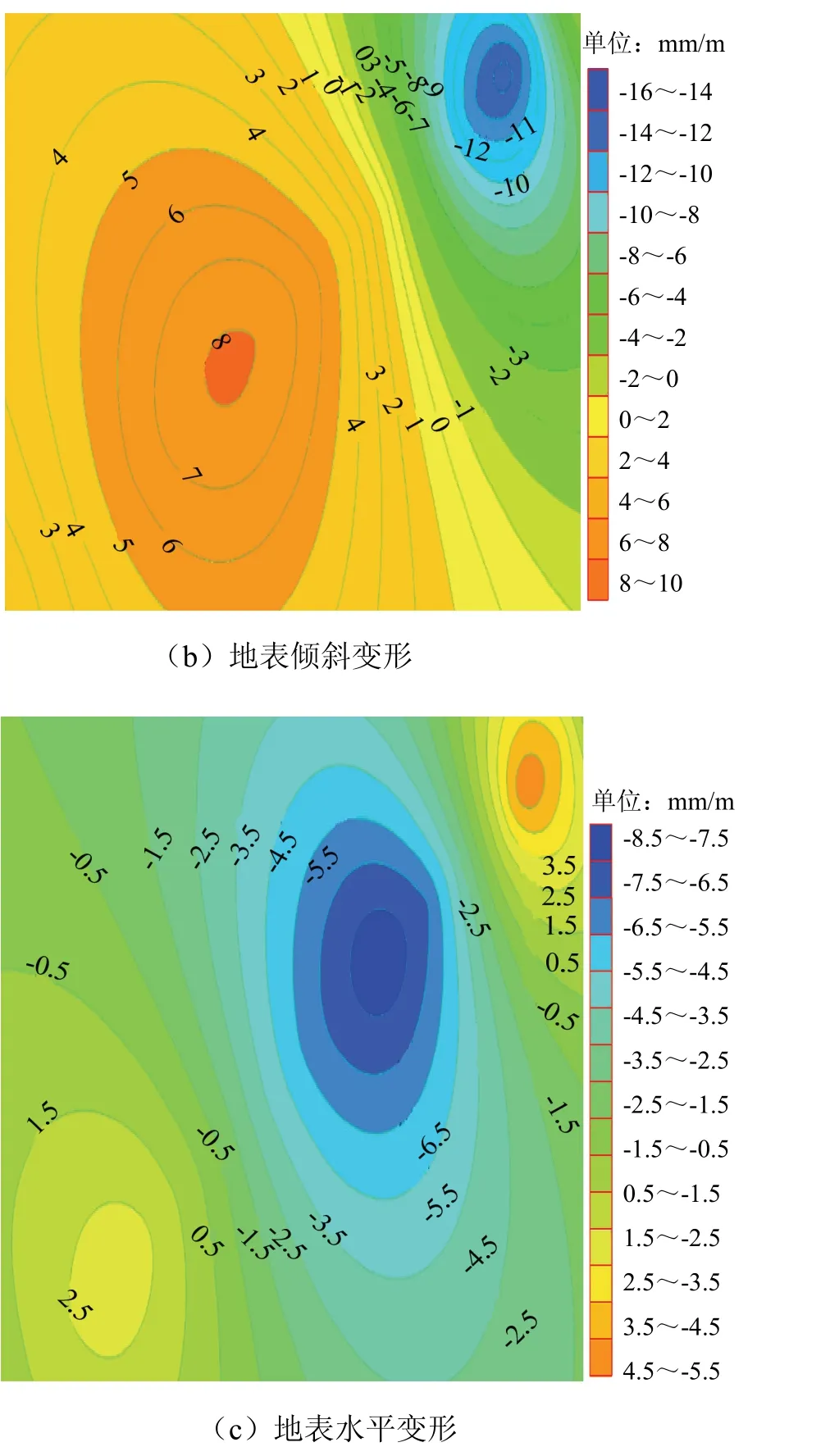
图5 充填率为0时地表下沉、地表倾斜及 水平变形等值线 Fig.5 isoline of surface subsidence, slope and horizontal deformation when filling rate is 0

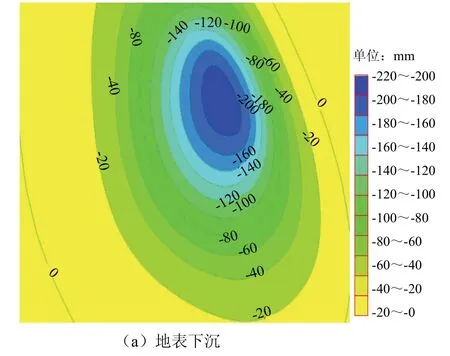
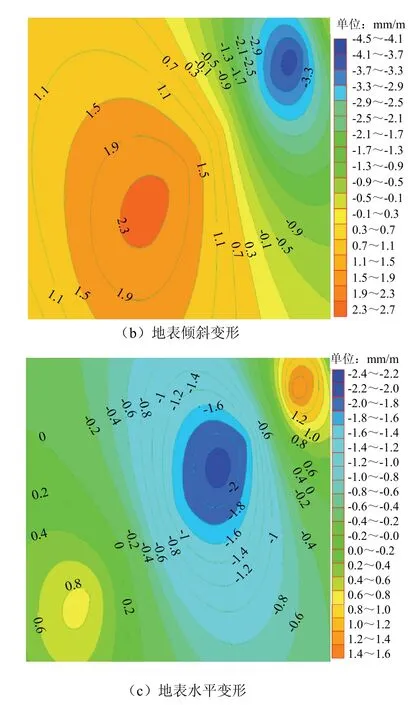
图6 充填率为80%时地表下沉、地表倾斜变形及 水平变形等值线 Fig.6 isoline of surface subsidence, slope and horizontal deformation when filling rate is 80%

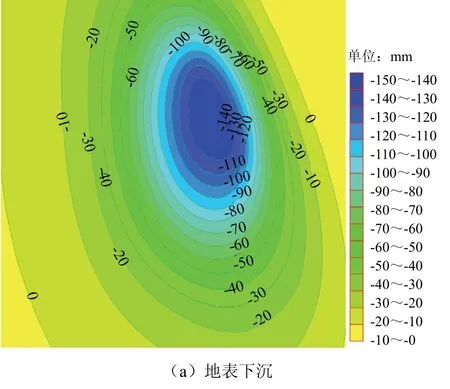
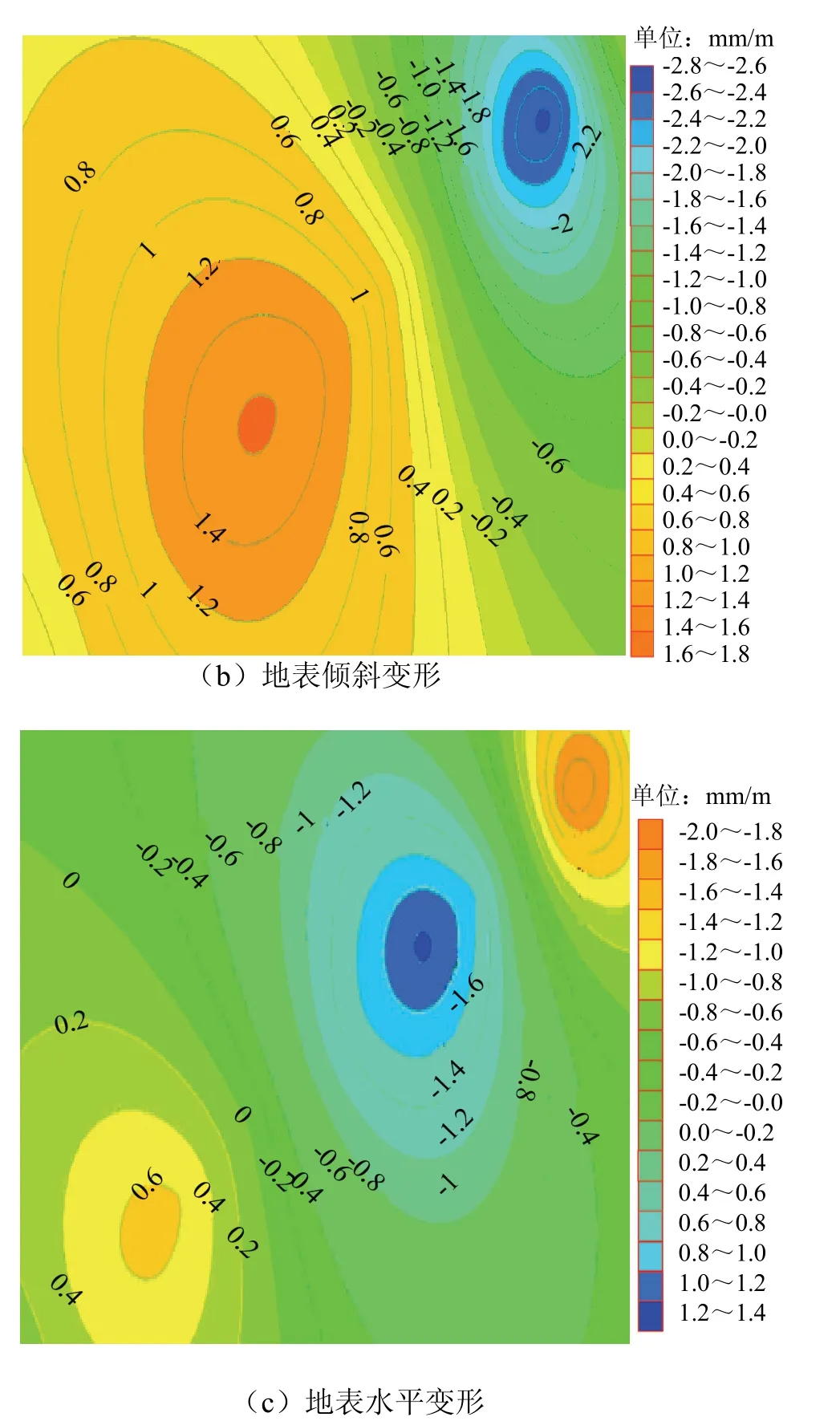
图7 充填率为85%时地表下沉等值线、地表倾斜变形 及水平变形等值线 Fig.7 isoline of surface subsidence, slope and horizontal deformation when filling rate is 85%

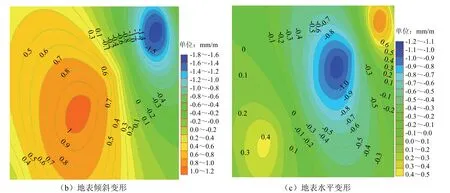
图8 充填率为90%时地表下沉等值线、地表倾斜变形及水平变形等值线 Fig.8 isoline of surface subsidence, slope and horizontal deformation when filling rate is 90%

依据不同充填率对地表移动变形的模拟结果，绘制地表下沉量变化曲线、水平形曲线、地表倾斜变形曲线和地表最大下沉变化曲线，见图9～图12.地表变形的数值模拟结果见表3.

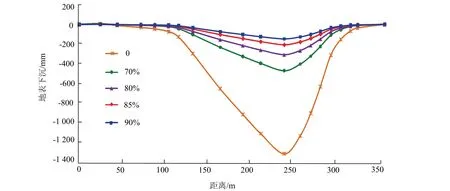
图9 沿煤层走向不同充填率下地表下沉量 Fig.9 surface subsidence value at different filling rates along coal seam strike

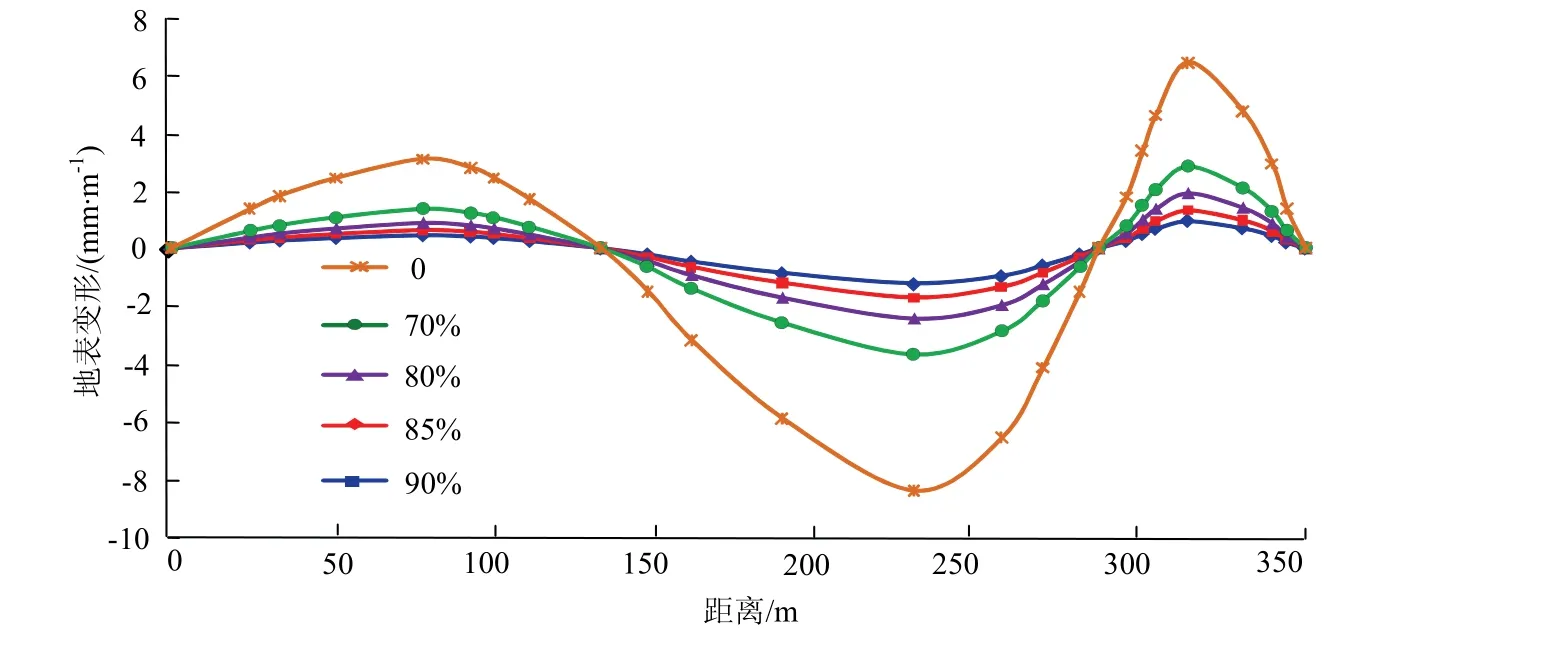
图10 沿煤层走向不同充填率下地表水平 Fig.10 surface horizontal value at different filling rates along coal seam strike

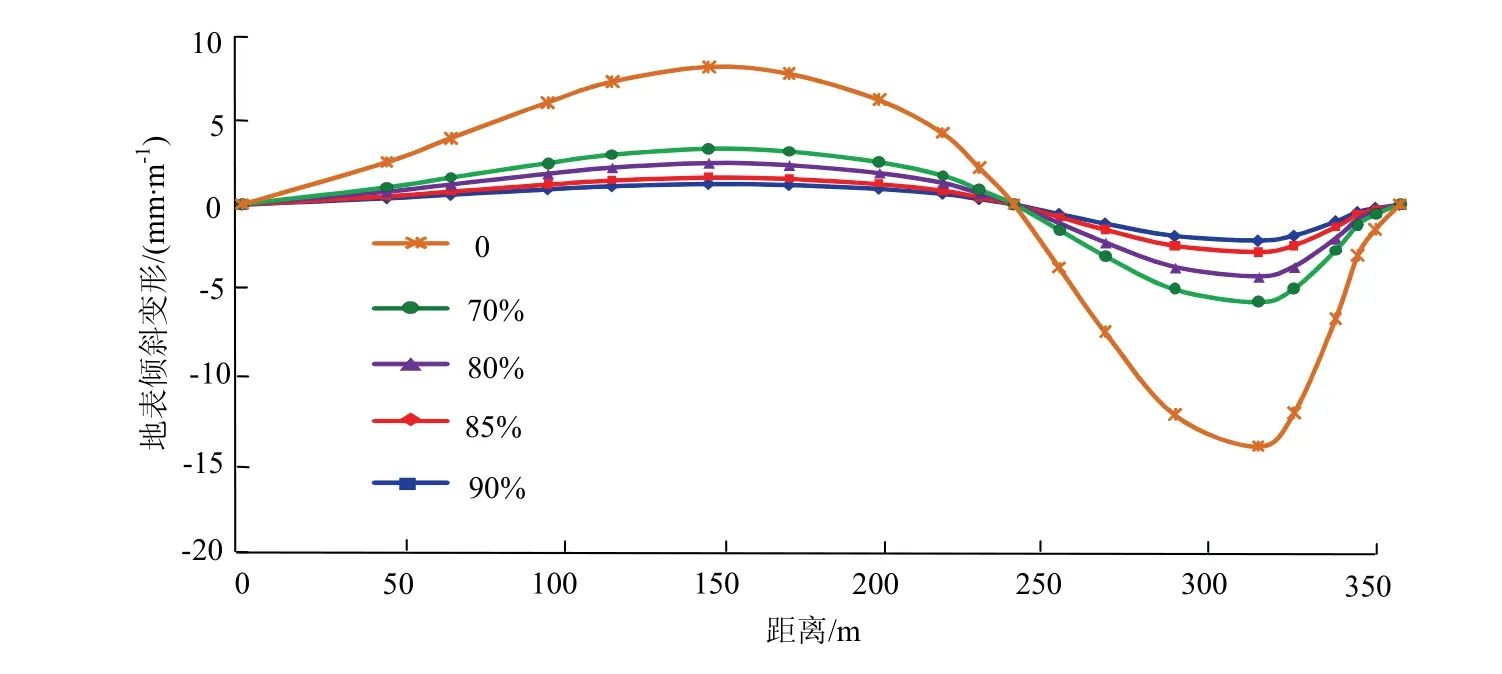
图11 沿煤层走向不同充填率下地表倾斜变形 Fig.11 surface tilt deformation value at different filling rates along coal seam strike

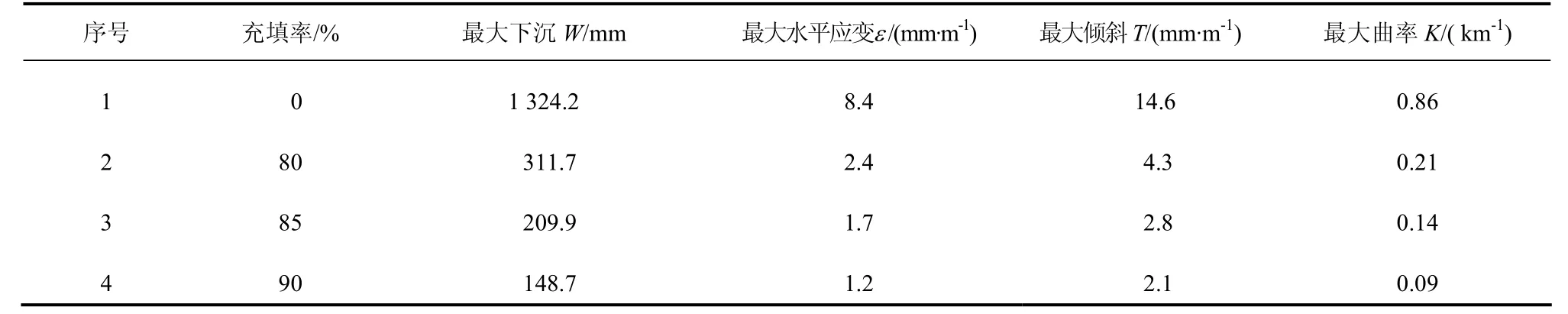
表3 不同充填率时的数值模拟结果 Tab.3 simulation results of different filling rate

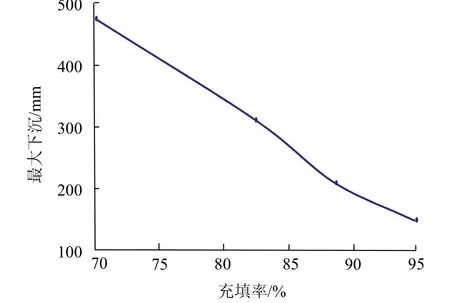
图12 地表最大下沉随充填率变化 Fig.12 relation between largest surface subsidence and filling rate

根据《建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规程》（国家安全监管总局 国家煤矿安监局 国家能源局 国家铁路局2017年5月颁布）中的第二十三条规定，通过数值计算结果分析可知，冒溪煤矿南翼区域充填开采充填率大于85%时，地表建筑物为 I 级损坏，地表移动变形控制效果较好.

由图9～图12及表3可知，充填率为0时地表最大下沉量为1 324.2 mm；充填率80%时地表最大下沉量为311.7 mm；充填率85%时地表最大下沉量为209.9 mm，比充填率80%时下沉量减少33%；充填率90%时地表最大下沉量为148.7 mm，比充填率85%时下沉量减少29%.从以上结果看出，地表下沉量随着采空区充填率的提高而减小，因此，应用充填开采 法可以有效的控制地表移动变形.

3 结论

（1）冒溪煤矿南翼区域充填开采，当充填率为0时，地表变形为IV级损坏；当充填率80%时，地表变形为II级损坏；当充填率85%时，地表变形为I级损坏；当充填率90%时，地表变形为I级损坏.

（2）地表下沉量随着采空区充填率的提高而减小，当充填率大于85%时，地表建筑物为 I 级损坏，控制地表移动变形效果较好.