基于动态预警与选择变异的改进麻雀分类算法

黄金彪，白润才，刘光伟，王 东，刘 威，付 杰

（1. 辽宁工程技术大学 矿业学院，辽宁 阜新 123000；2. 宁夏煤炭基本建设有限公司，宁夏 银川 750004； 3. 辽宁工程技术大学 辽宁省高等学校矿产资源开发利用技术及装备研究院，辽宁 阜新 123000； 4. 辽宁工程技术大学 理学院，辽宁 阜新 123000）

0 引言

随着科学研究与计算工程的发展，分类问题在金融业、医疗诊断、互联网信息挖掘等领域日益突出.BP神经网络因其本身具有非线性映射能力、自适应和自学习能力以及强大的泛化性能等优势，在许多工程领域广泛使用[1]．然而，随着应用范围不断扩大，BP神经网络的局部极小化、收敛速度慢,以及预测、预训练能力矛盾等问题不断暴露．因此，如何获取一种高质量的BP神经网络，使分类问题效率有效提升显得尤为重要．

麻雀优化算法（Sparrow Search Algorithm， SSA）是由XUE J K[2]等提出的一种新型群智能优化算法，灵感来自于麻雀觅食以及逃避捕食者的行为.其优势在于算法含有侦察预警机制，具有良好的全局搜索能力.目前关于麻雀算法的改进多集中在初值的初始化阶段引入混沌映射、在搜索过程中引入正弦搜索策略、在变异方法中利用自适应t分布进行变异，对个体位置进行扰动以跳出局部最优等[3-5]，但在算法的收敛速度与精度上还有待提高．

由于麻雀搜索算法优化性能差，提出一种改进麻雀搜索算法（Coyote Genetic Sparrow Search Algorithm，CGSSA）.采用动态预警机制和震荡衰减选择变异机制结合，增强SSA算法逃逸局部极值与加快收敛的能力；然后再将该算法引入BP神经网络参数优化中，从而找出用于解决特定分类任务的最优BP网络参数．

1 麻雀搜索算法

麻雀搜索算法模拟了麻雀种群的觅食行为，具体流程如下.

步骤1初始化麻雀种群数pop，发现者个数m，预警者个数s，维度D，个体取值上、下限lb、ub，学习率ε，迭代次数Max_iter等.

步骤2麻雀种群随机初始化，t时刻种群内第i个麻雀位置被定义为

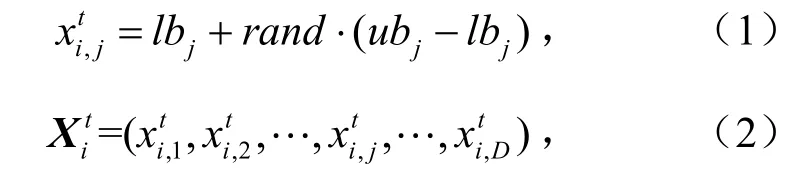
式中，ubj、lbj分别为第j维数值的上、下界；rand为随机生成（0，1）内的实数；xit,j为t时刻种群内i个麻雀个体第j维值，xit为t时刻种群内i个麻雀个体.

步骤3麻雀个体适应能力为

式中，fitit为t时刻种群内第i个麻雀个体的适应度.

步骤4将适应度能力较高的前m个个体作为发现者，剩余（pop-m）个个体作为跟随者；随机选取s个个体作为预警者.

步骤5发现者个体更新[3]为

式中，xit+1为t+1轮迭代中麻雀个体；t为当前迭代次数；Max_iter为最大迭代次数；q为服从标准正态分布的随机数；R2为预警值；ST为安全阈值；L为1×D维的全一矩阵．

步骤6跟随者个体更新为

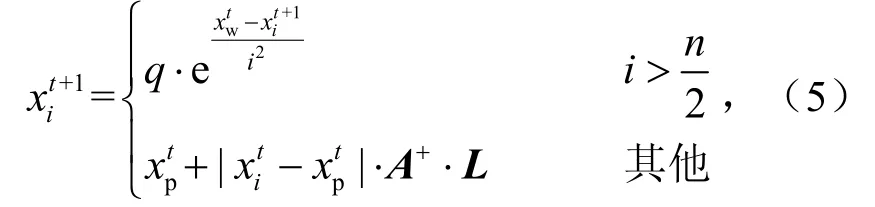
式中，xp为发现者适应能力最优的个体；xw为当前种群中的最差个体；A为1×D维的全一或负一矩阵．

步骤7预警者个体更新[3]为

式中，xtb为种群最优个体；β为步长参数；K为（-1，1）间的随机数；fi、fg和fw分别为当前麻雀、最优麻雀、最坏麻雀的适应度值；ε设置为10．

步骤8记录当前种群个体位置，并计算当前种群个体的适应度.

步骤9个体的选择.

比较当前更新前后麻雀个体适应度值的大小，选择最优适应度值的麻雀个体为

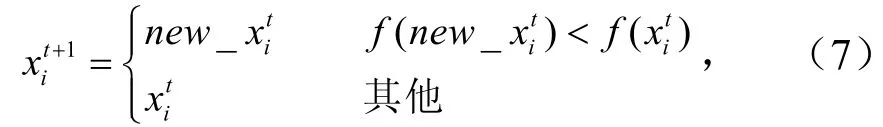
式中，xit更新前麻雀个体，new_xit为更新后的麻雀个体.

步骤10 迭代次数更新.

步骤11 判断终止条件，如果满足，则输出最优麻雀；否则返回步骤4．

2 改进麻雀搜索算法

为进一步提升SSA算法的收敛性能，增加种群的多样性，提出改进思路：采用线性微分递减的方式定义预警者的数量，保持全局搜索与局部开发能力的平衡.再引入变异操作，设置震荡衰减阈值，控制变异操作的发生，将种群中部分较差个体经过变异产生新个体，在保证增大种群多样性的同时提升算法的收敛速度．这种结合动态预警机制与变异操作的改进麻雀搜索算法（CGSSA）的实现细节及算法过程如下.

2.1 预警者数目动态变化

SSA算法的预警者更新过程实际上就是对种群部分个体的二次优化.SSA算法中，预警者数恒定，值设置越大会使算法的全局搜索能力越高，但后期可能会导致算法陷入局部极值，故将预警者数按照线性微分递减[6-7]的规律进行变化，这样既能在算法执行前期提升算法的全局搜索能力，又能在后期优化算法的收敛性，使其尽可能地跳出局部最优.因此，预警者数变化为

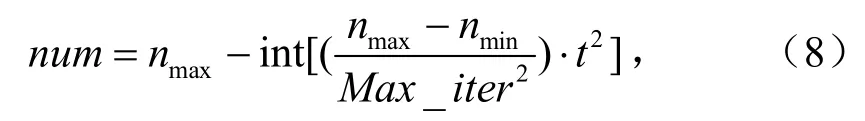
式中，nmax为最大预警者个数；nmin为最小预警者个数；由于预警者个数一般占据种群数的10%～20%，为保证变异机制在算法中的有效性，故设预警者数量变化范围为[nmin，nmax]=[5%pop，20%pop].

2.2 变异操作

在SSA算法中，个体的更新作为提高种群多样性的唯一条件，会使算法对最优解的搜索大概率固定在解空间的某一区域，故其种群多样性不足.在个体更新之后选择性地引入变异操作，将当前时刻下种群适应能力偏低的10%个体进行变异，受到郊狼算法[8]个体更新策略启发，模拟郊狼个体更新策略生成新的变异机制，故个体变异为

考虑到既要保证算法全局与局部寻优性能的平衡，又要保证种群多样性的增加，设定选择执行概率为震荡衰减函数.

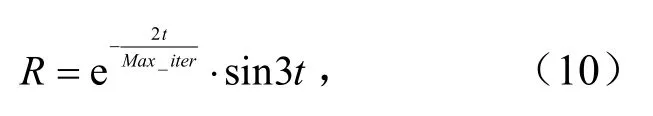
式中，R为选择执行概率的震荡衰减函数.

2.3 算法流程

改进后的麻雀搜索算法流程如下.

步骤1初始化参数包括pop、m、D、lb、ub，ε、Max_iter.

步骤2根据式（1）、式（2）初始化种群.

步骤3根据式（3）计算种群中麻雀个体适应度，并进行排序.

步骤4选取发现者、跟随者，结合式（4）、式（5）分别对发现者、跟随者进行更新.

步骤5根据式（8）计算预警者数量，结合式（6）更新侦察者.

步骤6按照式（9）对种群最差的10%个体进行变异操作.

步骤7对更新后的麻雀个体进行选择，选出适应度较好的组成新的麻雀种群.

步骤8判断是否达到循环结束条件，若达到则进行下一步，否则跳转至步骤3.

步骤9输出最优麻雀个体，算法结束.

3 数值实验

3.1 参数设置

为进一步证明CGSSA的算法性能，采用郊狼算法（COA）、鲸鱼算法（WOAG）[9]、混合灰狼算法（DEGWO）[10]、混合萤火虫和粒子群算法（HFPSO）[11]，以麻雀算法（SSA），这5种算法作对比，选取10组基准测试函数，具体函数信息见表1. f1～f5前5个为多维多峰函数，该类函数具有多个局部最优点，尤其f1函数有多个局部极值和障碍物，f2函数自变量相互影响[12]；f6～f10为多维单峰函数，这些函数的求解难度高，很适合用于测试算法的求解能力和寻优能力．将5种对比算法与CGSSA在10组测试函数上进行算法测试．

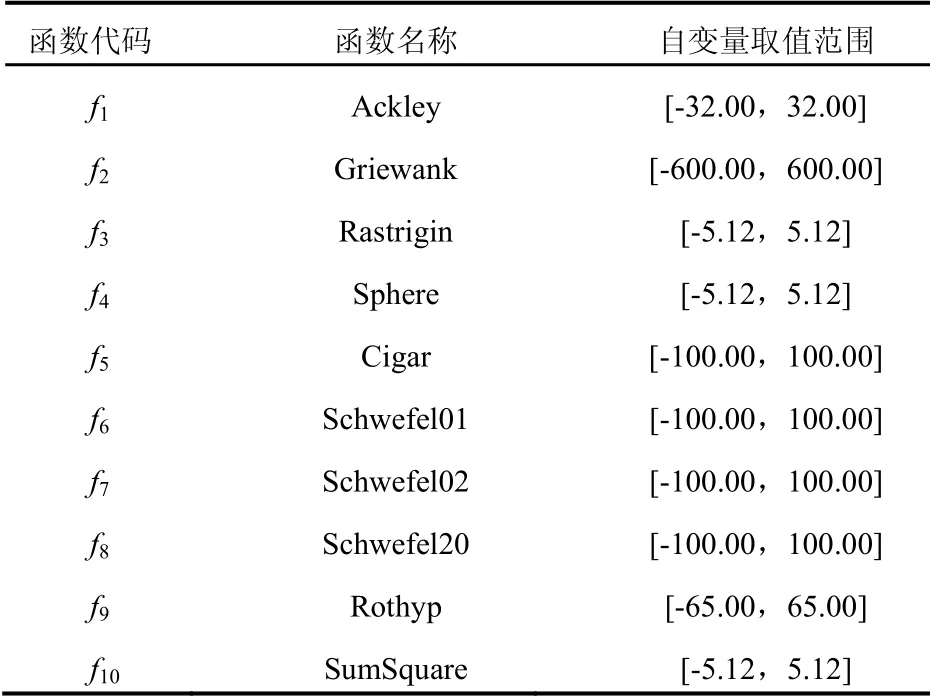
表1 基准测试函数信息 Tab.1 benchmark test function information

为保证实验环境的绝对公平，避免随机性，将所有算法设置相同的公共参数：各算法种群数量pop为100，算法终止条件为1 000×D，各算法的迭代 次数[12]为 Max=ceil((nfevalMax-popsize)/ (popsize+Nc))，5种算法对每一个优化问题分别在D等于30、70维度下均独立进行20次实验．

3.2 结果分析

（1）优化性能

表2为维度为30情况下，CGSSA算法与其他5种对比算法在10个测试函数上的实验结果．

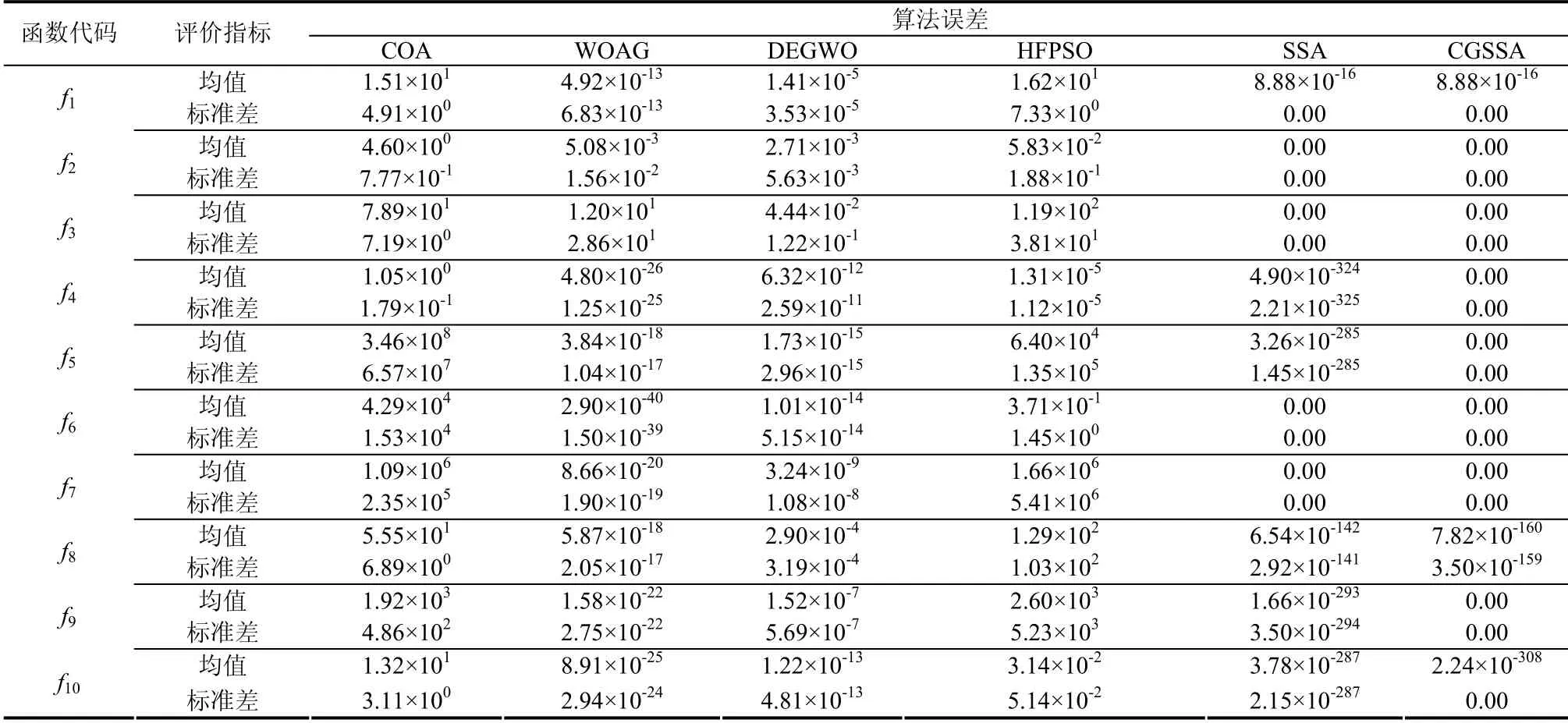
表2 30维度下算法测试结果 Tab.2 algorithm test results under 30 dimensions

由表2可以发现：10个测试函数下的CGSSA算法与其他5种算法的实验结果中，CGSSA算法收敛速度更快，收敛精度及稳定性更加具有优势．CGSSA算法在除f1、f8、f10这3个以外的测试函数上均达到了函数的理论最优解，而在f1、f8、f10函数虽未达到理论最优，但对比其他5种算法的测试结果仍是最优的，故CGSSA算法的寻优精度相较于对比算法更高，更具有优势；同时，从数据结果可以发现CGSSA算法的寻优标准差多次为0，而COA算法、WOAG算法、DEGWO算法，以及HFPSO算法的寻优标准差结果远大于0，故相较于这4种算法CGSSA算法具有更好的稳定性；虽然CGSSA算法对比SSA算法的标准差结果没达到所有函数都是最优，在测试函数f1、f2、f3、f6、f7上二者的标准差相同，即稳定性相同，但在其余5个测试函数上，CGSSA算法占据优势，综合分析，CGSSA算法的稳定性更好，鲁棒性更强．

为进一步证明算法的高维可拓展性，在10个测试函数下，将CGSSA算法与其他5种算法进行维度为70的数值实验，通过对比各算法迭代过程中的最优解均值与算法达到最优解时的收敛次数，对算法进行收敛性分析，结果见表3．

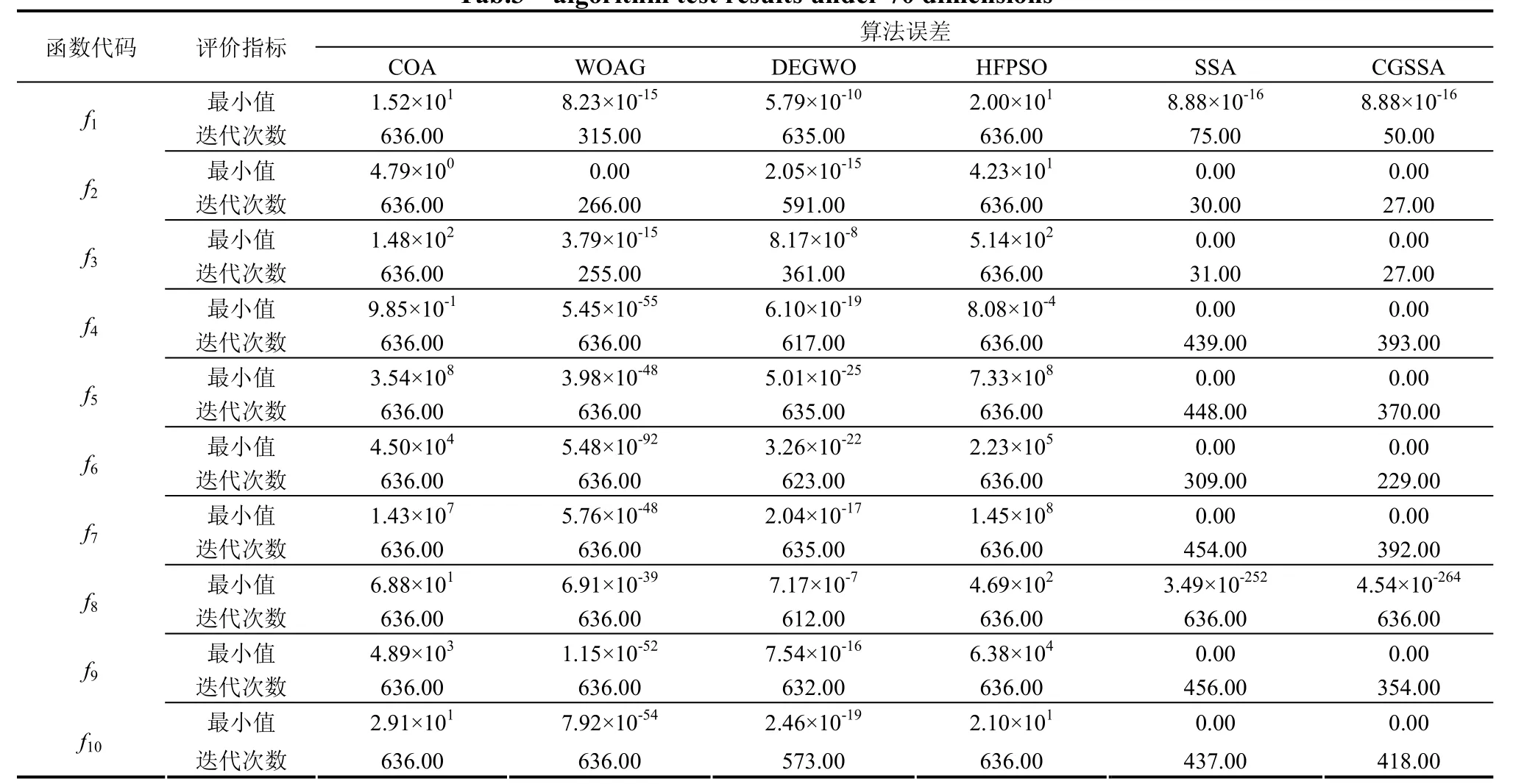
表3 70维度下算法测试结果 Tab.3 algorithm test results under 70 dimensions

如表3，CGSSA算法与SSA算法在除f1与f8以外的测试函数上均达到了函数的理论极值，算法的寻优精度远高于COA、WOAG、DEGW，以及HFPSO算法；在测试函数f8上，CGSSA算法的最优解值小于SSA算法，故该函数条件下，CGSSA算法的寻优精度高于SSA算法；从表3中的Niter评价指标（收敛次数）数据可以发现，除f8以外的9个测试函数上，CGSSA算法与SSA算法虽然均达到了函数的最优解，但CGSSA算法的迭代收敛次数均小于SSA算法，表明CGSSA算法比SSA算法更早地收敛，故CGSSA算法的寻优速度更快.综合分析，5种与其他算法相比，CGSSA算法的寻优精度与收敛速度都具有一定优势，即寻优能力最强.

（2）收敛性能

为更直观地表现出CGSSA算法的寻优速度、精度优势，绘制CGSSA算法与其余5种对比算法在70维度下的10个基准测试函数上的收敛曲线，见图1、图2，图中纵坐标为最优对数适应度值．

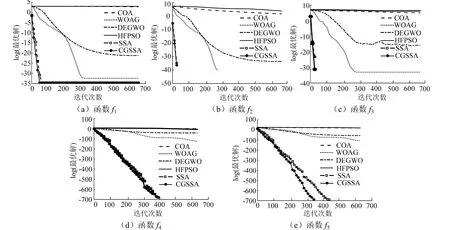
图1 D=70时6种算法的多维多峰函数收敛图率比较 Fig.1 comparison of convergence graphs of multidimensional and multimodal function of the six algorithms at D=70

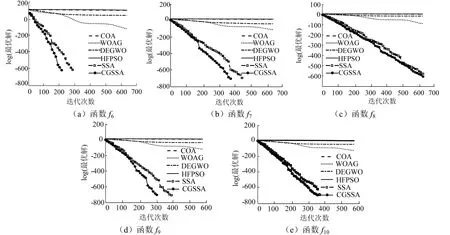
图2 D=70时6种算法的单峰函数收敛图率比较 Fig.2 comparison of convergence graphs of u n imodal functions of the six algorithms at D=70

由图1、图2可见，10个测试函数下，CGSSA算法的收敛速度均优于其他5种对比算法，在测试函数f5、f6、f7和f9上，算法的速度优势尤为明显；同时，CGSSA算法的收敛精度在所有测试函数上均不低于其他对比算法；故CGSSA算法的收敛速度与精度比其余5种算法更具优势．

由上述分析可知，GSSA算法不仅在低维测试环境下具有良好的寻优能力，在高维测试条件下，优化性能也占据优势地位；数值结果与可视化结果充分体现了GSSA算法寻优精度更高、收敛速度更快的特点.实验结果还表明该算法的鲁棒性强，稳定性高.故改进由SSA算法得到的CGSSA算法的优化性能相对较强．

4 基于CGSSA的BP神经网络参数优化

采用常见的机器学习中的分类问题对算法CGSSA进行可行性验证．

BP神经网络的激活函数可令神经网络的每层输出结果非线性化，具有可微性、非线性、单调性等特点，将神经网络的分类问题转化为优化问题，将最大化分类准确率作为优化目标，即优化问题的适应度函数．利用CGSSA优化BP神经网络，进而获得一组较为高效的权值、阈值参数，使神经网络的分类准确率尽可能最大.试验中，将种群规模pop设为25，将BP神经网络的训练次数设置为3 000.将标准神经网络[13]、基于遗传算法[14-16]的神经网络作为对比算法，遗传算法与CGSSA算法的迭代次数均设定为100．采用UCI数据库中的5组分类数据集，实验参数见表4．

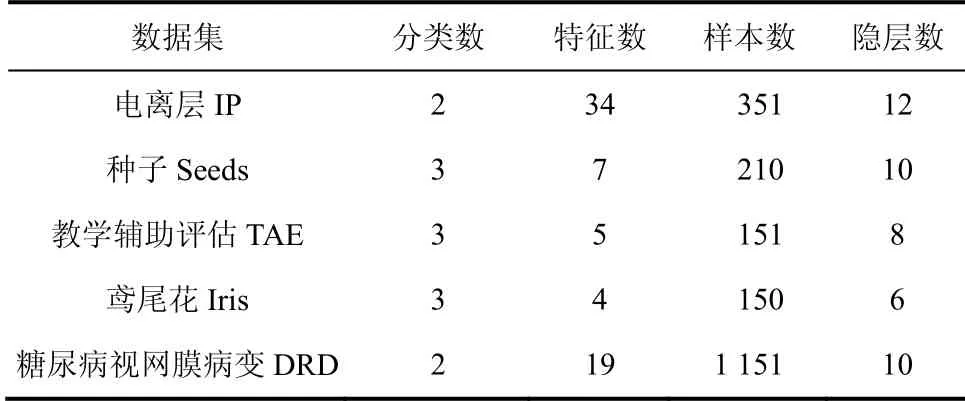
表4 实验中使用的UCI数据集 Tab.4 UCI dataset used in the experiment

为保证实验的有效性，3种算法在5个数据集上分别进行30次实验，记录30次实验得到的测试集的最大值、最小值、标准差、均值作为算法的评价指标；同时，为了进一步分析算法的泛化性能，增加计算训练集与测试集在各算法上的分类准确率差，数据结果见表5.

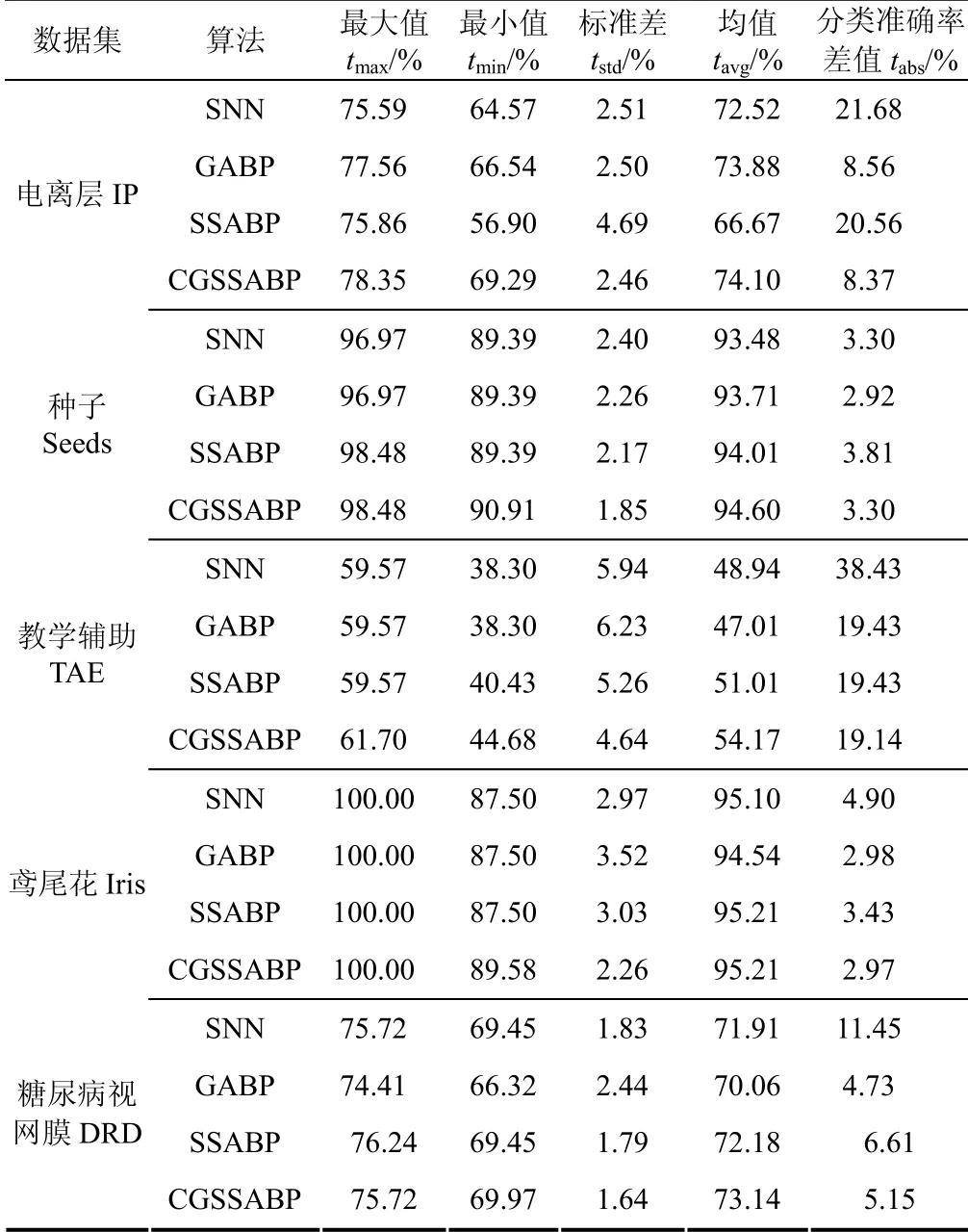
表5 分类准确率测试结果 Tab.5 test results of classification accuracy

如表5，基于CGSSA算法的BP神经网络得到的分类准确率的标准差、最小值、均值在5组数据集上都是最大的，表明基于CGSSA算法的BP神经网络模型具有最小的分类损失、最好的稳定性、最好的平均性能.表5中数据显示，基于CGSSA算法的BP神经网络在4组数据集上的最大值指标结果都是最优的，但是DRD数据集上得到的最大值指标结果与SSABP算法相比不占据优势，结合数据集的信息，这一现象可能是由于测试数据集的样本量较少，结果偶然性比较大导致的，但算法在其他4组数据集上的最大值优势明显，故基于CGSSA算法的BP神经网络仍具有最大的分类效益；此外，基于CGSSA算法的BP神经网络在IP、TAE、Iris数据集上泛化误差数值均低于其他3种算法，泛化性能位列第一，在Seeds、DRD数据集上GABP算法的泛化误差最小，基于CGSSA算法的BP神经网络泛化性能位列第二，但GABP算法的其余指标性能差，故综合分析，CGSSA算法的泛化能力更强．

综上所述，基于CGSSA算法的BP神经网络在机器学习的分类任务中具有最好的分类性能，模型稳定性高，且具有高效的泛化能力．

5 结论

以麻雀优化算法为出发点，结合机器学习中的分类任务，从算法的性能优化角度展开研究，通过数值实验形成如下结论.

（1）为提升麻雀搜索算法的搜索性能，采用线性微分递减方法动态改变麻雀个体更新过程中的预警者数量，进而改变了麻雀个体恒定的更新过程；通过设置震荡衰减阈值选择性的对种群中适应能力较差个体执行变异，提出一种结合动态预警与选择变异的麻雀搜索算法（CGSSA）；数值实验结果表明，CGSSA算法有效提高了原始麻雀搜索算法的寻优精度与收敛速度．

（2）为进一步分析CGSSA算法的应用能力，将CGSSA算法与BP神经网络相结合，提出新的神经网络模型应用于机器学习分类任务，数值实验结果表明：基于CGSSA算法的BP神经网络与SNN算法、GABP算法相比具有更好的分类性能．