岩石分数阶统计损伤流变本构模型

关 顺，王来贵，孙 闯

（1. 辽宁工程技术大学 力学与工程学院，辽宁 阜新 123000；2. 辽宁工程技术大学 土木工程学院，辽宁 阜新 123000）

0 引言

在岩土工程中，岩石的变形、破坏和失稳皆与岩石的非线性流变特性有着紧密的联系[1]，如边坡的蠕变失稳现象、地下结构收敛变形的稳定性评价及煤柱的长期变形等.因为传统线性流变本构模型无法描述这种非线性流变特性，所以必须建立非线性流变本构模型.

目前，在非线性流变本构模型的构建方面，分数阶流变本构模型是研究热点，研究人员对此进行广泛而深入的研究.周宏伟[2]等提出一种新型变黏滞系数分数阶Abel黏壶元件，并应用此模型对盐岩单轴蠕变实验数据进行拟合，此模型弥补西元模型无法描述加速蠕变阶段的缺陷.张向东[3]等进行不同围压下砂岩蠕变实验，发现砂岩的力学特性随围压升高而从脆性转化为延性，并建立相应的损伤本构模型，准确地分析实验蠕变曲线.单仁亮[4]等对不同节理面倾角的红砂岩进行低温蠕变实验，并建立相应的分数阶蠕变模型，此模型的模拟效果优于西元模型.何志磊[5]等根据水电站隧洞开挖时围岩出现的流变劣化现象，基于分数阶导数并考虑蠕变参数的非定常性，建立非线性蠕变本构模型，并根据大理岩剪切蠕变实验结果推演出模型参数.王军保[6]等建立改进分数阶流变本构模型，并通过岩石蠕变实验对模型进行验证.

现有的分数阶流变本构模型通常只与传统损伤理论相结合，无法反映岩石的非均质性及内部缺陷的发展情况.本研究将分数阶微积分理论与统计损伤理论相结合，建立非线性分数阶统计损伤岩石流变本构模型，可以反映岩石内部不规则分布的微裂纹、微孔洞等缺陷在流变过程中扩展、贯通的变化规律[7]，并根据广义胡克定律及Perzyna黏塑性理论推导出三轴压缩应力状态下的蠕变函数，对泥岩进行围压20 MPa下的三轴分级加载蠕变实验，应用该模型对蠕变实验数据进行拟合及参数辨识，以验证该模型的合理性.

1 分数阶弹壶元件

分数阶微积分是对传统微积分的一种推广，在分数阶微积分中，微积分阶数的定义域由整数域扩展到整个实数域及复数域.Riemann-Liouville型（简称R-L型）分数阶导数的定义式[2]为

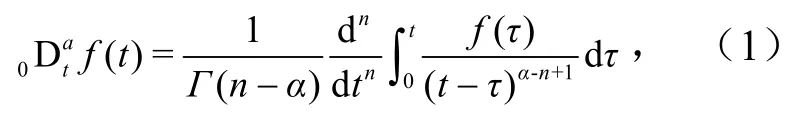
式中，0Dat为分数阶导数运算符，表示对函数取α阶导数；α为分数阶；t为时间，h；n为大于α的最小整数；Γ为Gamma函数.

当函数f(t)在0附近可积时，R-L型分数阶微积分的Laplace变换为

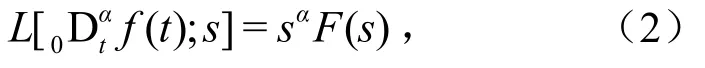
式中，F(s)为f(t)的Laplace变换式.

为准确描述物质的黏弹性，多种分数阶元件被提出.Koeller在Rabotnov的研究基础上，基于R-L型分数阶导数，提出弹壶（spring-pot）元件[8].该元件所受应力与所产生应变的分数阶导数成正比，取式（1）中整数n=1.

与Abel黏壶相比，Koeller弹壶多出一个比例参数γ，因此Koeller弹壶更适合描述复杂的流变性质.弹壶元件具备弹簧元件与牛顿黏壶元件的特点，其分数阶导数阶数α的取值范围为0～1，能够描述从固体到流体间任意状态.由文献[8]可知，当应力取单位值1时，有

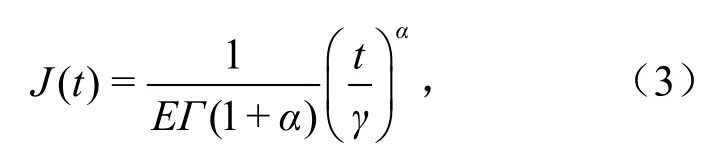
式中，J为蠕变柔量，MPa-1； E为弹性模量，MPa；γ为特征蠕变时间，h.

2 分数阶统计损伤流变本构模型

2.1 一维流变本构模型

为解决传统线性流变本构模型无法描述岩石非线性流变现象的问题，基于分数阶微积分理论及连续介质统计损伤理论建立新型岩石分数阶统计损伤流变本构模型，见图1.

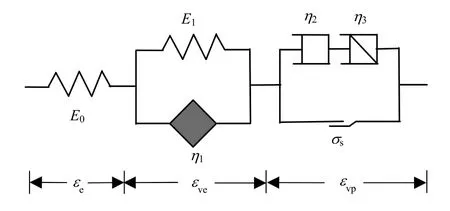
图1 岩石分数阶统计损伤流变本构模型 Fig.1 fractional statistical damage rheological constitutive model of rock

进行一维应力情况下的本构方程推导.由于岩石是一种黏弹塑性材料，因此岩石总的蠕变变形包括3个部分，分别是弹性变形、黏弹性变形及黏塑性变形.由图1可知这3部分互相串联，因此模型的总应变为此3部分应变之和，即

式中，ε为总应变；εe为弹性应变；εve为黏弹性应变；εvp为黏塑性应变.

模型3部分所受的应力大小皆相等.

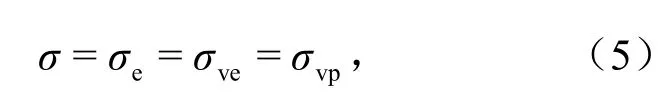
式中，σ为总应力，MPa；σe为弹性应力，MPa；σve为黏弹性应力，MPa；σvp为黏塑性应力，MPa.

流变模型的弹性部分用来描述在施加载荷的瞬间岩石产生的弹性变形，该部分与原有的线性流变模型相同，由一个弹簧元件构成，其本构方程为

式中，E0为弹性部分的弹性模量，MPa. 当应力取恒定值时，由式（6）可得

式中，σ0为取恒定值时的应力，MPa.

流变模型的黏弹性部分用来描述黏弹性变形，由于施加恒定外载荷时黏弹性变形不会随时间无限增长，且卸载后黏弹性变形可以随时间恢复，因此取文献[8]中包含Koeller弹壶的分数阶Kelvin体作为本模型的黏弹性部分，其本构方程为

式中，E1为黏弹性部分弹簧元件的弹性模量，MPa；η1为弹壶元件的黏滞系数，MPa·h.

当应力取恒定值时，对式（8）两端进行分数阶Laplace变换，经整理得

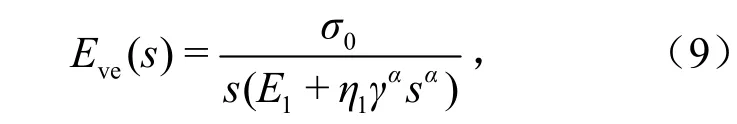
式中，Eve为黏弹性应变εve的象函数.

再经分数阶Laplace逆变换，可得黏弹性部分蠕变函数为

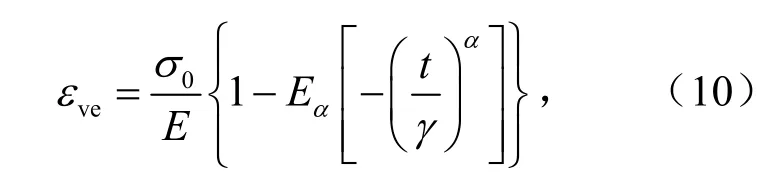
式中，Eα为Mittag-Leffler函数，其定义为

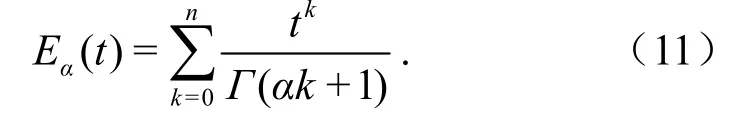
流变模型的黏塑性部分用来描述当外载荷高于应力阈值时试样产生不可恢复的变形，该部分由Bingham体改进而来.改进方法为：在Bingham体中添加一个变黏滞系数损伤黏壶元件，使之与Bingham体中原有的牛顿黏壶相串联.Bingham体原有牛顿黏壶负责描述等速蠕变阶段，损伤黏壶则用来描述加速蠕变阶段，则黏塑性部分的本构关系可表示为

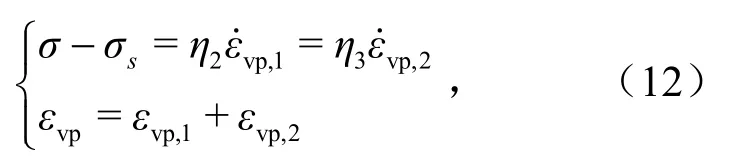
式中，σs为应力阈值，MPa；η2为牛顿黏壶的黏滞系数，MPa·h；η3为损伤黏壶的黏滞系数，MPa·h；εvp,1为牛顿黏壶的应变；εvp,2为损伤黏壶的应变；为黏塑性应变速率；为黏塑性应变速率.

当应力取恒定值时，通过解微分方程组（12）可得黏塑性部分的蠕变函数为

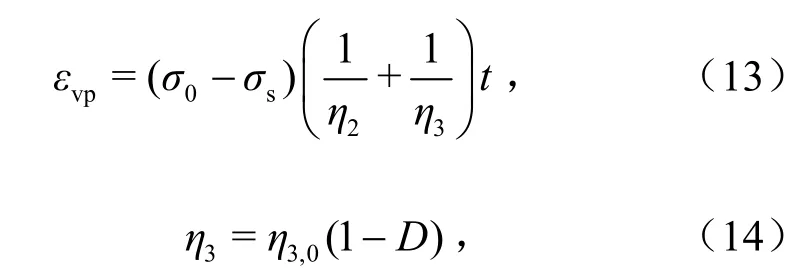
式中，η3,0为岩石试件未发生损伤时的黏滞系数，MPa·h；D为损伤变量；η3会随着D的增加而减小，从而使蠕变速率随时间增长，可描述加速蠕变现象.

假设仅当岩石所受载荷高于应力阈值时岩石发生损伤，损伤变量的变化规律服从统计损伤理论，该理论将宏观的岩石块体看作由大量岩石微元组合而成[9]，由于岩石的非均质性，这些岩石微元的强度各不相同.岩石微元共具有两种状态，即完整状态和破坏状态.当岩石微元受外载荷作用时，强度低于这一外载荷的微元全部发生破坏，而强度高于此外载荷的微元则保持完整，根据统计损伤理论，损伤变量定义为已破坏的微元数量与总微元数量之比，即

式中，Nd为破坏的微元数；N为总微元数.

在流变过程中，随着时间的增长，不断有岩石微元发生破坏，假设Nd是时间的函数，同时损伤变量也逐渐增大.根据文献[9]，岩石微元的强度大小通常被假定服从某一概率分布，对岩土材料而言，应用Weibull分布较为合理，则破坏的岩石微元数量表示为Weibull分布函数与总微元数的乘积对时间的积分，即

2.2 三维流变本构模型

为描述岩石在三维应力状态下的流变变形规律，需要建立三维流变本构模型.在一维流变本构模型的基础上推广到三维情况，并假定岩石为各向同性.与一维流变本构模型相同，三维流变本构模型的总应变也为弹性、黏弹性及黏塑性三部分之和，用张量分量形式可表示为

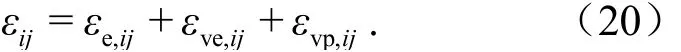
在三维应力情况下，应力张量分解为

式中，σm为静水压力，MPa；Sij为偏应力张量，MPa；δij为Kronecker符号，当2个下标相同时，等于1，当2个下标不同时，等于0.静水压力为

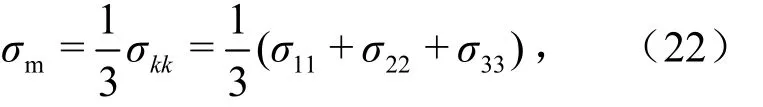
式中，σkk为体积应力，MPa，决定弹性体积变形.

与应力张量类似，应变张量也可分解为与体积变化相关的部分以及与畸变相关的部分.

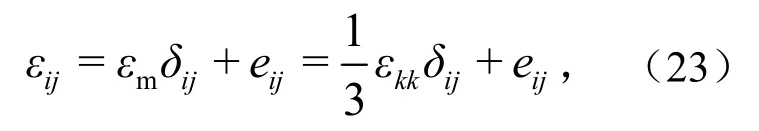
式中，εm为静水应变；eij为偏应变；εkk为体积应变.

根据广义胡克定律，模型第一部分的变形为

式中，K0为体积模量，MPa；G0为剪切模量，MPa.

当应力不变时，弹性应变为

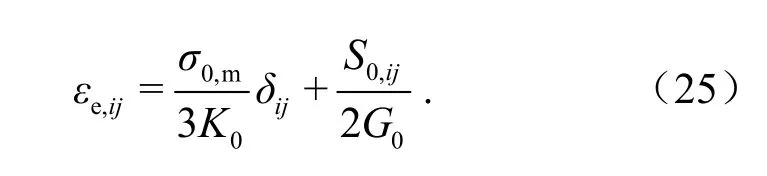
假设体积变形为纯弹性，黏弹性变形与黏塑性变形仅由偏应力引起，黏弹性蠕变函数可由式（10）替换参数获得，根据文献[9]中所述的方法，用2G1及S0,ij分别替换E1及σ0得

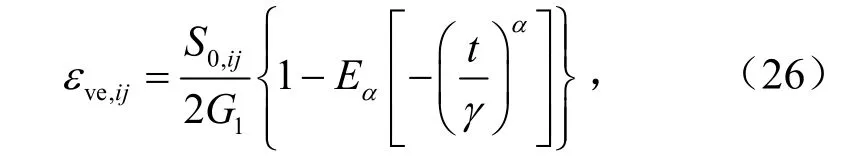
式中，G1为黏弹性部分弹簧元件的剪切模量，MPa.

对于模型的黏塑性部分，将式（18）推广到三维应力情况，根据Perzyna黏塑性理论[10]得

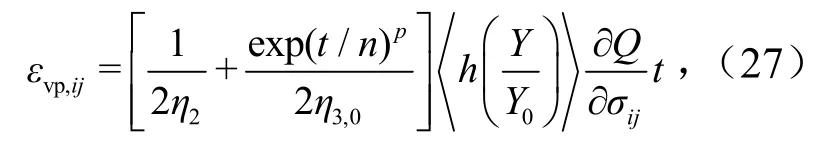
式中，h为过应力函数，通常可假定为幂函数，对于岩土材料，可取幂函数的指数为1[11]；Y为屈服函数；Q为塑性势函数；Y0为常数.过应力函数的取值法则为

可见，只有当屈服函数不小于0时，才会发生黏塑性变形.在常温条件下，静水压力对岩石的流变变形影响较小，流变变形主要受偏应力影响[9].因此，可假设岩石材料服从Mises屈服准则为

式中，J2为偏应力张量第二不变量，MPa.

采用关联流动法则，有Q=Y.

当岩石试件处于三轴压缩时，有σ2=σ3.联立式（20）、式（25）、式（26）及式（27），推导出三轴压缩状态下的蠕变函数为

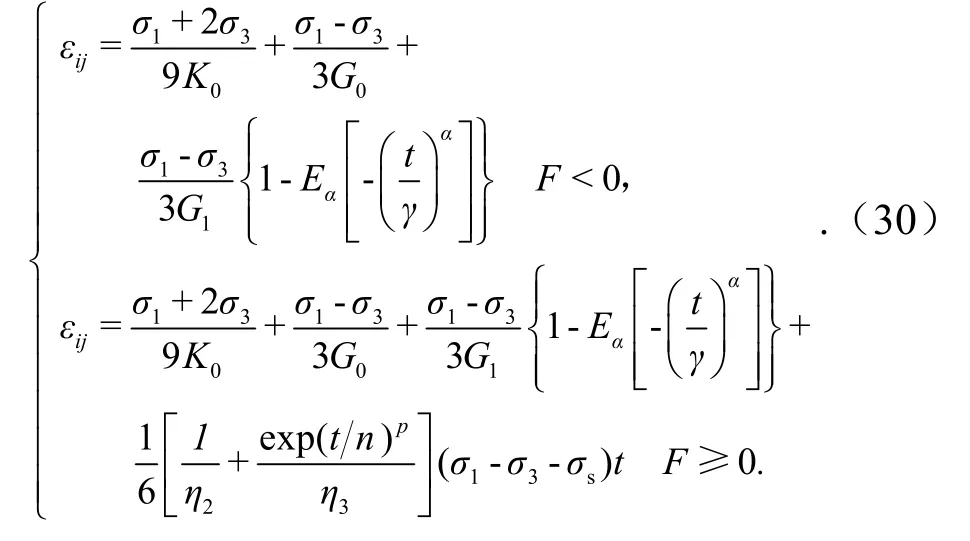
3 岩石蠕变实验及模型参数辨识

实验所用岩样为泥岩，试件规格为Φ50 mm ×100 mm.实验所用的仪器为GDS高精度软岩流变仪，其围压为0～32 MPa，轴压为0～250 kN.岩石试样及实验仪器见图2.

图2 泥岩试件及实验仪器 Fig.2 mudstone specimen and experimental instrument

实验步骤为：①装载试件，将试件固定在仪器底座上，在其外部包裹一层热缩管，用热风枪吹缩.为防止围压硅油浸润试件引起实验误差，对试件两端进行密封.②将LVDT位移传感器固定在试件上，再将压力室闭合.③将围压加载至20 MPa，施加轴向载荷进行三轴分级加载蠕变实验，全部加载级别的蠕变实验皆在20 MPa围压下进行.在前6级加载中，每级偏应力增量为6.64 MPa，最后1级偏应力增量为5.72 MPa.由于采用的加载方法是分级加载，在曲线拟合之前需根据叠加原理将分级加载型蠕变数据转换为分别加载型蠕变数据，转换后的蠕变数据见图3.

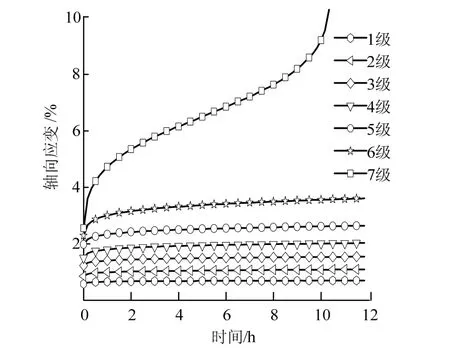
图3 不同加载型蠕变实验数据 Fig.3 different loaded type creep experiment data

对于前6级加载，由于载荷未达到产生塑性变形的应力阈值，因此只发生减速蠕变.在发生瞬时弹性变形后，蠕变速率（蠕变曲线的切线斜率）随时间增长而逐渐减小.当进行第7级加载时，首先发生减速蠕变，蠕变速率逐渐减小；t=2 h时，蠕变速率不再减小，转为等速蠕变，在此阶段，蠕变速率近似保持不变；t=8 h时进入加速蠕变阶段，蠕变曲线呈指数型上扬形态，在此阶段，蠕变速率随时间增长而急剧增大，岩石试件最终发生破坏.

为验证上文所建立的分数阶统计损伤流变本构模型的合理性，应用其对泥岩蠕变实验数据进行拟合，并求得模型参数.由于前6级加载皆为同类型的减速蠕变曲线，因此取第1级蠕变曲线作为减速蠕变代表进行拟合.而第7级蠕变曲线包含典型蠕变的全部3个阶段，因此必须要对其进行拟合，以验证所建立的本构模型是否能够准确描述蠕变的3个阶段.式（31）中的应力阈值可取岩石的长期强度，而长期强度可由等时曲线法[12]获得，本实验的长期强度为35 MPa.然后应用分数阶统计损伤流变本构模型的三维蠕变函数（式（31））对实验数据进行拟合，解得的模型参数及拟合相关系数R2见表1.

表1 模型参数及拟合相关系数 Tab.1 model parameters and fitting correlation coefficient

如图4，拟合曲线与实验数据契合程度较高，拟合相关系数为0.995 8，这表明分数阶统计损伤本构模型能够准确地描述减速蠕变阶段.见图5，无论对于瞬时弹性变形、减速蠕变阶段还是对等速蠕变及加速蠕变阶段，第7级加载的拟合曲线皆与实验数据高度吻合.拟合相关系数为0.997 9，这表明所建立的分数阶统计损伤本构模型不仅能够准确地描述减速及等速蠕变阶段，而且能够精准地描述加速蠕变阶段，此模型弥补了传统线性流变模型无法描述加速蠕变阶段的缺陷.

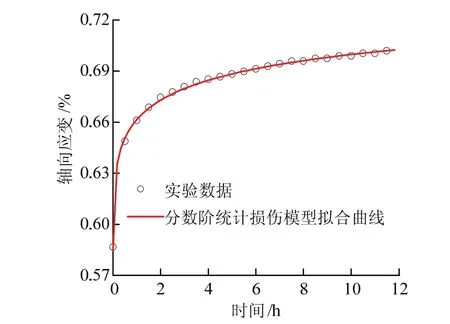
图4 第1级加载拟合 Fig.4 fitting of the 1st step loading

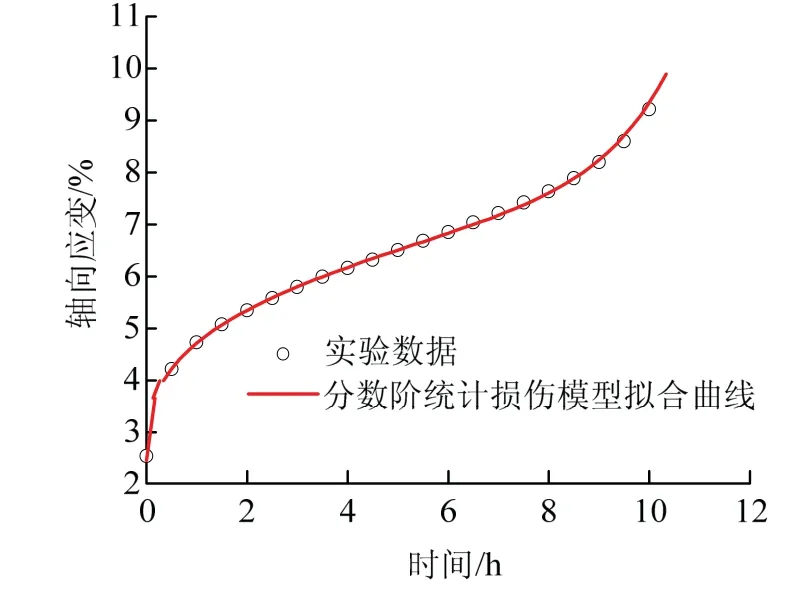
图5 第7级加载拟合 Fig.5 fitting of the 7th step loading

4 结论

基于微分方程型岩石流变本构模型，通过引入koeller弹壶元件及统计损伤黏壶元件，构建了一种新型岩石流变本构模型，并推导出该模型在一维及三维应力状态下的蠕变方程，根据非线性最小二乘法对泥岩蠕变实验数据进行拟合，获得了模型参数.根据上述研究内容，可得出以下结论.

（1）将koeller分数阶弹壶引入到模型构建中，能够表示弹簧与牛顿黏壶元件之间的任意状态，只需一个弹壶元件就能准确模拟岩石的黏弹性，可在一定程度上减少参数数量.

（2）引入统计损伤黏壶元件描述加速蠕变，使该元件的黏滞系数变化规律服从统计损伤理论，其优点在于能够反映岩石微元强度的随机性，阐释了蠕变过程中岩石内部的损伤机制.此外，将一维应力下的流变模型推广到三维应力状态下也拓宽了模型的适用范围.

（3）某些岩石流变本构模型通过分段函数描述岩石的加速蠕变阶段，需要拟合2次，这样会增加计算的复杂性.本文建立的新型分数阶统计损伤流变本构模型无需分段，整体性更强，在数据拟合方面更加便捷.在对泥岩实验数据进行拟合分析时，拟合相关系数在0.995 8～0.997 9之间.可见，该模型的拟合效果良好，对蠕变的3个阶段皆有准确的描述.