超高速PMSM电磁性能解析解及转子设计

程文杰， 曹广东， 邓志凯， 肖玲， 李明

(西安科技大学 理学院，西安710054)

0 引 言

采用高速、超高速永磁同步电机(permanent magnet synchronous motor，PMSM)直接驱动透平机械是21世纪新一代旋转机械提高功率密度、机组效率和改进机组性能的发展方向。高速、超高速电机已经广泛应用于燃料电池、透平压缩机、储能飞轮和分布式发电等领域[1]。鉴于有限元法(finite element method, FEM)能考虑许多复杂的因素，比如磁饱和、端部效应、磁滞等，其被普遍用来预测电机的电磁性能。但是FEM在设计初期比较耗时，移植性差，并且缺少解析解那样的洞察力。解析解计算快，适用于优化设计[2-3]。

高速、超高速永磁同步电机一般采用极弧数为1的两极表贴式转子，或者实心圆柱永磁体转子。Z.Q.Zhu似乎最早表现出对这种转子的关注[4]，作者指出当时已知的解析方法不适用于描述这种转子励磁磁场。随后Z.Q.Zhu在文献[5]里面给出了忽略定子槽效应下，上述转子的开路静态磁场解析表达式。实际上，定子齿槽效应对气隙磁场的影响非常大，在高速、超高速永磁电机设计中必须予于考虑。文献[6]推导了平行充磁的“永磁体环+导磁芯轴”转子和实心圆柱永磁体转子开路静态磁场解，采用基于保角变换的气隙磁导函数描述定子槽效应。文献[7]计算了组合双层Halbach永磁转子励磁磁场，采用卡特系数描述定子齿槽效应。但是气隙磁导函数和卡特系数在描述气隙磁密周向分量时尚存在问题。另一种考虑槽效应的方法称为子区域法，即直接求解电机各个子区域内的控制方程，然后根据边界条件和子区域之间的交界条件获得磁场的解。值得注意的是在采用子区域法时，有些文献研究对象为单槽或者单极模型，因而在某种程度上忽略了槽开口之间的相互影响。文献[8]首次提出了精确子区域模型，能够考虑定子槽开口之间的互相影响。文献[9]采用精确子区域法求解了半闭口定子槽，极弧系数小于1的表贴式PMSM的磁场解析解。文献[10]采用精确子区域法推导了任意充磁方式表贴式PMSM磁场解析解，但是模型仅仅针对非叠绕绕组，没有考虑叠绕绕组的情形。文献[11]提出的解析模型能描述半闭口槽、双层叠绕绕组，但是针对的是四极及以上的永磁转子。国内对表贴式PMSM电磁性能的解析研究进展较快，但主要针对的是低速转子或者极弧系数小于1的转子[12-15]。文献[16-17]采用子区域法对更复杂的模型进行了计算，考虑了铁心磁饱和。高速、超高速永磁电机的设计涉及到多个学科，是系统设计的代表。文献[18]针对一台75 kW，60 000 r/min的高速永磁电机，基于应力场、电磁场和温度差对转子护套进行了综合设计。文献[19]采用有限元法，基于多物理场耦合，提出了一套完整的高速转子优化设计方法。

为减弱谐波，高速、超高速PMSM通常采用双层叠绕、短距线圈定子和极弧数为1的平行充磁的两极转子。而目前鲜见这类电机电磁性能的解析研究报道。特别地，为了达到设计转速，在电磁性能计算的同时还需兼顾转子动力学性能。为此，本文将考虑双层叠绕线圈和半闭口槽，采用精确子区域法解析预测超高速PMSM电磁性能，设计两款不同结构的高速转子，校核其临界转速，并总结此类超高速转子的设计特点。

1 解析模型

超高速永磁同步电机模型如图1所示，其求解区域划分成5个子区域，分别为：Ⅰ芯轴；Ⅱ永磁体；Ⅲ气隙；i槽开口；J1槽顶区域；J2槽底区域。电机的尺寸含义见图1，其中：θi为第i个槽开口的角度坐标；ΦM0为永磁体磁化方向的角度坐标。

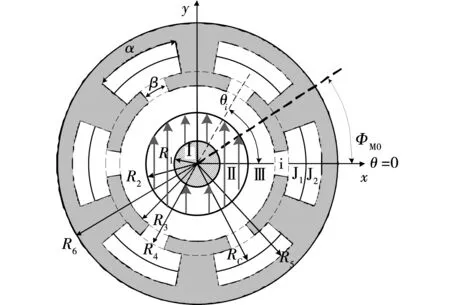
图1 超高速永磁同步电机横截面示意图Fig.1 Cross section of ultra high speed PMSM

为推导方便，作如下假设：

1)定子铁心和导磁芯轴的磁导率为无穷大；

2)永磁体具有线性的退磁曲线，对于稀土永磁材料而言这一假设是合理的；

3)忽略端部绕组效应；

4)槽开口和定子槽形状为径向扇形结构；

5)忽略定子涡流和转子涡流的影响。

1.1 定子槽区域控制方程及通解

第i个定子槽，J1和J2区的控制方程分别为：

(1)

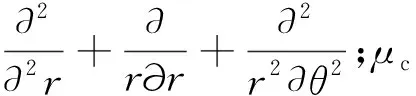
式(1)的通解为对应的齐次方程(拉普拉斯方程)的通解加上非齐次方程(泊松方程)的特解。J1区和J2区的通解分别如下：

(2)

(3)

其中：En=nπ/α；Fm=mπ/β。磁通密度与矢量磁位之间的关系为：

(4)

J1区域，槽两侧磁通密度应满足：

(5)

J2区域，槽两侧和槽底磁通密度应满足：

(6)

联立式(3)、式(4)和式(6)，求出J2区域的磁通密度表达式为：

(7)

(8)

式中：BJi2r为第i个定子槽，J2区径向磁通密度；BJi2θ为第i个定子槽，J2区周向磁通密度。其它角标的意义与之类似，后面不再单独说明。Gc5(n)是只与n相关的函数。

联立式(2)、(4)和(5)，求出J1区域的磁通密度表达式：

(9)

(10)

可见，通过引入边界条件后，J2区域磁通密度表达式中待定系数为BJi2n，而J1区域的为AJi1n、BJi1n和CJi10。

1.2 槽开口区域控制方程及通解

第i个槽开口子域中的控制方程为

(11)

其边界条件可表示为：

(12)

考虑到边界条件(12)后，式(11)的解可以简化为

(13)

于是第i个槽开口子域中的磁通密度为

(14)

(15)

其中待定系数为Aiim、Biim、Cii0和Dii0。

1.3 气隙区域控制方程及通解

气隙子域的拉普拉斯方程为

▽2AⅢ=0，(0≤θ≤2π)。

(16)

式(16)的通解为

(17)

气隙区域的磁通密度为：

(18)

(19)

式中AⅢk、BⅢk、CⅢk、DⅢk、CⅢ0和DⅢ0为待定系数。

1.4 永磁体区域控制方程及通解

永磁体子域的控制方程为

(20)

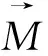
(21)

式中：μ0为真空磁导率；μⅡr为永磁体的相对磁导率。HⅡθ和HⅡr为永磁体内部的周向和径向磁场强度，能反应出定子绕组激励和永磁体激励的叠加效果。另外有：

(22)

如果忽略永磁体内部的涡流，则永磁体内的磁场为无旋场，即电枢反应磁场与永磁体自身励磁磁场的叠加。于是，与气隙磁通密度类似，永磁体内的磁通密度可以记为：

(23)

(24)

式中AⅡk、BⅡk、CⅡk、DⅡk和CⅡ0为待定系数。

2 交界条件

为了求解上述各个子区域内的待定系数，还需要利用子区域之间的交界条件，使得方程组最终封闭。

2.1 定子槽J1和J2区交界面

如图1所示，槽顶和槽底区域满足：

(25)

将式(7)～式(10)代入到式(25)，J1区的磁通密度可以表示为：

(26)

(27)

其中G5c(n)，G4c(n)是只与n相关的函数。由式(26)、式(27)可见，J1区的磁通密度只有待定系数BJi2n。另外，J1区的矢量磁位可以简化为

(28)

2.2 定子槽区和槽开口区交界面

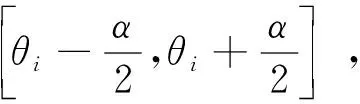
(29)

其中：

(30)

(31)

对于周向磁通密度，有

BJi1θ|r=R4=Bijθ。

(32)

由式(32)，可以得到

(33)

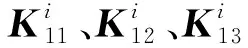
K11BJ2+K12Ai+K13Bi=Y1。

(34)

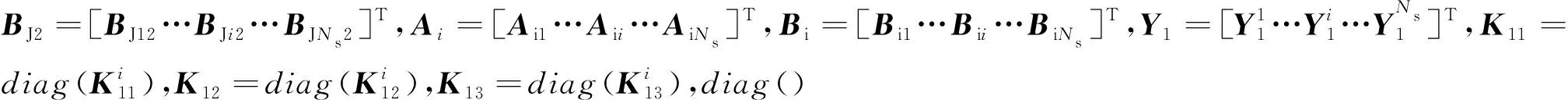
(35)

其中：

(36)

(37)

对于矢量磁位有

AJi1|r=R4=Azii|r=R4。

(38)

将式(35)和式(13)代入式(38)，可以得到

(39)

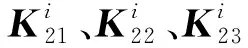
K21BJ2+K22Ai+K23Bi=Y2。

(40)

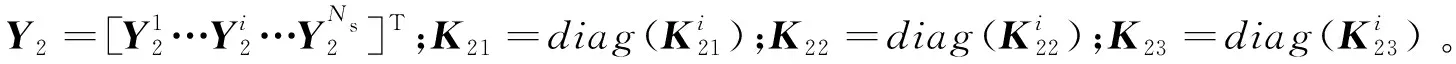
2.3 槽开口区与气隙子区交界面

将r=R3处所有Ns个槽开口区的周向磁通密度Bi1θ～BiNsθ扩展至气隙区域，记为

(41)

其中：

(42)

(43)

(44)

对于周向磁通密度，有

(45)

将式(19)和式(41)代入式(45)后，得：

K32Ai+K33Bi+K34AⅢ+K35BⅢ=Y3；

(46)

K42Ai+K43Bi+K46CⅢ+K47DⅢ=Y4。

(47)

其中K32、K33、K34、K42、K43、K46和K47为已知矩阵，Y3和Y4代表激励向量。待定系数组成的向量分别为：

AⅢ=[AⅢ1…AⅢk…AⅢK]T；

BⅢ=[BⅢ1…BⅢk…BⅢK]T；

CⅢ=[CⅢ1…CⅢk…CⅢK]T；

DⅢ=[DⅢ1…DⅢk…DⅢK]T。

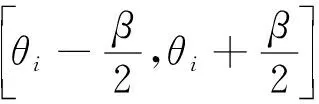
(48)

其中：

(49)

(50)

这里r=R3处气隙区与槽开口区在交界面上的矢量磁位应相等，即

AⅢ|r=R3=Azii|r=R3，(i=1,2，…，Ns)。

(51)

将式(48)和式(13)代入式(51)，得到

K52Ai+K53Bi+K54AⅢ+K55BⅢ+K56CⅢ+K57DⅢ=Y5。

(52)

其中：K52～K57为已知矩阵；Y5代表激励向量。

2.4 气隙区与永磁体区交界面

在r=R2处，应有：

(53)

(54)

将式(19)和式(24)代入式(54)得到：

K64AⅢ+K65BⅢ+K68AⅡ+K69BⅡ=Y6；

(55)

K76CⅢ+K77DⅢ+K7，10CⅡ+K7，11DⅡ=Y7。

(56)

其中：K64、K65、K68、K69、K76、K77、K7，10和K7，11为已知矩阵；Y6和Y7代表激励向量。AⅡ=[AⅡ1…AⅡk…AⅡK]T，BⅡ=[BⅡ1…BⅡk…BⅡK]T，CⅡ=[CⅡ1…CⅡk…CⅡK]T，DⅡ=[DⅡ1…DⅡk…DⅡK]T，为待定系数组成的向量。

将式(23)和式(18)代入到式(53)中得：

K84AⅢ+K85BⅢ+K88AⅡ+K89BⅡ=Y8；

(57)

K96CⅢ+K97DⅢ+K9，10CⅡ+K9，11DⅡ=Y9。

(58)

其中：K84、K85、K88、K89、K96、K97、K9,10和K9,11为已知矩阵；Y8和Y9代表激励向量。注意到，在上面对径向磁通密度的处理中，式(53)中并没有出现Mr，这意味着式(53)中的BⅡr|r=R2已经包括了永磁体自身励磁所产生的径向磁通密度。所以，最后用式(23)表示永磁体内的径向磁通密度，而用式(21)表示永磁体内的周向磁通密度。

2.5 永磁体区与转轴区交界面

如果转子引入导磁芯轴，则用下式表达为

HⅡθ|r=R1=0。

(59)

如果转子采用实心圆柱永磁体，则用下式描述为：

HⅡr|r→0=HⅡθ|r→0≠∞。

(60)

现以含有导磁芯轴的转子为例，将式(21)代入到式(59)得到

BⅡθ|r=R1-μ0Mθ=0。

(61)

将式(22)和式(24)代入式(61)得到：

K10，8AⅡ+K10，9BⅡ=Y10；

(62)

K11，10CⅡ+K11，11DⅡ=Y11。

(63)

其中：K10,8、K10,9、K11,10、K11,11为已知矩阵；Y10和Y11代表激励向量。含有实心圆柱永磁体的转子的推导过程与之类似，不再赘述。

2.6 方程组装

将式(34)、式(40)、式(46)、式(47)、式(52)、式(55)、式(56)、式(57)、式(58)、式(62)和式(63)组装在一起，写成如下一个大方程。解出该方程的系数向量，代回至原来的表达式中，得到各个区域的磁通密度值。

3 电磁性能计算与有限元验证

以一台120 000 r/min超高速永磁电机样机为例，并与FEM结果进行对比，样机参数见表1。

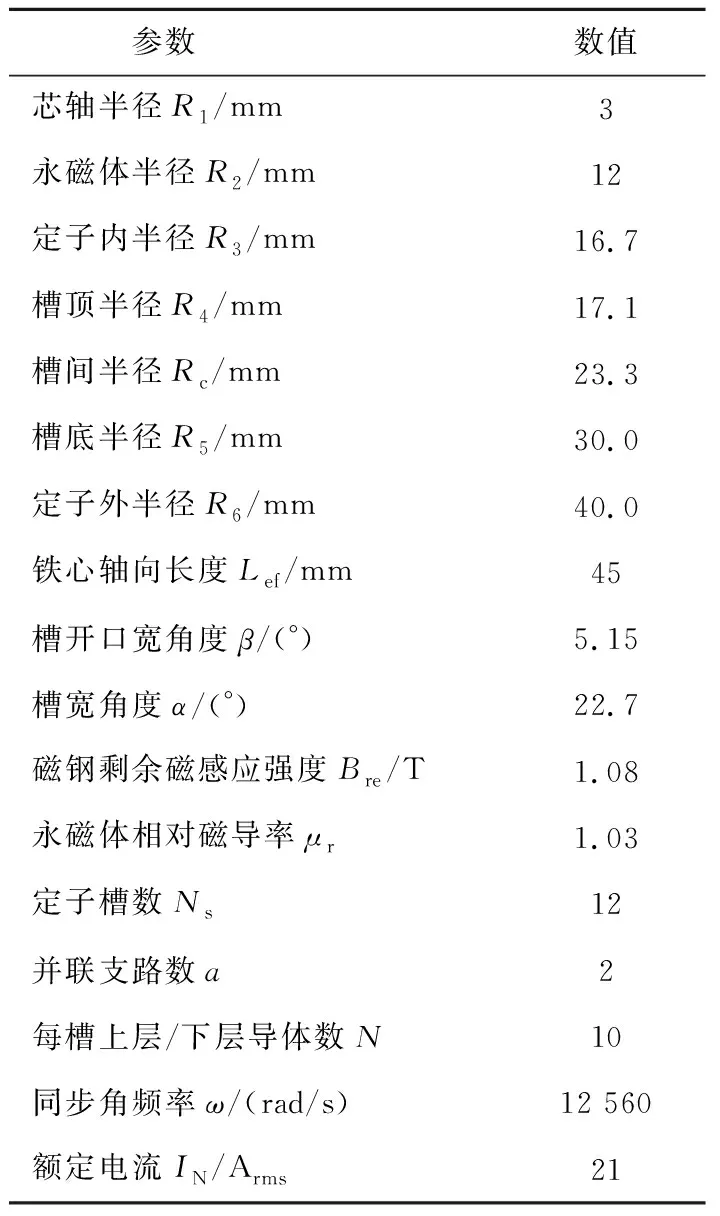
表1 仿真模型的参数

3.1 电枢反应磁场

在求解电枢反应磁场时，将剩余磁感应强度Bre设为0，定子通式所示三相交流电为：

(64)

式中ΦI0为线圈电流的初始相位角。采用双层短距绕组，短距比5/6，布线方式记为：

(65)

式中：I1为槽顶层的电流分布；I2为槽底层的电流分布。根据表1的参数，I1和I2的幅值为300 A。式(1)中Ji1=I1(i)/S1，Ji2=I2(i)/S2，S1和S2分别是槽顶层线圈和槽底层线圈的横截面积。

如图2所示，电枢反应磁场的解析解和有限元解吻合。图2(a)和2(b)显示，在靠近槽开口的气隙区，齿槽对气隙磁密的影响非常显著；而在远离槽开口的气隙区，磁通密度呈现标准的正弦或余弦形状，几乎不受到齿槽效应的影响，如2(c)所示。

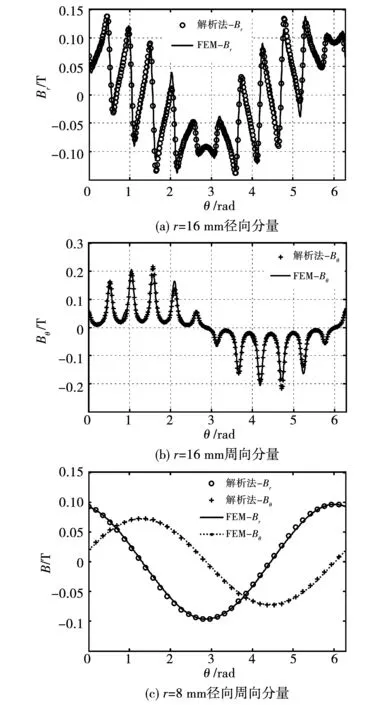
图2 电枢反应径向和周向磁通密度Fig.2 Radial and tangential components of armature reaction magnetic flux density

一般硅钢片的线性段范围约在0～1.8 T，对于算例，额定电流激励时，硅钢片的最大磁密约1.22 T，当取2倍额定电流激励时，最大磁密约为1.88 T，局部区域已基本饱和。在定子铁心磁导率无限大的假设中，电枢反应磁密幅值与电流值成线性关系，当定子铁心出现严重磁饱和时，该线性关系失效，模型会产生较大误差。因此，定子齿宽和轭部宽度应合理选择，以便电机在过载时能产生足够的力矩。

3.2 永磁体磁场

在求解永磁体磁场时，将剩余磁感应强度Bre设为1.08 T，式(64)中IA=IB=IC=0。求解结果如图3所示。

图3所示，永磁体磁场的解析解和有限元解吻合。在r=16 mm处，永磁体磁场的径向磁通密度幅值约为0.55 T，周向磁通密度幅值约为0.065 T，周向磁密要比径向磁密小一个数量级，如图3(a)和图3(b)所示。对比图2(a)和图3(a)，电枢反应磁场径向磁密的幅值约为永磁体磁场的26%。

图3 永磁磁场径向和周向磁通密度Fig.3 Radial and tangential components of PM magnetic flux density

3.3 负载磁场

调整ΦI0和ΦM0，使得永磁体磁场竖直向上，电枢反应磁场竖直向下，即电枢反应磁场只有去磁作用，对应的负载磁场结果如图4所示。如图4(a)所示，r=16 mm处，负载磁场的径向磁密幅值约为0.43 T，要比永磁体磁场对应的幅值小。对比图2(a)、图3(a)和图4(a)，发现负载磁场的径向磁密波形正弦度要优于电枢反应磁场，而劣于永磁体磁场，这是于事实相符的。对比图2(b)、图3(b)和图4(b)，发现负载磁场的周向磁密波形接近于电枢反应磁场。这是因为气隙越靠近定子内径，周向磁密越小。如果不考虑齿槽效应，周向磁密在定子内径处为0，而在相同半径处，永磁体磁场比较弱，对负载磁场的贡献小。

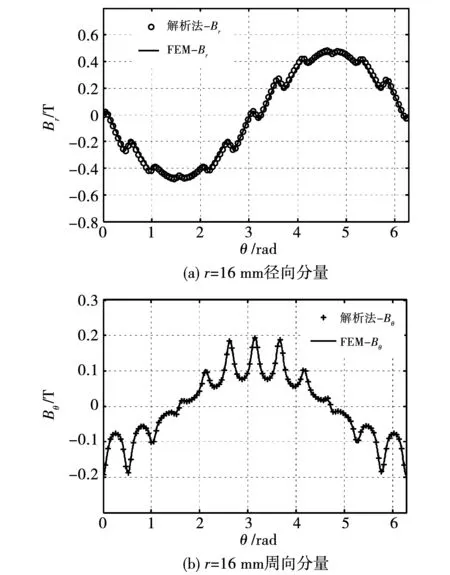
图4 负载磁场径向和周向磁通密度Fig.4 Radial and tangential components of load magnetic flux density

由电机空载、电枢反应和负载下的气隙磁感应强度波形对比可得，采用傅里叶级数法的精确子域解析模型与有限元法计算结果非常吻合。

3.4 空载反电动势

空载反电动势的幅值可以由下式计算得到：

E0=4.44fkdpvNΦPM。

(66)

式中：f为同步频率；kdpv为绕组系数，对所采用的绕组布线，该系数取0.933；N为每相串联匝数；ΦPM为永磁磁场所产生的每极磁通，且有

(67)

式中τp为极距。图5为解析法与FEM计算得出的相绕组空载反电动势结果对比，两者波形一致。

3.5 转矩

使用Maxwell应力计算转矩，转矩表达式为

(68)

在计算齿槽转矩时，式(68)中的磁场强度采用永磁体磁场结果。图6所示为一个齿槽转矩周期下的解析法和FEM结果对比，可见两者波形较为相符，解析解的幅值略高。齿槽转矩幅值约为0.000 4 N·m，为设计额定转矩(0.65 N·m)的0.06%，齿槽转矩非常小，可以忽略。从电机设计角度而言，永磁体与定子内径之间的半径间隙越大，永磁体磁场在定子内径处的径向、周向磁密越小，从而导致齿槽转矩减小。另外，当槽开口越窄，齿槽效应越弱，齿槽转矩也会减小。

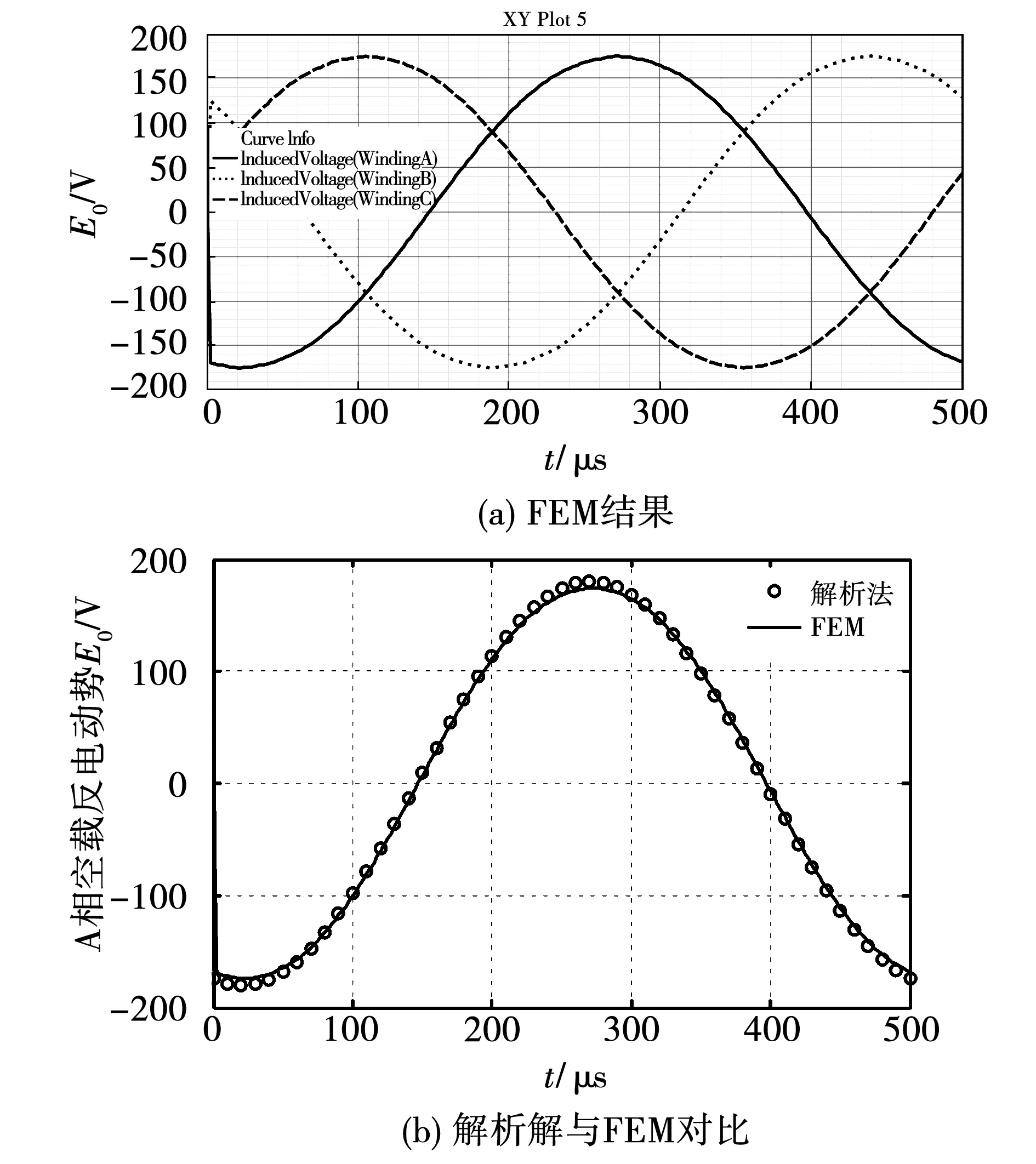
图5 相绕组空载反电动势Fig.5 EMF of open-circuit

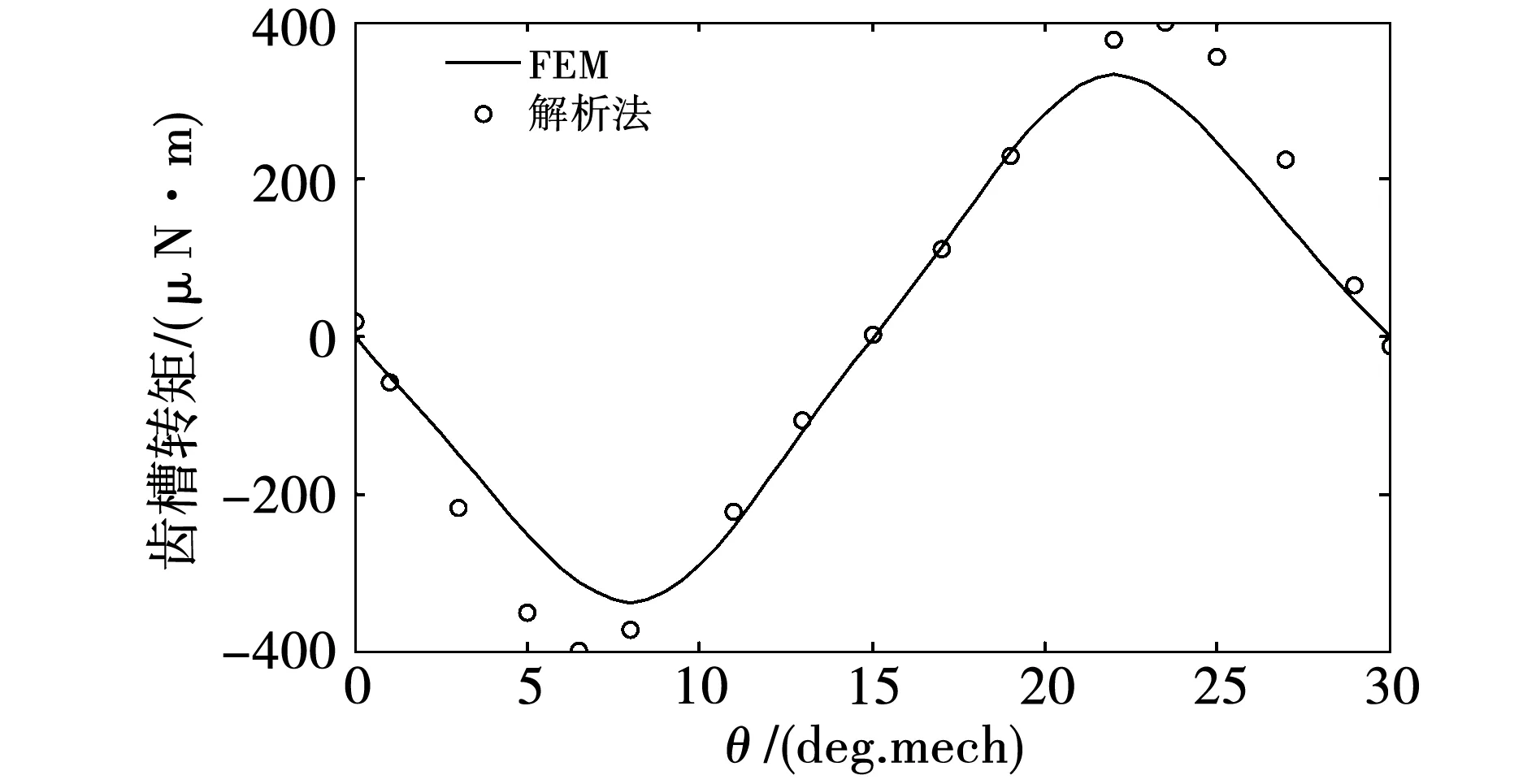
图6 齿槽转矩Fig.6 Cogging torque

在计算堵转转矩时，式(68)中的磁场强度采用负载磁场结果，只是永磁体的充磁方向固定不变，而电枢反应磁场以额定转速旋转。图7(a)显示了给定电流下堵转转矩的对比结果，解析解和FEM结果吻合，且获得的堵转转矩幅值为额定转矩的1.8倍，具有较好的过载能力。

在计算电磁转矩时，式(68)中的磁场强度采用负载磁场结果，永磁体的充磁方向和电枢反应磁场保持固定夹角，且均以额定转速旋转。图7(b)显示了给定电流下电磁转矩的对比结果，解析解和FEM结果吻合，解析解略高于FEM结果。电磁转矩的脉动幅值约为0.002 N·m，为额定转矩的0.30%，可以忽略。

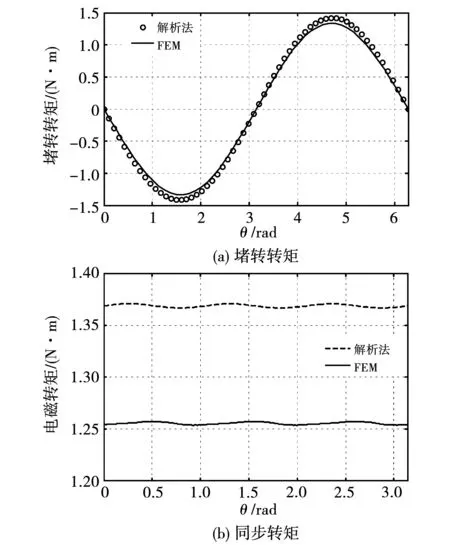
图7 电磁转矩Fig.7 Electromagnetic torque

4 高速永磁转子结构设计

超高速电机转子的设计需要兼顾励磁性能和动力学性能，一般采用两种结构，即方案A：“导磁芯轴+空心永磁体+纤维保护套”；方案B：“圆柱永磁体+合金保护套”，分别如图8(a)、(b)所示。

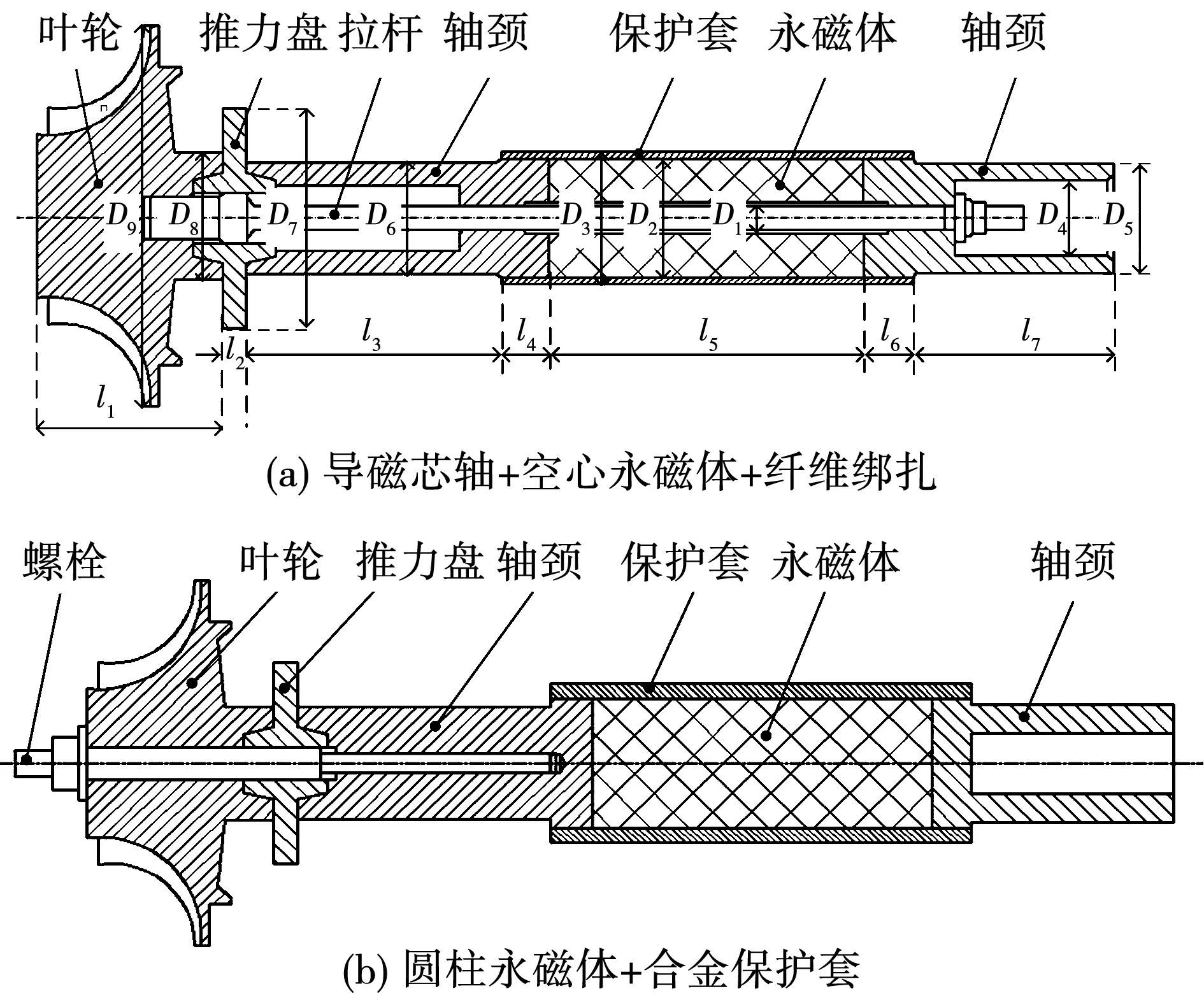
图8 两种结构转子Fig.8 Two types of rotors

如果采用表1所示的定子，具有相同励磁效果的两种转子磁钢段的尺寸以及其它附加结构的尺寸如表2所示，其中，两种转子的尺寸除了在磁钢段有差异外，其它尺寸都相等。在进行转子固有转速有限元计算时，由于纤维保护套和永磁体的抗弯刚度相对于合金钢轴非常小，可以作为附加质量处理。转子各个部件的材料属性见表3。

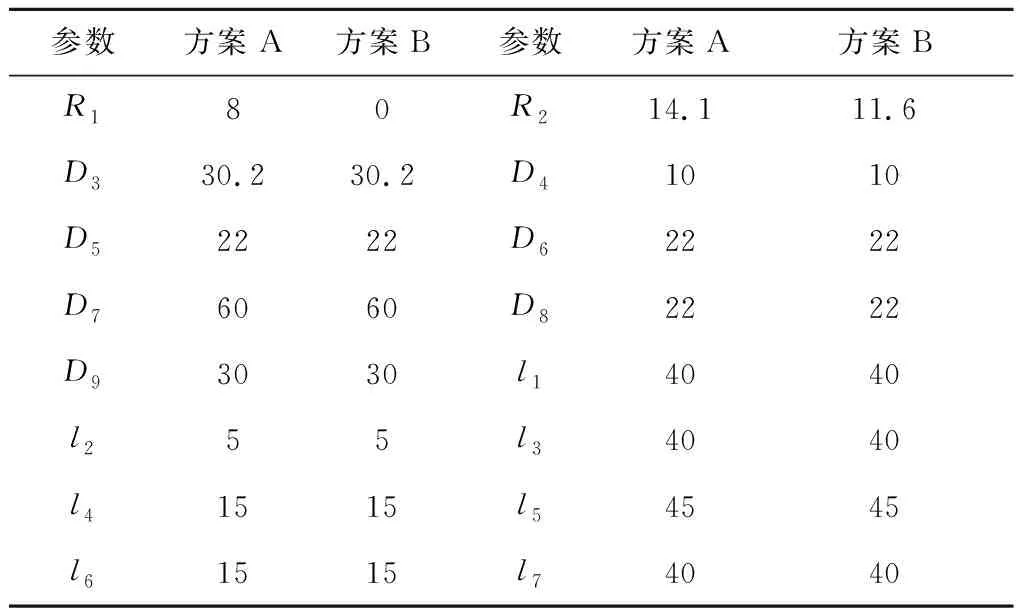
表2 两种转子参数

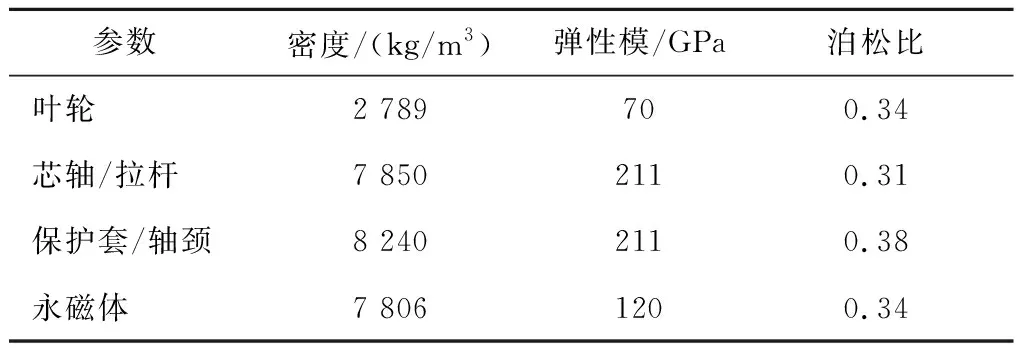
表3 转子材料属性

图9给出了两种转子的固有频率。方案A转子的一阶、二阶弯曲固有频率分别为1 014 Hz和2 003 Hz；方案B转子的一阶、二阶弯曲固有频率分别为2 394 Hz和5 412 Hz。

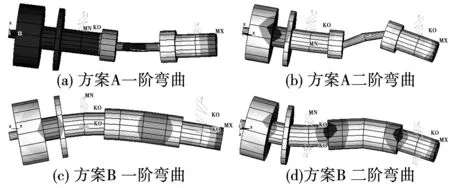
图9 两种结构转子固有频率Fig.9 Natural frequencies of two types of rotors

以上计算表明：如果需要转子在工频2 000 Hz时为刚性转子，方案A不可行，而方案B满足要求。依靠增加芯轴的直径来获得更高的临界转速的效果并不特别明显，反而造成永磁体外径膨胀，占据过多的气隙空间。对于方案B，虽然合金保护套厚一些，但是永磁体的外径小，在留有相同气隙厚度时，可以获得更高的固有转速。

5 结 论

本文针对装配极弧数为1的平行充磁两极转子的超高速PMSM，建立了电机的精确子区域解析模型，适用单层、双层叠绕绕组结构；考虑了定子槽和定子齿尖效应，可计算开路磁场、电枢反应磁场和负载磁场，进而可计算空载反电动势、齿槽转矩和电磁转矩，并用FEM验证了该解析方法的准确性。设计了“圆柱永磁体+合金保护套”和“导磁芯轴+空心永磁体+纤维绑扎”两种结构转子，并进行临界转速的对比。结果表明，在提供相同励磁磁场时，“圆柱永磁体+合金保护套”转子更有益于达到超高速。本文的研究为超高速电机的设计和优化提供了理论参考。