基于深度强化学习的水空跨域机器人水面起飞运动控制

2021-02-22霍雨佳李一平封锡盛

电机与控制学报 2021年12期

霍雨佳，李一平，封锡盛

(1.中国科学院沈阳自动化研究所机器人学国家重点实验室，沈阳 110016；2.中国科学院机器人与智能制造创新研究院，沈阳 110169；3.辽宁省水下机器人重点实验室，沈阳 110169；4.中国科学院大学，北京 100049)

0 引言

近年来，随着无人机和水下机器人技术的迅速发展，水空跨域机器人因其兼具了水下航行的高隐蔽性和空中飞行的高机动性，逐渐成为新的研究热点[1]。

水空跨域海洋机器人，也称水空两栖跨介质机器人，一般指可在空气中和水下(或水面)均具备作业能力的机器人；本文中特指具备在水空两栖作业能力和在水空间反复、多次跨域能力的机器人。根据跨域机器人的跨域方式不同，通常可分为直接跨域式和分步跨域式[2]。直接跨域方式指机器人以俯冲或滑行方式在水面降落入水，以通过气体或液体喷射获取初始动能方式脱离水面[3]。这种方式多由固定翼构型机器人采用，对机器人的结构设计和运动控制提出了较大的挑战，同时喷射气体出水方式限制了机器人多次跨域作业的能力。分步跨域式指机器人以旋翼构型机器人方式实现在水面进行起飞和降落，以通过浮力调节等方式在水面实现水空间的跨域作业，并利用旋翼提供升力。这种方式可由固定翼构型机器人[4-6]和旋翼构型机器人[2,7-10]采用，相较于旋翼构型，固定翼构型因具备更优的空中飞行效率和飞行速度等优势而多被采用。

水空跨域机器人需要在多种环境下进行作业，其不规则外形在不同介质下的受力具有高度的复杂性，特别是机器人在跨域过程中，水空分界面受到外界环境下风、波浪和机器人螺旋桨推进器吹出的气、水干扰，使得机器人在当前环境下的动力学特性具有极大的不确定性，难以使用传统的方法对机器人在空气和水中的动力学模型进行精确构建。现阶段，世界范围内对跨域机器人的研究尚处于初始探索阶段，跨域机器人多采用与旋翼无人机相似的PD/PID控制器实现机器人的自主跨域过程，且均部署于小型机器人，不适用于大型跨域机器人。

近年来，人工智能技术的发展，为机器人提供了新的选择方案。强化学习作为一种无模型方法，无需对机器人控制系统建立模型，而是通过机器人与环境的交互，可以在动态环境中逐步习得有效的控制策略，并不断对现有控制策略进行优化。这种方法为水空跨域机器人的运动控制，特别是跨域过程的运动控制提供新的思路。目前，强化学习方法在空中和水下机器人的运动控制均有着不同程度的应用[11]，Hwangbo等[12]利用确定性策略搜索方法实现了四旋翼无人机空中三维位置的跟踪。Koch[13]利用ROS和Gazebo仿真软件，分别运用DDPG、TRPO和PPO三种深度强化学习算法实现对Iris四旋翼机器人的姿态控制，并与充分调参的PID控制器进行对比，获得了更好的控制效果。Song等[14]利用PPO算法实现了四旋翼无人机的竞速任务。

然而，一般的旋翼机器人的强化学习运动控制方法，未考虑大型跨域机器人在近水面的螺旋桨高转速下的推力损失等问题，很难直接应用于大型跨域机器人的跨域过程。

本文提出一种基于强化学习的跨域机器人出水过程的控制策略方法。为了准确描述跨域机器人跨域过程中的动力学特性，通过实验和计算获得螺旋桨推进器近水面的动力学特性和机器人跨域过程中的浮力变化。最后，对机器人的跨域出水过程进行仿真和试验，验证基于强化学习的跨域机器人水面起飞控制的有效性。

1 跨域机器人近水面模型

本文采用水空跨域海洋机器人主体部分为鱼雷型回转体，搭配四台可倾转180°的水空两用螺旋桨推进器和两具可折叠机翼，如图1所示。

图1 水空跨域机器人结构示意图Fig.1 Aquatic-aerial trans-domain robot

该机器人布局借鉴自倾转四旋翼机器人，由文献[15]可知，定义载体坐标系原点与机器人重心G重合，令Ω={p,q,r}T表示载体坐标系下机器人在横滚、俯仰和偏航方向角速度；Φ={φ,θ,ψ}T表示机器人姿态角；U={u,v,w}T为载体坐标下机器人各方向线速度；PW={x,y,z}T为世界坐标系下机器人位置。则跨域机器人的动力学模型可描述为：

(1)

其中：FB={Fx,Fy,Fz}T表示载体坐标系下机器人各方向分力；MB={Mx,My,Mz}T为载体坐标系下机器人绕各轴力矩；RB→W为载体系到世界坐标系的旋转矩阵；JB→W为载体角速度到姿态角速率间的旋转矩阵；机器人的质量m和转动惯量矩阵I可由测量可得。

机器人在近水面的受力主要来自于倾转推进器的推力FT、重力G、机器人在水面以下部分受到的浮力B以及流体力FD。则世界坐标系下，机器人的受力可描述为：

(2)

其中：FT,i、MT,i、FD,i、MD,i(i=x,y,z)分别表示螺旋桨推进器产生的力和力矩、机器人在介质中运动产生的流体力和力矩在世界坐标系下的各轴分量；MB,i(i=x,y,z)分别表示机器人在近水面运动时浮力产生力矩在各轴的分量。

1.1 倾转螺旋桨推进器模型

理论上，当流速度较小时，单个螺旋桨推进器的推力、转矩与转速相关，可描述为：

T=kTω2；

(3)

τ=kτω2。

(4)

其中：kT为螺旋桨拉力系数；kτ为螺旋桨力矩系数。

水空跨域海洋机器人采用水空两用桨提供动力，螺旋桨在水中与空中采用两套电动机在不同转速下工作。机器人水面起飞采用空中电机带动螺旋桨工作，由于空气中螺旋桨高转速使水面产生较大扰动和较大水汽，此时螺旋桨近水面模型与空气中模型不同，如图2所示。

图2 螺旋桨近水面工作示意图Fig.2 Propeller water-surface operation

由实验可知，螺旋桨在近水面的推力相较于空气中有着不同程度的减弱，这种推力减弱同螺旋桨桨叶距水面距离hs相关，如图 3所示。

图3 螺旋桨在近水面和空气中推力对比Fig.3 Propeller force in condition of air-water surface and air

假设螺旋桨在近水面的推力模型依旧满足式(3)，可得螺旋桨模型更改为

T=kv(h)kTω2。

(5)

其中：kv(h)描述了不同离水面距离h情况下，螺旋桨的衰减系数，表示了离水面距离h时，当前螺旋桨力T(ω,h)模型和空气中螺旋桨力Tair(ω)的比值，表示为

(6)

对于不同离水面距离h情况下，螺旋桨的衰减系数kv(h)的模型由节2.1进行模型回归。

同时，机器人单个倾转推进器的力和力矩可描述为：

(7)

Mr,j=FT,j×Lj。

(8)

其中，j=1,2,3,4，分别表示4台倾转推进器。δj表示第j个推进器的倾转角度。Lj表示第j个推旋翼进器中心距离重心G的距离，则Lj为

(9)

其中：dx,i为第i个倾转旋翼推进器轴中心到机体坐标系下xGz平面的距离；dy,i为倾转旋翼推进器轴中心到机体坐标系yGz平面的距离；hT为推进器旋翼中心到倾转轴的距离。

1.2 机器人近水面浮力模型

由于深度和姿态变化，机器人在水面受到浮力大小与作用位置也因此发生改变，如图4所示。其中：G为机器人所受到的重力；B为机器人所受到的浮力，这部分浮力由机器人位于水面下的部分排开水所产生并作用于当前的浮心。假设机器人当前的浮心载体坐标系下坐标为{xb,yb,zb},则浮力产生的力矩为

MB,x=Bcosθ(zBsinφ-yBcosφ)，

MB,y=B(xBcosφcosθ+zBsinθ)，

MB,z=B(xBsinφcosθ+yBsinθ)。

图4 跨域机器人浮力示意图Fig.4 Buoyant schematic of trans-domain robot

2 跨域机器人近水面模型回归

为获得仿真所需的机器人近水面的动力学模型，需要分别获取近水面环境下螺旋桨的推力模型和机器人不同深度、姿态情况下的动力学模型。

2.1 近水面螺旋桨推力模型回归

由1.1可知，螺旋桨在近水面环境下工作时，其推力受到不同程度的影响，这种影响主要由螺旋桨桨叶与水面的距离决定。

由于难以对kv(hs)进行参数化建模，考虑采用非参数化建模方法，即高斯过程回归方法，实现对kv(hs)进行建模[16-17]。

kv(hs,i)=f(hs,i)+εi，i=1,2,…,n。

(10)

kv～N(μ,Kn)。

(11)

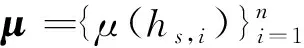
此时，该模型的联合高斯分布函数可描述为

p(kv|hs)=

(12)

则f(hs*)的条件分布服从新的分布：

(13)

此时，后验均值和方差可描述为：

μ*=μ(hs*)=

(14)

Σ.*=Σ(hs*)=K(hs*,hs)-

(15)

采用Matern核函数作为协方差矩阵，并对kv(hs)进行模型回归。

图5中描述了螺旋桨动力衰减系数对不同的叶片距水距离关系的高斯过程回归。点状为实际测量的kv值，灰色区域为模型预测值的95%置信区间，拟合曲线为基于高斯过程回归获得的螺旋桨衰减系数模型的预测值。

图5 螺旋桨动力衰减系数和其高斯过程回归Fig.5 Propeller power attenuation kv(h) and GP regression

基于上述模型，可以获得不同叶片离水面高度的kv系数，相应地获得了螺旋桨在近水面不同高度下的力和转速模型。

2.2 近水面浮力估算模型

由于机器人的排水体积主要由其AUV形主体提供，为方便计算机器人不同深度、姿态下的排水体积和浮心位置，将机器人主体假定为圆柱。根据机器人的深度和姿态(俯仰角θ)，其排水状态可分为4种，如图6所示。点A和B为载体坐标系下本体的端点，EF和CD为本体在载体坐标系下平面O-XZ的上下端线。

图6 机器人与水面相交情况示意Fig.6 Schematic of water surface and robot

由此，通过获取机器人排水体积和浮心位置可由上述情况中的入水深度和姿态，即各点坐标计算得到。通常的，机器人的入水深度由深度传感器获取，其在机器人本体下后部平面CDEF上，载体坐标系下PD(xD,0,zD)，而在简化模型中，机器人的横滚角φ只影响深度传感器的数据，不影响机器人的排水体积。故定义水面坐标系O-XGYGZG，原点O为AB与水面交点，XG为OX与水面交线，ZG过点O与水边垂直。当深度传感器测量值为d，姿态角Φ={φ,θ,ψ}T时，则水面坐标系和载体坐标系之间关系为

(16)

其中：

TB→S=

为不失一般性，考虑情况2，计算NMDF的体积和形心，如图7，其体积可分割为NMN′和NN′DF，NMN′可由下式对弓形GPG′的面积进行积分[18]

(17)

其形心为：

(18)

其中，S0(z)和S1(z)表示弧GPG′为劣弧和优弧，即z<0和z≥0时的截面积。当前弓形截面积S(z)可描述如下：

(19)

(20)

(21)

图7 排水体积计算示意图Fig.7 Schematic of displacement volume computing

其中：R为机器人本体半径；Z=zM=-zN=Rtanθ。则NMN′的体积和形心为：

(22)

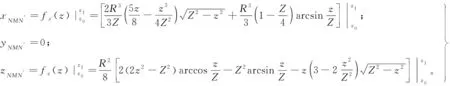
(23)

相应地，根据式(22)和式(23)计算不同情况下机器人的排水体积和浮心。如图6中，对于情况1：z0=zN，z1=zA，而圆柱体FNN′D的体积VFNN′D=πR2(zN-zB)，则总的排水体积V=VNMN′+VFNN'D，浮心为

(24)

同理，对于情况2：z0=zN，z1=zM，排水体积V=VNMN′+VFNN′D；情况3：z0=zB，z1=zA；情况4：z0=zB，z1=zM。

为验证排水体积估算的有效性，对比不同深度和姿态下的排水体积和浮心的实际值和估算值，如表1所示。考虑到机器人在起飞过程中，具有较小的横滚角，故仅考虑深度和俯仰的影响，并分别对跨域机器人采用SolidWorks软件测量(不包含推进器体积)和上述排水体积估算方法(不包含推进器体积)进行测量。

表1 排水体积估算对比

由表1可知，两种方法所得到的排水体积差值小于0.000 5 m3，满足对机器人本体排水体积的估算要求。

3 基于深度强化学习的跨域机器人水面起飞控制

考虑到水空跨域机器人在近水面起飞过程中，水流等造成其水动力环境具有极高的不确定性，难以使用传统的水动力分析对其建立精确的环境模型。强化学习方法无需对环境建立精确模型，可在无先验知识情况下和复杂未知环境中具备较强的适应性。强化学习为机器人的水面起飞任务提供可行的控制方法。

3.1 跨域机器人水面起飞分阶段控制

为保证机器人在脱离水面过程中具备足够的动力，采用分阶段起飞控制方法，如图8所示。阶段①：机器人浮于水面上；阶段②：提高前桨(桨1、桨2)转速，使机器人具备一定的正仰角，减小螺旋桨距离水面过近造成的动力衰减，同时推进器发生倾转，保证动力竖直向下，避免机器人在此过程中产生较大的水平方向位移；阶段③：前桨距离水面大于500 mm，前桨获得足够动力，将机器人持续拉离水面，进而带动后桨脱离水面并具备无衰减动力。此时，机器人完全脱离水面，其4台螺旋桨均具备无衰减动力，跨域机器人转为空气中的倾转四旋翼机器人工作模式。

图8 跨域机器人分阶段水面起飞示意图Fig.8 Schematic of taking-off in stages

3.2 基于强化学习的水面起飞方法

目前，跨域机器人的水面起飞控制方法采用手动遥控控制，实验人员通过遥控器下达机器人x、y、z方向的线速度和r方向的航向角速度指令。强化学习方法实现对机器人收到的速度指令控制，同时依据需要，控制机器人达到一定俯仰角θ，并实现机器人横滚角不易过大(-15°≤φ≤15°)。

结合跨域机器人水面起飞的操作方法和3.1节所述的跨域机器人分阶段起飞方案，设计基于此任务的强化学习方法。

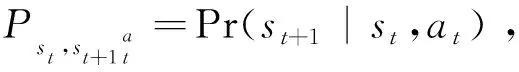
深度强化学习的目的是通过优化神经网络策略πθ的参数θ，使累计回报的最大化，则最优策略为

(25)

其中γ∈[0,1)为折扣因子。

为将跨域机器人的水面起飞任务同强化学习方法结合，实现机器人水面起飞控制，需要结合任务的实际需求，对状态s、动作a、奖励函数r和强化学习训练的初始和终止状态进行适当选取，这些变量的合适选取和设计，可改善强化学习的训练效果和机器人的控制性能。

1)状态s的选取。

对于跨域机器人的水面起飞控制，定义观测状态st=[Ut,Φt,Ωt,d]。此刻，姿态角信息Φt=[φt,θt]，只考虑机器人的横滚角和俯仰角，不考虑机器人的航向角。

2)动作a的选取。

一般情况下，当机器人进行螺旋桨无动力衰减情况下水面起飞，选取机器人的4台螺旋桨转速[ω1，ω2,ω3,ω4]和4部推进器的倾转舵机的倾转角度[δ1,δ2,δ3,δ4]。由于机器人的螺旋桨转速和倾转舵机的角度难以实施短时间内较大的动作量变化，定义动作变化量阈值Δωth和Δδth，则下一时刻动作应有ωt+1∈[ω-Δωth,ω+Δωth]和δt+1∈[δ-Δδth,δ+Δδth]。

3)奖励函数r的构造。

对于跨域机器人水面起飞任务，目标指令由遥控器得到[utarget,vtarget,wtarget,rtarget]。通常地，在水面起飞过程中，取[Utarget,rtarget]=[0,0,wtarget,0]。

当机器人未完全脱离水面，需保证机器人具备一定的正仰角θ。同时，不考虑航向角ψ，只考虑机器人具备接近于0的航向角速度r。即目标姿态角Φtarget=[φtarget,θtarget]=[0，θtarget]，和目标角速度Φtarget=[ptarget,qtarget,rtarget]=[0,0,0]。

则即时奖励函数为

(26)

其中，前三项分别描述机器人在线速度、姿态角、角速度与目标值的差值，最后一项描述了机器人是否在水中，如果机器人处于空气中，深度d<0，则最后一项不产生惩罚值。

4)初始、终止的选取。

强化学习通过反复地与环境进行交互，以获取最优的控制策略，其初始状态为机器人处于水面某点，并处于平衡状态s0=[0,0,0,0,0,0,0,0,d0],d0为机器人漂浮于水面深度传感器测量值。

机器人在强化学习算法中，其每回合试验都应到达一终止状态，当到达该状态后，本回合试验结束。因此为节约训练成本，有必要设置终止条件，当机器人完全离开水面并维持超过5 s，则认为本次试验成功，回合结束。同时，为防止机器人过长时间到达不了终止状态，设置最大试验时间，t≤Tth。

5)强化学习方法的运用。

本文采用近似策略优化(proximal policy optimization, PPO)[19]算法对机器人的水面起飞控制进行训练，如图9所示。

图9 机器人强化学习控制框图Fig.9 Reinforcement learning control block diagram of the robot

由图9可见，深度强化学习控制器获取目标状态starget和当前机器人状态sk(或初始状态s0)，由此计算出相应的机器人动作ak，并发布到机器人的执行机构作出相应的动作，通过传感器获得机器人下一时刻的状态sk+1，并判断是否达到终止状态，若没有，则将状态sk+1传递至强化学习控制器，进行下一时刻的动作量ak+1计算，否则，结束当前训练。同时，通过对每一时刻机器人状态、动作和奖励构成的元组〈sk,ak,sk+1,rk〉的存储，并采用PPO算法实现对深度强化学习控制器的更新，实现对机器人控制器的训练。

对于跨域机器人的水面起飞任务，这种高维状态和动作空间的过驱动控制问题，依旧为PPO算法提出了挑战。为简化PPO算法寻优的复杂度，采用将起飞任务分解训练的方法。

对于机器人的训练来说，最初的训练不能顺利地完成整个水面起飞任务流程，这往往导致机器人反复训练最初的几个动作，而忽略了后面的动作。通过将水面起飞动作进行分解，则得到3组需要训练的动作流程，其将3.1节所述的3步起飞流程对应3组训练：动作①：控制桨1、2的转速，使机器人从水平初始状态到具备一定正仰角，此时桨3、4处于低速状态，4台倾转舵机随机器人转动，保证推力竖直向下；动作②：机器人部分浸没于水中，控制桨1、2的转速，使机器人以固定的仰角实现将机器人逐渐拉离水面，此时桨3、4处于低速状态，4台倾转舵机随机器人转动，保证推力竖直向下；动作③：机器人完全脱离水面，控制4具螺旋桨的转速和4台倾转舵机的角度，使机器人4台螺旋桨均脱离近水面状态。

4 仿真与试验

4.1 基于ROS和Gazebo机器人水面起飞仿真

为验证跨域机器人水面起飞方案和强化学习控制算法的有效性，基于ROS和Gazebo仿真软件，搭建跨域机器人的仿真平台。并在此基础上强化学习算法通过ROS与Gazebo进行动作命令的发布和状态信息的订阅。

由图10所示，深度强化学习采用包含2个全连接隐含层的网络结构，每层128节点，激活函数采用tanh。学习率l=10-4，折扣因子γ=0.99，GAE参数λ=0.95，截断参数ε=0.2，采样频率20 Hz。

图10 深度强化学习网络结构Fig.10 Network architecture of DRL

采用3.1和3.2节所述方法，对机器人在近水面环境下进行仿真。仿真中，机器人初始位置位于水面某处，通过遥控器给定目标值[u=0,v=0,w=1.5 m/s,r=0]，机器人t=0 s时开始动作。

机器人在t=0 s到t=3.6 s，处于阶段①，机器人桨1、2开始动作(图12)，此时机器人获得抬艏力矩，使机器人获得30°的正仰角。

图11 螺旋桨动力衰减情况下机器人水面分阶段起飞仿真Fig.11 Simulation robot water-surface taking-off in stages with propeller power attenuation

图12 机器人水面起飞螺旋桨转速Fig.12 Propeller rotation action of water-surface taking-off simulation

机器人在t=3.6 s到t=5.7 s，处于阶段②，桨3、4脱离水面并开始动作。机器人逐渐获得最大65°的仰角。在此过程中，由于桨3、4开始提供升力，桨1、2的所需的转速开始减小。

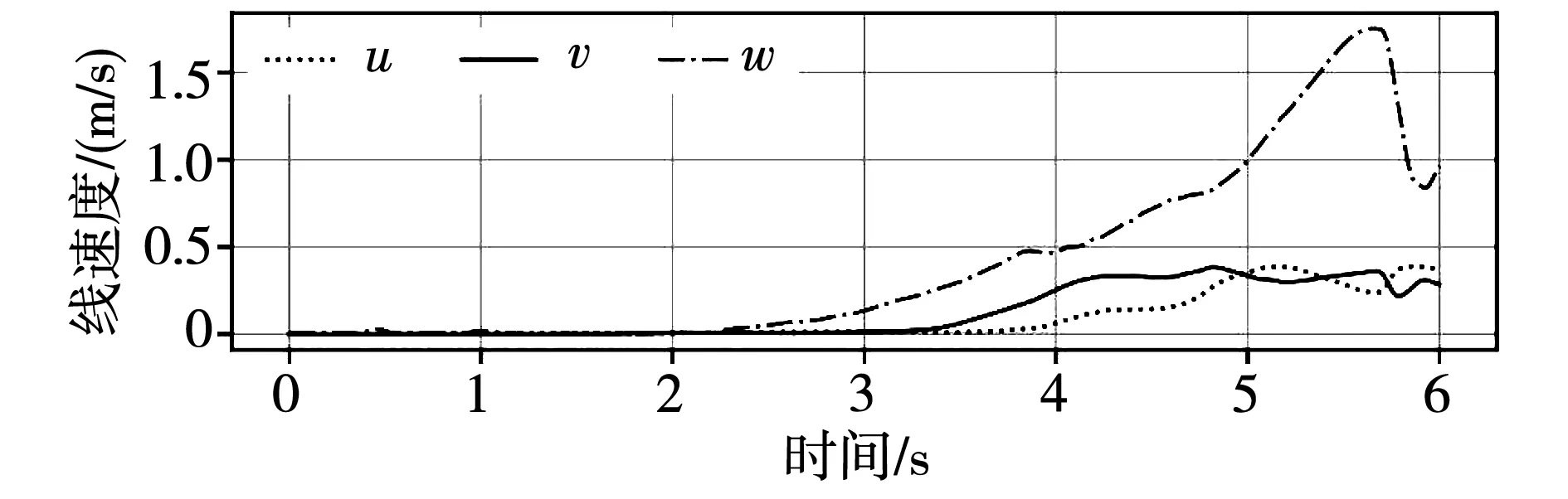
图14 机器人水面起飞线速度Fig.14 Linear velocities of water-surface taking-off simulation

机器人在t=5.7 s到t=6 s，处于阶段③，机器人到达距水面高度2 m位置，完全脱离近水面状态，4台倾转舵机逐渐恢复90°。在此过程中，机器人逐渐由大仰角状态恢复到水平状态，桨1、2适当减小转速，桨3、4增大转速，为机器人提供俯仰力矩，保证机器人逐渐恢复水平。

图15 机器人水面起飞姿态角Fig.15 Attitude of water-surface taking-off simulation

由仿真可知，基于强化学习的机器人达到目标速度w=1.5 m/s,水平线速度小于0.5 m/s，同时，机器人以60°的仰角实现由水到空气的水面起飞。仿真证明了螺旋桨动力衰减情况下，基于深度强化学习的机器人水面分阶段起飞的有效性和可行性。为下一步实际机器人的实验验证提供保证。

图16 机器人水面起飞深度(高度)Fig.16 Depth(height) of water-surface taking-off simulation

4.2 机器人水面起飞实验验证

为缩短机器人运动控制的强化学习训练时间，节约机器人的训练成本，通常机器人应提前在虚拟环境中进行仿真训练，得到较好的训练效果后，将训练所得的网络部署于实体机器人中，并将该网络作为实体机器人运动控制的初始化网络。

机器人控制模块主要由PX4控制板和Jetson TX-2深度学习计算模组构成，如图17所示，PX4主要承担通讯和数据记录功能，并与无线遥控器实现通讯并下发指令；前述仿真训练所得网络部署于TX-2中，通过向PX4获取当前机器人的运动状态和遥控发出的控制指令，计算下一步机器人的控制策略；机器人通过外接的60V直流电源通电。

图17 实验平台构成Fig.17 Elements of experimental test

实验验证包括2组飞行实验，第1组为无螺旋桨衰减情况下的水面起飞实验，第2组为螺旋桨动力衰减情况下的水面起飞实验。

4.2.1 无螺旋桨衰减情况下水面起飞

为验证机器人在无螺旋桨衰减情况下的水面起飞控制效果，考虑在机器人水面起飞环境中剔除螺旋桨近水面动力衰减的因素。该组实验中，制作一组铝合金框架，4台倾转推进器沿机体坐标系-Gz轴方向平移500 mm，由2.1节可知，此时螺旋桨的动力特性等同于空气中螺旋桨，此时4台推进器竖直向上，呈固定的90°布置，如图18所示。

图18 螺旋桨无动力衰减情况下机器人水面起飞实验Fig.18 Robot water-surface taking-off without propeller power attenuation

机器人初始位置位于水面某处，通过遥控器给定目标值[u=0,v=0,w=2m/s,r=0]，机器人t=0 s时开始动作。

由于当前情况下，螺旋桨动力没有衰减效果，其4台螺旋桨提供的合力足够保证机器人以水平方式直接起飞。

由图19可知，四台螺旋桨转速控制在10 000到15 000 r/min，由此产生160 N的合升力。

图19 螺旋桨无动力衰减情况下机器人水面起飞螺旋桨转速Fig.19 Propeller rotation action of water-surface taking-off without propeller power attenuation

机器人在t=0 s到t=5 s保持上升状态，由图20可知，机器人在水面起飞过程中，维持水平线速度小于0.3 m/s，机器人获得的速度w较目标速度wtarget=2 m/s存在约1 m/s的差距，机器人垂向速度w在1 m/s到2 m/s之间振荡。这种垂直速度方向的振荡主要来自于机器人的外接电源线的拉扯，当机器人不断升高时，其也带动更多的电源线脱离地面，同时，地面上的电源线也在机器人的拉扯过程中同地面发生摩擦。电源线的重量和摩擦给机器人带来额外的向下的力，这种反复的拉扯一定程度上造成了机器人垂直方向速度w的振荡。

图20 螺旋桨无动力衰减情况下机器人水面起飞线速度Fig.20 Linear velocities of water-surface taking-off without propeller power attenuation

由图21可知，机器人在当前实验中，存在不超过5°的俯仰角和横滚角。但横滚角φ存在小幅振荡，尤其是起飞初始阶段，在t=0 s到t=2 s之间。这种现象主要来自于两种因素：一是此次实验中，将4台螺旋桨通过铝合金塑材架高了500 mm，这种结构使螺旋桨与搭载传感器的机器人本体之间仅靠铝合金框架连接，这种连接方式造成了机器人的振动；二是螺旋桨经过架高后，改变了机器人的重心，这种情况下的重心位于浮心之上，增大了机器人在水面的横滚。

图21 螺旋桨无动力衰减情况下机器人水面起飞姿态角Fig.21 Attitude of water-surface taking-off without propeller power attenuation

图22 螺旋桨无动力衰减情况下机器人水面起飞深度(高度)Fig.22 Depth(height) of water-surface taking-off without propeller power attenuation

由此实验可知，基于深度强化学习的机器人水面起飞方法，在当前机器人的布局下，可以满足跨域机器人以水平方式进行起飞。这种机器人的布局方式虽然仅是用于实验验证，不是跨域机器人的常规布局结构，但该实验通过排除了螺旋桨近水面动力衰减的影响，验证了深度强化学习方法在实际机器人中的有效性，为下一步实验提供了保证。

4.2.2 螺旋桨衰减情况下水面起飞

该组实验中，目的是实现机器人控制4台螺旋桨转速和4部推进器的倾转舵机的倾转角度，使机器人以倾转旋翼工作状态实现水面的分阶段起飞，如图23所示。