高增益准Z源网络间接矩阵变换器的结构研究

王固萍， 叶培乐， 王斌， 程启明， 薛育， 鲁飞

(1.国网上海市电力公司 经济技术研究院，上海 200122; 2.上海电力大学 自动化工程学院，上海 200090)

0 引 言

矩阵变换器由于具有高质量的正弦输入输出波形、可调输入功率因数、双向功率流和结构紧凑等优点而受到广泛关注[1-2]。传统的直接矩阵变换器(direct matrix converter，DMC)主要缺点是其控制和调制算法较为复杂，间接矩阵变换器(indirect matrix converter，IMC)较好地解决了这个问题。但是，直接或间接矩阵变换器都存在一个共同的问题，就是电压传输比最高仅为0.866。因此，为了提高电压传输比，很多研究都集中在矩阵变换器的拓扑结构和调制方式[3-5]。文献[6]采用了过调制的方法来提高电压传输比，但是由于存在输入电流和输出电压低次谐波，而且还需要加入LC滤波电路，导致实际成本增加。Z源网络是解决AC-AC、DC-AC和DC-DC变换器电压传输比受限的有效的方法。在文献[7-9]中，将准Z源(quasi Z-source, QZS)网络插入间接矩阵变换器中间，得到准Z源矩阵变换器(quasi Z-source matrix converter, QZS-MC)，可以使电压增益提高一倍以上，突破了传统矩阵变换器的电压增益的限制。许多研究都采用了不同的Z源拓扑结构和相关的控制方法，其目的是改变Z源变换器的运行状态，它们的原理相同[10-19]。文献[10]中将QZS-MC运用模糊逻辑控制应用于电机来进行造纸厂的流量控制，从而很好地控制造纸工艺中染料的流动。文献[11-12]将QZS-MC运用最优控制来调整调制系数与直通占空比之间的相互限制，找到最优的直通占空比。文献[13]用QZS-MC驱动感应电动机，利用粒子群优化算法来优化PI控制，设计旋转d-q电流控制方案。文献[14]将无源控制运用到QZS-MC，使得永磁同步电机能够稳定运行。文献[15]中改变QZS-MC的拓扑结构和调制技术，从而降低共模电压对电机的损害。文献[16]中介绍了QZS-MC的各种拓扑结构、电路分析、调制方案和应用。文献[17]中，将QZS-MC集成LC滤波器，通过小信号模型和电路分析，设计电压增益、滤波函数以及准Z源网络参数，仿真和实验验证了所建立的模型、电压增益分析和参数设计。文献[18]中，研究QZS-MC的两种调制方式，提出一种级联Z源网络的设计方法。文献[19]中将预测控制应用到QZS-MC模型中，来减少输出电压、电流的谐波分量。文献[20]中，将准Z源网络放置在间接矩阵变换器前面，它能够提供输入电压源连续电流的特性，还能增加矩阵变换器的电压增益，同时Z源网络作为输入滤波器进行工作，因此不需要额外的滤波电路。但是这些QZS-MC拓扑结构以及控制方法都存在相同的缺点，也即，为了提高电压增益，必须增加直通持续时间，从而需要降低调制系数，但这将导致输出电压的质量恶化，因此在实际应用中，电压增益一般不超过3～4倍。

为了解决上述问题，本文提出了一种在一定电压增益下会有较小的直通占空比的新型矩阵变换器。它的拓扑采用两个准Z源网络和间接矩阵变换器相结合，从而得到双准Z源矩阵变换器(two QZS-MC，TQZS-MC)。其调制算法的思想是两个准Z源网络之间配合升高电压，明确直通占空比，从而在不降低输入输出波形质量的前提下，获得更高的电压增益。实验结果表明该结构不仅存在升高电压能力，且降低了输出电流总谐波率 (total harmonic distortion, THD)。

1 间接矩阵变换器和Z源间接矩阵变换器存在问题

1.1 间接矩阵变换器存在问题

间接矩阵变换器是由整流级和逆变级构成的两级变换电路，可以实现调节输入功率因数，逆变级调制系数不需要修正，整流级可以实现零电流换流，以及不需要复杂的四步换流等优点。矩阵变换器输出电压与输入电压满足关系

(1)

式中：uin为三相电源输入电压；uout为矩阵变换器输出电压；mi、mo分别为整流级、逆变级的调制系数。

若式(1)中mi=mo=1，则

(2)

1.2 单Z源间接矩阵变换器的存在问题

单Z源间接矩阵变换器是由准Z源结构与间接矩阵变换器构成，因为Z源网络能够提高电压能力，克服了矩阵变换器存在最高电压增益仅为0.866的问题。

单Z源间接矩阵变换器输出电压与输入电压关系为

(3)

式中B为升压因子，其满足

B=1/(1-2D)。

(4)

式中D为直通占空比。理论上当D接近0.5时，升压因子B会趋向于无穷大，但是，直通占空比D与调制系数m存在限制关系，其关系式为

D+m≤1。

(5)

上式表明D与m之和不大于1。当改变直通占空比D，提高电压增益时，调制系数m要减小，由式(3)可知，实际电压增益会小于理论值。因此，存在的问题为直通占空比D与调制系数m的限制关系会导致电压增益不会超过3～4倍。

2 双Z源间接矩阵变换器的原理

2.1 拓扑结构

图1为双Z源间接矩阵变换器拓扑结构。由图可见，它是由两个准Z源网络和间接矩阵变换器所构成。图中，第1级为连续型准Z源网络，放在间接矩阵变换器的前面；第2级准Z源网络放在间接矩阵变换器的中间。这种结构能够使得三相输出电压增益远大于传统Z源矩阵变换器。

图1 双Z源间接矩阵变换器的拓扑Fig.1 Topology of two Z-source indirect matrix converter

2.2 双Z源间接矩阵变换器的升压原理

对双Z源间接矩阵变换器电路进行分析时，可单独分析整流级Z源网络和逆变级Z源网络。

2.2.1 整流级Z源网络

对于整流级网络，将逆变级Z源网络等效为二端口网络。

图2为双Z源间接矩阵变换器的整流级等效电路。由于拓扑结构为对称结构，所以设每一相电感和电容满足下面关系：

(6)

当电路工作在非直通状态时，开关Sx(x=a,b,c)导通，其等效电路见图2(a)。下面以a相为例推导升压原理。此时有：

(7)

当电路工作在直通状态时，开关Sx关断，其等效电路见图2(b)。下面同样以a相为例，此时满足：

(8)

由伏秒平衡原理可知，在一个开关周期Ts内，Z源电感两端的平均电压为0，结合式(7)、式(8)可得：

(9)

式中Drec为系统工作时整流级直通占空比。

由式(4)可得

(10)

即整流级的升压因子Brec为

(11)

图2 双Z源间接矩阵变换器的整流级等效电路Fig.2 Rectifier equivalent circuit of two Z-source matrix converter

2.2.2 逆变级Z源网络

对于逆变级网络，相当于一个Z源逆变器。其等效电路如图3所示。

当等效电路工作在非直通状态时，二极管导通如图3(a)所示。此时满足：

(12)

式中：uL1、uL2和uC1、uC2分别为电感L1、L2和电容C1、C2两端电压；UDC为虚拟直流级输入电压；UDC1为虚拟直流级输出电压。

当等效电路在直通状态时，二极管关断如图3(b)所示。此时有：

(13)

与整流级网络升压原理一样，由式(12)、式(13)可推出逆变级的升压因子Binv为：

(14)

UDC1=BinvUDC。

(15)

式中Dinv为系统工作时逆变级直通占空比。

图3 双Z源间接矩阵变换器的逆变级等效电路Fig.3 Inverter equivalent circuit of two Z-source matrix converter

2.2.3 双Z源间接矩阵变换器的升压能力

根据虚拟整流器输入输出功率守恒，有

(16)

从而可得

(17)

其中

(18)

(19)

式中uin为三相输入电压ua、ub、uc。

对于逆变级而言，其中

(20)

式中：mo为逆变级调制系数；uout为逆变级输出电压uA、uB、uC。由式(15)、式(19)推出下面关系：

(21)

B=BrecBinv。

(22)

式中B为双Z源间接矩阵变换器(TQZS-MC)的升压因子。

在理论上，式(21)表明了双准Z源间接矩阵变换器能够提高输出电压。

3 双Z源间接矩阵变换器的调制策略

该拓扑采用双空间矢量调制策略，且整流级、逆变级都采用有零矢量的空间矢量调制。

在整流级中，6个双向开关可分成两类空间矢量，输入电流有效矢量(I1～I6)和零矢量，其中零矢量又可以细分为直通零矢量和非直通零矢量，如图4所示。图中，括号内的数字按顺序代表a、b、c三相桥臂上、下开关的通断状态，其中：“1”代表上桥臂开关导通而下桥臂开关关断；“0”表示上下桥臂都关断；“-1”表示下桥臂开关导通而上桥臂开关关断。

图4 整流级输入电流空间矢量分布图Fig.4 Space vector diagram of front-end rectifier stage

逆变级同样存在6个开关合成6个输出线电压有效空间矢量(V1～V6)、直通零矢量和非直通零矢量。如图5所示，括号里面数字代表上、下功率开关的通断状态，其中“1”为上桥臂导通，“0”为下桥臂导通。

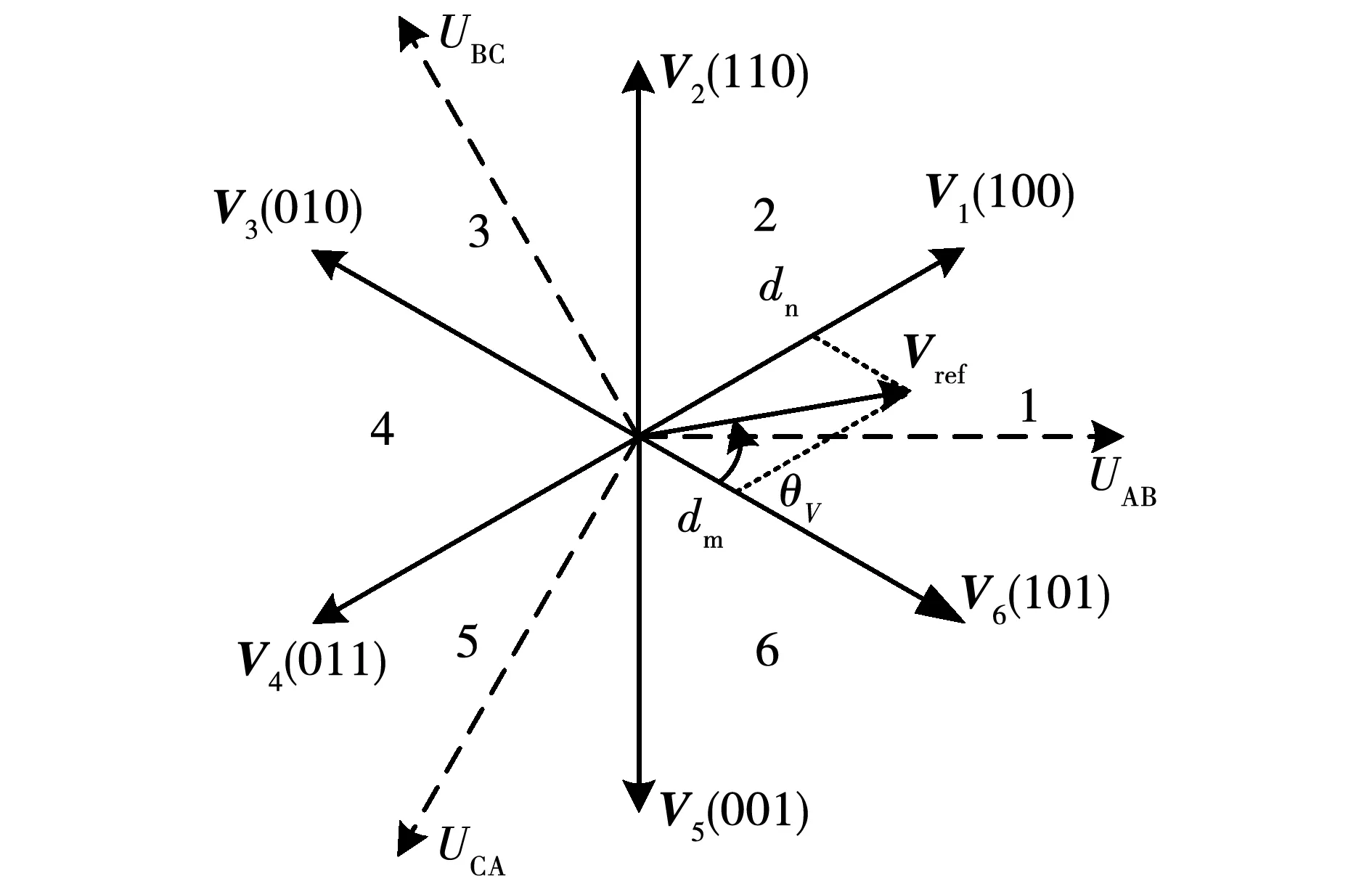
图5 逆变级输出电压空间矢量分布图Fig.5 Space vector diagram of back-end inverter stage

3.1 整流级调制

整流级调制是基于输入电流参考矢量。其中整流级存在11种开关状态见表1。

表1 整流级开关状态

假设输入电流参考矢量Iref在第1扇区，与第1扇区相近的两个有效矢量I1和I6合成，如图4所示。设dα、dβ、d0.rec、dst.rec分别为整流级矢量I6、I1、I0、Id的占空比，则有

Iref=dαI6+dβI1。

(23)

其中相应占空比满足[13]：

(24)

将所有零矢量全部作为直通零矢量，也可以满足增压控制，从而使占空比变为：

(25)

式中：θi为输入电流矢量角；mi为输入电流矢量调制系数，它满足0≤mi≤1。

3.2 逆变级调制

逆变级调制是基于电压参考矢量。逆变级有6个有效矢量、两个非直通零矢量以及3个直通零矢量，所对应的开关状态见表2。

表2 逆变级开关状态

采用简单升压策略实现整流级的零电流换流。假设参考输入线电压Vref在第1扇区，相邻两个有效空间矢量为V1和V6，Vref可由矢量V1和V6合成，如图5所示，其表达式为

Vref=dmV6+dnV1。

(26)

相邻电压有效矢量占空比计算为：

(27)

式中：θV为输出电压矢量角；mo为输出电压矢量调制系数，它满足0≤mo≤1；dm、dn、d0.inv、dst.inv分别为逆变级矢量V6、V1、V0、Vd的占空比。

将整流级直通占空比dst.rec按照式(13)表示，进一步推导可得

(28)

其中θi满足0≤θi≤π/3，那么dst.rec应满足

(29)

若设定mi=mo=0.8，Dinv=0.1，则dst.rec取值范围为0.2≤dst.rec≤0.3。那么整流级升压因子Brec应满足1.67≤Brec≤2.5，则B应满足2.087 5≤B≤3.125，这远大于单Z源矩阵变换器升压因子。

3.3 开关序列组合

因为每个开关周期内的平均输入和输出功率相等，并且输入和输出的开关模式之间需要精确的协调。因此整流级和逆变级的切换不能独立完成，必须计算开关模式的精确组合，来分配停留的时间和开关动作顺序。相应的开关序列占空比可以通过以下方式计算：

(30)

式中：dαm、dαn、dαst.inv、dα0.inv、dβm、dβn、dβst.inv和dβ0.inv为一个开关周期内不同输出电压矢量的占空比。其中电压矢量占空比要满足

dαm+dαn+dαst.inv+dα0.inv+dβm+dβn+dβst.inv+dβ0.inv=1。

(31)

对于整流级，开关组合为Ist-Iα-Ist-Ist-Iβ-Ist，因此，每一个Ist所对应dst.rec/4，Iα、Iβ对应占空比dα、dβ；对于逆变级，开关组合为V0-Vst-Vm-Vst-Vn-Vst-V0-V0-Vst-Vn-Vst-Vm-Vst-V0，V0对应占空比分别为dα0.inv/2、dβ0.inv/2,Vst对应占空比分别为dαst.inv/3、dβst.inv/3，Vm对应占空比分别为dαm、dβm,Vn对应占空比分别为dαn、dβn。如图6 所示。

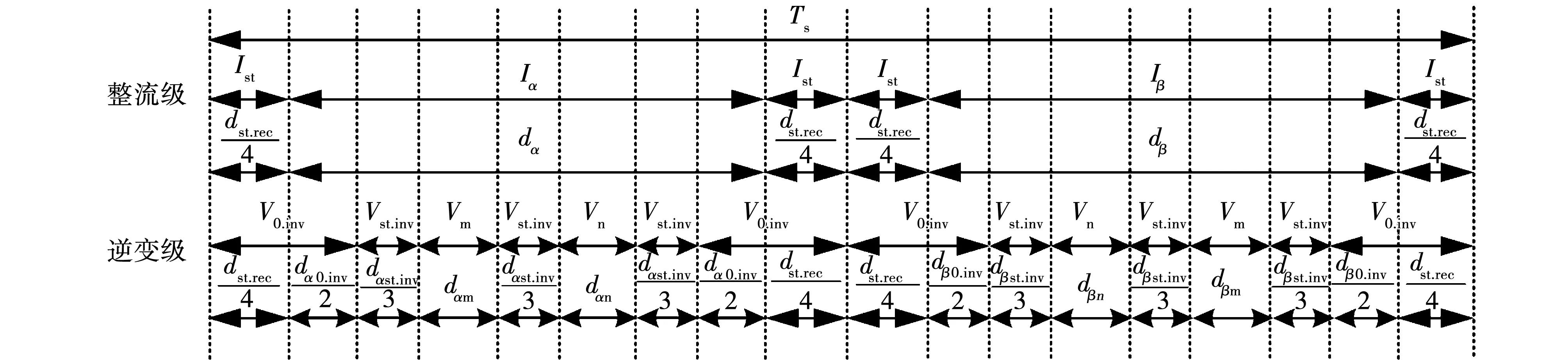
图6 双空间矢量配合的开关时序图Fig.6 Switching sequence diagram of two space vector

4 实验分析

为了说明所提出的双Z源间接矩阵变换器的升压能力大小，在实验平台中对传统的间接矩阵变换器、单Z源的间接矩阵变换器、双Z源的间接矩阵变换器共3种系统结构进行了实验对比，实验参数如表3所示。在实验中，间接矩阵变换器采用空间矢量调制，其中调制系数设置为mi=mo=0.8。

表3 实验参数

图7为三相交流电源的a相电压和输入电流THD。由图可见，三相电源a相的输出相电压为50 V，a相输入电流的总谐波率THD为23.84%。

图7 三相交流电源实验波形 Fig.7 Experimental waveform of three-phase AC power supply

4.1 传统的间接矩阵变换器调制

传统的间接矩阵变换器的最大升压增益仅为0.866。图8为间接矩阵变换器(IMC)的实验波形。其中，图8(a)、(b)、(c)、(d)分别为间接矩阵变换器输出的A相电压、线电压、A相电流以及输出电流THD。由图可见，与图7的输入a相电压相比，没有升压能力，反而降低了输入电压，由于矩阵变换器前加入LC滤波器，输出的电流总谐波率降为16.69%，降低了输入a相的电流谐波。

图8 IMC实验波形Fig.8 Experimental waveform of IMC

4.2 单Z源间接矩阵变换器调制

将单个准Z源网络与间接矩阵变换器结合，得到准Z源网络矩阵变换器(QZS-MC)，它能够有效地提高电压增益。其中分为两种情况，一为准Z源网络在整流级前面[16]，二为准Z源网络在逆变级前面。其中直通占空比D都设置为0.1，则升压因子B=1.25。调制系数mi=mo=0.8。其他条件与MC调制相同。当调制系数不同时，由于直通占空比与调制系数之间限制关系，从而改变直通占空比D大小，会导致输出电压不能达到预期效果。

4.2.1 准Z源网络在整流级前

图9为准Z源网络在整流级前的QZS-MC实验波形其中，图9(a)、(b)、(c)、(d)分别为这种矩阵变换器输出的A相电压、线电压、A相电流以及输出电流THD。由图可见，QZS-MC的输出电压会有明显的升高，A相输出电压稳定时，最高电压约为70 V，输出线电压最高约为120 V，相比输入的a相电压50 V，电压增益近似为1.4，符合理论研究所得到的升压因子B=1.25。而且输出电流总谐波率为14.32%，降低了输入电流总谐波率。因此，QZS-MC调制要比MC调制较好，能够提高电压增益，降低输入电流谐波。

图9 QZS-MC实验波形 Fig.9 Experimental waveform of QZS-MC

4.2.2 准Z源网络在逆变级前

图10为当准Z源网络在逆变级前的QZS-MC实验波形，其中，图10(a)、(b)、(c)、(d)分别为这种矩阵变换器输出的A相电压、线电压、A相电流以及输出电流THD。由图可见，直流侧输出电压最高可以为80 V，从而可以推出，准Z源网络可以提高直流侧电压，进一步QZS-MC可以获得大于1的电压增益，克服了传统矩阵变换器的缺点，此时输出电流谐波率为8.08%，降低了输入电流的谐波。

图10 QZS-MC(中间)实验波形Fig.10 Experimental waveform of QZS-MC(middle)

4.2.3 单Z源间接矩阵变换器的升压问题

下面以Z源网络在整流级前为例来说明单Z源间接矩阵变换器的升压问题。

理论上，若要输出电压升高到3～4倍，则直通占空比D要在0.333～0.475，由于调制系数的限制，所以调制系数需要修改，设置mi=0.6，mo=0.8，其他参数不变，实验波形如图11所示。由图可知，当升压因子大于4以后，输出电压和输出电流波形会出现振荡；输出电流THD为41.33%，说明输出电流产生大量谐波，会对电网造成谐波污染，不能应用于电网的集成。

图11 调制系数不同时QZS-MC实验波形Fig.11 Experimental waveform of QZS-MC when modulation factor is different

对于两种单Z源间接矩阵变换器调制，突破了传统矩阵变换器最大电压增益0.866，但是由于调制系数限制，导致升压能力有限，电压增益不高。

4.3 提出的双Z源间接矩阵变换器调制

1)整流级、逆变级的调制系数相同时。

当调制系数相同时，即mi=mo=0.8，直通占空比Dinv=0.1时，图12为双Z源间接矩阵变换器(TQZS-MC)结构的实验波形。其中，图12(a)、(b)、(c)、(d)分别为这种矩阵变换器输出的A相电压、线电压、A相电流以及输出电流THD。由图可见，当三相输入相电压为50 V，逆变级直通占空比为0.1时，A相输出最高电压可为136 V，将电压增益提高了2.7倍，能够避免调制系数的限制，而且输出电流谐波率为4.16%，降低输出电流谐波。

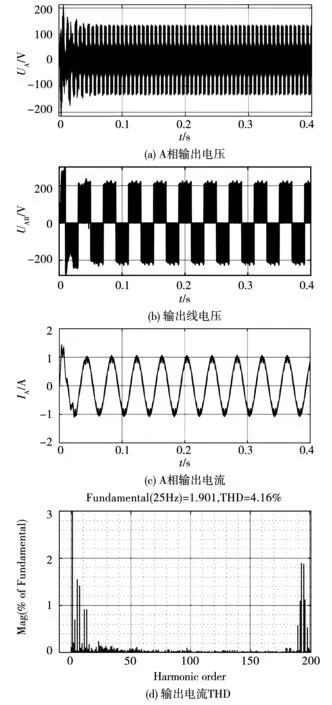
图12 调制系数相同时双准Z源矩阵变换器 (TQZS-MC)实验波形Fig.12 Experimental waveform of TQZS-MC when modulation factor is same

2)整流级、逆变级的调制系数不同时。

当调制系数不同时，即mi=0.8、mo=0.7，且直通占空比Dinv=0.2时，图13为双Z源间接矩阵变换器(TQZS-MC)结构的实验波形。其中，图13(a)、(b)、(c)、(d)分别为这种矩阵变换器输出的A相电压、线电压、A相电流以及输出电流THD。由于调制系数与直通占空比存在的限制，因此将调制系数设置为mi=0.8、mo=0.7，根据式 (11)、(14)、(22)、(29)可推出升压因子B的范围为2.788 9≤B≤4.175，突破了单Z源间接矩阵变换器升压因子不能提高3～4倍的限制。由图可见，当输入电压为50 V时，A相输出最高电压可达到203 V，电压增益提高了4.06倍，理论上升压在设定范围内，而且输出电流谐波率为3.64%，同时降低了输出谐波含量。

图13 调制系数不同时双准Z源矩阵变换器 (TQZS-MC)实验波形Fig.13 Experimental waveform of TQZS-MC when modulation factor is different

通过上面将双Z源矩阵变换器与传统的间接矩阵变换器、单Z源间接矩阵变换器两种结构以及改变参数进行实验比较，可以看出，在相同的实验条件下，3种不同结构调制都能减少谐波含量，但是在单Z源间接矩阵变换器调制中，调制系数过低时，会导致输出谐波增多，不利于电网的集成。与其它两种结构调制不同，双Z源间接矩阵变换器调制能够将电压增益提高3～4倍及其以上，解决了其他结构调制的升压能力不足问题。

5 结 论

本文提出了一种双Z源间接矩阵变换器拓扑结构，它是将两个准Z源网络与间接矩阵变换器结合，在直通占空比有限的情况下，能够获得很高的电压增益。其中两个准Z源分别放在整流级前和逆变级前。针对这种拓扑结构，在理论上推导出电压增益公式，选择正确的开关组合顺序，并通过对比实验验证了该拓扑结构的正确性和优越性。通过本文分析与实验可得到结论如下：

1)双Z源间接矩阵变换器能够避开调制系数的限制，从而可以将电压传输比达到甚至高于4，从而能够提高输出电压；

2)虽然增加的电容和电感以及系统结构变得复杂，但是额外的输入Z源网络可以当作输入滤波器，使得这种拓扑结构不再需要单独的输入滤波器，从而一定程度上简化了系统结构。