本征薄层异质结光伏电池特性拟合曲线与填充因子的线性关系
2021-02-22朱显辉简有为师楠高彬
朱显辉, 简有为, 师楠, 高彬
(1.黑龙江科技大学 电气与控制工程学院,哈尔滨 150022; 2.黑龙江科技大学 工程训练与基础实验中心,哈尔滨 150022)
0 引 言
从本征薄层异质结(heterojunction with intrinsic thin layer,HIT)光伏电池通过在硅晶片上制备非晶硅薄膜的PN结以获得温度和光照的稳定性,在温度变化和长期光照下依然具有较好的输出效率,市场化势头迅猛[1]。准确地给出HIT电池输出特性的I-V曲线,不仅是工况变化时最大功率点跟踪的重要前提,也是提高HIT电池发电效率和成本评估的必要基础。
描述光伏电池输出特性曲线的超越方程含有5个未知参数,而光伏电池数据手册只给出了4个已知条件,无法对超越方程直接求解,因而,求解超越方程5个未知参量的问题广受重视[2],主要方法有以下几类。
一类方法利用化简的手段求解参数。比如,通过忽略串联电阻[3-5]或假定并联电阻为无穷大[6-7],或假定二极管理想因子为常值[8-9],进而给出剩余4个未知参量的值。
另一类方法是构造第5个新方程求解参数,其中比较典型的是假定串联电阻或并联电阻等于特性曲线在开路电压点或短路电流点斜率的负倒数[10-11],或者通过推导温度系数与某一个未知参量等式关系[12-13],寻求光伏电池超越方程未知参量的解。
此外,智能算法在求解光伏超越方程参数中的应用也很多。比如神经网络[14]、遗传[15]、模式搜索[16]、粒子束[17]、差分进化[12]、模拟退火算法[18]等。
上述方法仅能给出超越方程5个未知参数的解,无法直接给出光伏电池输出特性曲线,为得到光伏电池的输出特性曲线,仍需用迭代等方法对已知参数的超越方程进行数值求解[19],而迭代算法不仅仿真时间长,且存在对初值敏感不易收敛等不足[20]。
鉴于上述问题,对无需预先求解参数,且能直接给出光伏电池输出特性曲线的方法进行研究,成为当前的太阳能发电技术的热点。比如,文献[21]、[22]分别采用残差神经网络和径向基神经网络对光伏电池输出特性曲线进行了预测,但该类方法无法摆脱神经网络需要大量训练数据的弊端。文献[23-35]则分别以解析法和泰勒展开式给出了光伏电池的特性曲线,但该类方法仍需预先利用迭代等方法求解超越方程的未知参数。文献[26]基于Lambert W函数实现了特性曲线绘制,但Lambert W函数不属于初等函数,其曲线精确度需以仿真速度为代价。
值得注意的是,Santiago Pindado等在文献[27]给出了一种仅利用手册给定参数,无需求解参数和构造新方程,即可实现光伏电池建模的简单方法,但该方法的建模精确度有待于进一步提高。
本文同样提出一种直接拟合HIT电池输出特性曲线的方法,该方法仅利用厂商给定参数,无需任何实测数据和超越方程求解,基于两条2次贝塞尔函数实现HIT输出I-V曲线的拟合,计算过程简单,并以变端点弦截迭代数值解为参考,对贝塞尔模型和文献[27]模型的误差进行对比,证明本文所提方法的具有更好的精确度,对HIT电池的最大功率的准确跟踪和光伏电站的设计与规划更为有利。
1 基于贝塞尔函数的本征薄层异质结电池建模
单二极管模型和双二极管模型是两种典型的光伏电池的电路拓扑,都可以用来描述HIT电池的输出特性。为简洁起见,本文以单二极管电路为基础讨论HIT电池的输出特性,其拓扑如图1所示。

图1 HIT电池单二极管拓扑Fig.1 Mingle diode topology of HIT cell
图1所示的HIT单二极管模型输出特性满足
(1)
式中:Iph表示光生电流;Io表示二极管反向饱和电流;rs表示串联电阻;rp表示并联电阻;A表示二极管理想因子;T表示HIT的工作温度;K表示Boltzmann常数;Ns表示电池串联个数;q表示电子电量。
可见,式(1)为超越方程,无法用代数方法求解,只能利用迭代等数值计算方法求解。
1.1 两条2次贝塞尔函数的拟合分析
贝塞尔函数是法国工程师皮埃尔·贝塞尔所提出的一种绘制二维曲线图形的数学工具,通过给定曲线的起点和终点之后,利用控制点位置的调整可以方便地实现不同凸凹度的平滑曲线绘制,在曲线设计和微机绘图中应用广泛,形式如下[28]:
(2)
式中:n为次数;Oj为按次序排列的控制点坐标Oj=O(xj,yj);t为相关参数,0≤t≤1,j=0,1,…,n。
第一个贝塞尔贝塞尔函数控制点称为起点,最后一个贝塞尔贝塞尔函数控制点称之为终点,除起点和终点外,n阶贝塞尔函数含有n-1个控制点,控制点数量增加,贝塞尔函数的繁琐性也随着增大。以n=2时为例,2次贝塞尔函数的横、纵坐标计算公式分别为:
(3)
(4)
当t按照某一步长从0到1之间变化时,利用式(3)可得到2次贝塞尔函数计算结果。
并且,在t=0和t=1时,式(3)的值等于O0和O2,分别对应着贝塞尔函数控制点中的起点终点。可知,贝塞尔函数通过其起点和终点两个控制点。
同样,短路电流点,最大功率点和开路电压点是光伏电池输出特性曲线上的三个必经点。鉴于贝塞尔函数计算的复杂性随阶数的升高而增大,为在保证拟合精确度的同时兼顾计算过程的简单性,考虑到HIT电池输出特性曲线的具体特点。本文拟采用两条2次贝塞尔函数对最大功率点左、右两侧的输出特性曲线分别拟合,并以短路电流点和最大功率点为第一条贝塞尔函数的起点和终点,以最大功率点和开路电压点作为第二条贝塞尔函数的起点和终点。
1.2 拟合曲线在最大功率点处的平滑连接
以两条2次贝塞尔函数拟合HIT电池的输出特性曲线,最大功率点为左、右两条曲线的交点,能否保证2条曲线在该点交汇时的平顺性,直接关系到能否对HIT电池最大功率点进行准确跟踪,并且对老化评估和效率分析也有意义。
为行文简洁,后续章节将式(3)和式(4)描述的函数关系称之为贝塞尔函数,将式(3)和式(4)所得的曲线轨迹称之为贝塞尔曲线。
由计算机图形学可知,保证两条贝塞尔曲线在交点处的G0和G1连续,即可保证两条贝塞尔曲线在交点处的平滑连接。
由前述分析可知,最大功率点是第一条贝塞尔曲线的终点,同时也是第二条贝塞尔曲线的起点,满足两条曲线端点重合的G0连续条件。为满足G1连续性,本文拟在平行于开路电压点和短路电流点连线,且经过最大功率点的直线上分别构造两条贝塞尔曲线的控制点。由于2次贝塞尔曲线除起点和终点外,仅包含一个控制点,因而,采用上述手段使第一条曲线的控制点与第二条曲线的控制点位于同一条直线上,满足两条贝塞尔曲线的G1连续条件,既保证了两条贝塞尔曲线的平滑连接,也能有效地简化后续线性关系的研究。
为进一步考察控制点对2次贝塞尔曲线的控制作用,给出选取不同控制点的示意图如图2所示。
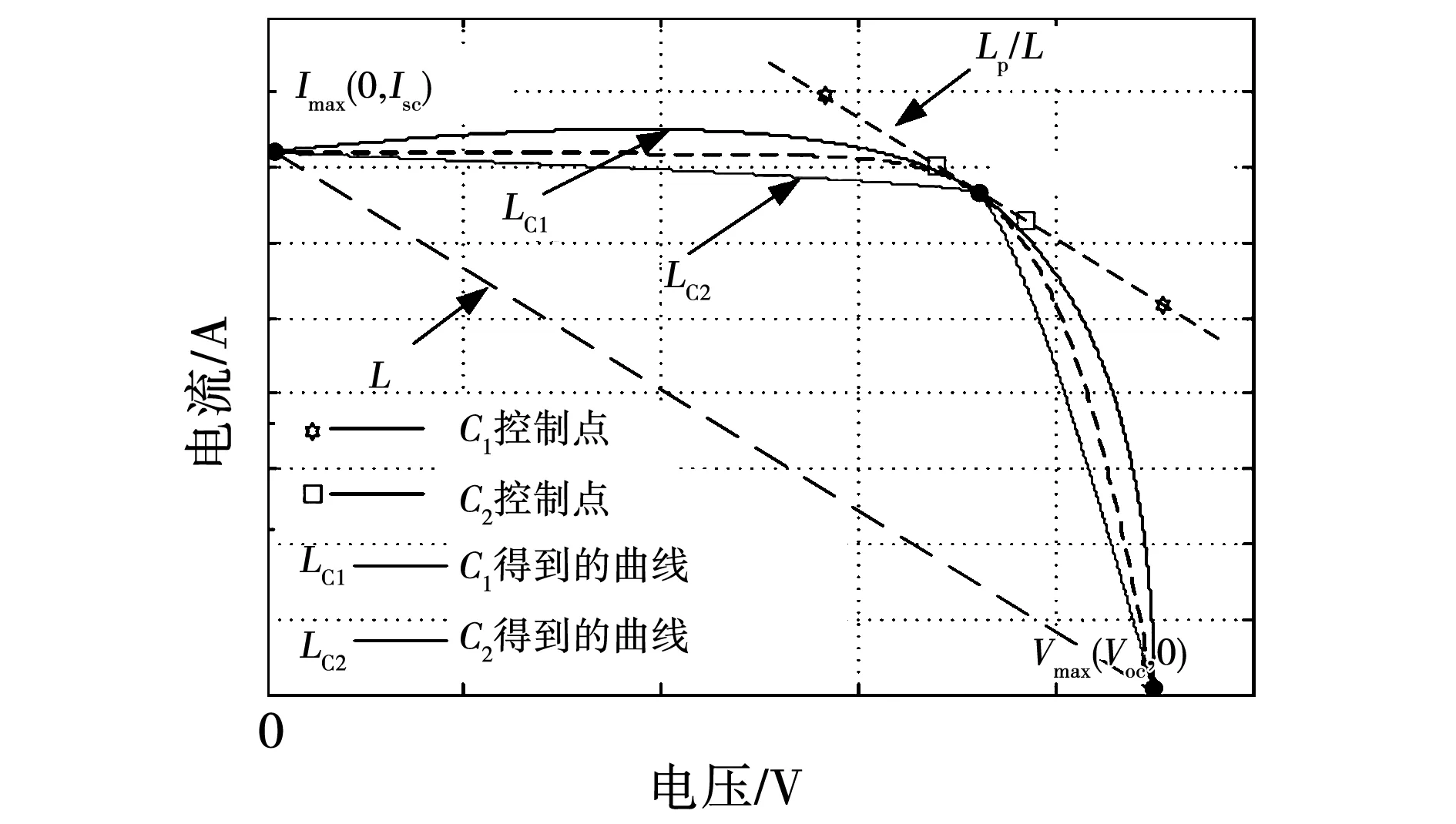
图2 不同控制点的贝塞尔曲线Fig.2 Bézier curves at different control point
图2中:Imax为短路电流点;Vmax为开路电压点;L为连接Imax点和Vmax的线段;Pm为最大功率点;Lp为经过Pm且平行于L的直线。
对最大功率点Pm左侧进行说明如下:在选取Imax和Pm分别作为2次贝塞尔曲线的起点和终点后,在直线Lp上选取控制点为C1和C2时,对应的2次贝塞尔曲线分别为LC1和LC2。最大功率点右侧的贝塞尔曲线和左侧类似,不再赘述。
当Lp上的控制点位于不同位置时,即控制点距离Pm长度不同时,会生成不同凸凹度的贝塞尔曲线,产生不同的拟合效果。则可以得到一条重要推论:通过调整控制点的位置,可以生成的不同的贝塞尔函数,则必然存在着一个最佳控制点,该控制点所生成的贝塞尔曲线与实际的HIT电池输出特性曲线具有较好的匹配效果。
2 变端点弦截迭代数值解的构建
将超越方程的迭代数值解作为光伏电池输出特性误差分析基准的可靠性在文献[29]已经得到充分论证。本文采用变端点弦截迭代法对超越方程进行数值求解,并将所得的数值解误差分析的基准。
迭代算法的应用前提是已知式(1)超越方程的5个未知参数。为此,令Vt=AKT/q,在忽略常数项后,将短路电流点(0,Isc)和开路电压(Voc,0)代入式(1),可得:
(5)
(6)
将(5)代入式(1)得
(7)
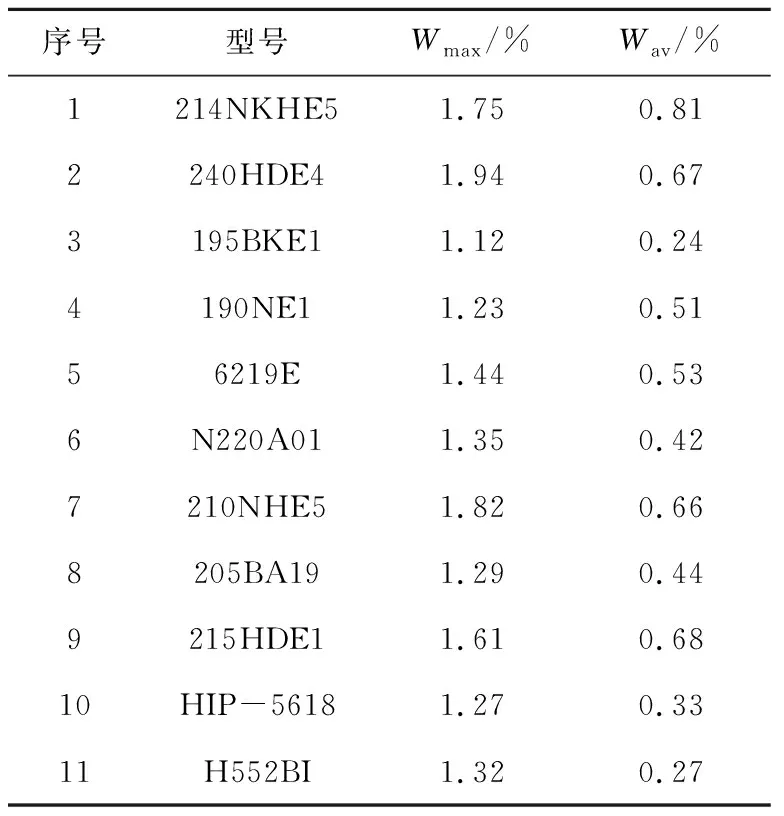
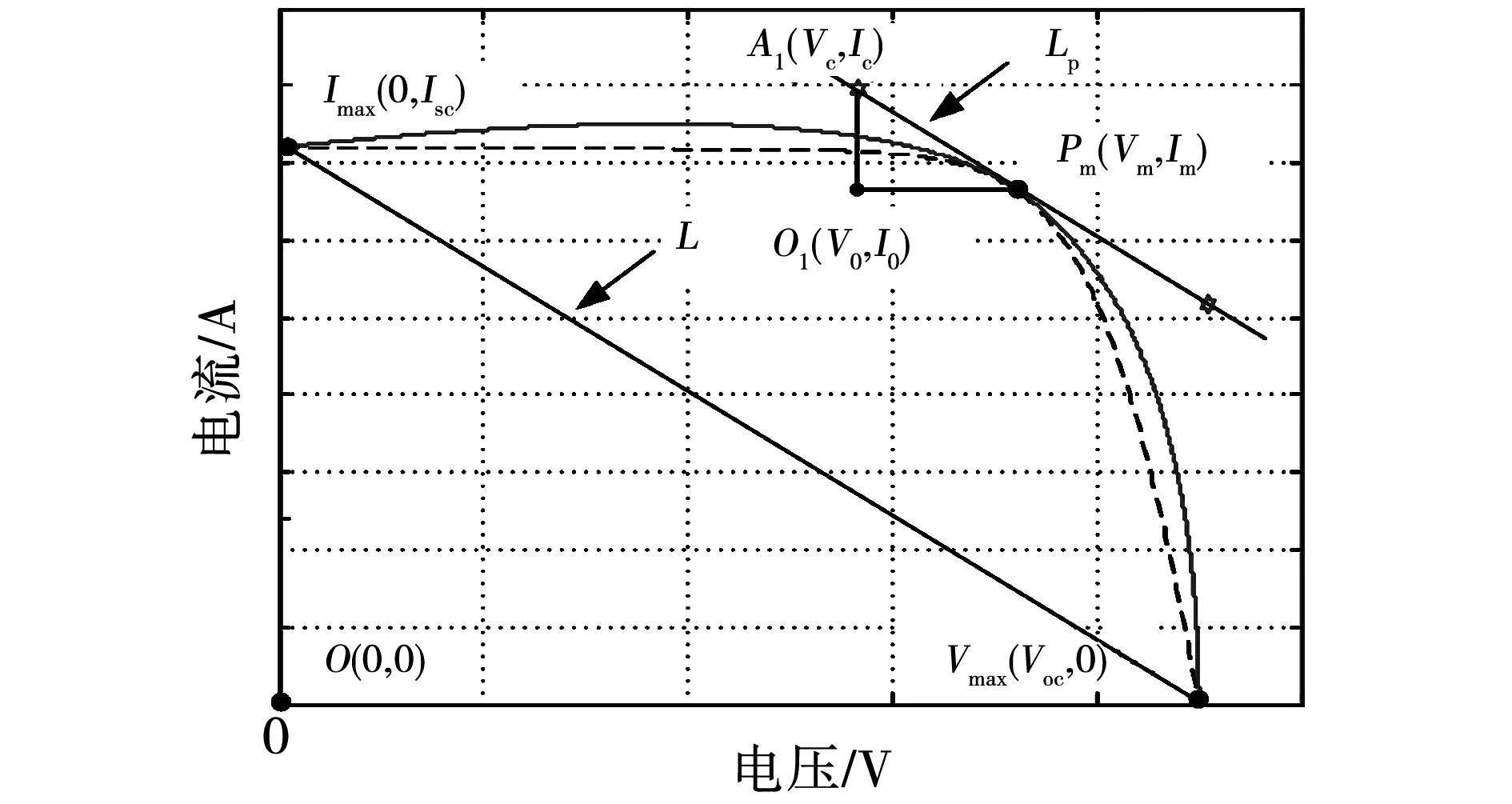
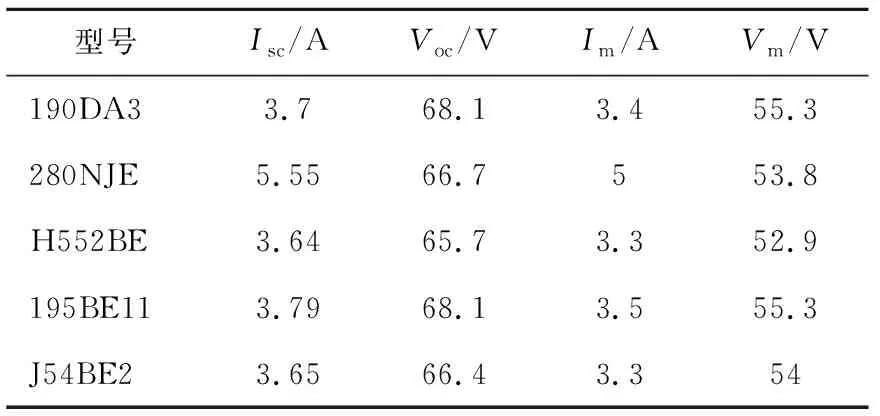
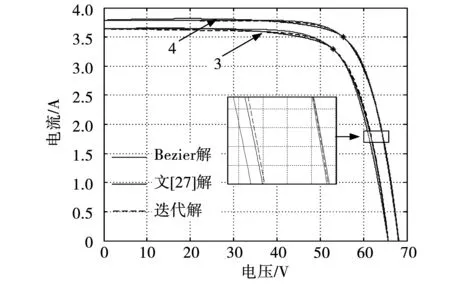
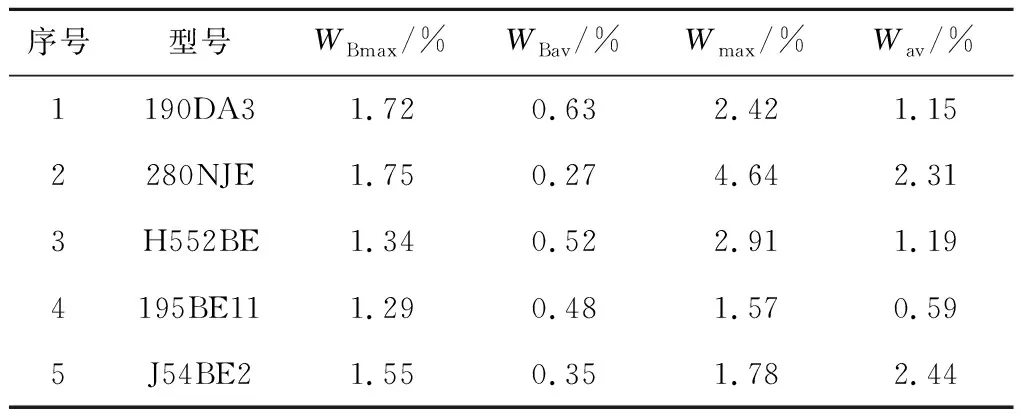
将式(5)代入式(6),由于Iscrs< (8) 将最大功率点Pm(Vm,Im)代入式(1)得 (9) 将式(5)、式(6)代入式(9),消去Io和Iph,令rs+rp=R,可得 (10) 由最大功率点处导数为0,可得 (11) 利用短路电流点(0,Isc)处电压导数等于并联电阻的负倒数,有 rp= (12) 对式(10)~式(12)所示的隐函数,可利用变端点弦截算法求解,变端点弦截迭代算法以相邻两点的差商代替牛顿迭代中的一阶导数,通用形式为 (13) 式中:f()为目标函数;X为所求变量;w当前迭代次数。 将式(10)~式(12)转化为式(13)的迭代形式,结合式(5)和式(8),即可给出HIT电池隐函数的所有未知参量的数值解,具体流程如图3所示。 图3 迭代流程图Fig.3 Iterative flow chart 利用图3步骤,对11种不同型号的HIT电池参数进行计算,结果如表1所示。 表1 HIT电池参数 基于表1的HIT电池的参数计算结果,需再次利用变端点弦截法求解式(1)的超越方程,就可以给出HIT光伏电池输出特性曲线,并将该曲线作为后续章节的误差分析基准。 基于贝塞尔函数的HIT光伏电池建模思路,分别对表1中的HIT电池进行建模,找到误差最小时控制点位置,并将其作为最佳控制点。11种HIT光伏电池的贝塞尔曲线拟合效果如图4所示。 图4 11种HIT电池计算结果与实测结果Fig.4 Computed and measured results for 11 types of HIT cells 图4中用数字表示不同的HIT光伏电池型号,具体的数字与型号的对应关系与表2一致。 以变端点弦截迭代计算结果为基准,将最佳的贝塞尔函数拟合结果的误差进行分析,如表2所示。 表2 贝塞尔函数拟合误差 表2中Wmax为HIT电池贝塞尔曲线拟合结果的最大相对误差,Wav为对应的平均相对误差。由表2可见,利用贝塞尔函数对11种不同HIT光伏电池拟合结果中,最大相对误差均小于1.94%,最大平均相对误差小于0.81%,拟合效果较好。 为探索最佳拟合效果时贝塞尔曲线控制点的分布规律,给出在选取某一控制点时贝塞尔曲线的拟合示意图,如图5所示。 图5 控制点位置的几何关系Fig.5 Geometric relationship of control point position 由图5可以看出,三角形ImaxOVmax和三角形A1O1Pm为相似三角形,利用相似三角形理论可以确定贝塞尔函数控制点的位置。 HIT电池输出特性曲线在最大功率点左侧的曲线,是一条从短路电流点Imax平滑变化到最大功率点Pm的曲线,该部分曲线电压变化范围为0~Vm,电流变化的范围为Isc~Im,右侧曲线电压变化范围为Voc~Vm,电流变化的范围为Im~0。 为寻求不同的贝塞尔曲线控制点与输出特性曲线电压及电流的变化范围之间的线性关系,考察HIT电池的填充因子 (14) 在图5中,定义控制点A1(Vc,Ic)到最大功率点Pm(Vm,Im)的长度LAP与短路电流点Imax到开路电压点Vmax长度LIV的比值l(左、右侧分别表示为lf、lr),作为纵坐标,以填充因子FF作为横坐标,寻求贝塞尔曲线控制点位置与FF之间的内在联系,结果如图6所示。 图6 11种HIT电池控制点拟合规律Fig.6 Fitting law of control points of 11 HIT cells 为进一步验证所提线性关系在HIT光伏电池建模中的准确性和有效性,重新选取5种不同型号的HIT电池进行贝塞尔函数建模,并与文献[27]的建模结果进行对比。 文献[27]模型的算法为,在最大功率点左侧部分I-V特性曲线满足 Il=Isc(1-(1-Im/Isc)(Vl/Vm)Im/(Isc-Im))。 (17) 在最大功率点右侧部分I-V特性曲线满足 Ir=ImVm/Vr(1-((Vr-Vm)/(Voc-Vm))η)。 (18) 5种电池的型号及参数如表3所示。 表3 新HIT电池参数 基于表3中厂商给定参数,利用式(15)、式(16)分别确定2条2次贝塞尔函数控制点位置,进而给出贝塞尔函数的输出特性拟合结果,利用式(17)、式(18)既可以计算文献[27]模型的HIT电池输出特性拟合结果,如图7、图8所示。 图7 3种新HIT电池输出特性曲线Fig.7 Output characteristic curves of 3 new HIT cells 图8 2种新HIT电池输出特性曲线Fig.8 Output characteristic curves of 2 new HIT cells 图7、图8中同样用数字代表HIT电池的型号,数字与型号的对应关系详见表4,表4中给出了图7、图8的误差分析结果。 表4 新HIT电池计算误差 由表4结果可知,贝塞尔函数对5种HIT电池的输出特性建模的最大相对误差分别为1.72%、1.75%、1.34%、1.29%和1.55%。平均相对误差分别为0.63%、0.27%、0.52%、0.48%和0.35%;文献[27]模型的最大相对误差2.42%、4.64%、2.91%、1.57%和1.78%。平均相对误差分别为1.15%、2.31%、1.19%、0.59%和2.44%。贝塞尔函数建模的精确度优于文献[27]模型,证明了所提方法的有效性和准确性。 进一步给出贝塞尔函数左、右两侧控制点位置与填充因子FF之间的线性拟合关系式分别为: lf=-0.553 2FF+0.529 8; (15) lr=-0.408 5FF+0.457 9。 (16) 基于式(15)、式(16)给定的线性关系,可实现无需任何实验数据,仅利用厂商数据手册给定的FF、开路电压点、短路电流点和最大功率点数据,即可实现对不同HIT电池输出特性曲线的简单拟合。 本文主要围绕着本征异质结这一特定光伏电池结构,在其市场化进程的起始阶段,重点针对本征异质结光伏电池输出特性曲线的建模问题进行研究,得到如下结论: 1)提出了2次贝塞尔曲线对HIT光伏电池输出曲线最大功率点左、右两侧分别拟合的思路,并给出了在经过最大功率点且平行于短路电流和开路电压连线的直线上取控制点的方式,保证了2次贝塞尔函数在最大功率点处平顺连接。 2)得出了两条2次贝塞尔曲线最优控制点位置与HIT光伏电池填充因子之间的线性关系,实现了简单、准确的,无需繁琐迭代和实验测试,仅需厂商给定数据的HIT电池输出特性建模方法。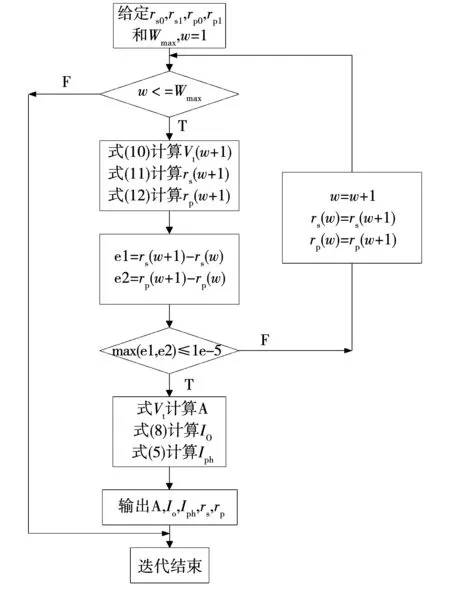
3 变端点弦截迭代数值解的构建
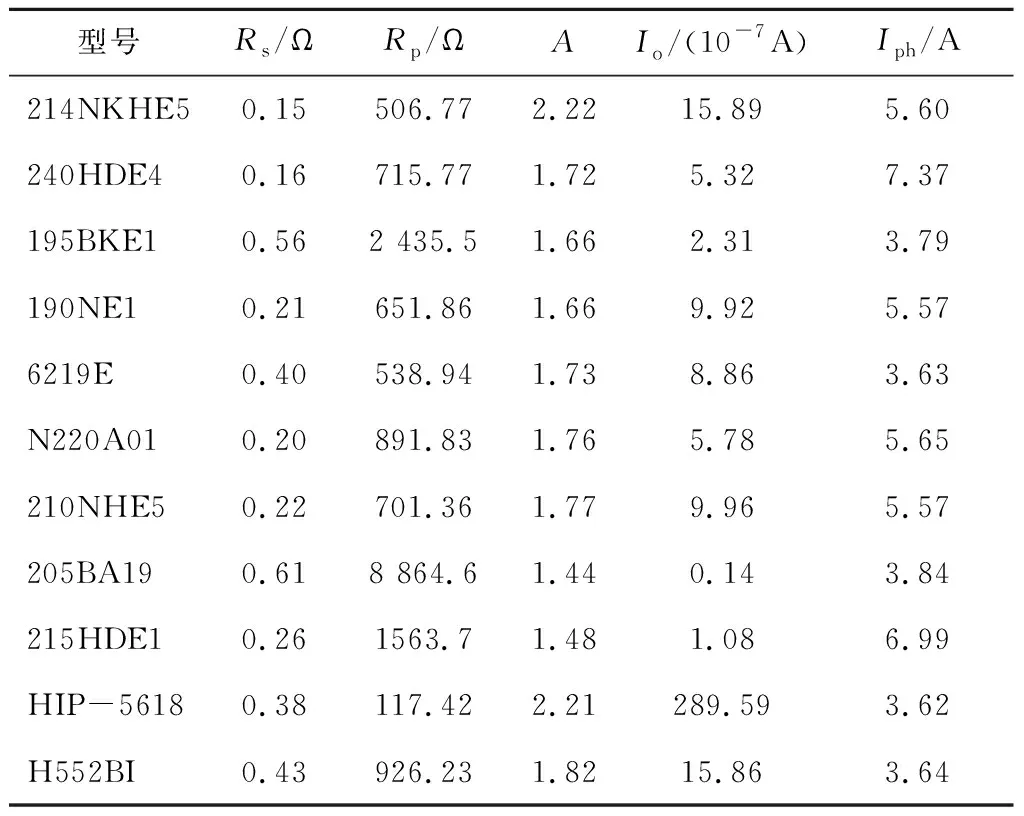
4 贝塞尔曲线最佳控制点分布规律及验证

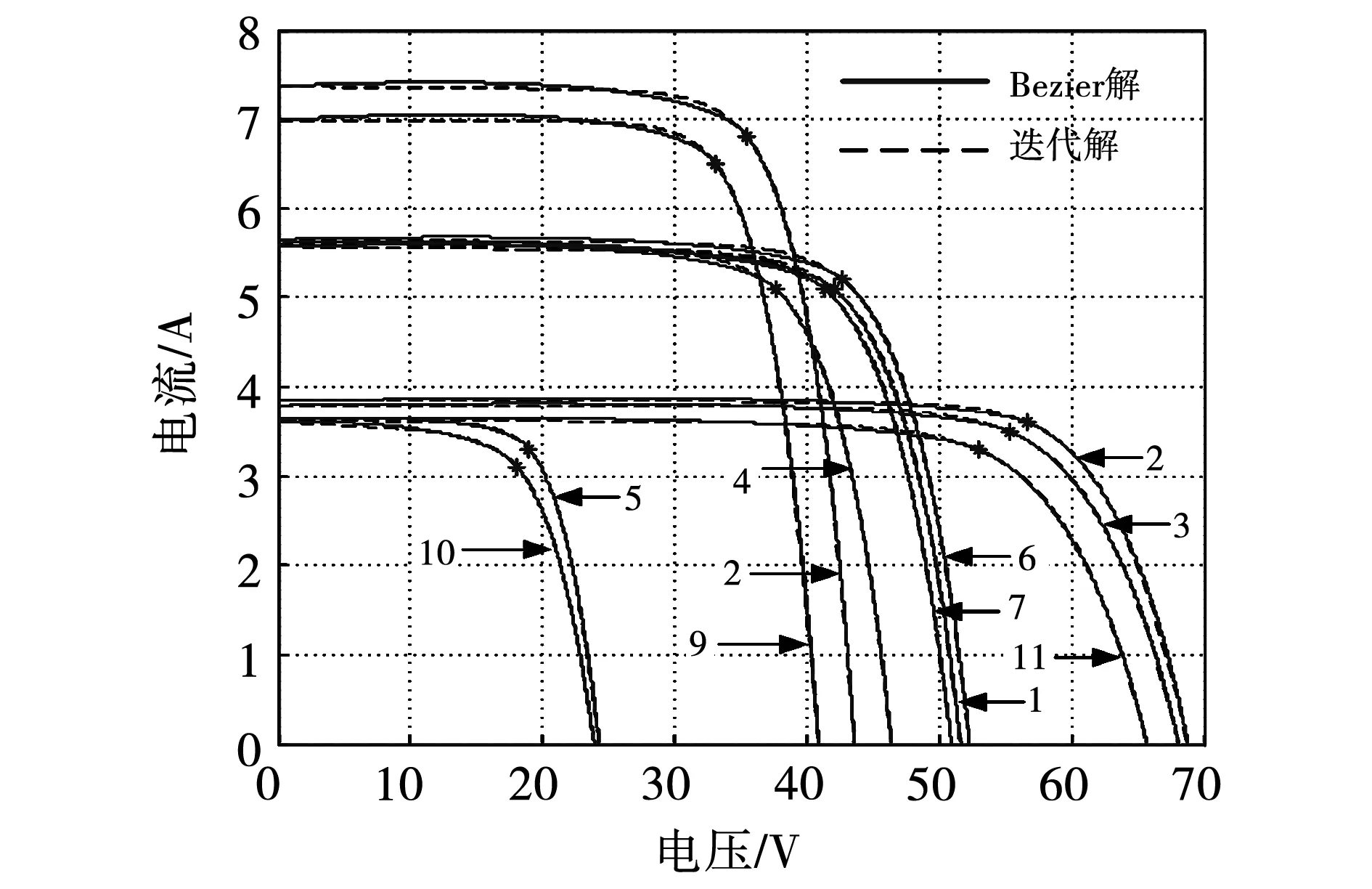
5 模型的验证与对比分析
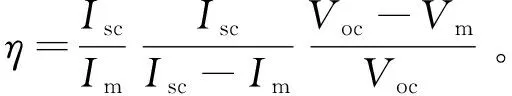

6 结 论
