三相电压源型逆变器馈电两相混合式步进电机预测电流控制

王春雷， 曹东兴， 曲祥旭， 胡慧

(1.河北工业大学 机械工程学院，天津 300130； 2.天津铁道职业技术学院，天津 300240)

0 引 言

步进电机具有制造成本低，可靠性高和开环控制等特点，广泛用于工业和消费类应用，例如计算机数控、机械臂、扫描仪、打印机等[1]。步进电机可以工作于开环或闭环模式，两种模式具有相似的驱动拓扑，即每个定子绕组由一个独立的H桥驱动，每个H桥又使用一个电流控制器按照参考电流变化规律调节绕组电流。

开环模式下，不需要使用昂贵的位置传感器，这对于普通工业应用或民用具有很强的吸引力[2]。由于没有位置传感器，位置或速度控制器无法实时获取转子的实际位置和速度信息来产生电流控制器需要的参考电流，因此参考电流的波形需要预先确定。通常选择定子绕组所允许的最大电流幅值作为参考电流幅值，使电机输出最大扭矩以避免失步现象的发生。这种非最优驱动方式存在能效低、转矩脉动大和共振等问题[3]。微步(microstepping)技术可以改善步进电机的转矩特性，提高定位精度，使得步进电机能够用于要求更高的场合，因此广泛应用于开环控制中[4]。然而，开环控制中固有问题仍然存在，如由负载转矩变化导致的失步和低能效等。闭环控制可以有效解决上述问题，随着电力电子技术的发展和现代控制理论的进步，其在步进电机上得到广泛应用。闭环控制通常采用级联结构，即：外部位置(速度)控制器通过采集的转子位置和速度等信息利用磁场定向控制(field oriented control，FOC)动态调节参考电流波形，内部电流控制器按照该参考电流调节绕组电流。

可见，上述开环或闭环控制是相对于位置和速度而言的。针对定子绕组电流的控制，通常采用比例积分(proportional integral，PI)[5]、滞环[6]和模型预测控制(model predictive control，MPC)[7]等闭环控制策略。然而，在步进电机这种典型的非线性系统上应用线性PI控制难以获得令人满意的效果。滞环控制对参数变化和负载转矩扰动具有很强的鲁棒性，但存在电流脉动较大且由于电子开关频率可变进一步增加开关损耗和电磁干扰。MPC拥有数十年的应用历史，这得益于其概念直观、实现简单、具有良好的动态性能并可以直接处理非线性和约束等问题[8]。早期工业应用中，MPC的应用仅限于缓慢变化的过程工业，随着微处理器技术的进步和更强大的数字信号处理器的出现及其不断增强的计算能力，MPC已成功应用于快速变化的系统，如VSI和电机驱动器。

MPC应用于VSI时可分为有限控制集模型预测控制(finite control set MPC，FCS-MPC)和连续控制集模型预测控制(continuous control set MPC，CCS-MPC)[9]。CCS-MPC使用预测模型来计算连续控制信号，然后使用调制器生成VSI所需的信号，由于调制器的存在，开关频率是恒定的。FCS-MPC利用VSI固有的离散特性，仅评估VSI有限数量的开关状态，通过最小化代价函数来解决优化问题，然后将最佳控制动作直接施加到VSI，因此不需要调制器，实现简单。

无差拍控制、FCS-MPC和CCS-MPC等预测控制已广泛应用于感应电机[10]、无刷直流电机[11]和永磁同步电机[12]中，然而，在步进电机上鲜有应用。文献[7]利用两个具有相同结构的离散时间MPC分别调节同步d-q坐标下的直轴电流id和交轴电流iq。离散MPC为优化问题提供了在线解，可以使用有利于提高系统稳态性能的长时域预测控制而不会显著增加计算成本，但在CCS-MPC中很难加入约束，如果控制信号超过约束条件，将导致性能显著下降。

针对步进双H桥驱动拓扑模式中，每相电流都需要一个独立控制器，常用的PI控制器自适应性、鲁棒性较差，滞环控制器存在电流脉动较大和电磁干扰，CCS-MPC求解困难且难以加入约束等问题。提出了三相VSI馈电两相混合式步进电机(hybrid stepper motor，HSM)预测电流控制，实现了有限控制集模型预测电流控制(finite control set model predictive current control，FCS-MPCC)和无差拍预测电流控制(deadbeat predictive current control，DPCC)两种典型预测控制策略。通过建立电压控制集，电流预测模型及代价函数实现了无需调制器的FCS-MPCC；最后，改进空间电压矢量调制(space voltage vector pulse width modulation，SVPWM)以满足非平衡电路结构的要求，实现了DPCC。仿真和实验验证了两种预测控制算法的有效性及可行性，比较了两者的动、静态性能并确定其应用场景。

1 步进电机及逆变器数学模型

1.1 两相混合式步进电机数学模型

简化的两相双极性HSM模型包括一个永磁转子和两个相隔90°的定子绕组，状态方程表示为：

(1)

式中：θ是转子机械(角)位置；ω是转子(角)速度；va、vb和ia、ib分别表示绕组A和B的电压和电流；B是粘滞摩擦系数；J是转子转动惯量；Km是电机转矩常数；τL是负载扰动；R是定子绕组的电阻；L是定子绕组的电感；Nr是转子齿数。

1.2 三相电源型逆变器数学模型

图1 三相两级VSI馈电两相HSMFig.1 Three-phase two-level VSI fed two-phase HSM

控制信号Sx=1，打开相应桥臂上的电子开关；Sx=0则关断电子开关。因此，3个控制信号形成8种开关状态组合及8个电压矢量(voltage vector,VV)，在α-β坐标下用Vj表示VV，j=0,1,2,…,7。8个VV形成了一个非对称的空间六边形，如图2所示。该非对称六边形被等分成6个扇区，非零量V1、V2、…、V6依次位于第Ⅰ、Ⅱ、 …、Ⅵ扇区上，而两个零电压V0和V7则位于非对称六边形圆心上。

图2 α-β坐标下电压矢量及相应的开关状态Fig.2 VVs and corresponding switch states in α-β frame

2 有限控制集模型预测电流控制

FCS-MPCC主要利用了VSI具有有限数量开关状态的特性来简化MPC优化问题。控制算法主要包括：1)通过枚举VSI所有允许的开关状态来预测绕组电流；2)通过自定义的代价函数来评估所有预测电流的性能；3)将具有最小代价函数值VV对应的开关状态直接应用于VSI。

2.1 电流预测模型

将式(1)中电压状态方程写成复向量的形式为

(2)

式中is=ia+jib和vs=va+jvb分别表示绕组电压和绕组电流，va和vb分别为电压控制集中Vj在α和β轴上的投影。对于小采样间隔Ts，可以用一阶前向欧拉法离散式(2)，得到离散化预测模型为

jKmω(k)ejNrθ(k))。

(3)

由于两个零VV产生的预测电流相同，电压控制集中需只包含一个零VV，即电压控制集由6个非零电压(V1,V2,…,V6)和1个零电压(V0或V7)组成。控制算法需利用式(3)计算控制集中每一个VV对应的电流值。

2.2 代价函数

控制算法利用代价函数评估预测电流的质量来确定最优开关状态。代价函数形式十分丰富，如模型预测转矩和磁通控制中的代价函数一般由多个部分组成，这需要为不同组成项选择合理的加权系数，加权系数的选择需要通过大量的实验并结合经验值来完成。FCS-MPCC代价函数的形式则相对简单，仅包含一个电流项，即

(4)

(5)

为了提高HSM的安全性和稳定性，需要限制流经定子绕组的最大电流。通过在代价函数中添加一个约束项g1来实现，有

(6)

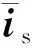
2.3 延时补偿

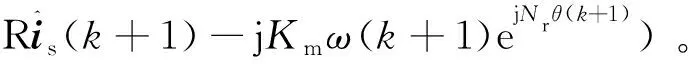
(7)

代价函数也调整为

g=g0(is(k+2))+g1(is(k+2)) 。

(8)

2.4 FCS-MPCC算法概述

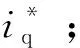
图3 FCS-MPCC框图Fig.3 Block diagram of the FCS-MPCC

FCS-MPCC算法概述如下：

1)在第(k)控制周期，测量定子电流is(k)，定子电压vs(k)，转子机械位置θ(k)，及转子机械角速度ω(k)；

2)将上一个控制周期计算的最优开关状态so(k)直接应用于逆变器；

5)使用代价函数评价第k+2个控制周期预测的7个电流，并存储最优电压和最优开关状态。

3 无差拍预测电流控制

3.1 无差拍预测电流控制原理

jKmω(k)ejNrθ(k)。

(9)

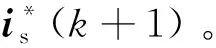
由于同样存在计算延时，实现DPCC算法时，通常采用一步超前预测策略来补偿计算延时。该补偿策略特点是将当前控制周期计算的命令电压vs(k+1)在下一个控制周期应用于VSI。由于控制周期足够小，忽略转子机械位置和速度得变化，右移式(9)得到

(10)

(11)

3.2 SVPWM参数确定

图4 第Ⅰ扇区命令电压矢量分布图Fig.4 Distribution of command VVs in sector Ⅰ

(12)

式中Ts为控制周期，T0、T1和T2分别为零电压(V0或V7)以及非零电压V1和V2的作用时间。当控制周期Ts足够小时，可简化为

(13)

(14)

(15)

(16)

确定了SVPWM的时间参数后，还需要确定控制信号S1、S2和S3的波形模式。波形模式的设计准则是波形易于实现且近似输出恒频率，由于恒频率可以有效降低总谐波失真(total harmonic distortion，THD)。由此，采用的波形模式具有如下特征：

1)控制信号的波形中心对称，该模式的波形容易实现且不存在附加谐波。

2)使用Sabc表示开关管S1、S2和S3的控制信号，在每一个控制周期，波形开始于S000同时结束于S000，因此，逆变器输出的电压开始于V0同时也结束于V0。

3)将零电压V7对应的开关状态S111插入到控制信号对称中心，因此，除了占空比是0%和100%的特殊情况，在一个控制周期内电子开关需要完成开、关各一次的动作，这样可以近似输出恒定开关频率，改善了电流质量。

图5 第Ⅰ扇区通用的控制信号波形模式Fig.5 Generalized waveform pattern for VVs in sector Ⅰ

图6 第Ⅰ扇区特殊控制信号的波形模式Fig.6 Special waveform patterns for VVs in sector Ⅰ

3.3 DPCC算法概述

基于DPCC实现的速度调节器如图7所示，可见，其与FCS-MPCC的显著区别在于SVPWM的使用。

图7 DPCC框图Fig.7 Block diagram of the DPCC

DPCC算法概述如下：

1)在第k控制周期，测量电流is(k)，转子机械位置θ(k)及角速度ω(k)等信息；

2)使用改进的SVPWM调制上一个控制周期计算的命令电压vs(k)；

4 仿真与实验

4.1 仿真分析

在MATLAB/Simulink环境中进行了仿真实验以评估新驱动拓扑结构下预测控制器的性能。两相HSM的主要参数在表1中列出。此外，电流控制频率为50 kHz，速度控制频率为10 kHz，速度PI控制器增益Kp=0.005 21，Ki=2.79。

表1 两相HSM主要参数

第一个仿真实验评估了空载条件下两类预测控制的暂态和稳态性能。参考速度ω*分别于0、0.1和0.2 s时刻阶跃到360、720和360 r/min，速度、扭矩和电流响应如图8所示。FCS-MPCC和DPCC的转速ωf和ωd紧密的跟踪着ω*，其中建立时间约0.03 s且无稳态误差，如图8(a)所示。图8(b)所示的扭矩响应中，稳态参考扭矩τ*由360 r/min时的0.22 N·m增加到720 r/min的0.42 N·m，FCS-MPCC和DPCC的扭矩τf和τd按照参考扭矩变化规律实时调整，但FCS-MPCC存在较大的扭矩脉动。

步进电机的速度及扭矩响应性能与绕组电流的质量有着紧密的关系。步进电机瞬时转矩τ由电磁转矩和磁阻转矩组成。电磁转矩由定子绕组电流和转子磁通量相互作用产生的转矩τe与定位转矩τd组成[15]。定位转矩τd约为电磁转矩的1～10%，不会显着影响电机产生的扭矩，故被忽略。同样忽略磁阻转矩τr，由于τr取决于交、直轴之间磁阻的变化，可以通过保持id=0来取消。最终，瞬时扭矩简化为τ=Kmiq。因此，通过改善电流质量可以改善速度、扭矩响应性能。

FCS-MPCC和DPCC的电流响应如图8(c)和(d)所示，电流按照正弦规律变化，幅值正比于转速，转速为360 r/min和720 r/min时电流频率分别为300 Hz和600 Hz，即电流频率等于转子频率与转子齿数的乘积。验证了由于转子多齿结构的限制步进电机很难在高速(>1 000 r/min)下运行。

图8 空载条件下，HSM速度、扭矩和电流响应Fig. 8 Speed,torque,and current responses of HSM without load torque disturbance

结果表明，空载条件下两类预测控制都具有较好的动、静态性能。但FCS-MPCC的扭矩、电流脉动显著偏高。这是由于DPCC通过SVPWM调制的连续控制信号来调节电流；而FCS-MPCC在有限的7个VV中选择最优VV后将其对应的开关状态量直接应用于VSI。

第二个仿真实验评估了参考速度恒定时，负载转矩扰动对系统的影响。实验中，参考速度在0～0.3 s内保持在540 r/min，一个0.4 N·m恒负载转矩于0.1 s施加到系统且于0.2 s释放，速度和扭矩响应如图9(a)和(b)所示。当扰动出现瞬时，转速下降到约320 r/min，然后经过0.03 s调整恢复到参考转速；扰动消失瞬间，转速上升到760 r/min，经过0.03 s调整后恢复到参考转速。可见，转矩扰动对转速有较大影响，具体应用中可在系统中加入扰动观测器(如龙贝格扰动观测器和滑模观扰动测器)和前馈补偿装置来观测并补偿负载扰动给速度调节器来改善系统性能[16-18]。

图9 负载扭矩扰动时，HSM速度、扭矩和电流响应Fig.9 Speed, torque, and current responses of HSM under load torque disturbance

FCS-MPCC和DPCC的电流响应如图9(c)和(d)所示。电流按照正弦规律变化，幅值由1.1 A增加到2.7 A来克服负载扰动，电流频率近似为450 Hz。由于使用了调制器，DPCC拥有更好的电流质量。

最后一个仿真实验评估两类预测控制的电流THD，空载条件下，在全速域分别使用FCS-MPCC和DPCC调节的A相电流的THD如图10所示。结果表明，在全速域内，DPCC的电流THD在5.0左右波动，相对于FCS-MPCC具有明显的优势，主要得益于改进SVPWM的使用，保证开关频率近似恒定，降低了相电流THD。由于没有使用调制器，FCS-MPCC的电流THD整体较高，但随着转速的升高而降低。

图10 全速域范围内两类预测控制的电流THDFig.10 Current THDs of the two types of predictive control at full-range speeds

4.2 实验分析

在爬楼梯轮椅机器人前腿机构上对两种预测控制进行了对比实验。整个装置由HSM及其驱动器、控制器、带有多级齿轮减速器的机器人前腿机构等组成，如图11所示。采用TI公司的TMS320F28035作为驱动器主控芯片，除电流、速度控制频率减小到20 kHz和4 kHz外，使用的HSM和控制器参数与仿真实验一致，在表1中列出。

图11 实验装置Fig.11 Experimental setup

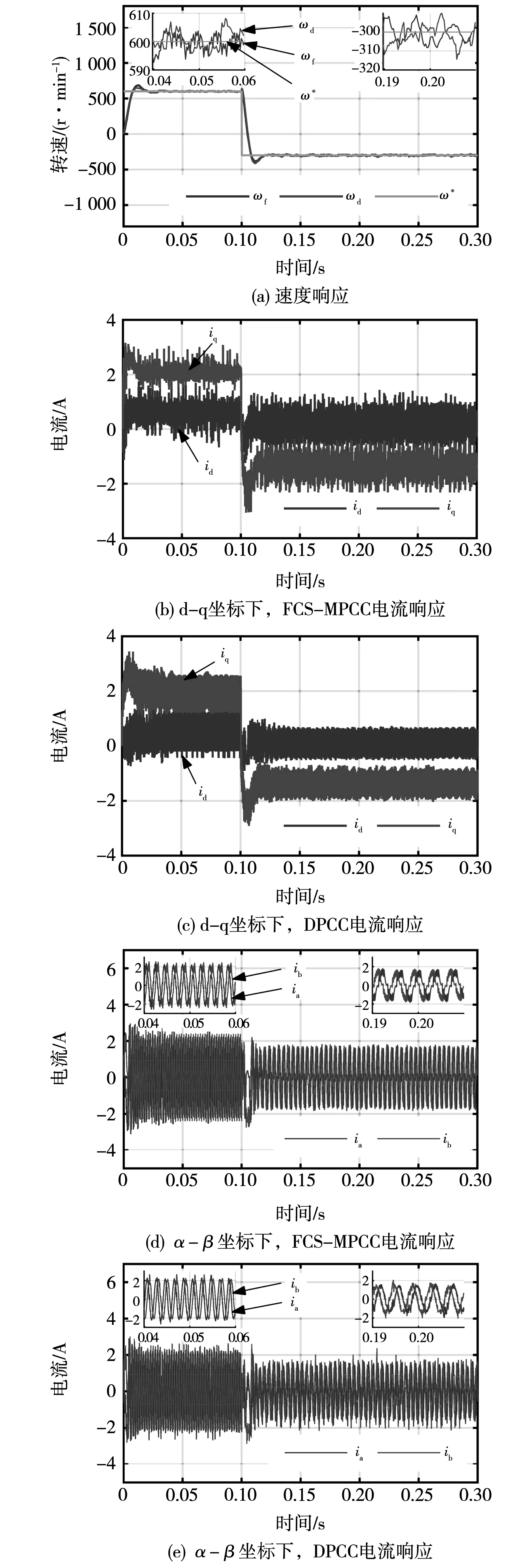
图12 负载条件下，HSM速度和电流响应Fig.12 Speed and current responses of HSM under load

5 结 论

本文研究了三相VSI馈电两相HSM预测电流控制。采用三相VSI取代双H桥，结构紧凑、适应性强且降低了硬件成本。仿真和实验结果表明，提出的两种预测控制器都能够同步调节两相电流且具有良好的动、静态特性，鲁棒性强。FCS-MPCC充分利用VSI电路的离散特性，可直接加入限制，避免求解二次规划难题，实现简单，适用于硬件性能有限、动态性要求较高场合。DPCC使用改进SVPWM调制电压，保证开关频率近似恒定，降低电流THD，能够有效抑制电流和转矩脉动，适用于高精度速度跟踪应用。