索杆式雷达结构型面精度调控方法

2021-02-22唐宝富蒋鸿鹄王金伟蔡建国

东南大学学报（自然科学版） 2021年1期

唐宝富蒋鸿鹄王金伟张骞蔡建国

(1南京电子技术研究所, 南京 210039)(2东南大学混凝土及预应力混凝土结构教育部重点实验室, 南京 211189)

随着雷达技术的不断发展，相控阵技术特别是有源相控阵技术在雷达中得到了广泛的应用[1]，并不断朝着超高带宽、多功能、高性能、高集成和轻量化等方向发展.伴随着电子元器件和微组装技术的不断发展，天线阵面的集成度越来越高，并逐步向结构与功能的一体化设计方向发展[2].然而，雷达结构的轻量化与质量控制、集成度和高性能等多方面需求间存在着相互制约的关系[3].传统雷达结构通常采用提高结构尺寸的方式满足结构刚度和指向精度等方面日益严苛的需求，如美国的AN/FPS-85、AN/FPS-108、AN/FPS和俄罗斯的沃罗涅日-M、沃罗涅日-M(增强型)等均采用钢结构支承方案，结构质量较大，造价昂贵.

索杆结构采用拉索代替受拉杆件，极大地降低了结构质量，并且通过设定预应力的方式提升结构刚度，逐步在雷达结构中得到应用，尤其是相控阵雷达结构[4-5].然而，雷达通常在太阳照射、风、冰雪、振动、冲击、盐雾、湿度等复杂环境中服役，随机、时变的动态环境会引起型面变形，进而影响雷达性能.面向复杂环境的高适应性与型面的高精度要求[6]，通过引入结构主动控制系统来提高雷达结构的稳定性.主动控制的优势在于通过传感器和作动器来识别与调控结构响应，以应对复杂多变环境[7].

主动控制的前提在于信号的收集，在雷达结构中主要为型面变形信息.传统变形监测方法主要有光学成像法和基于应变信息的变形场监测方法.光学成像法为直接监测法，包括投影云纹干涉法[8]和立体模式识别法[9-10].基于应变信息的变形场监测方法是一种间接监测方法，通过设计算法将表面应变信息重构为变形场[11-16].然而，光学成像法目前仅适用于实验室环境，而基于变形信息的变形场监测方法需要消耗较大的计算资源，因此在实际服役过程中，需要更为高效的信号收集系统.

雷达结构型面变形会引起支撑体系的变形与内力变化.当支撑体系为索杆体系时，基于索杆结构中拉索内力对型面变形的高敏感性，建立型面变形与拉索内力变化的对应关系，可设计出一种以拉索内力变化为信号的主动控制机制.由于索力监测相较于应变场监测更为简单，且索力对于微小变形的反应更为敏感，因此该主动控制系统具有一定的优越性.在索杆结构中通过控制撑杆伸缩调整荷载路径，实现抵抗外荷载作用的目的[17].

本文提出了一种新型的鱼腹式索杆雷达结构，并分析了索力与型面变形的映射关系.引入撑杆伸缩的主动调控方法，搭建了基于监测索力和驱动撑杆的雷达结构主动控制系统，并进行了平面鱼腹梁和空间鱼腹索杆式雷达结构的算例分析.

1 索杆式雷达结构

根据相控阵雷达的设计要求，提出了一种新型的预应力索杆式雷达结构，主要由阵面面板、索杆支撑体系和环梁体系组成(见图1).索杆支撑体系采用鱼腹式形式，由双向四榀鱼腹式单元交错组成.鱼腹式单元包含拉索(谷索和脊索)与撑杆.拉索端部固定于外圈环梁处.撑杆布置于谷索与脊索之间，且在端部连接阵面面板.通过在拉索中施加预应力提高结构刚度，在部分撑杆处布置作动器，控制撑杆伸缩以进行阵面面板型面精度控制，从而提高雷达结构在不同工作环境下的适应能力，具有轻质高强的特点.

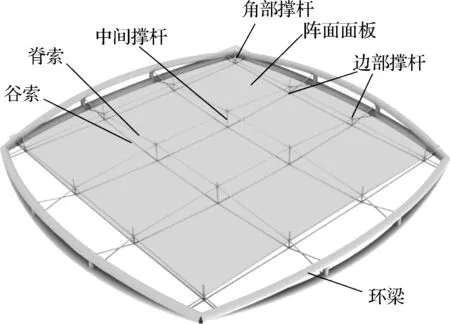
图1 索杆式雷达结构

2 型面精度调控方法

2.1 索杆式结构受力特性分析

2.1.1 有限元分析

如图2所示的二维单撑杆结构体系由梁、两段拉索(脊索和谷索)和单一撑杆组成.梁两端与拉索两端均被固定约束，梁上承受竖向均布荷载作用，荷载方向取向下为正方向.

图2 二维单撑杆结构

二维单撑杆结构中梁跨度为2 m，撑杆长0.2 m，撑杆两侧的脊索和谷索的长度均为1.02 m.脊索和谷索中施加初始预应力均为112.85 MPa.梁采用截面尺寸为50 mm×50 mm×3 mm的方形管，材料弹性模量为70 GPa，密度为2 700 kg/m3.撑杆采用截面直径为20 mm、壁厚2 mm的圆管，材料弹性模量为195 GPa，密度为8 000 kg/m3.拉索采用直径为5 mm的钢丝绳，材料弹性模量为110 GPa，密度为8 000 kg/m3.梁、撑杆和拉索在ABAQUS有限元仿真模型中分别采用B11、T3D2和T3D2单元.

竖向均布荷载为2.0 N/mm时二维单撑杆结构的竖向位移与轴向应力如图3所示.梁发生弯曲变形，跨中最大竖向位移为3.976 mm，撑杆整体下移.谷索伸长导致索应力提升到196.6 MPa，但是脊索缩短导致应力下降到30.9 MPa.撑杆的刚度较大，轴向缩短约0.01 mm，约为撑杆整体竖向位移的0.25%.

(a) 竖向位移

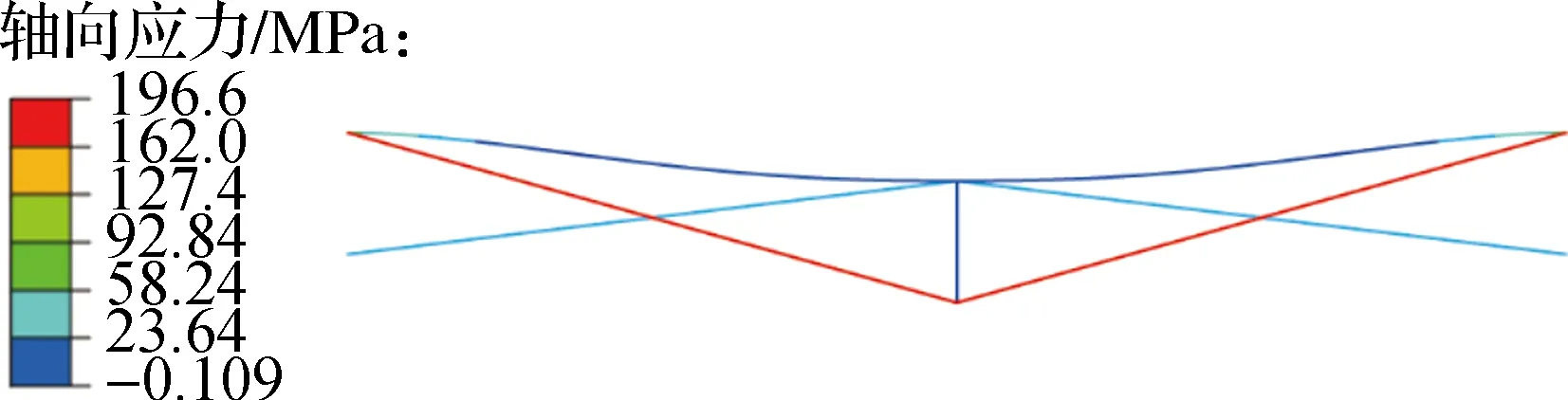
(b) 轴向应力

图4为不同荷载工况下谷索与脊索应力与梁跨中竖向位移的关系曲线.由图可知，谷索应力与梁跨中竖向位移成正比，脊索应力与梁跨中竖向位移成反比，拉索索力与梁跨中竖向位移存在显著的映射关系.在拉索中布置力传感器实时监测索力变化，可间接实现监测梁跨中竖向位移的目的.

图4 不同荷载工况下拉索应力与梁跨中竖向位移的关系

2.1.2 理论验证

在竖向均布荷载作用下，二维单撑杆结构的变形前后状态见图5.图中，L1、L2、Lc分别为谷索、脊索和撑杆的初始长度；Δ1为变形后梁跨中竖向位移；Δ2为变形后撑杆下部端点的竖向位移.则撑杆在荷载作用的轴向变形δ为

δ=Δ1-Δ2

(1)

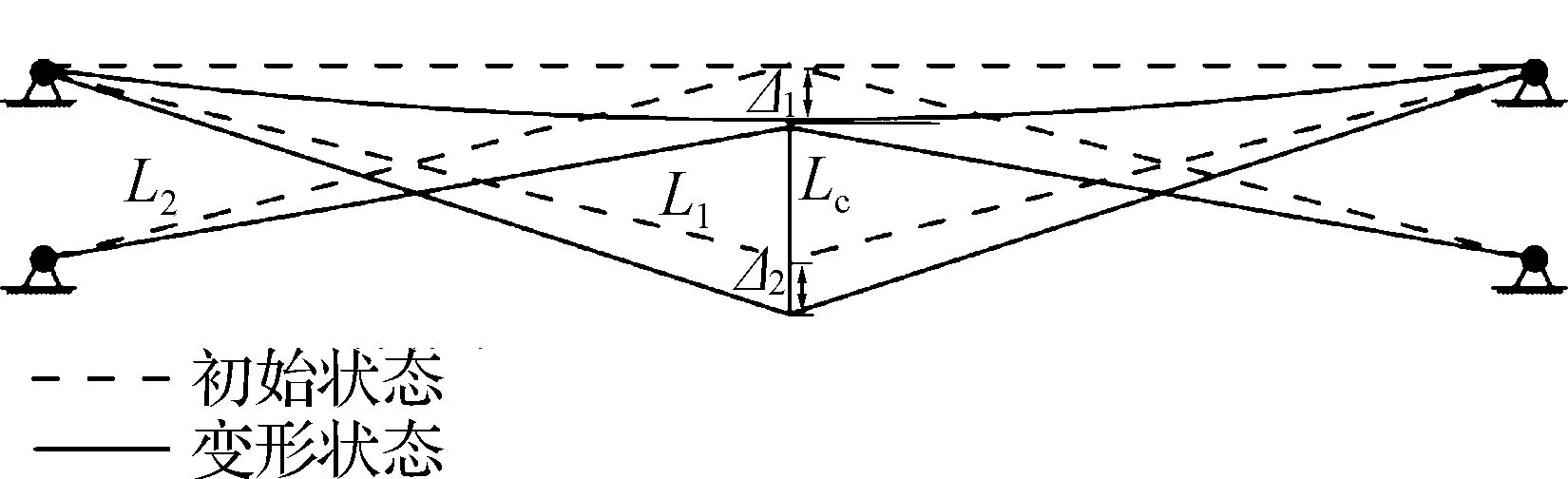
图5 二维单撑杆结构变形前后状态

当撑杆发生竖向位移时，谷索伸长而脊索缩短.在如图6所示的索杆结构变形原理图中，谷索与撑杆的初始夹角为α1，脊索与撑杆的初始夹角为α2，谷索与脊索变形后发生的转动角度分别为θ1和θ2，相应的伸长和缩短量分别为ΔL1和ΔL2.变形分析中，由于撑杆下部端点的竖向位移远小于谷索的初始长度(即Δ2≪L1),谷索的转动角度θ1近似为零，则撑杆下部端点的竖向位移Δ2可表示为

(2)

同理，梁跨中竖向位移为Δ1可表示为

(3)

(a) 谷索

(b) 脊索

将脊索的物理方程代入式(3)，则梁跨中竖向位移Δ1可表示为

(4)

式中，Δσ2为脊索变形前后的应力变化值；E为拉索材料的弹性模量.

根据图3的分析可知，撑杆的轴向变形δ相对于梁跨中竖向位移很小.将谷索的物理方程代入式(2)，并结合式(1)，则梁跨中竖向位移Δ1亦可表示为

(5)

式中，Δσ1为谷索变形前后的应力变化值.

根据式(4)计算出不同荷载状态下梁跨中竖向位移的计算值，并与图4中有限元分析得到的实际位移值进行比较，结果见表1.由表可知，梁跨中竖向位移的计算值与实际值误差均小于2.0%，精度高，可以满足雷达结构的功能需求，且荷载作用较小时精度更高.同理，若撑杆变形较小，将谷索应力变化值代入式(5)，计算得到的梁跨中竖向位移的精度亦满足需求.

表1 梁跨中竖向位移计算值与实际值对比

2.2 调控方法

根据索力与梁跨中竖向位移的关系，可通过监测索力进行主动控制设计.作动器布置于与梁相连的撑杆处，通过撑杆伸缩调整控制梁的变形.根据功能要求设定梁跨中竖向位移限值，确定相应的索力阈值.在逐级增加的荷载作用下，当梁跨中竖向位移在限值范围内，即相应索力未变化至阈值范围外时，负责补偿位移的撑杆作动器不启动，仅依靠结构自身的结构刚度支撑荷载作用.当外荷载继续增大时，索力将超出计算的阈值范围，作动器启动，调整撑杆伸缩.

根据图2所示的二维单撑杆结构进行主动控制分析.将脊索索力作为监测指标，假定梁跨中的竖向位移限值为±3.0 mm，代入式(4)可计算得到脊索索力的最大变化量为64.45 MPa, 得出脊索索力在正向和反向荷载作用下的阈值分别为49.4 和176.3 MPa.具体的控制思路为:监测脊索索力变化，若脊索索力减小，则表明施加的荷载为正向荷载.将脊索索力49.4 MPa作为控制限值，当索力未降低到49.4 MPa时，不启动作动器；当索力低于49.4 MPa时，撑杆作动器启动并伸长撑杆，从而维持脊索索力始终高于49.4 MPa.反之，若脊索索力增大，则表明施加的荷载为反向荷载.以脊索索力176.3 MPa为控制标准，当索力未超过176.3 MPa时，不启动作动器；当索力超过176.3 MPa时，撑杆作动器启动并缩短撑杆，从而维持脊索索力始终低于176.3 MPa.

采用主动控制设计后，不同荷载工况下谷索与脊索的索力变化见图7.由于需保证拉索不松弛，反向荷载时索力调控范围较为有限.主动控制设计将脊索索力维持在阈值内，则梁跨中竖向位移不会超过限值.当正向荷载小于1.50 N/mm或反向荷载小于1.56 N/mm时，梁跨中竖向位移处于限值范围内，撑杆作动器不启动.当正向荷载大于1.5 N/mm时，随着荷载作用的增大，撑杆需要的主动伸长量显著增大.当荷载为2.5 N/mm时，采用主动调控前后结构的变形云图见图8.由图可知，未调

(a) 谷索与脊索索力变化

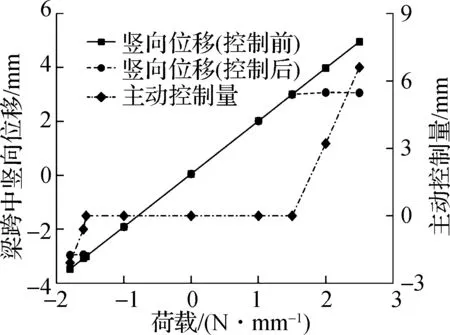
(b) 主动控制量和梁跨中竖向位移

(a) 控制前

(b) 控制后

控时脊索应力为10.4 MPa，梁跨中竖向位移为4.90 mm，撑杆主动伸长6.6 mm，脊索应力提升至49.4 MPa，梁跨中的竖向位移降低到3.01 mm.当反向荷载的数值大于1.56 N/mm时，亦需要通过缩短撑杆控制位移.当荷载为-1.80 N/mm时，梁跨中竖向位移为-3.48 mm，撑杆主动缩短2.09 mm，脊索应力提升至176.9 MPa，梁跨中的竖向位移降低到-2.96 mm.

3 索杆式雷达结构型面精度调控

取图1所示的索杆式雷达结构的中间跨平面鱼腹式梁结构和整体结构分别进行主动控制分析.对于平面鱼腹式梁结构，以梁结构1.5 mm的相对变形作为结构的主动控制限值.对于空间鱼腹式索杆雷达结构，考虑实际的风荷载作用，功能需求的型面精度RMSE不超过0.5 mm.其中，阵面面板的型面精度RMSE的计算方法为，提取荷载作用下阵面面板上均匀分布特征点的空间坐标，采用最小二乘法构建变形后阵面面板的拟合平面，计算变形后阵面面板上均匀分布特征点到拟合平面距离的均方根，即

(6)

式中，pi为单点相对位移值；n为阵面面板上均匀分布的特征点数量.

3.1 平面鱼腹式梁结构

平面鱼腹式梁结构如图9所示，跨度为1.5 m，由4根撑杆、1根梁和2条拉索组成.拉索两端固支，梁与撑杆上部端点连接，梁两端无额外约束.4根撑杆分别布置在沿梁长度方向的0.050、0.467、0.983、1.450 m处，其中，中间2根撑杆长0.12 m，两侧撑杆长0.09 m.拉索被撑杆分割成五跨(见图9).梁、撑杆、拉索的材料和截面参数与2.1.1节一致.拉索的初始预应力为113.02 MPa，梁承受竖直的均布荷载作用，跨中相对于两端的相对变形限值为±1.5 mm.采用跨②处脊索索力变化作为主动调控的输入信号，正向和反向均布荷载作用下脊索应力的阈值分别为94.0和136.0 MPa，在中间撑杆处布置作用器，控制撑杆的伸缩.

图9 平面鱼腹式梁结构

主动调控系统的执行过程如下：监测脊索索力变化，当索力减小时表明承受正向荷载作用，索力增大时表明承受负向荷载作用.若脊索索力未超过阈值，中间撑杆处的作动器不启动.若脊索索力小于正向荷载作用下的阈值，作动器驱动中间撑杆伸长；若脊索索力大于反向荷载作用下的阈值，作动器驱动撑杆缩短，从而维持脊索索力在调整范围内，保证梁相对变形不超过1.5 mm.

图10给出了不同工况下平面鱼腹式梁结构跨②处拉索的索力、最大相对位移与主动控制量.由图可知，拉索的索力变化与外荷载变化基本成线性关系.当正向荷载大于0.22 N/mm或者反向荷载大于0.30 N/mm时，荷载脊索索力超过限值，通过主动控制撑杆，将索力维持在阈值范围内，从而控制结构的最大相对位移在1.5 mm之内.主动调控后，谷索索力随着正向荷载的增大而增大，随着反向荷载的增大而减小.

(a) 谷索与脊索索力变化

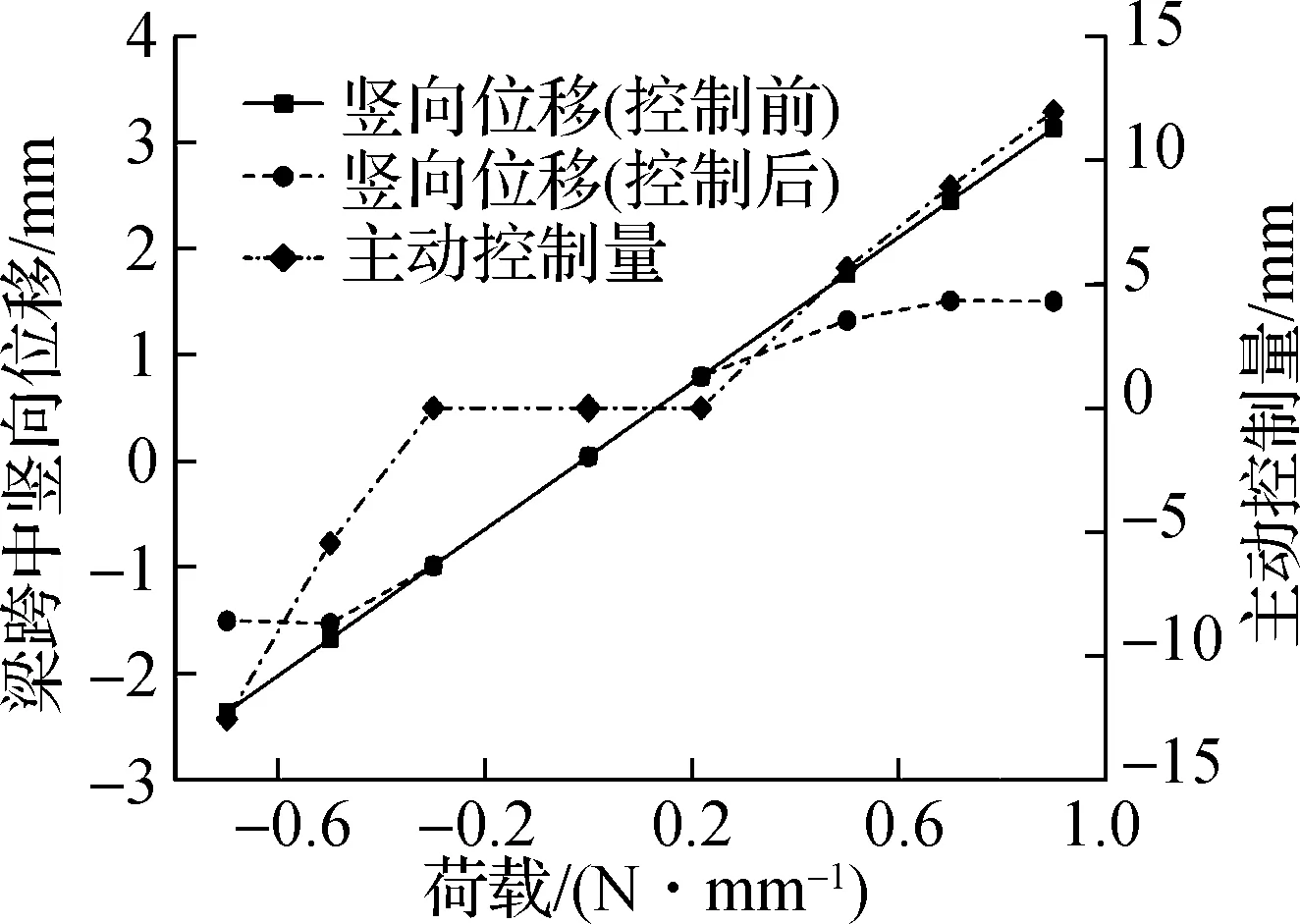
(b) 主动控制量和梁跨中竖向位移

图11为结构在正向0.9 N/mm荷载下主动控制前后结构变形情况.由图可知，主动调控前，梁的相对变形达到3.13 mm，中间撑杆主动伸长11.95 mm，梁的相对变形显著减小到1.50 mm.

3.2 空间鱼腹索杆式支承结构

对图1所示的空间鱼腹索杆式支撑结构进行有限元分析.面板尺寸为1.5 m×1.5 m，面板材质为铝合金，厚度为15 mm，撑杆与拉索采用2.1.1节所述的材料与截面，脊索和谷索的初始预应力分

(a) 控制前

(b) 控制后

别为107.9 和123.1 MPa.周边环梁采用Q235钢材，采用截面直径为40 mm、壁厚5 mm的圆管，结构四角固支约束.作动器布置于中间4根中间撑杆处.采用8级风(对应风荷载为0.23 kN/m2)、10级风(对应风荷载为0.56 kN/m2)和12级风(对应风荷载为0.95 kN/m2)分别进行计算分析，且均考虑风吸和风压2种类型，共计6种工况.

设定阵面面板型面精度RMSE限值为0.5 mm，设定图1中中间撑杆与边部撑杆之间的脊索为信号脊索，监测信号脊索的索力，计算信号脊索在风压和风吸荷载作用下索力的阈值分别为112和134 MPa.在风压作用下，信号脊索索力下降，若监测索力超过阈值，通过作动器驱动撑杆伸缩以补偿阵面面板的型面精度.图12展示了不同工况下空间鱼腹式索杆支承结构中信号脊索的索力值、阵面面板RMSE和主动控制量.

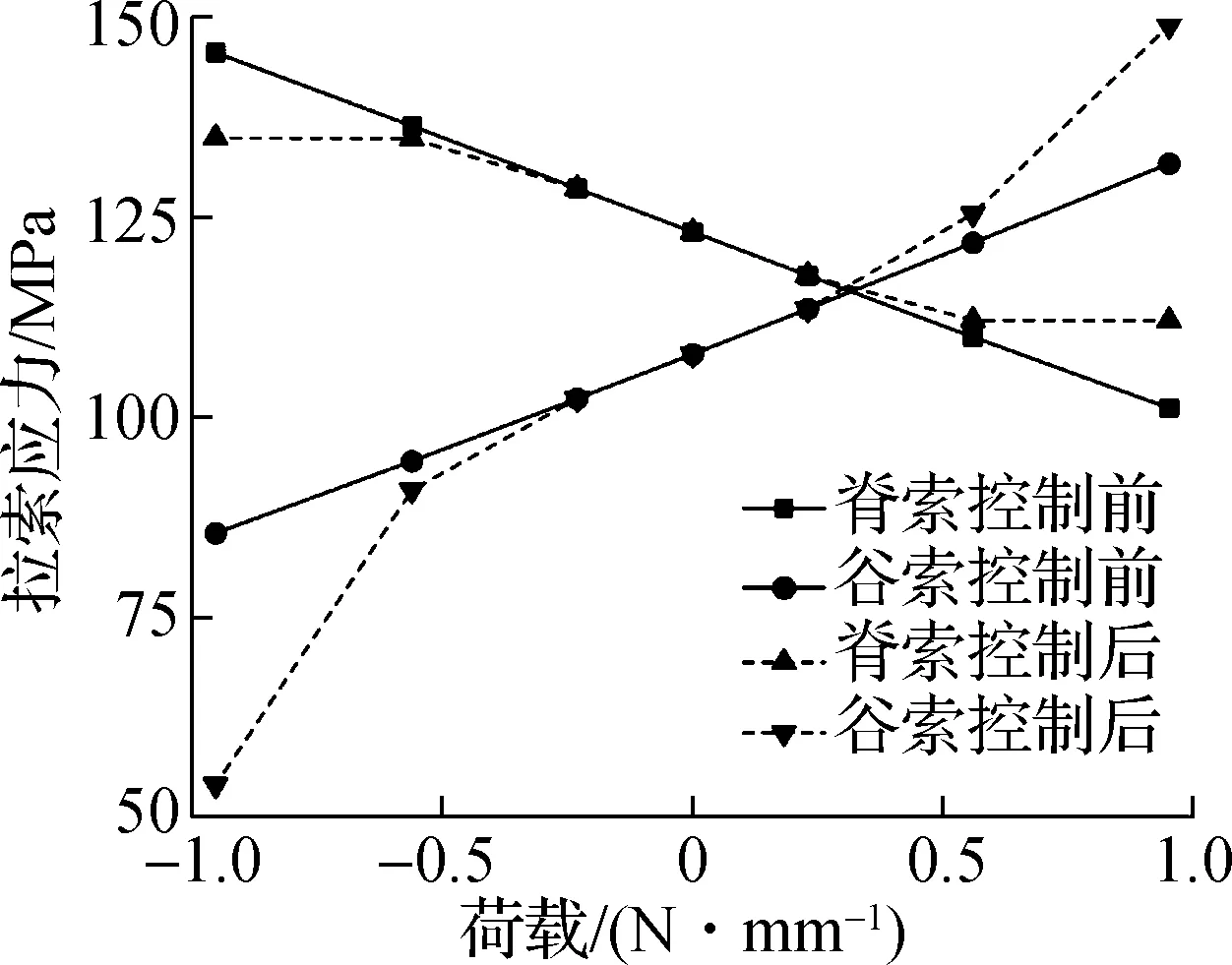
(a) 谷索与脊索索力变化

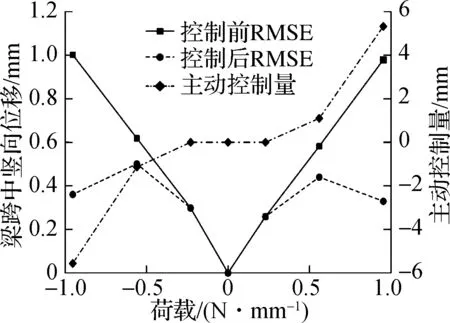
(b) 主动控制量和对应的RMSE

由图12(a)可知，通过主动控制将脊索索力维持在阈值以下.在8级风压和风吸荷载作用下，阵面面板的型面精度RMSE分别为0.259和0.298 mm，风吸荷载对阵面面板的型面精度较风压荷载更为不利，但是满足雷达结构的设计需求，无需进行主动调控.在10级风压和风吸荷载作用下，阵面面板的型面精度RMSE分别为0.582 和0.619 mm，对应的脊索索力超出限制，撑杆对应伸长1.10 mm和缩短1.13 mm，型面精度满足设计需求.在12级风压和风吸荷载作用下，阵面面板的型面精度RMSE分别为0.979和1.002 mm，主动调控下撑杆对应伸长5.33 mm和缩短5.56 mm，型面精度调控后分别为0.329和0.360 mm，满足功能需求.图13为12级风压荷载下空间鱼腹索杆式支承结构主动控制前后阵面面板变形情况.由图可知，在12级风载下，面板最大变形位于面板中心处，主动控制系统启动后，由整体变形转换为局部变形，可以显著提升阵面面板的型面精度.