氯离子侵蚀混凝土及细观参数影响的近场动力学模拟

2021-02-22李万金

东南大学学报（自然科学版） 2021年1期

李万金郭力周鑫洪俊

(东南大学江苏省高校工程力学分析重点实验室, 南京 210096)

大量研究表明,钢筋锈蚀破坏是混凝土破坏的主要原因,而氯离子侵蚀又是造成钢筋锈蚀的主要因素.同时,混凝土的各材料相有着不同的扩散特性,如骨料几乎不可渗透,会阻碍氯离子扩散；而界面过渡区(ITZ)由于高孔隙率会加速氯离子扩散.因此,研究混凝土中氯离子扩散过程和混凝土细观结构对其影响至关重要.

由于混凝土的非均质多相特性,采用解析方法处理细观尺度上氯离子扩散较为困难,而数值模拟是一种可行的方法.常用的数值方法主要有有限差分法、有限元法和无网格法等.如Ruan等[1]基于元胞自动机(cellular automata)方法建立氯离子扩散细观模型,并采用有限差分法求解该模型,较好地提高了细观模型计算效率.Guo等[2]建立了氯离子扩散有限元细观模型,研究发现,氯离子扩散过程高度依赖ITZ性能和骨料含量.Peng等[3]建立了五相细观模型,研究了氯离子扩散系数、损伤区域长度和宽度等参数对氯离子扩散过程的影响.avija等[4]建立了氯离子扩散的三维细观格构模型,研究了裂纹对氯离子扩散过程的影响.以上经典局部方法能够较好地研究细观尺度上的氯离子扩散过程,但往往不能捕捉到混凝土非均质性导致的非局部效应.

Silling[5]提出一种非局部方法,即近场动力学方法(peridynamics).该方法采用空间积分形式的控制方程,能够较好地处理不连续(如裂纹、界面等)问题和含非局部效应的问题[6-8].考虑到该方法的优势,Bobaru等[9]将近场动力学方法引入热传导研究,采用温度的积分代替温度的空间导数,建立了相应的控制方程.另外,Jabakhanji等[10]采用近场动力学研究渗流过程.Wang等[11]和王彩云等[12]采用态型近场动力学分别研究了岩石和混凝土的热力耦合变形破坏过程.氯离子扩散的控制方程与热传导和水分渗流的控制方程相类似,因此,可将近场动力学引入氯离子扩散过程的研究.

基于已有研究,本文建立了混凝土中氯离子扩散的细观近场动力学模型.通过与有限元模型计算结果的对比,对模型进行了验证；并在此基础上,讨论了骨料分布、骨料体积分数、骨料级配、ITZ厚度和ITZ扩散系数等细观参数对氯离子扩散过程的影响.

1 氯离子扩散的近场动力学细观模型

1.1 混凝土细观结构

混凝土是一种非均质材料,其细观结构复杂.混凝土的各相材料有着不同的扩散特性,因此,混凝土的宏观扩散性能与其细观结构有着密切的关系.本文中,假设混凝土是三相非均质材料,包括砂浆、骨料及两者之间的ITZ.类似于文献[7],将骨料假设为圆形,被ITZ包裹着,且随机分布于模型中.细骨料、水泥净浆和其他成分(如孔洞、裂纹等)组成砂浆.在细观尺度,假设砂浆为均质组分,其扩散特性与水灰比、孔隙率等因素相关.

混凝土中,骨料的体积分数高达70%,而粗骨料的体积分数约为40%.本文采用简化的四粒径段的骨料级配,其中粒径小于2.36 mm的骨料被认为是砂浆的一部分.粒径范围为2.36～4.75,4.75～9.50,9.50～12.70,12.70～19.00 mm的骨料体积分数分别为10%,51%,36%,3%.采用“生成-投放”方法[7]投放骨料,骨料既不与模型边界重叠,也不相互重叠,且不会影响ITZ的厚度和质量.ITZ是骨料与砂浆之间的薄界面层,该区域存在大量的可溶性氢氧化钙,因此ITZ是混凝土材料的“薄弱区”,对混凝土的输运性能影响较大.国内外学者对ITZ的厚度和输运性能进行了大量研究,Wang等[13]归纳了部分研究结果后发现,ITZ与砂浆的扩散系数之比均小于16.2,且大多数情况下,其比值小于10；ITZ的厚度为20～100 μm.

1.2 氯离子扩散理论

氯离子扩散是指溶液中氯离子在浓度梯度作用下发生的定向迁移,包括稳态扩散和非稳态扩散.单位时间内通过垂直于扩散方向参考平面的物质的量称为离子的扩散通量.对于一维情况下的稳态扩散,扩散通量J与浓度梯度∂C/∂x间的关系可用Fick第一定律来描述,即

(1)

式中,D为氯离子扩散系数；C为氯离子质量浓度；x为扩散深度.

实际情况下,氯离子的扩散通量J是一个随时间和空间变化的函数,对应体系的扩散过程为非稳态扩散过程.假设氯离子只在x方向扩散,即离子浓度在y和z方向上保持不变,只在x方向上有所变化.如图1所示,阴影截面为等浓度面,在x′和x处的质量浓度分别为Cx′和Cx,且Cx′>Cx.将2个阴影截面所围的区域作为研究对象,则左右两个阴影面积中流进和流出的离子通量之差ΔJ在数值上等于该区域内离子总量变化率(∂C/∂t)dx,即

图1 浓度梯度作用下氯离子扩散过程示意图

(2)

式中,t为扩散时间.将式(1)代入式(2),可得用于描述一维氯离子扩散过程的Fick第二定律：

(3a)

对于三维扩散问题,相应的扩散方程为

(3b)

式中,div()为矢量函数的散度算子；grad()为标量函数的梯度算子.

一维情况下,若式(3a)的初始条件和边界条件为

(4)

则可得到式(3a)的解析解为

(5)

1.3 近场动力学模型的建立

近场动力学是一种非局部理论,其假设物体由若干具有相应体积和质量的材料点组成.对于任意材料点x,它与周围一定圆形区域内的其他材料点发生作用.该半径为δ的圆形区域称为近场域,而材料点间的相互作用称为键.当近场域尺寸趋向于0,材料点间的相互作用变成局部作用,近场动力学方法退化为经典局部方法.本文采用氯离子浓度的积分代替经典局部模型中的浓度空间微分,建立了氯离子扩散近场动力学模型.该模型中,键类似于输送管道,将氯离子从一个材料点输运到另一个材料点.同时,键之间是相互孤立的,即键之间不发生氯离子输运.

假设图1中2个阴影截面所围的区域内平均离子质量浓度为Ca,则其离子总量变化率为

(6)

而离子通量差为

(7)

联立式(2)、(6)、(7)可得

(8)

将式(8)改写为近场动力学形式,可得

(9)

式中,Ca(x,x′,t)为键xx′中的平均氯离子质量浓度；K(x,x′)=K(x′,x)为键的扩散系数,可通过材料的扩散系数D求得.将式(9)左右两边同时除以||x′-x||,并以材料点x的近场域(Hx)为积分区域,对x积分,可得

(10)

假设与点x相连的所有键中的平均氯离子质量浓度与点x的氯离子质量浓度存在以下关系：

(11)

则可得

(12)

式中,VHx为点x的近场域体积.联立式(10)和(12),可得一维氯离子输运过程近场动力学模型的控制方程，即

(13a)

采用面积积分替代式(13a)中的线积分,则模型可推广到二维情况,即

(13b)

式中,k(x,x′)=K(x,x′)/VHx为键xx′的微扩散系数,其与混凝土各材料相的扩散系数之间的关系如下：

(14)

式中,Dbond=2DxDx′/(Dx+Dx′)，为键xx′的扩散系数,Dx和Dx′分别为材料点x和x′的扩散系数；ξ为键长.

1.4 数值离散

1.4.1 方程离散和迭代格式

采用均匀网格(网格间隔为Δx)离散二维模型,则式(13b)可离散成

(15)

式中,求和符号针对材料点xi近场域内的所有材料点xp；Aip为点xp所属区域被点xi近场域覆盖部分的面积.位于近场域边界处的材料点可能只有部分面积在近场域内,如果面积仍取为(Δx)2则会引发较大的数值误差,因此采用下式来提高计算的准确性[14]：

Aip=γ(Δx)2

(16)

式中,ξip为键xixp的键长.对于只被近场域部分覆盖的材料点,被覆盖部分的重心不再是其所属面积的中心点,因此采用下式修正键长：

(17)

当p=i时,式(15)右侧出现“零除零”的情况,无法直接求解；而p=i的情况是真实存在的,其在物理上表示存储在点xi所属区域内的氯离子浓度.因此,采用其相邻的8个材料点的平均值来近似求取,即

(18)

时间步迭代采用向前差分格式,即当前时间步在点xi处的氯离子浓度的时间导数由式(15)和式(18)求得；下一个时间步的氯离子浓度由下式求得：

(19)

式中,Δt为时间步长.采用向前差分方法处理时间积分在数值上是条件稳定的,因此有必要确定数值稳定条件来约束时间步长,从而防止引入数值误差.此处采用冯·诺依曼稳定性分析方法推导了数值稳定条件,即

(20)

采用自编MATLAB程序计算,式(19)可改写为矩阵格式：

Cn+1=Cn+ΔtKdCn=(I+ΔtKd)Cn

(21)

(22a)

(22b)

1.4.2 非局部Dirichlet(浓度)边界条件

近场动力学理论的边界条件与经典局部理论的边界条件有些许差异,这主要是由于近场动力学理论的非局部特性,会导致发生边界效应.非局部浓度边界条件需要施加在有限厚度的边界层上,而不是模型的表面.该边界层的厚度往往取为模型的近场域尺寸δ,而近场域尺寸一般取为3～5倍的材料点边长(Δx)较为合理,既能保证计算精度,又能保证计算效率[9].本文中,选取δ=5Δx.因此,在建模时,需要在原边界处增加厚度为δ=5Δx的虚拟边界层,用来施加浓度边界条件.

2 模型验证

采用氯离子扩散近场动力学细观模型和有限元细观模型来计算混凝土板中氯离子扩散过程,对比两者计算结果的一致性,来验证本文所建立模型的可行性.如图2所示,混凝土板尺寸为60 mm×60 mm,上边界暴露在氯离子环境中,其他3个边界是通量为0的密封边界.混凝土板的初始氯离子质量浓度为0；上边界的氯离子质量浓度为4.86×10-6g/mm3；扩散时间为200 d(1.728×107s).该模型采用四粒径段骨料级配,粒径段2.36～4.75,4.75～9.50,9.50～12.70,12.70～19.00 mm的体积分别占骨料总体积的10%,51%,36%,3%；骨料的体积分数为38.68%.ITZ的厚度和体积分数分别为50 μm和1.24%.骨料、砂浆和ITZ的氯离子扩散系数分别为0,9.125和91.25 μm2/s.

图2 混凝土细观模型的几何尺寸和边界条件(单位：mm)

近场动力学模型和有限元模型分别记作P1和F1.近场动力学细观模型P1采用MATLAB自编程序求解,其参数如下：材料点边长Δx=50 μm,近场域δ=5Δx=250 μm,虚拟边界层厚度δ=250 μm,材料点数为1.446×106,时间步长为50 s.对于有限元模型F1,采用商用有限元软件ABAQUS中的热传导模块来求解氯离子扩散过程.将热传导模型中的密度和比热容设为1,则热传导控制方程可转化为氯离子扩散控制方程.有限元细观模型的参数如下：采用4节点线性热传导四边形单元(DC2D4),单元边长Δx=50 μm,单元数为1.44×106,初始时间步长为50 s.

图3给出了t=200 d时刻的近场动力学模型和有限元模型中氯离子质量浓度分布云图.由图可看出,2种模型中氯离子扩散深度和浓度分布情况基本相同.图4给出了近场动力学模型和有限元模型中x=15,30,45 mm处氯离子质量浓度沿y轴方向分布的对比图(扩散时间为200 d)；其中骨料处的氯离子质量浓度为0,对应的值在曲线中予以省略.由图可看出,2种模型中氯离子质量浓度沿y轴方向分布基本相同,这也证明了氯离子扩散近场动力学细观模型的可行性.

(a) 模型P1

(b) 模型F1

图4 近场动力学模型和有限元模型中氯离子质量浓度沿y轴方向分布的对比图(t=200 d)

3 参数研究

为了明确混凝土细观结构和各材料相输运性能对混凝土中氯离子扩散过程的影响,本节对以下几个参数进行了研究：骨料分布、骨料体积、骨料级配、ITZ厚度和ITZ扩散系数.

3.1 骨料分布

采用3种不同的骨料分布(仅骨料分布位置不同,其他参数均相同)研究其对氯离子扩散过程的影响,相应模型记为D1,D2和P1.三种模型的几何尺寸、边界条件、各材料相的体积分数和扩散系数均与第2节算例中的相应参数相同.

图5给出了模型D1和D2中扩散200 d时的氯离子质量浓度分布云图.由图5和图3(a)可看出,氯离子扩散深度基本相同,这说明了骨料分布对氯离子扩散过程基本没有影响.图6中氯离子沿扩散方向的质量浓度分布拟合图亦可说明这一结论(氯离子的不均匀分布使得不同模型间的定量对比困难,因而采用式(5)反演数据得到宏观拟合曲线).当扩散100 d时,3种氯离子质量浓度分布曲线基本重合,但仍有些许差别.这主要是因为骨料是随机分布的；当扩散时间较短时,氯离子碰到的骨料数目有差别,从而会对氯离子扩散速度造成一定的影响.而当扩散200 d时,氯离子扩散深度相对较大,遇到的骨料数目相一致,从而不会影响氯离子扩散速度.因此,对于实际结构,一般遭受氯离子侵蚀时间较久,可忽略骨料分布对氯离子输运过程的影响.

(a) 模型D1

(b) 模型D2

图6 不同骨料分布下的氯离子沿扩散方向的质量浓度分布拟合图

3.2 骨料体积分数

采用5种不同的骨料体积分数(20%,30%,40%,50%,60%)研究其对氯离子扩散过程的影响.均采用四粒径段的骨料级配,其对应的ITZ体积分数分别为0.69%,1.03%,1.24%,1.73%和2.05%；其他参数如几何尺寸、边界条件、各材料相的扩散系数均相同,且与第2节算例中的对应参数相同.

图7给出了骨料体积分数与根据式(5)拟合的氯离子扩散系数的关系图.由图可看出,当骨料体积分数从20%增加到50%时,氯离子扩散系数逐渐减小；而骨料体积分数从50%提高到60%时,氯离子扩散系数略有增加.这主要是因为骨料和ITZ对氯离子扩散具有截然相反的影响；骨料会阻碍氯离子的扩散,而ITZ由于孔隙率大会加速氯离子的扩散.当骨料体积分数较小时,ITZ的体积分数也较小,骨料的阻碍作用大于ITZ的加速作用,因此氯离子扩散系数随骨料体积分数的增大而减小.当骨料体积分数较高时,ITZ的体积分数也较高,甚至相邻的ITZ会相互联通,从而ITZ的加速作用会大于骨料的阻碍作用,因此氯离子扩散系数有所增大.

图7 骨料体积分数与宏观氯离子扩散系数关系图

3.3 骨料级配

为了研究骨料级配对氯离子扩散过程的影响,采用4种不同的骨料级配,相应模型记为G1,G2,G3和P1.模型P1采用四粒径段骨料级配,而G3采用三粒径段骨料级配,不包含12.70～12.90 mm的粒径段,且12.70～12.90 mm粒径段的体积平均分配到其他3个粒径段.采用同样的分配方法,获取模型G2(含二粒径段)和模型G1(含一粒径段)的骨料尺寸分布.模型G1,G2,G3和P1中,骨料的体积分数为38.68%,骨料尺寸分布如表1所示；ITZ体积分数分别为2.90%,2.05%,1.43%和1.24%；其他参数如几何尺寸、边界条件、各材料相的扩散系数均相同,且与第2节算例中的对应参数相同.

表1 4种骨料级配模型中的骨料尺寸分布

图8给出了3种骨料级配下(模型G1～G3)氯离子质量浓度分布云图.由图8和图3(a)可看出,不同骨料级配情况下的氯离子扩散前缘基本相同.由图9也可看出,不同骨料级配情况下氯离子沿扩散方向的浓度分布差别不大,且与骨料级配的骨料段数没有明显的相关度.出现这种现象的原因与3.1节中骨料体积分数影响情况相似,主要是因为骨料的阻碍作用与ITZ的促进作用.如模型G1中骨料个数多,阻碍作用较大,但ITZ体积分数也大,甚至相邻的ITZ联通起来,因此相较于模型G2和G3,模型G1的扩散速度更快.再如模型P1的骨料个数少,ITZ体积分数也随之减小,促进作用减小,但骨料的阻碍作用更小,因此相较于模型G2和G3,模型P1的扩散速度更快.

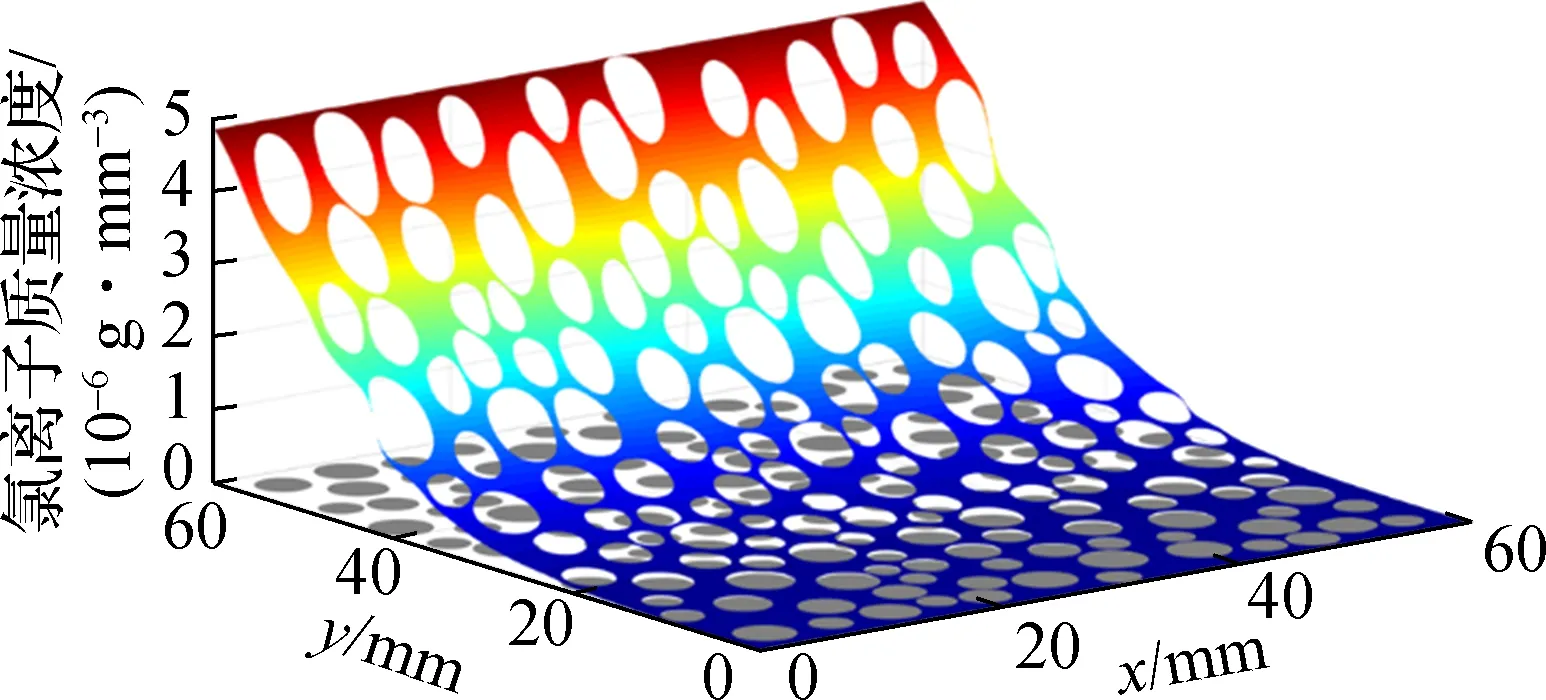
(a) 模型G1

(b) 模型G2

图9 不同骨料级配下氯离子沿扩散方向的质量浓度分布拟合图(t=200 d)

3.4 ITZ厚度

采用2种不同的ITZ厚度(50 和100 μm)研究其对氯离子输运过程的影响,相应模型记为P1和H1.两种模型的几何尺寸和边界条件、骨料体积分数、各相扩散系数均相同,且与第2节算例中的对应参数相同.

图10给出了模型H1(ITZ厚度为100 μm)中氯离子扩散200 d时的质量浓度分布云图.对比图10和图3(a)可看出,ITZ厚度为100 μm时氯离子扩散深度更大,这说明较厚的ITZ层会促进氯离子的扩散.图11给出了氯离子沿扩散方向的质量浓度分布的拟合曲线图.由图可清晰地看出,扩散100和200 d时,ITZ厚度为100 μm时的氯离子质量浓度均高于50 μm的情况.另外,扩散100 d时,ITZ厚度为50和100 μm的氯离子扩散系数分别为9.38和10.50 μm2/s；而扩散200 d时,则分别为8.64和8.82 μm2/s.

图10 模型H1(ITZ厚度为100 μm)的氯离子质量浓度分布云图(t=200 d)

图11 不同ITZ厚度下氯离子沿扩散方向的质量浓度分布拟合图(t=100,200 d)

3.5 ITZ扩散系数

采用5种不同的ITZ扩散系数DITZ(取砂浆扩散系数的1,3,5,7,10倍)研究其对氯离子输运过程的影响,相应模型记为n1,n2,n3,n4和P1.五种模型中,几何尺寸、边界条件、各材料相的体积分数均相同,且与第2节算例中相应的参数相同.

采用式(5)反演,得到模型n1,n2,n3,n4和P1的氯离子扩散系数分别为7.77,8.02,8.22,8.39,8.64 μm2/s；后4种情况下氯离子扩散系数分别是第1种情况的1.03,1.06,1.08和1.11倍.图12给出了不同ITZ扩散系数下氯离子沿扩散方向的质量浓度分布拟合图.由图也可看出,随着ITZ扩散系数的增加,氯离子扩散速度逐渐增加,但增加幅度不大,如ITZ扩散系数增大10倍,氯离子扩散速度增大11%.这主要是因为ITZ层太薄,体积分数仅为混凝土板的1.24%,仅增加ITZ扩散系数对氯离子扩散促进作用不大.