斜拉桥多索-浅拱-弹性约束模型及面内自由振动
2021-02-09苏潇阳康厚军皮梓豪丛云跃
苏潇阳 康厚军 皮梓豪 丛云跃
摘要:考虑斜拉桥的初始构型和支座刚度,建立了竖向弹性约束下的多索-浅拱动力学模型.首先基于索和浅拱的经典动力学方程,将浅拱在索-拱耦合处分段,推导了竖向弹性约束多索-浅拱的面内自由振动理论.然后采用分离变量法对其面内特征值问题进行了求解.同时以双索-浅拱模型为例,建立了相应的有限元模型,并将论文方法算出的频率和模态与有限元结果进行对比,从而验证了论文方法和模型的正确性.最后,对竖向弹性约束双索-浅拱的动力学特性进行了系统的参数化分析.结果表明:竖向刚度对系统的动力学特性有着明显的影响.
关键词:多索浅拱;动力学模型;弹性约束;自由振动;特征值
中图分类号:O343.9文献标志码:A
基金项目:国家自然科学基金资助项目(11972151,11872176),National Natural Science Foundation of China(11972151,11872176)
Elastically Constrained Multi-cable-stayed Shallow-arch Model in Cable-stayed Bridge and Its in-plane Free Vibration Research
SU Xiaoyang,KANG Houjun,PI Zihao,CONG Yunyue
(College of Civil Engineering,Hunan University,Changsha 410082,China)
Abstract:Considering the initial configuration and support stiffness of cable-stayed bridge,the multi-cablestayed shallow-arch model with vertical elastic constraints is established. Firstly,based on the classical dynamics e-quations of the cable and shallow arch,the theory of in-plane free vibration of the model is deduced by dividing the shallow arch into several segments at the cable-arch coupling points. Then,the double-cable-stayed shallow-arch model is taken as an example and its in-plane eigenvalue problem is solved by separation-of-variable method. At the same time,taking the double-cable-shallow arch model as an example,the corresponding finite element model is es-tablished. The frequencies and mode shapes calculated by the present method are compared with those obtained by fi-nite element method,which verifies the correctness of the method and model in this paper. Finally,a systematic para-metric analysis on the dynamics properties of the model is conducted. It is shown that the vertical stiffness has a sig-nificant effect on the dynamics properties of the system.
Key words:multi-cable-stayed shallow arch;dynamic model;elastic constraints;free vibration;eigenvalue
斜拉橋由于受力性能好、抗震性能强、造型优美及优越的跨越能力在大跨度桥梁中占有十分重要的地位.但由于斜拉桥跨度的不断增大以及新材料的不断应用,结构也变得更轻更柔,其动力学问题也就更为突出.因此,国内外学者对斜拉桥的动力学特性进行了大量研究. Gattulli等[1]通过经典变分公式,建立了斜拉桥索-梁结构横向动力学运动控制方程,并对其特征值问题进行了参数分析.本课题组[2-5]采用传递矩阵法对斜拉梁、双索梁结构的面内振动问题进行了详细的分析.通过考虑斜拉桥中桥塔的振动,提出了多梁离散弹簧动力学整体模型,并对斜拉桥的整体竖弯刚度进行了评估,探究了拉索对斜拉桥竖向振动频率的影响. Cao等[6]提出了由四根拉索和桥面梁组成的斜拉桥模型,并对该模型的线性特征值问题进行了深入的研究,该模型将桥面塔视为刚性,忽略了桥塔的振动.然而,在实际工程中,大跨度斜拉桥的桥面梁一般具有一定的预拱度以满足排水的需要,上述研究都没有考虑斜拉桥桥面梁的初始构型,这对理解斜拉桥的动力学行为难免有偏差.鉴于此,考虑桥面梁的初始构型,Kang等[7]建立了斜拉桥的双索-浅拱动力学模型,对端部轴向简谐激励下的1∶1∶1内共振动力学问题进行了研究.丛云跃等[8]基于索和浅拱的经典动力学方程,对双索浅拱的面内自由振动进行了研究.
以上研究均将斜拉桥的边界条件模拟为简支,实际上在基础变形以及由于基础变形所引起的附加惯性力的影响下,这可能会导致计算出的模型固有频率显著降低[9],尤其是低阶的频率.所以建立相应的弹性支承模型更符合实际工程情况.因此,国内外学者对弹性约束下各种模型的动力学特性进行了研究.易壮鹏等[10]研究了两端弹性约束浅拱的自由振动特性和非线性动力特性. Ding等[11]建立了带有非线性隔振的微曲梁的非线性动力学模型,研究了具有弹性边界的弯曲梁动力学问题,并推导了具有弹性边界的弯曲梁的模态函数和频率公式.
论文在上述研究的基础上,为建立更为精细的斜拉桥动力学模型,考虑斜拉桥桥面板的初始构型以及支座刚度的影响,建立两端竖向弹性支承的多索-浅拱动力学模型,并对该模型进行参数分析.论文模型相比于其他模型(例如索梁模型)更接近斜拉桥的真实状态,可以对斜拉桥的面内特征值问题进行分析,从而更准确地揭示斜拉桥的动力学特性.另外,基于该模型可以对斜拉桥的非线性振动进行研究,揭示斜拉索的大幅振动机理,为实际工程提供参考.
1两端弹性约束多索-浅拱模型
考虑支座处基础变形的影响,将模型两端支座简化为竖向弹性支承,论文暂不考虑支座处转动弹性支承[12].图1为考虑斜拉桥初始构型之后,两端竖向弹性约束的多索-浅拱模型,分别建立坐标系soy和xjojyj(j = 1,2,…,n)描述浅拱和索的振动,根据索的数量将浅拱分为i段,i=1,2,…,n+1.在能体现问题本质的前提下做出如下假设:




3数值分析
3.1模态分析
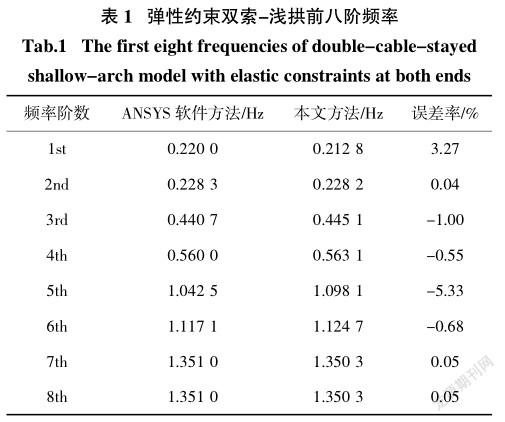
选取以下物理参数进行简要数值分析:浅拱弹性模量34.5 GPa,跨径300 m,截面惯性矩9.8 m4,单位长度质量4.4×104kg/m;斜拉索弹性模量210 GPa,长度115.5 m,单位长度质量10.4 kg/m,横截面积6.3×10-3m2,初始索力1 MN,拉索倾角30°.实际工程中支座的竖向刚度大概有7个数量级,因此选取两端弹性支座的无量纲刚度为k1= k2= 1 000.对应的实际刚度为1.25×107N/m.
为验证论文方法的正确性,利用有限元分析软件ANSYS15.0建立了相应的有限元模型.斜拉索采用Link1单元模拟,浅拱采用Beam3单元模拟,弹性支承采用Combine14单元模拟.表1和图2列出了根据论文方法和有限元模拟得到的结构前八阶频率和前五阶模态.可以看到,论文方法计算得到的结果和有限元模拟得到的结果吻合非常好,虽然第五阶频率的相对误差稍微有点大,但其绝对误差只有0.055 6(1.098 1~1.042 5).另外,仔细观察第五阶模态可以发现,索在有限元中只有拖动效应,而没有自身的振动,论文算法中体现出了索的自身振动和拖动效应,从而使索力加大,进而提高了结构的整体刚度,因此导致第五阶频率误差较大.
3.2参数分析
为研究基于该模型的斜拉桥更多动力学特性,采用论文中的计算方法对相关重要参数进行了分析.

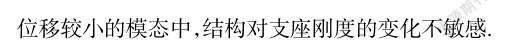
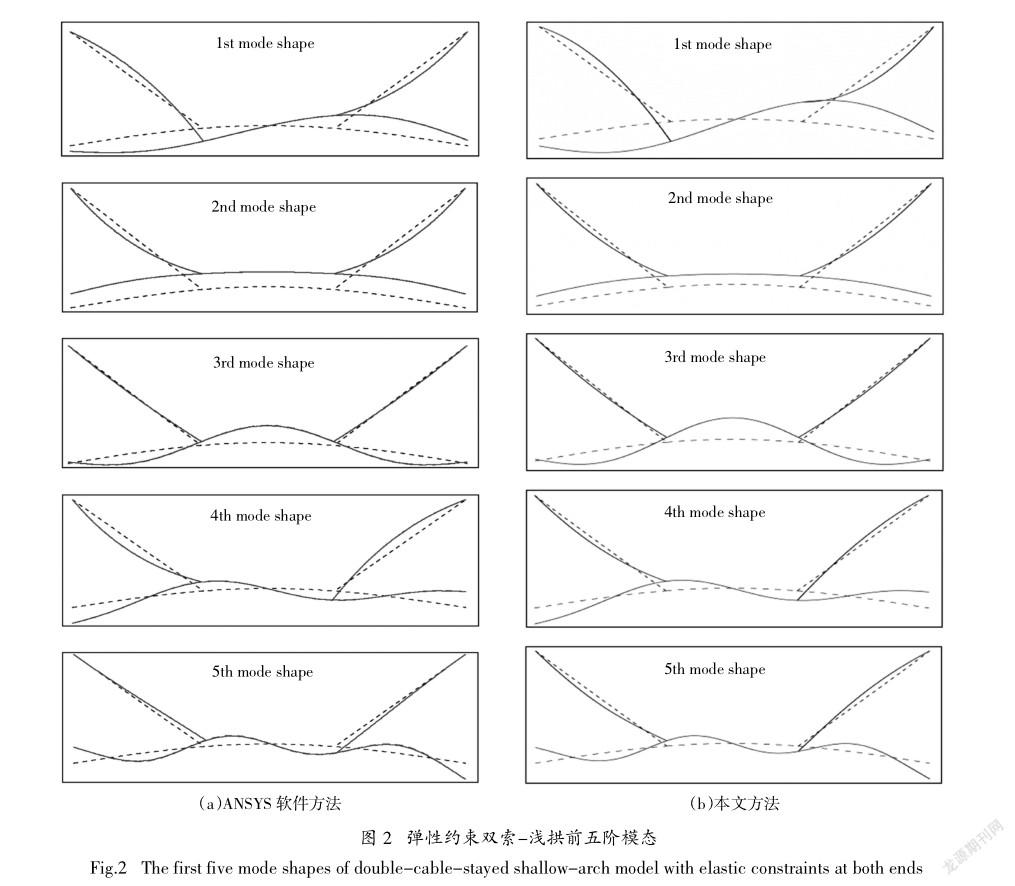
图4给出了k = 1 000和k = 10 000下模型的前五阶频率随浅拱矢跨比的变化曲线.从图中可以看出:在一定矢跨比范围内,某阶频率会随着矢跨比的增加而变大,随着矢跨比的继续增加,该阶频率将不再改变.论文称该影响范围为矢跨比对频率的影响域,随着支座弹簧刚度的变化,这个影响域也会随之发生变化.
另外,图4(a)中的前两阶频率,图4(b)中的前三阶频率之间分别出现了频率曲线相互靠近而又分离的现象,即veering现象,这与文献[8]中观察到的现象一致.然而,各阶频率对支座弹簧刚度的敏感程度不同,如图3所示,第一、三阶频率随支座刚度的增加变化较小,因此在图4(a)中,veering现象发生在前两阶频率之间,而在图4(b)中,veering现象发生在前三阶频率之间.仔细观察图4(a)可以发现,当f = 0.022 5时,ω2≈ω1;当f = 0.018 3时,ω3≈2ω2.这表明模型各阶频率之间存在多种内共振关系,此时相邻阶模态之间会发生能量传递和模态互换,并导致索的大幅振动,工程中应注意设计参数以避免此现象的发生.
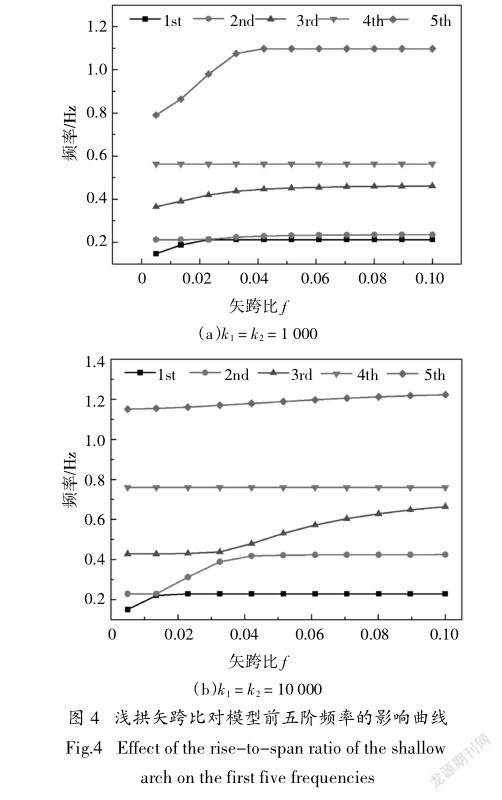
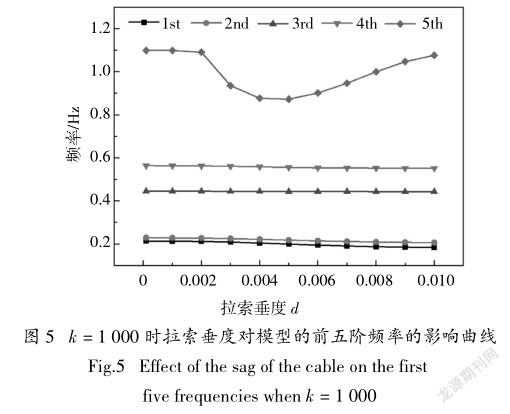
图5给出了拉索垂度對模型的前五阶频率的影响曲线.从图中可以看出前四阶模态频率随着拉索垂度的增加而缓慢减小,这是因为前四阶模态中拉索的振动主要由浅拱的拖动造成,随着拉索垂度的增加,拉索等效刚度减小,整体结构刚度也减小,从而频率减小.第五阶频率随着拉索垂度的增加先减小后增加,这是因为随着垂度的进一步增加,索与水平方向的夹角减小,索力的水平分量变大,从而导致浅拱的几何刚度增大,结构的频率增大.第五阶模态拉索自身振动幅度较大,因此拉索垂度对模型频率的影响也更加明显.
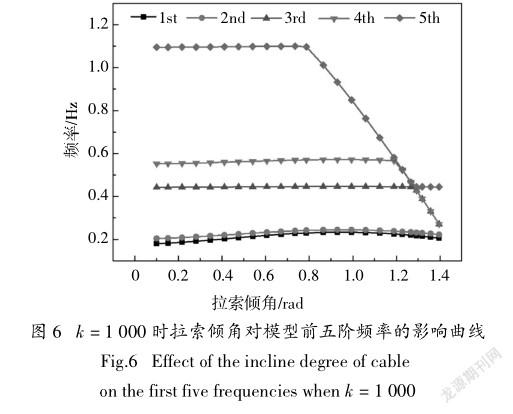
图6给出了拉索倾角对模型前五阶频率的影响曲线.从图中可以看出,前两阶频率随着拉索倾角的增加先缓慢增加,再缓慢下降,但总体来说变化幅度很小.当拉索倾角较小时,三、四、五阶频率随拉索倾角的增加变化不大,当拉索倾角继续增加到一定值时,频率会显著下降.这是因为随着倾角的增大,拉索两端锚固点水平距离不变,斜拉索变长,质量也随之增加,因此频率变小[14,15].另外,当拉索倾角增加到1.2左右时,第四阶和第五阶频率很接近,这是因为此时第四阶和第五阶模态都是索单独振动的局部模态,第四阶是反对称模态,第五阶是正对称模态;而当拉索倾角增加到1.3左右时,局部模态变为第三阶和第四阶,因此第三阶和第四阶的频率曲线发生了重合.
4结论
论文考虑斜拉桥的初始构型和更合理的支承条件,建立了竖向弹性约束下的多索-浅拱动力学模型.基于索和浅拱的经典动力学方程,将浅拱在索-拱耦合处分段,推导了竖向弹性约束多索-浅拱的面内自由振动理论.以竖向弹性约束双索-浅拱模型为例,对其面内特征值问题进行了求解,通过与有限元模拟得到的结果进行对比,表明论文方法和模型的正确性.最后,对模型的动力学特性进行了详细的参数化分析并由此得出如下结论:
1)随着弹性支座刚度的增加,结构的各阶频率增加,在支座位移大的模态中,频率对支座刚度变化更为敏感.支座刚度会影响系统内共振的发生从而影响系统的动力学行为,将两端边界条件视为弹性约束更合理.
2)增加浅拱矢跨比会使得结构的某阶频率明显增加,从而改变结构的内共振关系,在斜拉桥动力特性分析中应当考虑桥面梁初始构型所造成的影响.
3)改变浅拱矢跨比和拉索倾角会产生veering现象.支座刚度的变化会影响这一现象的出现,刚度越大该现象越明显.
4)拉索垂度对低阶频率影响不明显,对高阶频率的影响较为明显.拉索倾角对局部模态影响较大,因此在进行拉索设计时应该设计合适的倾角,避免局部模态出现在低阶模态而产生内共振.
参考文献
[1]GATTULLI V,MORANDINI M,PAOLONE A. A parametric ana-lytical model for non-linear dynamics in cable-stayed beam[J]. Earthquake Engineering & Structural Dynamics,2002,31(6):1281—1300.
[2]康厚军,解维东,郭铁丁. CFRP索斜拉梁面内自由振动建模及参数分析[J].湖南大学学报(自然科学版),2016,43(9):18—25. KANG H J,XIE W D,GUO T D. Modeling and parameters analysis on in-plane free vibration of cable-stayed beam[J]. Journal of Hu-nan University(Natural Sciences),2016,43(9):18—25.(In Chi-nese)
[3]龔平,苏潇阳,蔡向阳,等.拉索对斜拉桥竖向频率的影响研究[J].振动工程学报,2018,31(6):957—965. GONG P,SU X Y,CAI X Y,et al. The influence of cables on verti-cal frequency of cable-stayed bridge[J]. Journal of Vibration Engi-neering,2018,31(6):957—965.(In Chinese)
[4]SU X Y,KANG H J,GUO T D,et al. Dynamic analysis of the inplane free vibration of a multi-cable-stayed beam with transfer ma-trix method[J]. Archive of Applied Mechanics,2019,89(12):2431—2448.
[5]康厚军,苏潇阳,龚平,等.漂浮式独塔斜拉桥竖弯刚度评估新方法[J].湖南大学学报(自然科学版),2017,44(11):126—134. KANG H J,SU X Y,GONG P,et al. A new method for verticalbending stiffness evaluation of floating single-tower cable-stayed bridge[J]. Journal of Hunan University(Natural Sciences),2017,44(11):126—134.(In Chinese)
[6]CAO D Q,SONG M T,ZHU W D,et al. Modeling and analysis of the in-plane vibration of a complex cable-stayed bridge[J]. Journal of Sound and Vibration,2012,331(26):5685—5714.
[7]KANG H J,GUO T D,ZHAO Y Y,et al. Dynamic modeling and inplane 1:1:1 internal resonance analysis of cable-stayed bridge[J]. European Journal of Mechanics - A/Solids,2017,62:94—109.
[8]丛云跃,康厚军,苏潇阳. CFRP索斜拉桥的索-浅拱模型及面内自由振动分析[J].固体力学学报,2018,39(3):316—327. CONG Y Y,KANG H J,SU X Y. Cable-stayed shallow-arch model-ing and In-plane free vibration analysis of cable-stayed bridge with cfrp cables[J]. Chinese Journal of Solid Mechanics,2018,39(3):316—327.(In Chinese)
[9]MACBAIN J C,GENIN J. Natural frequencies of a beam considering support characteristics[J]. Journal of Sound and Vibration,1973,27(2):197—206.
[10]易壮鹏,康厚军,王连华.弹性支撑浅拱的非线性动力行为分析[J].动力学与控制学报,2013,11(2):142—148. YI Z P,KANG H J,WANG L H. Research on the nonlinear dynamic behaviors of elastic support shallow arch[J]. Journal of Dynamics and Control,2013,11(2):142—148.(In Chinese)
[11]DING H,CHEN L Q. Nonlinear vibration of a slightly curved beam with quasi -zero -stiffness isolators[J]. Nonlinear Dynamics,2019,95(3):2367—2382.
[12]李煬,谭霞,丁虎,等.两端带有弹簧支撑的轴向运动梁振动分析[J].动力学与控制学报,2019,17(4):335—340. LI Y,TAN X,DING H,et al. Nonlinear transverse vibration of an axially moving beam with vertical spring boundary[J]. Journal of Dynamics and Control,2019,17(4):335—340.(In Chinese)
[13]ZKAYA E,SARIGL M,BOYACI H. Nonlinear transverse vibra-tions of a slightly curved beam carrying a concentrated mass[J]. Acta Mechanica Sinica,2009,25(6):871—882.
[14]丛云跃,康厚军,郭铁丁,等. CFRP索斜拉桥面内自由振动的多索梁模型及模态分析[J].动力学与控制学报,2017,15(6):494—504. CONG Y Y,KANG H J,GUO T D,et al. A multiple cable-beam model and modal analysis on in-plane free vibration of cable-stayed bridge with cfrp cables[J]. Journal of Dynamics and Control,2017,15(6):494—504.(In Chinese)
[15]吕建根,王荣辉.索梁结构中抗弯刚度斜拉索的非线性响应[J].动力学与控制学报,2019,17(4):326—334. LJ G,WANG R H. Nonlinear response of stay cables with flexural rigidity in cable-stayed beams[J]. Journal of Dynamics and Con-trol,2019,17(4):326—334.(In Chinese)
