长期荷载作用下钢-混凝土组合梁的挠度计算与分析
2021-02-09冀伟孙斌白倩罗奎
冀伟 孙斌 白倩 罗奎
摘要:為科学合理计算钢-混组合梁在长期荷载作用下的挠度,综合考虑钢梁与混凝土桥面板层间滑移效应、钢-混组合梁全截面剪切变形及混凝土桥面板收缩徐变的影响,运用能量变分法推导出钢-混组合梁挠度计算的控制微分方程.引入均布荷载作用下简支和两跨连续钢-混组合梁的自然边界条件,求解出了钢-混组合梁在这两种边界条件下的挠度计算公式.计算公式的可靠性得到了实测值和有限元值的验证.研究结果表明:考虑剪切变形与层间滑移后,两跨连续钢-混组合梁跨中最大挠度计算值相对于初等梁理论增大37.4%,而同时考虑混凝土收缩徐变后其挠度计算值增大58%;简支钢-混组合梁考虑混凝土的收缩徐变后挠度计算值相对于初等梁理论增大1.55倍,可见混凝土的收缩徐变效应对钢-混组合梁的挠度影响较大.研究成果可为实际工程中钢-混组合梁在长期荷载作用下的挠度计算提供理论依据.
关键词:钢-混组合梁;收缩徐变;长期性能;层间滑移;挠度分析
中图分类号:U448.216文献标志码:A
基金项目:国家自然科学基金资助项目(51708269,51868039),National Natural Science Foundation of China(51708269,51868039);中国博士后科学基金资助项目(2018M643766),China Postdoctoral Science Foundation(2018M643766);兰州交通大学“百名青年优秀人才培养计划”基金资助项目
Calculation and Analysis of Deflection for Steel-concrete Composite Girder under Long-term Loads
JI Wei1,SUN Bin2,BAI Qian1,LUO Kui1
(1. College of Civil Engineering,Lanzhou Jiaotong University,Lanzhou 730070,China;2. Chongqing Railway Group Co Ltd,Chongqing 401120,China)
Abstract:In order to accurately calculate the deflection of steel-concrete composite girders under long-term loads,considering the shear deformation of composite girder,slip effect at the steel-concrete interface and shrinkage and creep of the concrete slab,the equilibrium differential equations for calculating the deflections of steel-concrete composite girder are derived by using the energy variational method. By introducing the boundary conditions on the simply supported and continuous composite girders under uniformly distributed load,the deflection calculation formu-las can be obtained. The reliability of the calculation formulas is verified by comparing the experimental results and the results of finite element analyses. The results show that maximum deflection of two-span continuous composite girder considering shear deformation and interlayer slip increases by 37.4% when compared with the results from pri-mary beam theory,and the deflection increases by 58% after considering the shrinkage and creep of concrete. The calculated maximum deflection of simply supported composite girder after considering the shrinkage and creep of con-crete is 1.55 times larger than that of the primary beam theory. It can be seen that shrinkage and creep can have a sig-nificant influence on the girder’s deflection. The research results can provide a theoretical basis for the deflection cal-culation of steel-concrete composite girders under the long-term loads.
Key words:steel-concrete composite girder;shrinkage and creep;long-term behavior;interfacial slip;deflec-tion analysis
钢-混凝土组合结构可以充分发挥混凝土与钢材各自的优点,即混凝土主要抗压,钢材主要抗拉,结构受力较为合理.钢-混凝土组合结构特别适用于装配式中等跨径桥梁及快速施工的桥梁[1].在实际工程中,钢与混凝土的连接常采用剪力连接件,剪力连接件的变形会引起钢梁与混凝土板的界面滑移,降低组合梁整体刚度,从而产生附加变形.此外,钢-混凝土组合梁在长期荷载作用下,由于混凝土收缩徐变的影响,其挠度会随时间增加而增大,而梁变形过大会影响其正常使用性能[2].
Dezi等[3-4]提出了考虑混凝土收缩徐变效应的钢-混凝土连续组合梁的时变分析方法. Cheng[5]以钢-混凝土组合T梁为例,分析了滑移和混凝土收缩徐变对其应力和挠度的影响. Cao等[6]对三根预应力钢-混凝土组合连续箱梁(无预应力、部分预应力和完全预应力)进行了420 d的长期荷载试验,提出了考虑持续荷载、收缩、徐变及预应力组合效应对钢-混凝土组合连续箱梁长期挠度的计算模型. Tong等[7]建立了考虑混凝土徐变、收缩和开裂的三维黏弹塑性损伤本构模型,研究了预应力钢-混凝土组合梁的短期和长期性能.项贻强等[8]在考虑体外预应力和混凝土长期性能对钢-混组合梁界面滑移影响的基础上,提出界面滑移时变的计算公式,并探讨了钢-混组合梁在混凝土长期效应作用下的滑移变化规律.肖岩等[9]在考虑界面滑移效应的基础上,提出了钢-混组合梁挠度计算的二阶算法,并求得4种不同边界条件下组合梁的挠度.冀伟等[10]在考虑钢梁与混凝土板的滑移效应和组合梁剪切变形的基础上,运用能量变分原理求得了钢-混凝土组合梁的挠度计算公式.褚少辉等[11]运用有限元分析研究了钢-混组合梁的滑移分布规律与特点. Nguyen等[12]提出可以考虑混凝土收缩、徐变和开裂之间相互作用的非线性时变特性钢-混组合梁有限元模型.
综上,国内外学者已对钢-混凝土组合梁的界面滑移效应和长期荷载效应进行了研究,但对同时考虑钢-混组合梁全截面剪切变形、钢-混接触面的滑移效应及混凝土长期效应下钢-混凝土组合梁的挠度计算还存在不足.因此,本文在综合考虑上述三种效应的基础上,运用能量变分原理建立了钢-混组合梁挠度计算的控制微分方程,引入梁弯曲角、剪应变和挠度的微分关系,按照给定的自然边界条件求得钢-混组合梁在长期荷载作用下挠度的计算公式.同时,钢-混凝土组合梁的高跨比对梁的剪切变形有影响,因组合梁属于薄壁构件,往往承担较大的荷载,其跨高比较小,将导致剪切影响系数较大,使剪切变形成为一个不可忽略的因素[13];文献[10]研究了混凝土与钢梁的界面连接对层间滑移的影响,在其他条件不变的情况下,抗剪刚度越小,层间滑移效应对挠度的影响越不可忽略,因此有必要在计算中对层间滑移与剪切变形两种效应予以综合考虑.本文基于以上条件,通过简支和两跨连续钢-混组合梁的实例验证了所得计算公式的正确性和适用性,研究成果可为实际工程中钢-混凝土组合梁在长期荷载效应下的挠度计算提供理论依据.
1钢-混凝土组合梁挠度计算的控制微分方程
1.1基本假定
运用能量变分原理对钢-混凝土组合梁的挠度进行分析时,引入以下基本假定[14-15]:
1)混凝土桥面板与钢梁的横截面均符合平截面假定,剪力连接件为等效的均匀连续弹性介质;
2)钢梁与混凝土在整个受力阶段的应力-应变关系为线性关系,混凝土在整个受力阶段未开裂、剥落;
3)忽略钢-混组合梁的掀起现象,不考虑其横向变形,混凝土桥面板与钢梁的曲率完全相等;
4)忽略桥面板剪力滞效应对钢-混组合梁挠度的影响.
1.2考虑层间滑移效应影响
假定层间滑移界面符合Goodman弹性夹层假设(如图1所示),ks为剪力连接件的抗剪刚度,实际工程中应根据混凝土标号、栓钉长短、间距、直径和抗剪切联接度等参数的影响对剪力连接件进行抗剪实验来确定实际抗剪刚度;Es、As与Ec、Ac分别为钢与混凝土材料的弹性模量和截面积.如图2所示的钢-混组合梁,hc、hs分别为混凝土板和钢梁各自截面中性轴到组合截面中性轴的距离,h为hc和hs之和;Hc、Hs分别为混凝土桥面板和钢梁截面的形心,H为钢-混组合梁截面的形心.在外力作用下的鋼-混组合梁,组合截面的弯曲变形和剪力连接件的剪切变形将产生层间相对滑移.图2中,εcs、εss分别为滑移效应引起的混凝土桥面板和钢板的应变,θ为组合梁的弯曲角.








4算例分析
4.1简支组合梁算例
选取文献[17]中的钢-混凝土组合实验梁试件LCB1及LCB2为研究对象,用于验证本文所得挠度计算公式的正确性. LCB1和LCB2试件中钢梁与混凝土翼板梁跨均为4 m,图9为LCB1和LCB2的截面示意图.钢梁材质为Q235b,弹性模量为2.1×105 MPa.试件LCB1翼板混凝土材料为C20,轴心抗压标准值fck= 20 MPa,龄期28 d弹性模量为3.18×104 MPa,试件LCB2翼板混凝土材料为C30,轴心抗压标准值fck= 30 MPa,龄期28 d弹性模量为3.47×104 MPa.文献[17]的简支试验梁是按完全抗剪连接设计的,即抗剪刚度趋于无穷,而滑移效应趋于0,本例假定抗剪刚度过大而忽略滑移位移.两试件均承受满跨均布荷载6.23 kN/m.

根据CEB-FIP(MC90)规范,采用Midas Civil有限元软件模拟在平均湿度为67%、构件理论厚度为54.5 mm下,C20与C30混凝土的徐变系数与收缩应变在加载1 000 d内的发展情况,如图10所示.有限元考虑收缩徐变框图和算法如图11所示.

采用有限元Midas Civil软件建立了试件LCB1、LCB2的有限元模型,由于在Midas有限元模型中采用双单元法刚性连接建模时,混凝土板部分在徐变作用下产生一定误差,因此,本文整体采用标准截面法(组合梁截面)建模.
本文根据静定结构的收缩和徐变引起结构的变形、超静定结构的收缩和徐变引起结构次内力进而引起结构变形的原理进行了收缩徐变的数值运算.在有限元计算中,收缩徐变只有与施工过程结合才有意义,桥梁结构分析中应分阶段,按施工顺序考虑收缩徐变效应,本文最终挠度计算结果为有限元模型挠度计算值叠加层间滑移挠度理论计算值.
Midas Civil实现混凝土的收缩和徐变一般分两个步骤:一是定义收缩、徐变系数;二是将定义的收缩徐变模式赋予材料.图12对应为简支梁试件LCB1、LCB2的计算模型,两试件区别在于混凝土的轴心抗压标准值和龄期28 d弹性模量值不同.通过建立试件LCB1的有限元模型并求解出对应的挠度值,然后改变模型组合梁截面中混凝土材料及相应的弹性模量,重新将定义的收缩徐变模式赋予混凝土材料,运算求解试件LCB2对应挠度值.模型中纵向划分为20个单元和21个节点,单元长度等分为0.2 m,约束布置以梁左端为固定铰支座,右端为活动铰支座,通过改变模型混凝土材料特性分析试件LCB1、LCB2挠度变化情况.
将理论公式计算的跨中挠度值与有限元值及实测值进行对比分析,对比结果见表1.


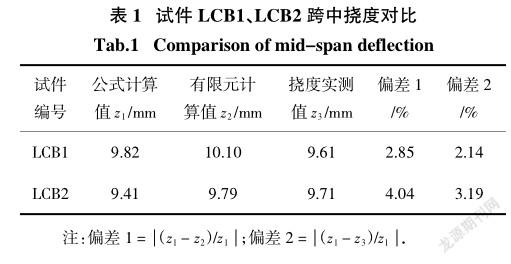
从表1中可以看出,理论公式计算的挠度值与有限元值及实测值的误差在5%以内,吻合较好,验证了所推导的钢-混组合梁计算公式的正确性.试件LCB1、LCB2加载500 d后的理论挠度计算结果,如图13所示.

由图13中可见,简支钢-混组合梁加载500 d后,试件LCB1收缩徐变后的挠度是瞬时挠度的2.55倍,试件LCB2收缩徐变后的挠度是瞬时挠度的2.49倍,可见混凝土的收缩徐变效应对挠度的影响较大.
4.2两跨连续组合梁算例
选取文献[3]中的两跨连续钢-混凝土组合梁试件进行长期荷载效应分析,梁跨为2×25 m,承受满跨均布荷载64.56 kN/m,其横截面尺寸如图14所示,抗剪刚度取值参考文献[18],取ks= 400 MPa.
采用Midas Civil 2018有限元软件建立了两跨连续钢-混组合梁桥的三维有限元模型,模型中纵向划分为26个单元和27个节点,其中单元长度为2 m,跨中处分割单元为1 m,约束布置以梁两端为活动铰支座,跨中为固定铰支座,如图15所示.


从表2中可知,本文理论公式计算的挠度值与有限元值吻合较好,验证了所推导的两跨连续钢-混组合梁挠度计算公式的正确性.为进一步验证本文理论公式的正确性,在考虑混凝土收缩徐变效应下将本文公式计算求得的中支点反力与文献[3]的中支点反力进行对比分析,二者吻合较好,如图16所示.
首先对比分析了两跨连续钢-混凝土组合梁在以下三种情况下的挠度:①初等梁理论(C)计算所得挠度;②初等梁理论(C)+考虑全截面剪切变形(Q)计算所得挠度;③初等梁理论(C)+考虑全截面剪切变形(Q)+考虑层间滑移(R)计算所得挠度,对比结果如图17所示.

從图17中可以看出,在初等梁理论基础上考虑层间滑移效应和剪切变形效应后,跨间最大挠度增长了37.4%,仅剪切变形效应引起的挠度增加了14.2%.可见,剪切变形效应和层间滑移效应对钢-混凝土连续梁挠度的影响不可忽略.
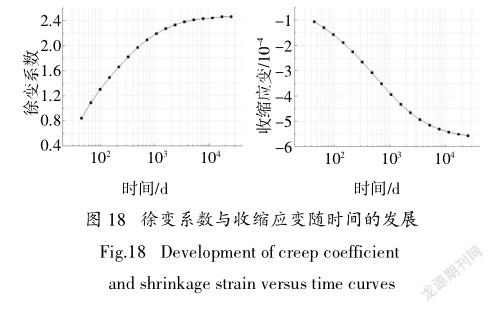
在图17情况③的基础上考虑混凝土收缩徐变效应对两跨连续钢-混组合梁挠度影响.从加载时刻算起,在混凝土收缩徐变时效期为70年,考虑周边环境相对湿度为50%,结构构件理论厚度为h = 184 mm,轴心抗压标准值30 MPa.混凝土板徐变系数与收缩应变发展按照CEP-FIP(MC90)的规定进行计算求得,如图18所示.采用本文所得的理论计算公式求得了两跨钢-混连续组合梁在加载70年后跨中挠度的发展情况,如图19所示.

从图19中可以看出,在初始时刻考虑剪切变形效应和层间滑移效应,组合梁经70年加载后,仅考虑混凝土徐变效应下产生的挠度是瞬时加载挠度的1.32倍,考虑混凝土收缩徐变效应产生的挠度是瞬时挠度的1.58倍.因此,混凝土长期荷载效应对两跨连续钢-混组合梁的挠度有较大影响,不可忽略.
5结论
本文对考虑钢-混组合梁剪切变形、层间滑移效应和混凝土桥面板收缩徐变效应下的钢-混凝土组合梁挠度进行计算与研究分析,所得结论如下:
1)本文推导所得长期荷载作用下钢-混凝土组合梁挠度计算公式的正确性得到有限元和实测值的验证,理论公式推导过程简单,物理意义明确,且能满足工程计算精度要求.
2)考虑混凝土收缩徐变后,简支钢-混组合梁跨中最大挠度比加载瞬时挠度增大1.55倍,可见混凝土的收缩徐变效应对简支钢-混组合梁挠度的影响较大.
3)考虑层间滑移效应和剪切变形效应,两跨连续钢-混组合梁最大挠度在初等梁理论基础上增长了37.4%,仅考虑剪切变形效应引起的挠度增加了14.2%.可见,剪切变形效应和层间滑移效应对钢-混连续梁挠度的影响不可忽略.
4)考虑剪切变形效应和层间滑移效应,两跨连续钢-混组合梁经70年加载后,仅考虑混凝土徐变效应下产生的挠度是瞬时加载挠度的1.32倍,考虑混凝土收缩徐变效应产生的挠度是瞬时挠度的1.58倍.因此,混凝土长期荷载效应对两跨连续钢-混组合梁的挠度有较大影响,在工程设计和施工中应引起重视.
参考文献
[1]项贻强,郭树海.复杂应力条件下快速施工钢-混组合梁群钉推出试件参数分析[J].中国公路学报,2017,30(3):246—254. XIANG Y Q,GUO S H. Parameter analysis of push-out specimens with different group studs in accelerated bridge construction steelconcrete composite beams under complicated stress condition[J]. China Journal of Highway and Transport,2017,30(3):246—254.(In Chinese)
[2]王潇碧,宋瑞年,占玉林,等.钢-混凝土组合梁长期行为模拟及计算方法[J].工业建筑,2020,50(4):132—137. WANG X B,SONG R N,ZHAN Y L,et al. Simulation and calcula-tion method of long -term behavior of steel -concrete composite beams[J]. Industrial Construction,2020,50(4):132—137.(In Chinese)
[3]DEZI L,TARANTINO A M. Creep in composite continuous beams. I:theoretical treatment[J]. Journal of Structural Engineering,1993,119(7):2095—2111.
[4]DEZI L,TARANTINO A M. Creep in composite continuous beams. II:parametric study[J]. Journal of Structural Engineering,1993,119(7):2112—2133.
[5]CHENG H G. Analysis of stress and deflection about steel-concrete composite girders considering slippage and shrink & creep under bending[J]. The Open Civil Engineering Journal,2015,9(1):171—176.
[6]CAO G H,HAN C C,DAI Y,et al. Long-term experimental study on prestressed steel -concrete composite continuous box beams[J]. Journal of Bridge Engineering,2018,23(9):04018067.
[7]TONG T,YU Q,SU Q T. Coupled effects of concrete shrinkage,creep,and cracking on the performance of postconnected prestressed steel-concrete composite girders[J]. Journal of Bridge Engineering,2018,23(3):04017145.
[8]项贻强,何超超,邱政.体外預应力钢-混组合梁长期滑移计算[J].浙江大学学报(工学版),2017,51(4):739—744. XIANG Y Q,HE C C,QIU Z. Calculation of long-term slippage for externally prestressing steel-concrete composite beam[J]. Journal of Zhejiang University(Engineering Science),2017,51(4):739—744.(In Chinese)
[9]肖岩,彭罗文,KUNNATH S.组合梁考虑滑移效应的理论分析[J].湖南大学学报(自然科学版),2017,44(1):77—86. XIAO Y,PENG L W,KUNNATH S. Analysis of composite beams with interlayer slip[J]. Journal of Hunan University(Natural Sci-ences),2017,44(1):77—86.(In Chinese)
[10]冀伟,孙斌,邓露,等.多因素影响下钢-混连续组合梁的挠度计算分析[J].湖南大学学报(自然科学版),2019,46(5):30—38. JI W,SUN B,DENG L,et al. Calculation and analysis on deflection of steel-concrete continuous composite girder considering effect of multi-factors[J]. Journal of Hunan University(Natural Sciences),2019,46(5):30—38.(In Chinese)
[11]褚少辉,赵士永,张艳玲,等.钢-混凝土简支组合梁的非线性有限元分析[J].河北工业大学学报,2019,48(1):91—96. CHU S H,ZHAO S Y,ZHANG Y L,et al. Non-linear finite element analysis of steel-concrete simply supported composite beams[J]. Journal of Hebei University of Technology,2019,48(1):91—96.(In Chinese)
[12]NGUYEN Q H,HJIAJ M. Nonlinear time-dependent behavior of composite steel-concrete beams[J]. Journal of Structural Engineer-ing,2016,142(5):04015175.
[13]周凌宇,余志武,蒋丽忠.钢-混凝土组合梁界面滑移剪切变形的双重效应分析[J].工程力学,2005,22(2):104—109. ZHOU L Y,YU Z W,JIANG L Z. Analysis of composite beams of steel and concrete with slip and shear deformation[J]. Engineering Mechanics,2005,22(2):104-109.(In Chinese)
[14]黃侨,李文贤,汪炳.考虑界面滑移与剪切变形的钢-混凝土组合梁解析方法[J].南京航空航天大学学报,2018,50(1):131—137. HUANG Q,LI W X,WANG B. Analytical method of steel-concrete composite beam based on interface slip and shear deformation[J]. Journal of Nanjing University of Aeronautics & Astronautics,2018,50(1):131—137.(In Chinese)
[15]WANG S H,TONG G S,ZHANG L. Reduced stiffness of composite beams considering slip and shear deformation of steel[J]. Journal of Constructional Steel Research,2017,131:19—29.
[16]项海帆.高等桥梁结构理论[M]. 2版.北京:人民交通出版社,2013:316—332. XIANG H F. Advanced theory of bridge structure[M]. 2nd ed. Bei-jing:China Communications Press,2013:316—332.(In Chinese)
[17]樊健生,聂建国,王浩.考虑收缩、徐变及开裂影响的组合梁长期受力性能研究(Ⅰ):试验及计算[J].土木工程学报,2009,42(3):8—15. FAN J S,NIE J G,WANG H. Long -term behavior of composite beams with shrinkage,creep and cracking(I):experiment and cal-culation[J]. China Civil Engineering Journal,2009,42(3):8—15.(In Chinese)
[18]NGUYEN Q H,HJIAJ M,UY B. Time-dependent analysis of com-posite beams with continuous shear connection based on a spaceexact stiffness matrix[J]. Engineering Structures,2010,32(9):2902—2911.
