钢纤维混凝土的本构模型及力学性能分析
2021-02-09毕继红霍琳颖赵云王照耀
毕继红 霍琳颖 赵云 王照耀
摘要:为充分研究钢纤维混凝土的力学性能,基于混凝土的弥散开裂模型,并考虑纤维与混凝土之间的黏结作用,建立了新的钢纤维混凝土本构模型.在模型中分两种情况考虑纤维作用,混凝土开裂前,纤维与混凝土完全黏结,服从复合材料理论;混凝土开裂后,将分别考虑混凝土和钢纤维的贡献.通过黏结滑移模型,计算钢纤维在混凝土中脱黏和拔出过程中,纤维对开裂后混凝土的增强作用.采用Fortran编程,利用有限元软件ABAQUS中提供的子程序Umat,将提出的本构模型引入ABAQUS,并用于有限元模型去模拟钢纤维混凝土的拉伸和四点弯曲试验.通过数值模拟结果和试验数据的对比,充分验证了所提出的钢纤维混凝土本构模型的准确性.并对钢纤维混凝土的受拉强度、残余强度、受弯强度以及韧性等力学性能进行详细的分析.
关键词:钢纤维混凝土;弥散开裂模型;黏结滑移理论;复合理论;抗弯强度
中图分类号:TU528.572文献标志码:A
基金项目:国家自然科学基金资助项目(51227006),National Natural Science Foundation of China(51227006);天津市自然科学基金资助项目(18JCYBJC90800),Natural Science Foundation of Tianjin(18JCYBJC90800)
Constitutive Model and Mechanical Properties of Steel Fiber Reinforced Concrete
BI Jihong1,2,HUO Linying1,ZHAO Yun1,WANG Zhaoyao1
(1. School of Civil Engineering,Tianjin University,Tianjin 300350,China;2. Key Laboratory of Coast Civil Structure Safety(Tianjin University),Ministry of Education,Tianjin 300072,China)
Abstract:In order to study the mechanical properties of steel fiber reinforced concrete(SFRC),a new constitu-tive model of SFRC is established in this paper based on the smeared crack model of the plain concrete and consider-ing the bonding effect between fiber and concrete. In this model,the reinforcement of the steel fiber is considered in two cases. Before the cracking,the steel fiber and concrete matrix are fully bonded,which meets the two-phase com-posite law. When the concrete crack initiates and propagates,the contribution of the concrete and the steel fiber is considered separately. And the strengthening effect of fiber on the concrete cracked plane is considered through the bond-slip model during the process of fiber partially debonded and fully debonded from the concrete matrix. Through Fortran programming,the proposed constitutive model is introduced into ABAQUS software by using the subroutine Umat,and the finite element model is established to simulate the tensile tests and 4-points flexural tests of SFRC. Though the comparison of numerical simulation results and available experimental data,the accuracy of the constitu-tive model is verified. Meanwhile,the mechanical properties of SFRC including tensile strength,residual strength,flexural strength,and toughness are analyzed in detail.
Key words:steel fiber reinforced concrete(SFRC);smeared crack model;bond-slip model;two-phase compos-ite law;flexural strength
纖维混凝土在工程建设中越来越多的被使用,而钢纤维是实际工程应用中最常用的纤维类型[1-3].加入钢纤维可以在保持混凝土原有优势的基础上,对普通混凝土易开裂,抗拉、抗弯强度低以及韧性差等不足有了显著改善,使混凝土在工程中有更广泛的应用前景[4-5].
国内外学者关于钢纤维混凝土(SFRC)的力学性能做了大量的相关试验,梁兴文等人[1-2]做了大量的纤维混凝土的抗拉试验和纤维混凝土梁的四点弯曲试验,并拟合了钢纤维混凝土的单向受拉本构模型和梁的抗弯强度的计算公式;邓宗才[4]进行161个三点弯曲梁的断裂试验,测定了不同纤维掺量下试件的荷载-挠度曲线.通过大量的力学试验可知,在混凝土开裂后,钢纤维在开裂面上纤维桥接现象,对混凝土的抗拉强度、抗折强度、韧性均有显著提高作用.
钢纤维混凝土力学性能的研究远不能满足实际工程的需要,目前主要依靠试验和对试验结果的拟合,缺乏理论支撑.近年来,钢纤维混凝土力学性能的理论研究引发了国内外学者的广泛关注.通常基于经典的混凝土本构模型,包括:混凝土弥散本构模型、混凝土损伤本构模型以及混凝土断裂模型,考虑钢纤维对混凝土基体的增强作用,从而建立钢纤维混凝土的本构模型.池寅等人基于有限元软件ABAQUS中混凝土的损伤本构模型,考虑纤维对混凝土受拉屈服函数和损伤因子的确定的影响,建立了考虑纤维作用的混凝土损伤本构模型;Olesen[7]基于混凝土断裂力学中虚拟裂纹模型,在裂缝扩展中将纤维视为铰链,分层考虑纤维和混凝土对承载力的贡献;薛云亮等人[8]通过大量的纤维混凝土试验,基于两参数Weibull分布函数引入纤维对损伤本构中损伤阈值影响,建立了可考虑损伤阈值影响的钢纤维混凝土损伤本构模型.
然而,现有的纤维混凝土本构模型,通常认为在混凝土开裂后,纤维在裂缝扩展过程中增强作用保持不变.事实上,随着混凝土裂缝的扩展,开裂面上的钢纤维与混凝土基体间拔出过程分为部分脱黏和完全脱黏两个阶段,这2个阶段具有不同的纤维增强应力.
在混凝土开裂后,充分考虑钢纤维在混凝土中由充分黏结、逐渐脱黏直到完全脱黏,然后拔出的全过程,本文提出了一个三维钢纤维随机分布的混凝土弥散开裂本构模型.并利用Fortran编程,通过有限元软件ABAQUS的子程序接口Umat,将本文提出的钢纤维混凝土本构模型引入ABAQUS的材料库中,并利用该本构模型在ABAQUS中建立混凝土受拉试件和四点弯曲梁的有限元模型.通过比较试验数据和数值模拟结果,验证了所提出的材料本构模型的准确性.
1混凝土及纤维的本构模型
在钢纤维混凝土中,钢纤维作为掺加物加入混凝土基质中,其中对混凝土基质采用弥散开裂本构模型,对掺入的钢纤维采用理想弹塑性本构模型.
1.1弥散开裂本构模型



3纤维在裂缝处的增强作用
在混凝土开裂前,钢纤维没有桥接作用,因此钢纤维不影响混凝土的开裂应力[17 -18].在混凝土开裂后,钢纤维在混凝土开裂面上,形成纤维桥接,主要承擔开裂后的荷载.钢纤维可以有效阻止混凝土裂缝的扩展[17].
3.1混凝土的开裂准则及裂缝宽度
由于钢纤维不影响混凝土的开裂强度,因此钢纤维混凝土的开裂准则,仍采用普通混凝土的判别方式.本文所采用的是ABAQUS中混凝土弥散开裂本构模型的开裂准则,将混凝土的受拉屈服面作为“裂缝检测面”,当混凝土应力达到裂缝检测面时,裂缝出现[17].混凝土的裂缝方向被定义为最大主塑性应变增量与混凝土受拉屈服面所共轭的方向.




4有限元模型的试验验证
基于Fortran编程和有限元软件ABAQUS中的自定义材料本构模型的子程序接口Umat,将钢纤维混凝土的本构模型引入到ABAQUS,并用于有限元数值模拟[28].图3给出了子程序Umat编程计算中的一个完整的循环过程.

利用Li等人[29]的钢纤维混凝土受拉试验和高丹盈等人[30]的钢纤维混凝土的四点弯曲试验,分别在ABAQUS中建立相应的有限元模型,验证本文提出的钢纤维混凝土弥撒开裂本构模型的正确性.
4.1建立受拉试验的有限元模型
依据Li等人[29]进行的普通混凝土及钢纤维混凝土单向受拉试验,本文利用有限元软件ABAQUS进行了数值模拟.
首先,在ABAQUS中建立几何尺寸为100 mm×100 mm×1 000 mm的几何模型,通过约束模型右侧单元的自由度建立固定的边界条件,并从模型左侧进行位移加载.受拉模型的网格尺寸、边界条件及加载均如图4所示.

选择在ABAQUS中建立针对钢纤维混凝土的弥散开裂本构模型;为有限元模型选择三维八节点六面体实体单元(C3D8),并采用ABAQUS中用户自定义的材料本构模型,选用线性完全积分单元.试验中采用的钢纤维均为圆形横截面且具有高长径比,混凝土材料及钢纤维的力学性能已在表1和表2中具体给出.本构模型中其他参数的确定参考王金昌等人[13]:单轴与双轴的抗压强度之比为1.18,单轴抗拉与单轴抗压应力之比为0.1,双轴与单轴压应变之比为1.25,拉伸开裂应力与压缩应力之比为0.2.

4.2受拉试验的模型验证及数值分析
在图5中,通过比较钢纤维混凝土和普通混凝土在受拉状态下的应力-应变曲线,可以发现数值模拟结果与试验数据均吻合良好,抗拉强度及所对应的应变值的误差均较小.能够很好地说明钢纤维对混凝土裂缝发展的控制,充分证明了本文提出的本构模型在单向受拉情况下的准确性.
通过分别加入体积分数2%、3%的钢纤维,混凝土的抗拉强度从4 MPa提高到4.75 MPa和5.5MPa,提高了19%和37%;残余应力强度从0.65 MPa提高到3.68MPa和5.2MPa,分别提高了5.7倍和8倍.使混凝土在达到峰值强度后,仍保持良好的性能,纤维对混凝土的抗拉强度和残余应力均有显著的增强.
这是由于混凝土开裂后,在开裂面上的钢纤维,通过桥接作用主要承担开裂面上的应力,使混凝土在开裂后继续受拉.且随着裂缝的扩展,钢纤维与混凝土之间逐步脱黏、拔出,并在该过程中纤维持续承受拉应力.因此,相比于普通混凝土,抗拉强度及残余强度均有了显著的提高.

与普通混凝土相比,钢纤维混凝土在达到开裂强度后,应力持续增长,出现硬化,且在达到抗拉强度后应力缓慢下降,仍有较强的残余应力,说明本文所建立的本构模型充分反映了钢纤维对控制裂缝扩展的作用.
将现有模型对钢纤维掺量2%的SFRC的受拉模拟结果,与本文所提出的本构模型以及文献中的模型的数值模拟结果进行了对比,如表3所示.

由表3可知,本文提出的本构模型对峰值应力和残余应力的模拟比较准确,相对误差平均值小于5%.本研究的数值模拟结果的误差处于相对较低的水平.
4.3建立弯曲试验的有限元模型
基于高丹盈等人[30]进行的SFRC梁的四点弯曲试验,在有限元软件ABAQUS中建立几何尺寸为100 mm×100 mm×400 mm的钢纤维混凝土梁,其中,梁跨度为300 mm;试样宽度和深度均为100 mm.试验采用长度50 mm直径0.9 mm的钢纤维,其中混凝土基质的力学性能如表4所示.

为了充分模拟弯曲试验,避免在计算过程中出现应力集中现象,在有限元模型中为SFRC梁建立加载板和支座.通过加载板对混凝土施加竖向荷载,在支座一侧设置限制水平位移的转动边条,另一侧设置水平方向自由的转动边条.
在试验加载过程中,SFRC梁不仅在支座处存在转动,同时存在与支座的滑移现象.因此,在模型中,对于SFRC梁与支座和加载板之间分别建立接触,在接触面法向方向采用“硬接触”,切向方向采用摩擦理论,摩擦系数取值为0.6[27].
同样采用线性完全积分的三维八节点六面体实体单元(C3D8)来建立SFRC梁模型.并选择在ABAQUS中建立的针对于SFRC的本构模型,该模型边界条件、加载情况和网格类型如图6所示.

4.4弯曲试验的模型验证及数值分析
将有限元模型模拟的SFRC梁的四点加载试验的荷载位移曲线与高丹盈等人的试验数据进行比较,如图7所示.荷载位移曲线中斜率的第一个转折点为SFRC梁的开裂点,对应的荷载为SFRC初裂荷载.有限元模拟结果与试验数据吻合良好,具体对比SFRC的初裂荷载、荷载峰值与试验结果的误差值均在5%左右.

由表5可知,在混凝土中摻入钢纤维对混凝土梁初裂荷载影响不大,普通混凝土和钢纤维混凝土梁均在荷载达到约20 kN时,出现开裂.这与建立SFRC的本构模型时做出的假设相吻合.普通混凝土在开裂后直接脆性破坏;而对于钢纤维混凝土,在混凝土开裂后,开裂面上的钢纤维形成纤维桥接作用,继续承担荷载,并在混凝土梁达到峰值荷载之后,仍保持较高的荷载强度.

在图8中分别给出了钢纤维混凝土梁和普通混凝土梁的强度-位移曲线.钢纤维的掺入使混凝土的抗弯强度由6 MPa提高到9.4 MPa,增强幅度超过50%.

如表6所示,钢纤维对混凝土增强的作用不仅是SFRC的承载和变形,同时对混凝土的韧性有显著的增强作用.

钢纤维混凝土梁的纯弯部分在梁高方向出现了显著的变形,如图10所示.整个纯弯部分向下挠曲变形,整个混凝土梁通过支座发生扭转,支座两侧部分出现少量的抬高.

图11给出了钢纤维混凝土梁在不同荷载阶段梁长方向的应力云图.在整个加载过程中SFRC梁中的压应力始终小于SFRC的抗压强度,因此,SFRC梁中受压作用部分均用深灰色表示.

由初裂时刻仅在纯弯段底部最下层应力达到混凝土抗拉强度,其他部分的拉应力值较小,同时梁上侧混凝土处于受压状态;在荷载达到峰值时,梁大部分处于受拉状态,中性轴明显上移,最大应力的位置从最下层上移,SFRC梁底部的钢纤维混凝土进入了塑性软化阶段;在SFRC梁最终破坏时,最大应力的位置继续上移,裂缝进一步扩展.
随着荷载的施加,钢纤维混凝土梁塑性应变量随之变大,塑性变形范围也相应增大,如图12所示.在SFRC梁的初裂时刻,仅在纯弯段底部最下层出现塑性变形;当达到荷载峰值后,SFRC梁的纯弯段中大部分都已进入塑性阶段.

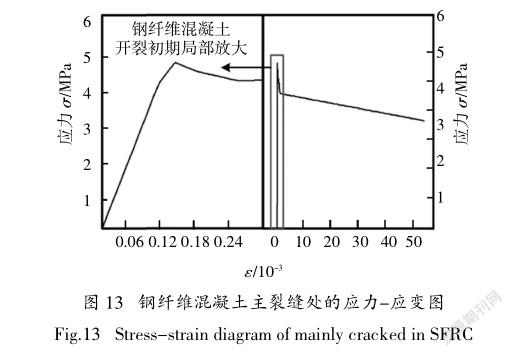
如图13所示,在纯弯段部分混凝土梁开裂后,在纤维桥接作用下,纤维混凝土应力增强,达到应力峰值后,进入软化段直至钢纤维混凝土梁破坏.
5结论
本文基于普通混凝土的弥散开裂模型,并考虑在混凝土开裂后,钢纤维与混凝土界面脱黏过程以及钢纤维在混凝土拔出过程,提出了一种钢纤维混凝土的弥散开裂本构模型.
通过Fortran编程和ABAQUS子程序接口U-mat,将本文提出的钢纤维混凝土本构模型引入到ABAQUS的材料库中.基于单向受拉试验和四点弯曲试验,分别建立有限元模型,并通过对比试验数据和有限元的数值模拟结果,充分验证了本文所提出的钢纤维混凝土本构模型的准确性.
基于单向受拉试验的数值模拟,加入钢纤维对混凝土抗拉强度和残余强度均有显著的增强作用,使混凝土在达到峰值强度后,仍具有良好的力学性能.钢纤维混凝土在达到开裂强度后,由于开裂面上钢纤维的桥接作用,钢纤维混凝土开裂后应力持续增长出现硬化,在达到抗拉强度后缓慢下降.
在四点弯曲试验的模拟中,纤维加入大幅度提高了混凝土的弯曲强度,有效地改善了混凝土韧性的不足.同时,通过对比试验数据和数值模拟的开裂荷载,验证了在本构模型建立时,忽略钢纤维对混凝土初裂强度影响的合理性.
参考文献
[1]胡翱翔,梁兴文,于婧,等.超高性能混凝土轴心受拉力学性能试验研究[J].湖南大学学报(自然科学版),2018,45(9):30—37. HU A X,LIANG X W,YU J,et al.Experimental study of uniaxial tensile characteristics of ultra-high performance concrete[J].Jour-nal of Hunan University(Natural Sciences),2018,45(9):30—37.(In Chinese)
[2]梁兴文,胡翱翔,于婧,等.钢纤维对超高性能混凝土抗弯力学性能的影响[J].复合材料学报,2018,35(3):722—731. LIANG X W,HU A X,YU J,et al.Effect of steel fibers on the flexu-ral response of ultra-high performance concrete[J].Acta Materiae Compositae Sinica,2018,35(3):722—731.(In Chinese)
[3]方志,向宇,匡镇,等.钢纤维含量对活性粉末混凝土抗疲劳性能的影响[J].湖南大学学报(自然科学版),2011,38(6):6—12. FANG Z,XIANG Y,KUANG Z,et al.Fatigue properties of reactive powder concrete with different steel fiber ratios[J].Journal of Hu-nan University(Natural Sciences),2011,38(6):6—12.(In Chi-nese)
[4]鄧宗才.混杂纤维增强超高性能混凝土弯曲韧性与评价方法[J].复合材料学报,2016,33(6):1274—1280. DENG Z C.Flexural toughness and characterization method of hybrid fibers reinforced ultra-high performance concrete[J].Acta Materiae Compositae Sinica,2016,33(6):1274—1280.(In Chinese)
[5]MIHAI I C,JEFFERSON A D,LYONS P.A plastic-damage consti-tutive model for the finite element analysis of fibre reinforced con-crete[J].Engineering Fracture Mechanics,2016,159:35—62.
[6]池寅,黄乐,余敏.基于ABAQUS的钢-聚丙烯混杂纤维混凝土损伤塑性本构模型取值方法研究[J].工程力学,2017,34(12):131—142. CHI Y,HUANG L,YU M.Calibration method of damage plasticity model for steel -polypropylene hybrid fiber reinforced concrete based on Abaqus[J].Engineering Mechanics,2017,34(12):131—142.(In Chinese)
[7]OLESEN J F.Fictitious crack propagation in fiber-reinforced con-crete beams[J].Journal of Engineering Mechanics,2001,127(3):272—280.
[8]薛云亮,李庶林,林峰,等.考虑损伤阈值影响的钢纤维混凝土损伤本构模型研究[J].岩土力学,2009,30(7):1987—1992. XUE Y L,LI S L,LIN F,et al.Study of damage constitutive model of SFRC considering effect of damage threshold[J].Rock and Soil Me-chanics,2009,30(7):1987—1992.(In Chinese)
[9]FEENSTRA P H,DE BORST R.A composite plasticity model for concrete[J].International Journal of Solids and Structures,1996,33(5):707—730.
[10]殷有泉.岩石类材料塑性力学[M].北京:北京大学出版社,2014:35—46. YIN Y Q. Rock plastic mechanics[M]. Beijing:Beijing University Press,2014:35—46.(In Chinese)
[11]KUPFER H B,GERSTLE K H.Behavior of concrete under biaxial stresses[J].Journal of the Engineering Mechanics Division,1973,99(4):853—866.
[12]吳建营,李杰.混凝土的连续损伤模型和弥散裂缝模型[J].同济大学学报(自然科学版),2004,32(11):1428—1432. WU J Y,LI J.Continuum damage mechanics model and smearedcrack model for concrete[J].Journal of Tongji University,2004,32(11):1428—1432.(In Chinese)
[13]王金昌,陈页开. ABAQUS在土木工程中的应用[M].杭州:浙江大学出版社,2006:225—226. WANG J C,CHEN Y K. Application of ABAQUS in civil engineer-ing[M]. Hangzhou:Zhejiang University Press,2006:225—226.(In Chinese)
[14]钢纤维混凝土:JG/T 472—2015[S].北京:中国标准出版社,2015. Steel fiber reinforced concrete:JG/T 472—2015[S].Beijing:Stan-dards Press of China,2015.(In Chinese)
[15]MARARA K,ERENB?,YITMENA?. Compression specific tough-ness of normal strength steel fiber reinforced concrete(NSSFRC)and high strength steel fiber reinforced concrete(HSSFRC)[J]. Materials Research,2011,14(2):239—247.
[16]GARG S K,SVALBONAS V,GURTMAN G A. Analysis of struc-tural composite materials[M]. New York:Marcel Dekker Inc,1973:18—23.
[17]HILLERBORG A,MOD?ER M,PETERSSON P E.Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements[J].Cement and Concrete Research,1976,6(6):773—781.
[18]EDALAT-BEHBAHANI A,BARROS J A O,VENTURA-GOU-VEIA A.Three dimensional plastic-damage multidirectional fixed smeared crack approach for modelling concrete structures[J].Inter-national Journal of Solids and Structures,2017,115/116:104—125.
[19]MORTAZAVIAN S,FATEMI A.Effects of fiber orientation and anisotropy on tensile strength and elastic modulus of short fiber re-inforced polymer composites[J].Composites Part B:Engineering,2015,72:116—129.
[20]FU S Y,LAUKE B.Effects of fiber length and fiber orientation dis-tributions on the tensile strength of short-fiber-reinforced polymers[J].Composites Science and Technology,1996,56(10):1179—1190.
[21]SEBAIBI N,BENZERZOUR M,ABRIAK N E.Influence of the dis-tribution and orientation of fibres in a reinforced concrete with waste fibres and powders[J].Construction and Building Materials,2014,65:254—263.
[22]HSUEH C H.Interfacial debonding and fiber pull-out stresses of fiber-reinforced composites Part VI.Interpretation of fiber pull-out curves[J].Materials Science and Engineering:A,1991,149(1):11—18.
[23]赵国藩,彭少民,黄承逵.钢纤维混凝土结构[M].北京:中国建筑工业出版社,1999:48—50. ZHAO G F,PENG S M,HUANG C K. Steel fiber reinforced con-crete structure[M]. Beijing:China Architecture & Building Press,1999:48—50.(In Chinese)
[24]DAI J G,UEDA T.Local bond stress slip relations for FRP sheetsconcrete interfaces[C]//Fibre-reinforced Polymer Reinforcement forConcrete Structures.Singapore:World Scientific Publishing Compa-ny,2003:143—152.
[25]LIU H Y,ZHOU L M,MAI Y W.On fibre pull-out with a rough in-terface[J].Philosophical Magazine A,1994,70(2):359—372.
[26]TAI Y S,EL -TAWIL S,CHUNG T H.Performance of deformed steel fibers embedded in ultra-high performance concrete subjected to various pullout rates[J].Cement and Concrete Research,2016,89:1—13.
[27]蘇庆田,杜霄,李晨翔,等.钢与混凝土界面的基本物理参数测试[J].同济大学学报(自然科学版),2016,44(4):499—506. SU Q T,DU X,LI C X,et al.Tests of basic physical parameters of steelconcrete interface[J].Journal of Tongji University(Natural Science),2016,44(4):499—506.(In Chinese)
[28]ZHANG S L,WANG Q G,ZHOU W X.Implementation of the Tresca yield criterion in finite element analysis of burst capacity of pipelines[J].International Journal of Pressure Vessels and Piping,2019,172:180—187.
[29]LI Z J,LI F,CHANG T Y P,et al. Uniaxial tensile behavior of con-crete reinforced with randomly distributed short fibers[J]. ACI Ma-terials Journal,1998,95(5):564—574.
[30]高丹盈,赵亮平,冯虎,等.钢纤维混凝土弯曲韧性及其评价方法[J].建筑材料学报,2014,17(5):783—789. GAO D Y,ZHAO L P,FENG H,et al.Flexural toughness and it’s evaluation method of steel fiber reinforced concrete[J].Journal of Building Materials,2014,17(5):783—789.(In Chinese)
[31]OTHMAN H,MARZOUK H.Applicability of damage plasticity constitutive model for ultra-high performance fibre-reinforced con-crete under impact loads[J].International Journal of Impact Engi-neering,2018,114:20—31.
[32]LE L A,NGUYEN G D,BUI H H,et al.Incorporation of microcracking and fibre bridging mechanisms in constitutive modelling of fibre reinforced concrete[J].Journal of the Mechanics and Physics of Solids,2019,133:103732.
[33]Standard test method for flexural performance of fiber reinforced concrete(using beam with thirdpoint loading): ASTM C1609[S]. Philadelphia: ASTM Internation, 2006:1—8.
[34]Standard test method for flexural toughness and first-crack strength of fiber reinforced concrete:ASTM C 1018[S]. West Conshohock-en:ASTM Internation,1997:544.
