随机地震激励作用下自复位结构的平稳响应

胡慧瑛，陈林聪,2

(1.华侨大学 土木工程学院，福建 厦门 361021；2.福建省智慧基础设施与监测重点实验室，福建 厦门 361021)

地震对人类社会的危害不言而喻。传统结构虽然能有效保障人员的生命财产安全，但震后往往存在结构倒塌、残余变形过大等问题，使得结构震后修复成本过高。近来，为了减少结构震后修复产生的经济损失，工程界致力于研究可恢复功能结构[1-5]。可恢复功能结构是指在震中不发生破坏或是仅发生可以迅速修复破坏的结构，因此能显著减小震后修复所需的时间成本和经济成本。自复位结构作为可恢复功能结构中的一种，逐渐成为国内外学者的研究热点。已有研究表明，自复位结构不仅具有与传统结构大致相当的耗能能力，还能有效消除结构的残余变形，大大减小了结构震后修复负担。

目前有关自复位结构的研究成果丰硕。在响应预测方面，常用方法有时程分析法[6-7]以及平均法[8-9]，但这些研究多是在确定性激励下进行，鲜有涉及随机激励环境。众所周知，地震地面运动具有明显的随机性。在随机地震动作用下自复位系统的响应也是一个随机过程。最近，胡晓斌等[10]利用等效线性化法建立了单自由度自复位系统随机地震响应的求解流程。然而，等效线性化仅能获得系统的高斯响应，低估了响应位移与速度的均方值，以致结果偏于不安全。另外，上述研究中采用了高斯白噪声激励模型，该激励能量在频域内是均匀分布的，有悖于实际情况[11]。因此，非常有必要发展一种更有效的方法来确定自复位系统的随机地震响应，同时亦需引入一种能更好模拟地震作用的数学模型。

随机平均法是将随机平均原理与FPK方程法相结合的一类方法。该法是分析非线性随机系统最有效的方法之一。近年来，随机平均法被广泛的运用于非线性系统与随机参激系统的随机响应预测、可靠性估计及随机稳定性判别。Roberts和Spanos[12]以及朱位秋[13]等均对随机平均法的应用发展做出了严谨的综述。随机平均法最突出的优点是可以降维，从而降低求解FPK方程的难度，特别是对于拟不可积哈密顿系统[14]，平均后的系统是一维的。与等效线性化方法相比，随机平均方法还具有克服概率密度不准确、保持原系统主要非线性特征等显著优点。

国内外学者相继提出多种过滤白噪声模型来模拟地震作用，目前常用分析谱模型有杜修力谱[15]、欧进萍谱[16]、金井清谱[17]等。金井清过滤白噪声模型是在白噪声模型的基础上，进一步考虑地表土层特性对地震动频谱特征的影响，物理意义明确且能较好地模拟地震地面运动特性，在实际中得到广泛应用。本文考虑到地震动的随机性，应用随机平均法研究了金井清过滤白噪声激励下单自由度自复位系统的平稳响应。首先利用广义谐波平衡技术，将旗帜形的恢复力解耦为幅值依赖的等效拟线性弹性力和拟线性阻尼力，得到原系统的等效非线性系统；然后，应用基于广义谐和函数的随机平均法将等效非线性系统简化为关于系统幅值的平均伊藤方程，建立并求解与之相应FPK方程得到系统幅值的稳态概率密度函数；研究系统关键参数对系统响应的影响，并通过蒙特卡罗模拟对理论解析结果进行验证。

1 随机地震荷载作用下单自由度自复位系统

随机地震荷载作用下单自由度自复位系统的运动微分方程可以表示为，

(1)

(2)

式中:ωg、ξg分别为地震波传播过程中所经历土层的特征频率和阻尼比；S0为位于震源处的基岩传给上层的白噪声功率谱密度；该模型的自复位体系的恢复力常用FS(Flag-shaped)模型描述，如图1(a)所示，由图1可得，自复位体系恢复力可以分解为弹性力(图1(b))和滞变力(图1(c)),即

(a)旗帜形恢复力模型

(3)

式中：Z是滞变位移，α为能量耗散系数。

如图2所示，滞变位移Z可以分段表示为，

图2 自复位体系滞变位移

(4)

(5)

式中：β、Xy、A分别表示能量耗散系数、屈服位移和系统位移幅值。

将式(4)、(5)代入式(3)中，恢复力的表达式可整理为，

(6)

(7)

2 等效非线性系统

由图1可知，式(6)与(7)中表示的恢复力同时影响系统的阻尼和刚度。根据广义谐波平衡技术，恢复力可解耦为幅值依赖的等效拟线性弹性力和拟线性阻尼力，

(8)

式中：

(9)

(10)

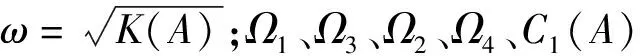
将式(8)代入式(1)，可得系统(1)的等效非线性系统，

(11)

系统(11)的总能量为，

(12)

式中：

(13)

3 随机平均

假设系统(11)解的形式为，

Y(t)=A(t)cosΘ(t)

(14)

式中：

Θ(t)=Φ(t)+Γ(t)

(15)

变量A(t)、Θ(t)与Г(t)均为随机过程。

(16)

(17)

式中：

(18)

当阻尼和激励较弱的时候，根据Stratonovich-Khasminskii极限定理[17],A,Г弱收敛于二维扩散Markov过程。需指出的是，关于A(t)的平均伊藤随机微分方程中不含Г(t)。关于A(t)的平均伊藤随机微分方程为，

(19)

式中：B(t)为单位维纳过程；平均漂移和扩散系数分别为，

(20)

式中R(τ)表示系统激励的自相关函数；〈·〉Θ表示对Θ作平均，即

(21)

为了进一步获得漂移与扩散系数的表达式，现将Gik展开为Fourier级数

Gik=Gik0(A)+

(22)

将式(22)代入式(20)，完成对τ的积分和对Θ的平均后，得

(23)

支配转移概率密度p(a|a0;t)满足的FPK方程为，

(24)

初始条件为，

p=δ(a-a0)

(25)

式中:a为系统幅值，a0为系统初始幅值。

当∂p/∂t=0时，方程(22)有如下的平稳精确解，

(26)

式中,C0为归一化常数。

4 参数分析

本节考察能量耗散系数β、屈服位移Xy和激励强度D1取值的变化对系统稳态概率密度函数的影响。选取系统参数为：c=0.05、α=0.2、ωg=10、ξg=0.9、D1=0.01。其中实线表示由方程式(26)得到的数值解结果，符号(△,□,◇)表示对原方程(1)直接进行蒙特卡罗的结果。观察每幅图像都可以看出理论解和蒙特卡罗解在误差允许范围内吻合，表明文中提出的求解方法有效。

图3～5给出了当能量耗散系数β=0.5，β=1.0与β=2.0时，屈服位移Xy取值的变化对系统响应的影响。从这三个图中均可看出，当Xy<1.0时，p(a)随着Xy的减小向左偏移并在较小a处达到峰值。这说明屈服位移的降低可有效减小系统响应。该现象可用图8来解释，当能量耗散系数一定时，随着Xy的减小，滞回曲线的面积增大，即系统的耗能性能提高。而当Xy>1.0时，Xy的减小并不能有效的减小系统响应。此外，由于旗帜形恢复力是分段函数，当Xy=1.0时，p(a)在分段点a=Xy处存在不光滑现象，该现象β=2.0时最为明显,见图5。

图3 β=0.5时系统关于幅值的稳态概率密度函数

图4 β=1.0时系统关于幅值的稳态概率密度函数

图5 β=2.0时系统关于幅值的稳态概率密度函数

图6中，研究了屈服位移Xy=0.5时，能量耗散系数β对系统稳态响应的影响。由图6可看出，β的变化对系统的稳态响应的大小影响不大，但随着β的增加，p(a)逐渐接近于正态分布，与此同时，p(a)在分段点处不光滑现象越来越明显。

图6 Xy=0.5时系统关于幅值的稳态概率密度函数

图7中，研究了屈服位移Xy=1.0且能量耗散系数β=1.0时，激励强度D1对系统稳态响应的影响。从图7可看出，理论解和蒙特卡罗解吻合的非常好。

图7 Xy=1.0,β=1.0时系统关于幅值的稳态概率密度函数

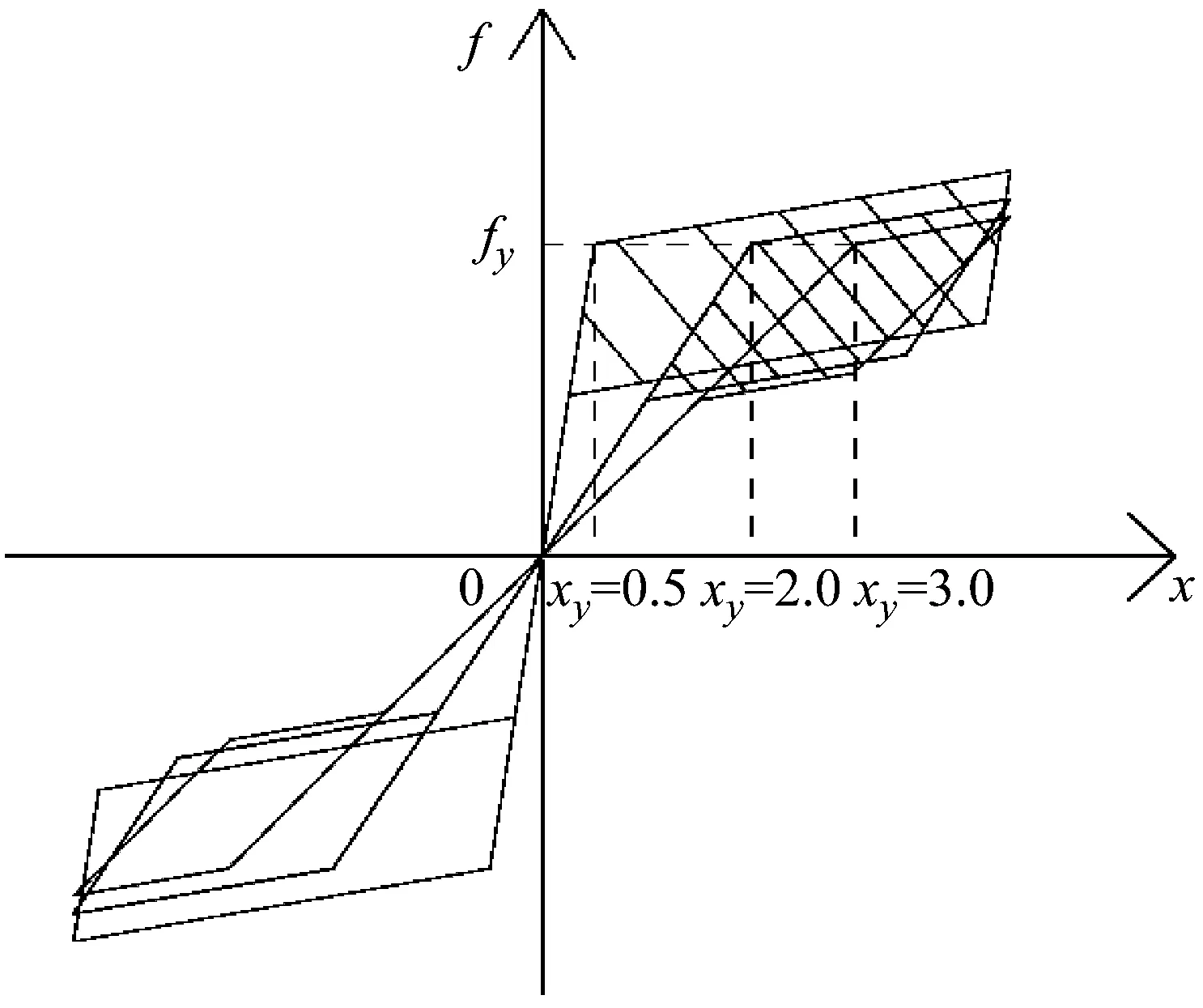
图8 β=0.5时旗帜形滞回曲线所围面积

5 结 论

本文研究了基于金井清谱随机地震激励下单自由度自复位体系的平稳响应。运用广义谐波平衡技术，得到原系统的等效非线性方程。通过van der Pol变换和随机平均法，得到关于系统幅值的平均伊藤方程。建立并求解相应的FPK方程，获得关于幅值的稳态概率密度函数，研究了能量耗散系数和屈服位移对系统稳态响应的影响。研究结论如下：

(1)当屈服位移小于1.0时，系统的稳态响应随着屈服位移的减小而降低；

(2)由于系统恢复力是分段函数，系统的稳态响应在分段点处存在不光滑现象，该现象在屈服位移为1.0且能量耗散系数为2.0时尤为明显；

(3)通过与蒙特卡罗模拟结果的对比发现理论解析解具有很好的精度。

附录A

系统(1)解的形式可以假设为以下广义谐波方程

X(t)=A(t)cosΘ′(t)

(A1)

对于A≤Xy,

(A2)

(A3)

对于A>Xy,

(A4)

(A5)

其中