伴流声场计算的有限元方法及其应用

范一良，季振林

(哈尔滨工程大学 动力与能源工程学院，哈尔滨 150001)

声波是由于介质的弹性效应引起的，相对于介质的质点在运动[1]。在消声器和管路系统中都存在气体的流动，气体的流动直接影响声波的传播，进而影响消声器的声学特性。对于等截面或渐变截面管道，假定管道内流体在垂直于轴线的横截面上以均匀速度流动，此时管道内的声传播可用解析方法求解[1-2]。但是多数消声器内部的流场是非均匀的，需要使用三维数值方法计算消声器内的流场并考虑流场对声场影响。由于问题的复杂性，通常假设传输声波的是无旋、无粘的运动介质，于是速度可以由一个标量函数的梯度来表示，这个标量函数被称为速度势。速度势可以进一步分解为不随时间发生变化的平均量和小扰动的声学量，结合流体的连续性方程、动量方程和状态方程得到伴流下的声波波动方程。

Danda等[3-4]在研究涡轮发动机风扇通道的声辐射时给出了势流中的波动方程，讨论了与之相关的声学边界条件，并在边界上采用近似方法用FEM编程计算出声场的分布，但是省略了详细的推导过程，后续相关研究[2]也是直接引用其结论。Myers[5]建立了掠过流下无粘流体中边界面上法向声质点振速与声质点法向位移、法向位移的梯度、平均流和圆频率之间的关系，法向位移又与声压通过声阻抗建立起联系，但表达式比较复杂，很难在FEM中编程实现。Eversman[6]在Myers的基础上研究声阻抗边界时，受到Moehring[7]的启发，得到了更加简化、准确、容易编程实现的表达式，随后该表达式被Eversman应用在可压缩势流的逆流定理与声学互易性[8]和管道内可压缩势流声学互易的数值实验[9]研究中，但Eversman只探讨了阻抗边界条件，对于声激励边界、穿孔阻抗边界和无反射边界则没有涉及。徐贝贝等将有限元法应用于计算穿孔管消声器的传递损失[10]，分析了穿孔率对消声器声学性能的影响，但仅限于无流情况。

Eversman省略了推导势流中的声波方程的过程，并且声边界条件的探讨也仅限于阻抗边界。本文补充势流中声波方程推导过程中的相关细节，运用伽辽金加权余量法建立相应的有限元弱形式，讨论和分析势流状态下管道声学计算的各种声边界条件，通过装配和组装得到弱形式的矩阵表达式，并给出有限元编程计算的相关细节。为验证理论和计算程序的正确性，使用自行编写的有限元程序计算H-Q管的传递损失，并与一维理论计算结果进行比较，之后将有限元法应用于分析流速和结构变化对H-Q管消声性能的影响。

1 伴流声学方程

假设消声器内部是无旋、无粘、定常的气体流动，对于任意空间位置固定的无穷小微团，微分形式的质量守恒方程为：

(1)

由于无粘，微团表面力只有压力，忽略体积力，则动量方程可表示为：

(2)

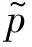
声音传播过程是等熵过程，对于等熵流体，状态方程可表示为：

(3)

式中，γ为比热比。

声速可以表示为：

(4)

(5)

把式(5)代入到式(2)中，得：

(6)

因为声波传递是等熵过程，所以密度只是压力的函数，式(6)可以写成：

(7)

式(7)只与时间有关，与空间无关，所以有：

(8)

式(8)为正压流的伯努利方程，F(t)为力势。对状态方程式(3)求导，并代入到式(8)的第三项中，可得：

(9)

把式(9)代入到式(8)得到：

(10)

用c和v分别表示远离反射体和吸声体等均匀无扰动流体中的常速声速和流体速度。在未被声扰动处，速度势函数不随时间发生变化，所以有：

(11)

将式(11)改写成：

(12)

声学理论是研究流场变量的小扰动行为。流体变量被分解为不随时间变化的平均量(用下标0表示)和小扰动的声学量(用下标a表示)。因此速度势、速度、密度和压强可以表示为：

(13a)

(13b)

(13c)

(13d)

式中:v0=φ0,va=φa。

将式(13(a))和(13(b))代入式(12)中，忽略高阶声学量，得：

(14)

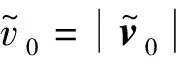
由式(14)可知，没有声扰动时，流动流体质中的声速为：

(15)

(16)

把式(16)代入式(15)中，可建立起静止流体和运动流体中的声速关系：

(17)

把式(15)代入到式(14)中，可得：

(18)

将式(13(c))代入到式(4)中，并将式(4)在ρ0处进行泰勒展开，保留一阶项，得：

(19)

综合式(18)和(19)可得声密度与声速度势之间的关系：

(20)

把式(13(c))和(13(d))代入式(3)中，并将式(3)在ρ0处进行泰勒展开，仅保留一阶项，得到：

(21)

把式(20)代入到式(21)中，得到声压与声速度势之间的关系：

(22)

把式(13(a))和(13(d))代入质量守恒方程中，即式(1)中，去掉守恒项和高阶项，得：

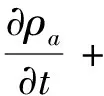
(23)

把式(20)代入到式(23)中，可得：

(24)

对于简谐声场，则有：

φa(x,y,z,t)=φ(x,y,z)ejωt

(25)

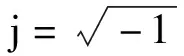
把式(25)代入到式(24)中，可得：

(26)

式(26)即为势流中的声波方程，当平均流速为零时，则简化为亥姆霍兹方程。

2 声学有限元方程

对式(26)应用伽辽金加权余量法，并对第一项使用格林第一公式，得：

(27)

式中:N为权函数，n为面单元的单位外法向量，上式即为弱形式的变分公式。

2.1 声学边界条件

消声器常用的边界条件如图1所示，包括入口处的激励面Si，声导纳面SR，穿孔面Sp1和Sp2，刚性壁面Sw，以及出口端So，将消声器分为两个域，分别用Ⅰ和Ⅱ标识。流场的入口面在声学上被当成刚性壁面来处理，这样会使声音只向下游传播，不向上游传播。边界将分为背景流与边界面平行和垂直两种情况讨论，当边界面法向方向与平均流速相切时，则有：

图1 消声器边界条件

φ0·n=0

(28)

把式(28)代入式(27)的等式右端中，则有：

(29)

式中，un为法向声质点振速。

Myers[5]给出了掠过流下无粘流体中简谐声激励下边界面上法向声质点振速un与法向位移ζn，平均流v0以及壁面单位法向量之间n的关系为：

un=jωζn+v0·ζn-n·(n·v0)ζn

(30)

把式(30)代入到式(29)中，可得：

n·(n·v0)ζn]dS

(31)

当边界面与平均流相切时，Eversman简化处理了式(31)，即：

(32)

式中，ζn为法向位移。

对于非滑移壁面，壁面上的背景流速为0，此时式(32)为：

(33)

对于如图1中所示的边界面，当与背景流相切时，可在式(33)的基础上进一步推导；当与背景流垂直时，需重新处理式(27)的等号右端部分。

(1)声激励边界

在消声器进口管的壁面上，如图1中Si所在区域，需要给定一个声激励计算整个声学域内的声学响应。边界面与背景流相切，当激励为法向位移时，有：

(34)

当激励为加速度时，a=-ω2ζ，则有：

(35)

(2)声阻抗边界

在面SR上，声阻抗Z0已知，壁面的法向位移与声压的关系为[11]：

jωZ0ζn=pa

(36)

把式(22)代入式(36)中，壁面上背景流速为0，得到位移与声速度势之间的关系，即：

(37)

把式(37)代入式(33)中，可得：

(38)

(3)穿孔声阻抗边界

假设穿孔处只有掠过流，通过流忽略不计，则式(33)依然成立。当穿孔部分掠过流速变化较大时，可以分段处理，假设每一段的平均流速相等。在图1所示的穿孔面Sp1和Sp2上，声压、声速度势、声质点法向位移、介质密度和形函数分别用p1、p2、φ1、φ2、ζn1、ζn2、ρ1、ρ2、N1和N2来表示。穿孔面之间的穿孔导纳记为ζp，穿孔面Sp1和Sp2上声质点法向位移与声压和穿孔导纳之间的关系为：

(39)

将式(39)中的ζn1和ζn2用p1和p2来表示，并代入到式(33)中，得：

(40)

(4)刚性壁面

刚性壁面上，如图1中Sw所在区域，背景流速和法向质点振速均为0。把式(22)代入式(27)的右端的积分中，有：

(41)

式中，vn=v0·n为边界面上的法向平均流的速度。

(5)无反射端

计算消声器的传递损失时，需将图1所示的出口面So设置为无反射端。有时在出口管的壁面设置为声阻抗已知，使反射声波被声阻抗壁面吸收，也是一种解决方案。如果分析的上限频率在出口管的平面波截止频率以下，则出口管内传递的只有平面波。本文从解析的角度推导无反射时出口面上声压和声质点振速之间的关系。

假设出口管为一段足够长的等截面直管，管道内流体介质沿轴线z方向以均匀马赫数M运动，并与出口管横截面垂直，管道内介质密度的变化忽略不计。管道内传递的声波为平面波，声速度势φ沿x和y方向的梯度为0，因此式(26)可简化为沿管道轴线的一维声传播方程，即：

(42)

式中，k0=ω/c0为波数。

式(42)的通解可写成如下形式：

φ=(C1e-jk0z/(1+M)+C2ejk0z/(1-M))

(43)

式中，C1和C2为待定系数。

无反射时，C2=0，则独立于时间项的声压p和法向声质点振速un可表示为：

(44)

把式(44)代入到式(27)等号右端，可得：

(45)

式(45)即为管道中平面波的无反射端的表达式。

2.2 离散化与矩阵装配

对于任意一种m节点的单元，其内部任意一点的场变量都可以用该单元上所有节点的场变量值来表示，声速度势则表示为：

(46)

式中：N为单元形函数组成的列向量，上标T表示转置，φi为单元节点i上待求的声速度势。

平均流速度的矩阵形式表示为：

(47)

把式(46)和(47)代入到式(27)的左端，并在声学域内Ⅰ和Ⅱ离散，用φ1和φ2分别表示区域Ⅰ和Ⅱ中的声速度势，则有：

(48)

式中:矩阵Lhs表示在域上的积分组装而成的矩阵，矩阵Si、Mi和Ci是由单元矩阵组装而成，即

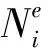
(49)

(50)

(51)

其中，

(52)

将式(48)～(52)进行组装，得到如下整体有限元矩阵表达式：

(53)

式(53)即为势流中声波方程的有限元矩阵表达式。由式(53)可知，伴流声场的FEM矩阵为非对称复矩阵。在实际的计算中，由于穿孔面的距离很窄，两个对应面面积大小很接近，因此可以从数值上把穿孔矩阵P处理成对称矩阵。所以其非对称性不是源于穿孔矩阵P，而是式(48)中体积分中由于流的存在得到的非对称矩阵Ci。相比有流状态，无流时的声学波动方程——亥姆霍兹方程，离散化后得到的对称非共轭的复矩阵，因此无流时声场的计算速度大概是有流时的两倍。

3 声学量计算

3.1 声压和质点振速

求解式(53)即可计算出每一个节点的声速度势φ，将声速度势代入到式(22)中便可计算出节点上的声压值，对声速度势求解梯度便可计算出声质点振速。通过坐标变换可知速度势对全局坐标的导数可由局部坐标表示，即：

[([N]′[Coord])-1[N]′]{φi}e

(54)

式中:[N]′为单元所有节点的形函数组成的列向量对局部坐标的导数组成的矩阵，[Coord]为单元所有节点的全局坐标组成的矩阵，{φi}e为单元的声速度势组成的列向量。

由式(54)可知，对于一个三维问题，必须将场变量置于体单元中才能计算出该变量的梯度。因此在计算横截面上声速度势的梯度时，首先需要找到该面单元所属的体单元，然后找到待求节点在体单元中的局部坐标，最后将局部坐标代入到式(54)中计算出声速度势的梯度。下面以如图2所示的四面体单元为例加以说明。

图2 一、二阶四面体单元节点及局部坐标系

图2中单元节点的局部坐标，如表1所示。

表1 四面体单元节点的局部坐标

找到面单元上待求节点在体单元中的节点编号，并以此在表1中找到其局部坐标，最后将点的局部坐标代入到式(54)中即可求解出该节点的声速度势梯度，进而计算出声压。

3.2 传递损失

传递损失定义为出口面为无反射端时，消声器的入射声功率级与透射声功率级之差，即：

TL=10lg(Wi/Wt)

(55)

式中:Wi为入射声功率，Wt为透射声功率。

如图1所示，在面S1计算入射声功率，在面So上计算透射声功率。由式(22)，声压p可表示为：

(56)

声质点振速在法向上的分量可表示为：

un=n·φ

(57)

式中:n为面的法向量，并约定其方向与声传播方向相同。

假设入射波为平面波，根据有流时平面波声压和质点振速的解析表达式，采用声波分解法，可以得到入口面上的入射声压pi和声质点振速ui的表达式为：

(58)

当管道内介质均匀沿着轴向流动时，沿管道轴向的声强I可表示为[12]：

(M|p|2/ρ0c0+ρ0c0|uz|2)]

(59)

式中,uz为声质点振速沿着管道轴向z方向的分量。

在面S1上，把式(58)代入到式(59)中便可得到任意一点的声强，并在面上积分，便可计算出入射声功率。在出口面So上，声学边界为无反射端，因此由式(53)计算出的面上节点的声速度势即为透射声速度势。将其代入式(44)中，即可计算出透射声压和透射声质点振速，代入式(59)计算出透射声强，并在面So上积分，得到透射声功率。把透射声功率和入射声功率代入到式(55)中计算出传递损失。

4 计算与分析

作为本文方法的验证和应用，本节使用自编的有限元法计算程序计算和分析干涉式消声器的声学性能，此类消声器是利用相位差产生声波的相互干涉，从而实现消声效果[1]。如图3所示的H-Q管是一种典型的干涉式消声器，由两条支路并联的管道组成，管道在第一个分叉点分成两条支路，在第二个分叉点处再合成一条。声波经过不同长度的管道产生了相位差，在第二个分叉点汇合处“相互干涉”实现了消声效果。分支管道内的气体流动直接影响两列声波间的相位差，从而影响共振频率和消声特性。

图3 Herschel-Quincke管

本文使用的H-Q管为圆形管道，其几何尺寸为d1=d2=0.05 m，l1=0.6 m。背景流场由CFD软件计算得到，当入口马赫数为0.1时，主管道与侧支管道的平均流速分别为30.61 m/s和3.61 m/s；当入口马赫数为0.2时，主管道与侧支管道的平均流速分别为61.92 m/s和6.7 m/s。参与计算的声学网格尺寸为4 mm，其流场信息通过CFD软件直接映射而来。

图4～6分别比较了无流、入口处马赫数为0.1和0.2时，使用一维平面波理论和三维有限元法计算得到的传递损失。H-Q消声器的传递矩阵可以在文献[1]中找到，此处不再赘述。此外，侧支管道处的端部修正对共振频率有较大的影响，使用一维理论计算时需要予以考虑。

图4 Ma=0时有限元法和一维理论计算结果对比

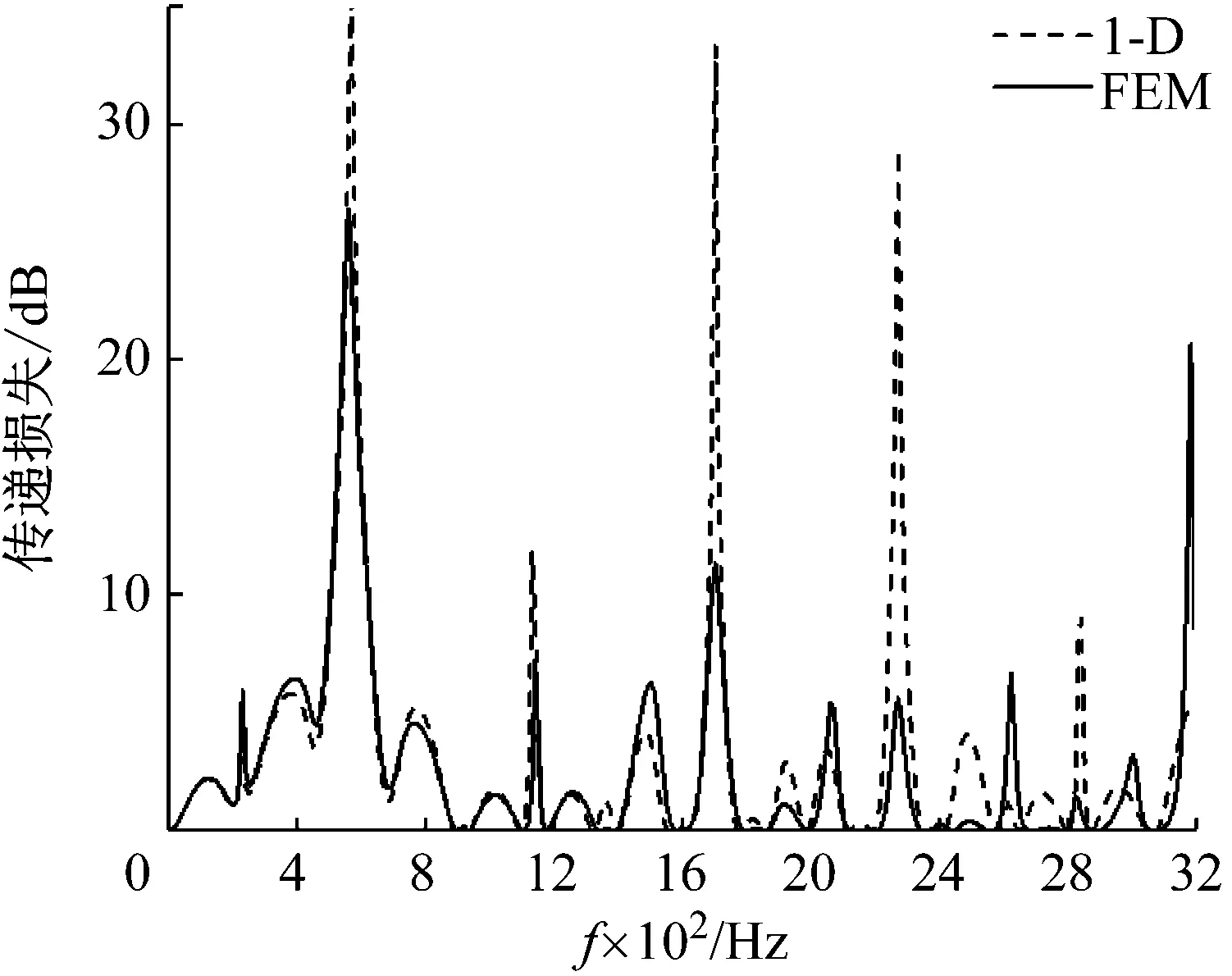
图5 Ma=0.1时有限元法和一维理论计算结果对比

图6 Ma=0.2时有限元法和一维理论计算结果对比

由图4～6可以看出，对于本文给定尺寸的H-Q管消声器，当入口处的马赫数分别为0、0.1和0.2时，一维理论与有限元法计算的传递损失大约分别在2 400 Hz、2 200 Hz和2 000 Hz以下吻合良好；高于这些频率，两种方法计算结果开始出现差异，这是因为在主管道和侧支管道的连接处的三维流场和三维声场效应所致，此时一维理论已不再适用。图3中A1和A2横截面上声压在2 200 Hz，马赫数为0.1时的声压的最大相位差分别为为0.036弧度和6.24弧度。A1面上的声压相位差极小，可认为是数值计算误差，因此A1上传递的是平面波。A2面上的声压相位差则是由两管交接处的三维波效应引起。

此外，进口处不同的马赫数所对应的平面波截止频率不同，截止频率随着马赫数的增加而减小，因而进一步缩减了平面波的适用范围。

图7显示了介质流动速度对H-Q管消声器传递损失的影响，这些数据来源于图(4)～(6)中有限元计算结果。介质流动改变了部分共振频率和通过频率，低频时部分无流时的共振频率和通过频率分别成为了有流时通过频率和共振频率；马赫数越高，传递损失在受到影响的通过频率和共振频率附近的变化越大；在中高频，介质流动对消声性能的影响非常明显。

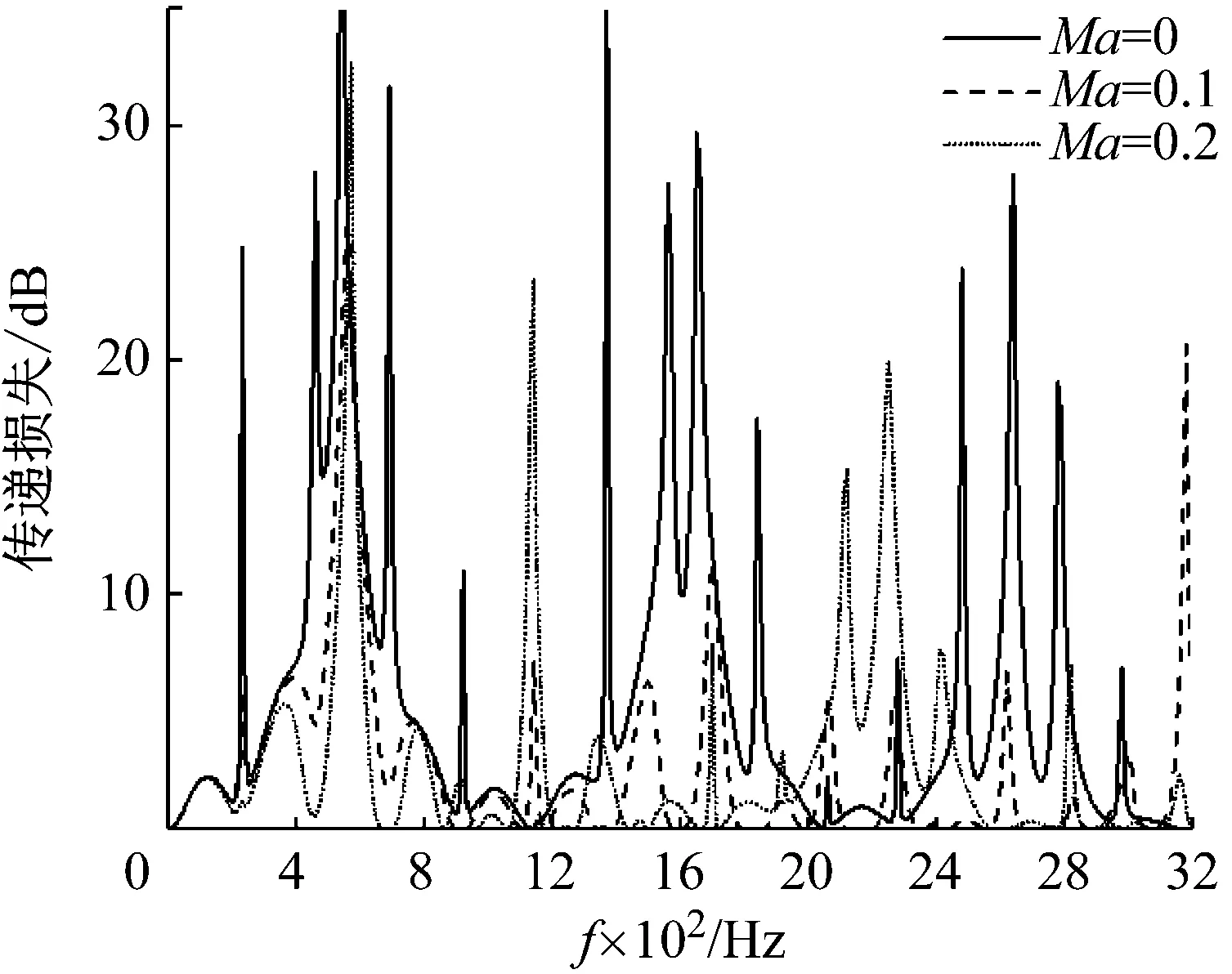
图7 马赫数对传递损失的影响

接下来研究结构改变对H-Q管消声性能的影响。H-Q1即为图3所示的结构；H-Q2的结构如图8所示，包含了两个旁支管，其中d1=d2=d3=0.05 m，l1=0.6 m，l2=0.3 m；H-Q3的结构如图9所示，主管中增加一个简单膨胀腔，其中d1=d2=0.05 m，d3=0.15 m，l1=0.6 m，l2=0.3 m。

图8 H-Q2管

图9 H-Q3管

图10给出了三种H-Q管消声器传递损失的计算结果。可以看出，结构的改变明显影响了H-Q管的消声特性，特别是共振频率。H-Q2因为包含了两个旁支管，所以传递损失中共振峰的数量多于H-Q1，并且共振峰向低频方向移动，提升了低频段的声学性能。H-Q3主管道增加了一个简单膨胀腔，使得整个频段上共振峰的数量增多，从而改善了多数频段内的消声性能。

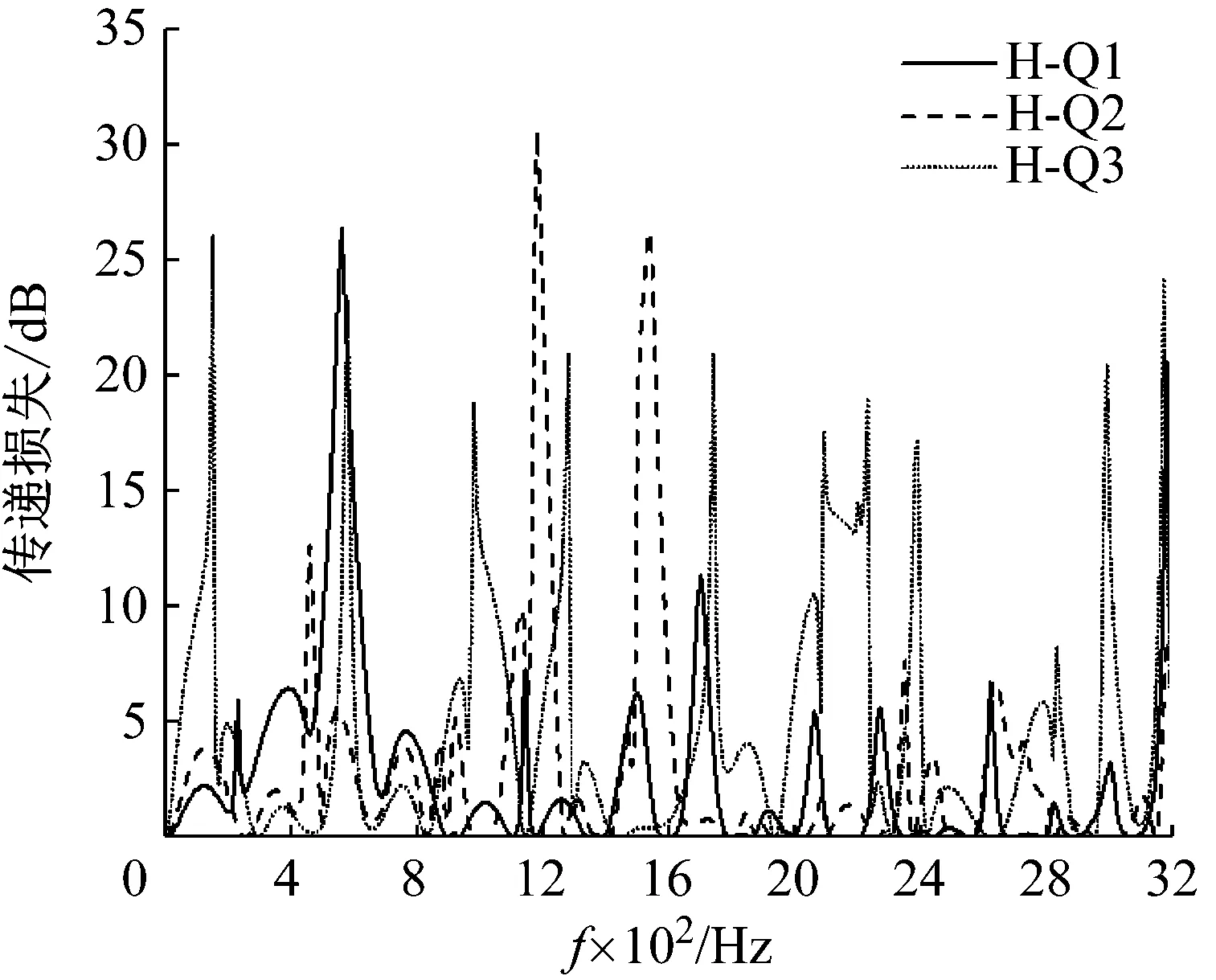
图10 结构改变对H-Q消声器的声学性能的影响

5 结 论

本文推导了势流中的声波方程，应用伽辽金加权余量法建立了有限元的弱形式表达式。针对管道声学的计算，讨论了所需边界条件的处理方法，通过离散和装配得到了有限元矩阵方程。自行编程实现了推导的有限元算法，计算和分析了介质流动速度和结构形式的改变对H-Q管消声器声学性能的影响。结果表明，当入口处的马赫数分别为0、0.1和0.2时，一维理论与有限元法计算的传递损失大约分别在2 400 Hz、2 200 Hz和2 000 Hz以下吻合良好；高于这些频率，两者的计算结果开始出现较大的差异，这是由于主管和支管交界处的三维流场和三维声场效应所致，此时一维方法不再适用。马赫数越高，平面波截止频率越低，一维理论适用的频率范围越窄。介质流动影响H-Q管消声器的声学特性，特别是在共振频率和通过频率附件，马赫数越高，影响越显著。具有两级的H-Q管，共振峰数量增多，共振频率降低。主管道包含了简单膨胀腔的H-Q管，共振峰的数量增多，从而提升了在多数频段内的消声性能。