大跨平屋盖风荷载特性及风压预测研究
2021-02-07陈伏彬唐宾芳蔡虬瑞李秋胜
陈伏彬,唐宾芳,蔡虬瑞,2,李秋胜
(1.长沙理工大学 土木工程学院,长沙 410114; 2.中国能源建设集团湖南省电力设计院有限公司,长沙 410007;3.香港城市大学 建筑与土木工程系,香港 999077)
大跨屋盖结构能够提供更大的无柱空间,已广泛应用于体育场馆、机场航站楼、展览中心等,同时由于其具有跨度大、质量轻、阻尼小等特点,风荷载已成为此类结构设计的主控荷载之一[1]。由于结构的特殊性,现有的结构荷载规范未能给出准确的风荷载数值,往往通过刚性模型测压试验获得其设计风荷载。虽然同步多点压力扫描系统(Synchronous Multi-Pressure Scanning System,SM-PSS)的应用大大增加了同步采集的数据容量,大跨屋盖结构面积一般都很大,往往在100 m2的面积上仅布置1个风压测点,风压测点远少于大跨屋盖结构的有限元节点数,给精细化的大跨结构抗风设计带来诸多不便。如何将有限测点上的风压数据扩展到能够满足结构有限元分析的更多节点上是目前亟待解决的问题。因此,基于已有的风压数据对未知测点风压预测很有尤显重要。
本征正交分解(Proper Orthogonal Decomposition,POD)技术作为一种数据压缩和特征值萃取工具,首先被Armitt引入到风工程领域[2],该方法是一种应用广泛的数据降维方法,可以将脉动风压场分解为仅依赖时间的主坐标与仅依赖空间的本征模态的线性组合,是分析随机风压场的有效工具。通过对未知测点本征模态的预测,并将预测的模态与主坐标相乘累加,就能得到未知测点的风压时程[3],广泛应用于低矮建筑[4-5]、大跨结构[6]、高层建筑[7]与桥梁结构[8]的脉动风荷载及风致响应的重构研究中,并根据已知测点的特征向量利用插值法获得未知位置的特征向量来预测风压序列[9-10]。
空间数据插值,就是通过一组已知的离散数据或分区数据,根据某种数学关系推求出其它未知点或者未知区域的数学过程。空间内插法分类的方法较多,如可依据确定或随机划分、全部或局部划分、点与面划分等标准分类。根据其数学本质与基本假设的不同,又可分为随机模拟法、统计插值法、空间统计插值法、几何插值法以、函数插值法、神经网络学习法等。人工神经网络(Artificial Neural Network,ANN)因其具有良好的非线性映射能力,被广泛应用于各领域的插值问题。在结构风工程领域,神经网络方法已成功预测了大跨屋盖结构[11]、低矮双坡屋面[12-13]、折叠网壳结构[14]等结构的风压分布特性,并取得了较好的预测精度。
本文结合本征模态分解法(Proper Orthogonal Decomposition,POD)的降维技术与BP神经网络强大的学习功能,提出一种适用于大跨屋盖结构风压重构与预测的技术方法,并采用某一大跨平屋盖刚性模型试验数据验证其有效性。
1 基本理论
1.1 POD法
POD提供了对于复杂的随机过程只用少量的前几阶本征模态提取本质特征的有效途径。其主要目的是获得本征函数φn(x,y),它和随机脉动风场的全体元素有很好的相互关系。本征正交分解原理的推导有多种途径,如:投影极值原理、瑞利商方法(Rayleigh Quotient)、Karhunen-Loeve分解定理,均推导出同样的结果。
假设由风洞实验获得的建筑物表面各测点零均值脉动风压时程为各态遍历一个随机过程,表示为:
p(t)={p1(t),p2(t),…,pN(t)}T
(1)
本征正交分解的目标是最大化投影方差,即寻找一组向量空间,使脉动风压向量在这组向量空间上的投影最大化。那么对于风压场来说,存在如下本征值问题:
CΦ=ΛΦ
(2)
式中:C=E(p(t)p(t)T)为脉动风压的零时滞协方差矩阵,本征值对角矩阵Λ=diag(λ1,λ2,…,λN),本征模态矩阵Ψ=[φ1,φ2,…,φΝ],二者按降序排列。
通过本征正交分解后空间(x,y)位置测点的风压时程可由模态扩展表示为:
(3)
式中:M为扩展的本征模态数,φn(x,y)为归一化且相互正交的本征模态,an(t)为时间主坐标,由下式确定:
(4)
易证明重构后的脉动风压均方差值为:
(5)
由此可知,本征值λn能够反映第n阶本征模态对脉动风压均方差的能量贡献量,并可根据前m阶模态所占累计能量比EM来确定扩展模态数M,其值为:
(6)
1.2 BP神经网络
BP神经网络[15]是一种以误差反向传播为基础的多层前馈网络,其网络拓扑结构由三部分组成:输入层、隐含层和输出层,其中隐藏层可以是多层的。BP神经网络算法由输入信号的向前传播与误差信号的反向传播两个过程构成,正向传播时,数据从输入层经隐含层逐层向后传播,若输出层得不到期望的输出,则转至误差信号的反向传播,再由误差根据梯度下降法向后传播逐层修改权值与阈值,使误差减小,反复进行,直到误差不再下降,停止训练。
在信号的向前传播阶段,隐藏层中第i个神经元的输入等于输入信号的加权和,并通过非线性函数传递,则第i个神经元的输出为:
(7)

Δω=学习率η·局部梯度δ·上一层输出信号v
(8)
2 风洞实验简介
风洞试验模型采用有机玻璃制成,缩尺比为1∶150,模型几何尺寸为40 cm×40 cm×20 cm,满足阻塞率小于5%的要求。风洞实验模型见图1。
在模型上表面布置了测点256个,内表面布置测点180个,并在模型屋盖右下角区域进行了测点加密布置。测点布置及风向角定义见图2。在边界层风洞中精确模拟了B类地貌风场条件,风场参数,如图3所示。

图2 测点布置及风向角示意图

图3 风洞试验风速和湍流度剖面
本文选取屋盖表面A区测点为研究对象,并假设空心测点○为信息缺失的点,运用POD-BPNN方法预测其风压时程,并通过与风洞实验数据对比验证此方法的有效性。
3 风荷载特性分析
3.1 数据分析
在风洞实验中测得建筑物表面上测点的净风压力pi(t),再将此压力pi(t)除以建筑物远前方上游来流风的平均动压,得到一个量纲为一的系数cpi(t),称为此测点的风压系数,如公式(9)所示。模型试验中符号约定以压力向内(压)为正,向外(吸)为负。屋盖表面各点的风压系数由下列公式给出:
(9)
式中:cpi(t)是试验模型上第i个测压孔所在位置的风压系数,pi(t)是该位置上测得的表面风压值,p0和p分别为参考点处测得的平均总压和平均静压。对于悬挑的位置(上下对应布置两个测压孔),由上下表面对应的测压点测出的压力相减得到:
(10)

采用相关系数R来评价本文方法的预测结果,其表达式为:
(11)

3.2 风压特性分析
图4、5分别给出了0°与45°风向角下屋盖上表面的平均风压系数和脉动风压系数分布。从图4可以看出,当气流垂直于屋盖边缘时,在边缘发生明显的分流并产生柱状涡,在边缘区风压系数达到-1.05;在斜风45°来流工况下,气流在角部发生分离,形成锥形涡,并在这种特征湍流作用下产生明显的高负压,负风压系数达到-1.84。从图5中可以发现,脉动风压分布与平均风压分布具有相类似的趋势。

(a)0°

(a)0°
4 风压预测
4.1 表面风压Pod特性分析
表1列出了2个风向角下屋盖A区各阶模态对脉动风压的贡献情况,可以看出,前10 阶模态对脉动风压的累计贡献达到了80%,而前20阶模态包含了90%以上的能量,且45°风向角比其他风向角能量累计更快,这可能与A区测点处于45°风向角下迎风前缘有关。

表1 特征值累积贡献比例
4.2 脉动风压时程的预测
为验证POD-BPNN方法预测脉动风压时程的有效性,对0°与45°风向角下空心测点°进行了脉动风压的预测,选取A区实心测点•为已知测点并通过POD法计算本征向量与主坐标,根据测点的空间坐标关系对未知测点本征模态进行插值,再利用式(3)来计算未知测点的脉动风压时程。利用BP神经网络预测未知测点的本征模态时,以测点坐标向量(x,y)为输入参数,未知测点的本征模态作为输出结果,实心测点•的本征真模态作为训练数据。根据已有文献的网络模拟经验[9],选择具有两个隐含层的神经网络模型,两个隐含层层数分别为15和10,因此网络结构表现为2-15-10-1,各参数具体取值如表2所示。预测的具体步骤,见图2。

表2 BP神经网络参数
表3给出了0°与45°风向角下基于POD的BP神经网络方法对脉动风压的预测结果,限于篇幅,这里只给出了部分测点的预测结果。从表3中可以看出,BP神经网络方法预测的均方根误差较小,证明BP神经网络方法是一种可靠的插值方法。从整体而言,平均风压预测在风压值大小和相关性都能达到很好的效果;而对于脉动风压而言,位于气流分离区的测点预测结果相对较好、相关性强,位于尾流区部分其相关性则相对较弱(如测点56、76、96)。
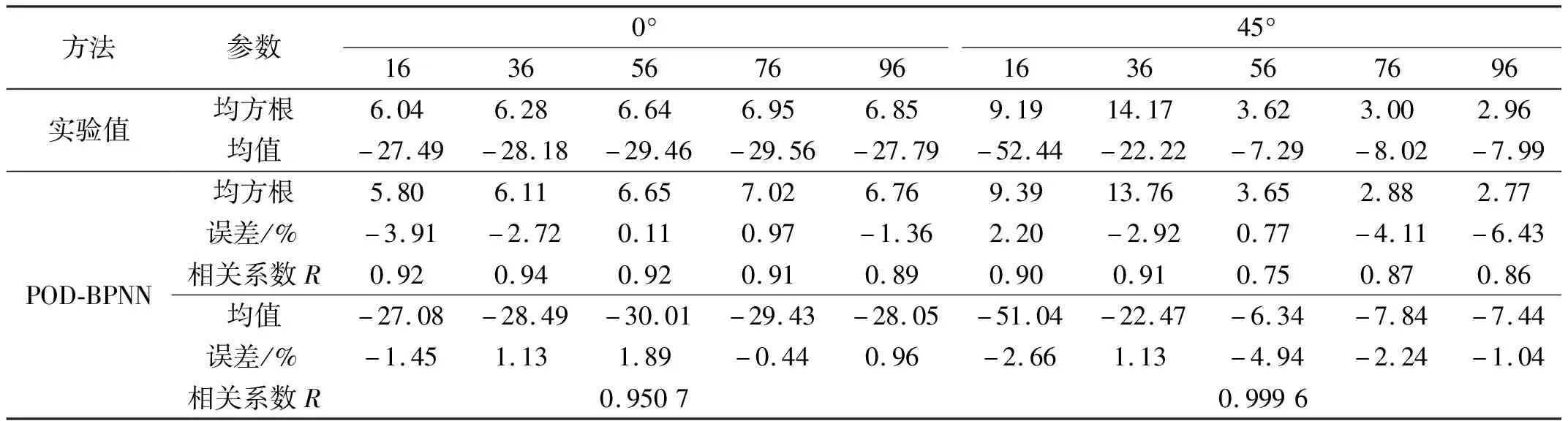
表3 预测结果对比
图6、图7分别给出了0°和45°风向角下POD-BPNN方法预测的风压时程与实验风压时程对比。从图6、图7可以看出,除45°风向角下56号测点时程值曲线与实验值吻合度较差,笔者认为主要原因是测点位于气流尾流区;其它测点所预测的脉动风压时程曲线与实验结果较为一致,瞬时峰值点风压也能较好的符合实验值。
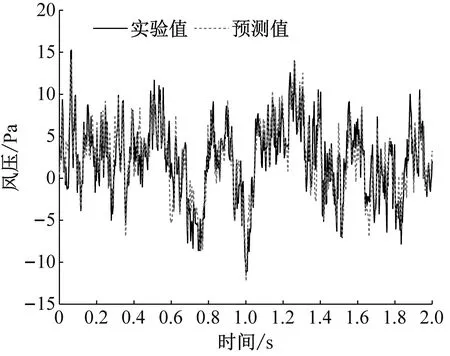
(a)测点16
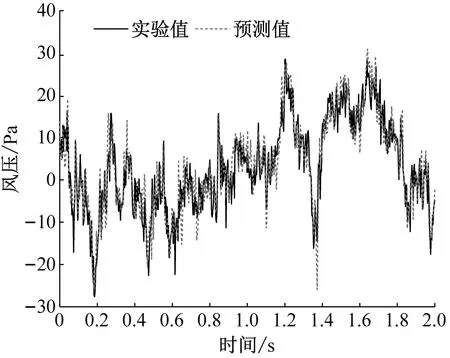
(a)测点16
图8、图9分别给出了2个典型测点在0°与45°风向角下预测的脉动风压归谱一化功率曲线。从图8、图9可以发现POD-BPNN方法所预测的脉动风压功率谱曲线与实验的结果较为吻合,其峰值误差最大为9.8%。

(a)0°

(a)0°
5 结 论
本文研究了大跨平屋盖结构风压特性,并结合本征正交分解法与BP神经网络方法预测出了大跨度开合屋盖测点的脉动风压时程,并与风洞试验结果进行了有效对比,得出以下几点结论:
(1)大跨平屋盖结构在迎风前沿产生负风压,特别是下斜风作用下,受到特征湍流的作用,在边缘及边角区域产生高负压。
(2)POD是一种有效的降维方法,通过POD分解,对与空间有关的本征模态进行预测,并与时间主坐标相乘累加即可获得较高精度的预测结果。
(3)通过训练BP神经网络来拟合POD本征模态的非线性关系,将预测的本征模态与时间主坐标相乘累加得到风致时间序列,得到了可靠的预测结果;不论是来流垂直于迎风边缘,还是45°斜风作用下,其平均风压预测误差小于5%,脉动风压误差小于7%,表明该POD-BPNN法可以有效用于大跨结构表面风压的预测。
(4)对于迎风的边角区域,其风压复杂,需要增加测点的数量以获得更高的预测精度。
