阵列式平台漂浮式风电场Spar平台动态响应及稳定性改进研究

2021-02-07岳敏楠李蜀军

振动与冲击 2021年3期

岳敏楠，王博，李春,2，李蜀军

(1.上海理工大学能源与动力工程学院，上海 200093；2.上海市动力工程多相流动与传热重点实验室，上海 200093)

“由陆地向海洋、由固定基础向漂浮式平台”是未来风电发展的主要方向已为学术和风电企业所共识[1]。漂浮式风力机在役环境复杂多变，在役期间需承受海风、海浪、海流甚至地震、浮冰等多种载荷作用，即便仅考虑海风、海浪对平台和安装在其上面的风力机的作用，整个问题都是复杂的风波耦合问题[2-3]：① 当波浪载荷引起平台运动时，风力机机舱也随之运动；② 风力机机舱的运动又引起流入风力机风轮风量的改变；③ 风轮流入风量的改变会引起风轮载荷的变化。载荷的变化通过风轮、机舱、塔架又会传递到平台，从而影响整个漂浮式风力机系统的运动。同时平台的转动也会影响风力机风轮的载荷和气动特性。由于平台的运动，将引起作用在风力机上的风速波动进而导致输出功率的波动，这是海上风电机组浮式基础结构设计的最大挑战。平台的稳定是漂浮式风力机安全运行的根本保障，因此，研究外界环境条件作用下漂浮式风力机平台的动态响应特性具有重要的意义。

现阶段，根据获取稳定性方式的不同可将漂浮式平台分为四大类：张力腿式平台(Tension Leg Platform,TLP)、单柱式平台(Spar)、驳船式平台(Barge)和半潜式平台(Semi-Submerisible)[4-5]。保持这些不同结构形式平台的稳定性主要为张力筋腱的预张力、悬链线及压载自重所提供的回复力和水线面的面积矩，而在实际应用中一般是上述三种方式的组合。截止到目前，国内外学者对漂浮式风力机平台开展了大量研究，研究方法主要包括波浪水池试验[6-10]和数值仿真[11-16]两种，前者主要侧重于漂浮式平台的运动响应测试、验证数值仿真方法的准确性及漂浮式风力机概念模型的合理性方面。采用水池试验方法虽准确可信，但其成本较高，即便采用比例缩尺方法，考虑到尺度效应，漂浮式风力机整机模型也无法无限缩小，这增大了试验的难度，对试验设备要求也比较高。此外，绝大多数科研院校与研究机构不具备试验水池，极大的限制了漂浮式风力机平台动态响应特性的水池试验研究。因此，现阶段对于漂浮式风力机平台的研究以数值仿真为主，采用数值仿真方法研究内容主要侧重于载荷激励下漂浮式风力机平台的动态响应以及探索如何有效提高漂浮式风力机平台稳定性方面。

目前提高漂浮式风力机平台的稳定性主要通过主被动结构控制[17-20]、叶片变桨距技术[21-23]、对平台主体改进设计[24-25]和采用新型系泊系统四种方法[26-27]。结构控制所需TMD质量块质量较大，这无疑增大了成本，且增加了前期安装的难度，主动结构控制所需控制力巨大，并不适合于漂浮式风力机平台的稳定性控制。叶片变桨距控制技术虽可在一定程度上提高漂浮式风力机平台的稳定性，但会加剧叶根疲劳载荷，且所需控制策略较为复杂。对平台主体改进设计和采用新型系泊系统两种方法虽然有一定效果，但其研究方法均存在一定的缺陷，且研究对象始终局限于单个漂浮式风力机平台，并未对彼此之间存在耦合效应的多座漂浮式风力机平台进行研究。文献[28]借鉴赤壁之战”铁索连舟”增强船舶稳定性的思路，首次提出了共用系泊系统多平台阵列漂浮式风电场的设计方法并建立了3×3阵列Spar平台漂浮式风电场，研究了风波流作用下漂浮式风电场Spar平台的动态响应特性，但其存在的问题在于：① 仅仅分析了平台的纵荡、垂荡、纵摇响应，并未研究平台的首摇、横摇响应，事实上，当采用阵列方式建立漂浮式风电场时，位于最外侧平台的系泊系统势必不对称，不对称的系泊将导致不对称的受力，进而导致不对称的系泊回复力矩，因此，风电场中平台的首摇、横摇响应亦是不可忽略的运动特征参数；② 气动载荷的求解属弱耦合求解，求解精度较低因而计算结果准确与否有待考证。

本文借鉴上述研究经验，首先基于叶素动量理论考虑叶尖损失、轮毂损失以及动态失速通过对AQWA二次开发建立了漂浮式风力机气动-水动-系泊耦合模型并实现了模型算法求解，其次研究了3×3阵列漂浮式风电场Spar平台的首摇、横摇响应，针对平台存在的首摇、横摇响应过大问题提出了两种提高漂浮式风电场Spar平台首摇、横摇稳定性的措施，以期为漂浮式风电场的建造及安全性的提高提供理论参考。

1 研究对象

研究对象为基于Spar平台的漂浮式风力机，风力机为NREL 5 MW风力机[29]，平台为OC3-Hywind Spar[30]，风力机参数见表1，平台参数见表2。基于风力机、平台几何参数建立Spar平台漂浮式风力机整机模型,如图1所示。

表1 NREL 5 MW风力机参数

表2 OC3-Hywind Spar平台参数

图1 Spar平台漂浮式风力机

一般而言，为避免上游风力机尾迹对下游风力机气动性能的影响，水平轴风力机间距：前后约7D～8D[31]，左右约3D～5D[32](其中，D为风轮直径)，但①海上风资源风速与主风向相对稳定、湍流度较低，因此海上风力机运行时尾迹影响相对较小；② 不涉及风力机气动性能、尾迹方面研究，因此，所提出漂浮式风电场中风力机间前后、左右间距均为500 m。鉴于此，建立了3×3阵列Spar平台漂浮式风电场，如图2所示。系泊系统由两部分组成：固定悬链线和链接悬链线，具体参数,见表3。

图2 3×3阵列Spar平台漂浮式风电场

表3 漂浮式风电场系泊系统

2 研究方法

现阶段，基于数值仿真方法对漂浮式风力机平台动态响应特性的研究大都基于两种途径：① 基于传统的海洋工程水动力软件，包括WAMIT、AQWA、Hydrostar及MOSES等；② 基于专业的风力机仿真软件，包括FAST、GHBladed、FLEX5、HAWC2等。上述两种途径存在的问题在于：

(1)诸如AQWA、WAMIT等的海洋工程水动力软件虽具有成熟、完备的水动力求解模型，但其气动载荷求解模型比较简单。国内外学者采用上述海洋工程水动力软件进行研究时，风载荷一般简化为定常的轴向推力、或直接采用FAST求解的风轮推力作为外部激励、或采用风压模型求解。事实上，波浪载荷激励导致的漂浮式风力机底部平台六自由度运动将诱发上部风轮的俯仰运动，将对来流相对风速产生影响，意味着即使在定常风工况下，气动载荷实际上也是非定常的。因此，简化为定常轴向推力的研究方法在气动方面是不准确的；FAST求解所得的风轮推力虽然能够真实反映风力机气动载荷特征，但每个时间步的推力大小与上部风力机的运动规律不相吻合，风波等外部载荷激励下的漂浮式风力机平台的动态响应具有强非线性特征，底部漂浮式平台的运动将诱发上部风轮的运动，这将导致来流相对风速的变化，进而影响气动载荷，气动载荷的变化又影响到平台的运动形式，平台水动力载荷与平台运动形式相关，因此直接导入FAST所求解的非定常风轮推力、忽略漂浮式风力机平台真实运动形式的研究方法是不严谨的。

采用风压模型求解风载荷时，风载荷大小仅与“平台与来流风速”相对速度的平方项正相关，意味着相对风速越大风载荷越大，而在风力机的实际运行中，当超过额定风速时，由于风力机的变桨距控制，风轮推力是逐渐减小的，因此采用风压模型求解风载荷的研究方法亦是不准确的。

风力机气动载荷的求解主要包括基于N-S方程的计算流体力学方法(CFD)、涡尾迹方法和叶素动量理论(Blade Element Moment Theory，BEM)。CFD方法能够精确的求解风力机气动性能，能够详细的捕捉叶片周围流体的流动特性与细节，可开展流场中速度场、压力场和涡量场等流动参数的分析，是研究和分析相关问题流动机理的基础。但由于风力机叶片的复杂性，网格划分方面存在的诸多难点，同时对网格数量等要求较高。此外，湍流模型的选取、边界条件的设定等均会影响计算结果。更为重要的是现代漂浮式风力机不仅尺度大，且求解区域存在多尺度问题，因此通过CFD计算获得气动载荷就目前计算机能力和数值计算方法无法实现。涡尾迹方法，虽然计算精度不如CFD，但其能够精确的求解气动力沿风力机叶片的详细分布，亦能够再现风轮涡尾迹结构，但对漂浮式风力机平台动态响应的研究而言，仍然存在求解公式过于繁琐复杂的缺点。较之涡尾迹方法和CFD方法，叶素动量理论具有理论模型简洁直观、计算快速等优点，且国内外学者针对其局限性已发展了较为丰富的修正处理方法。因此，现阶段叶素动量理论仍是风力机叶片气动载荷的主要计算手段。对于漂浮式风力机平台动态响应的研究而言，本质需求在于快速、高效求解气动力，因此叶素动量理论优势最为明显。

(2)诸如FAST、Gblade等的风力机仿真软件基于叶素动量理论考虑各种损失虽建立了较为精确的气动载荷求解模型，但水动力载荷的求解通过调用WAMIT等水动力软件求解的线性水动力系数；此外，相关学者开展研究时，悬链线系泊张力的求解大都通过静态悬链线理论，静态悬链线方程求解系泊张力时忽略了平台与系泊系统的耦合作用、同时也忽略了环境载荷所产生的动力效应；更为关键的是，FAST仅能求解外界载荷激励下单个漂浮式风力机平台的动态响应特性，无法考虑平台间存在耦合效应的多个漂浮式风力机平台的动态响应研究。

因此，本文基于叶素动量理论采用Fortran编程编译dll动态链接文件，实现对水动力软件AQWA的二次开发，建立了漂浮式风力机气动-水动-系泊耦合模型以及建立了共用系泊系统多平台阵列漂浮式风力机气动-水动-链接系泊-固定系泊耦合动力学模型，并实现了上述两种模型算法的求解。

具体处理方法如下：

2.1 气动载荷及其可靠性验证

将轮毂中心速度作为脉动风速与来流风速在每个求解时间步进行叠加，基于BEM理论求解气动力，NREL 5 MW风力机叶片基于5个DU系列翼型和1个NACA系列翼型设计而成，共17个截面(包括叶根附近两处圆形截面)。叶片各截面翼型几何参数见表4。迭代求解轴向、切向诱导因子以及推力和扭矩时需要调用各截面翼型升阻力系数。因此，采用Xfoil获得小攻角时各截面翼型的升阻力系数，并进一步外推到-180°～180°，计算时可直接被dll文件调用。各截面翼型的升阻力系数如图3所示。风力机在实际运行时由于叶片旋转将产生动态失速，导致叶片截面上的升力系数远大于静态翼型的升力系数，采用Du-Selig失速模型对叶片动态失速区叶素的升阻力系数进行修正。低于额定风速时，风力机无需变桨，当超过额定风速时，风力机通过变桨策略达到卸载的目的。本文参照Jonkman所提供NREL 5 MW风力机不同风速下的设计桨距角[33]，如图4所示。根据来流风速进行线性插值获得当风速超过额定风速时的桨距角从而实现对风力机的变桨控制。

表4 NREL 5MW风力机叶片各截面几何参数

图3 翼型升阻力系数

图4 NREL 5 MW风力机叶片设计桨距角

为验证本文气动载荷程序的可靠性，特将不同风速下本文风轮推力计算值与FAST风轮推力计算值进行对比，如图5所示。由图5可知，本文风轮推力计算值与FAST风轮推力计算值吻合度较高，可验证本文气动载荷计算所用程序的可靠性。

图5 风轮推力计算值对比

2.2 波浪载荷求解、网格划分及可靠性验证

波浪载荷求解主要有两种方法：莫里森方程和基于势流理论的辐射/绕射理论。前者主要求解作用于小尺度结构的波浪力，将波浪力视为惯性力和拖曳力两项的叠加，即分别与流体加速度、速度的平方项相关，忽略结构对波浪的绕射效应；后者主要用于求解作用于大尺度结构的波浪，忽略流体的黏性效应，可考虑结构对波浪的绕射效应。本文研究对象Spar平台主体特征长度9.4 m，一般情况下，对入射波浪的绕射效应不可忽略，因此波浪载荷求解采用基于势流理论的辐射/绕射理论。

波浪运动属流体运动的一种，对于绝大多数波浪运动，可认为海水无粘性且不可压缩，因此波浪运动满足连续性方程和欧拉运动方程。势流理论假定流体无旋有势，即存在速度势函数满足拉普拉斯方程，表明波浪运动为不可压缩有势流动。速度势函数应同时满足：① 海底不渗透边界条件；② 物面边界条件；③ 自由液面运动边界条件；④ 自由液面动力边界条件；⑤ 无穷远处辐射边界条件。通过给定初始波面条件，即可求解速度势函数，进而可求解整个波浪场的速度分布，根据线性化的伯努利方程，即可求解整个波浪场的一阶线性水压强分布，通过对浮体湿表面面元的压强积分即可求解作用于浮体湿表面的一阶水压力，此为一阶波浪激振力。

波浪载荷求解需要对浮体湿表面进行面元离散，即需要网格划分。网格划分结果如图6所示，绕射单元总数约2 500，非绕射单元总数约1 500。为验证网格划分能否满足水动力计算精度的需求，采用近场法、远场法两种方法对纵荡二阶平均漂移力进行求解，当两种解法的结果趋势一致、量级接近时，可认为网格划分能够满足水动力计算精度的需求，求解结果如图6所示。之所以通过对平台纵荡二阶平均漂移力的求解判断网格划分是否满足水动力计算精度的需要，是因为近场法通过对湿表面的压强积分求解二阶波浪力，该方法依赖网格划分，而远场法通过求解动量方程获得纵荡二阶平均漂移力，该方法不依赖网格划分，远场法求解精度较高。因此，当二者求解结果接近时，可认为网格划分能够满足水动力计算精度的需求。

图6 网格划分

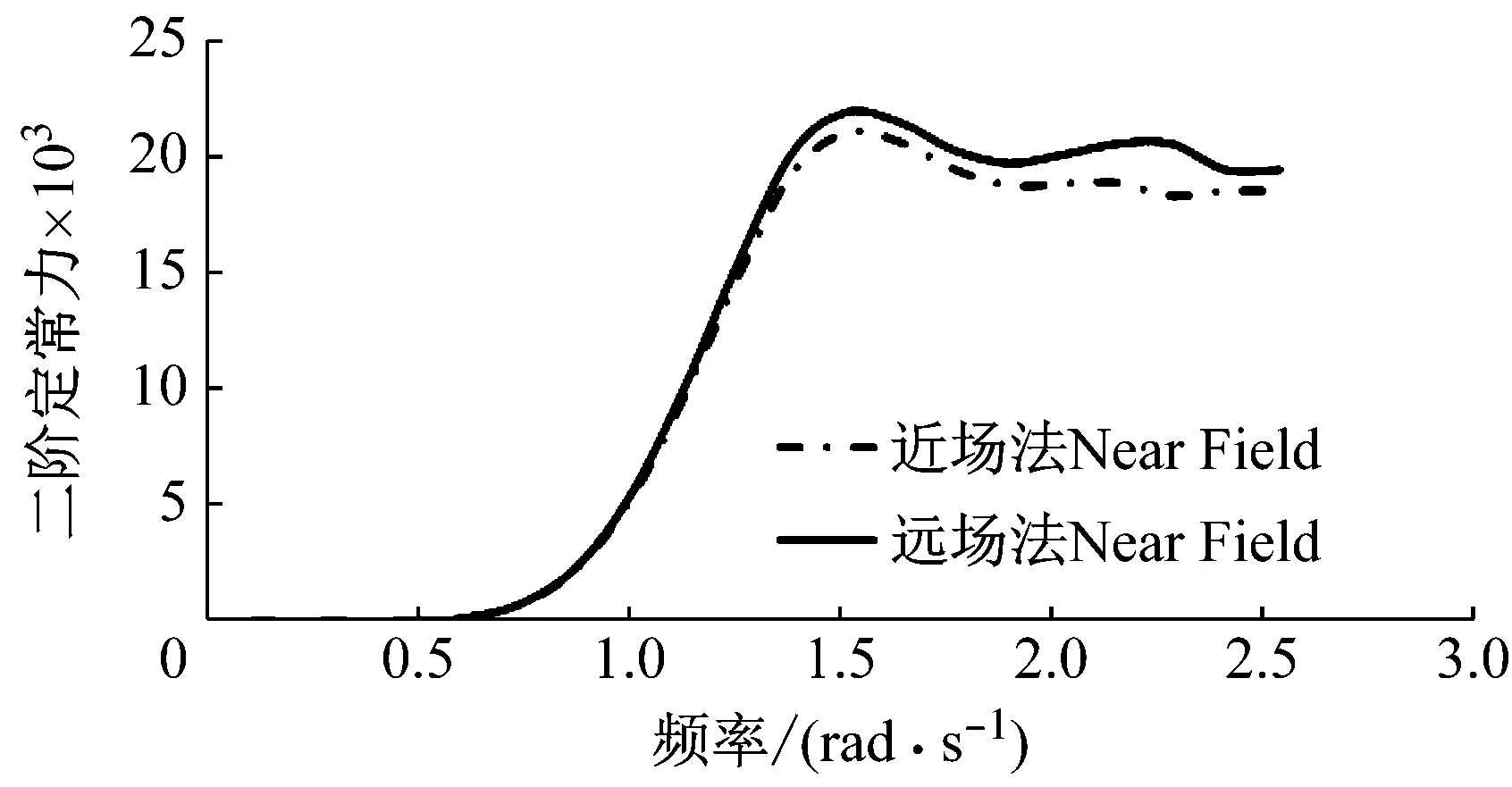
图7 纵荡二阶平均漂移力

2.3 控制方程及运动自由度

前文已说明，为最终求解波浪载荷需已知初始波面边界条件，相应的就产生了不同的波浪理论。如线性微幅波浪理论、Stokes波浪理论、椭圆余弦波浪理论和孤立波浪理论，不同的波浪理论适用条件不同，例如，孤立波浪理论适用于水深极浅水域。本文研究对象漂浮式风力机作业于上百米的水深海域，入射波高、波长相对于水深均为小量，因此本文采用线性微幅波浪理论。线性微幅波浪作用下，漂浮式风力机平台亦跟随波浪频率作简谐运动，其在波浪场中的运动可视为具有质量、刚度和阻尼的系统做简谐振动。根据势流理论和辐射/绕射理论，可最终求解不同频率单位入射波浪作用下平台的附加质量系数矩阵、辐射阻尼系数矩阵及其六自由度幅值响应算子(Response Amplitude Operator，RAO)。

气动载荷基于叶素动量理论考虑叶尖损失、轮毂损失及动态失速求解。对于波浪载荷，首先基于辐射/绕射理论可求解一阶、二阶波浪载荷的频域解，其次对线性传递函数、二次传递函数作傅里叶逆变换求得脉冲响应函数，最终根据脉冲响应函数和波高的双重卷积求解时域波浪载荷。基于上述建立了风波作用下单个漂浮式风力机平台的运动方程：

(M+M()

Fwind(t)+Fwave(t)+Fmooring(t)

(1)

式中:M为平台质量矩阵；M()为无限大频率时平台附加质量矩阵；C为平台辐射阻尼矩阵；K(s)为平台净水刚度矩阵；R(t)为速度脉冲响应函数矩阵；Fwind(t)、Fwave(t)、Fmooring(t)分别为时刻t六自由度的风载荷、波浪载荷及系泊系统回复力；分别为t时刻平台的位移、速度及加速度。

不同于单个漂浮式风力机平台在外界载荷激励下的运动，所提出的多平台阵列共用系泊系统漂浮式风电场平台的运动不仅涉及风-波-系泊耦合效应，亦包括因平台之间的系泊链接导致的平台与平台之间的耦合运动，因此其运动形式更为复杂。所提出的漂浮式风电场系泊系统由悬链线构成，包括固定悬链线和链接悬链线，对于仅与链接悬链线链接的平台，其受到的固定悬链线作用力/力矩为0，对于与固定悬链线、链接悬链线均链接的平台，其在每一时刻均受到固定悬链线、链接悬链线作用力/力矩，链接相邻平台的链接悬链线在每一时刻具有力的传递，导致相邻平台之间的运动具有耦合效应。外界载荷激励下，考虑固定悬链线、链接悬链线回复力导致的平台与平台之间的相互作用，基于上述建立了漂浮式风电场平台时域运动方程组：

(2)

式中:Mn为第n个平台的质量矩阵；Mn()为第n个平台无限大频率时系统附加质量矩阵；Cn为第n个平台辐射阻尼矩阵；Kn为第n个平台净水刚度矩阵；Rn(t)为第n个平台速度脉冲响应函数矩阵；Fn-风(t)、Fn-浪(t)、Fn-链接(t)、Fn-固定(t)分别为时刻t作用在第n个平台六自由度的风载荷、波浪载荷、海流载荷、链接悬链线作用力/力矩、固定悬链线作用力/力矩；分别为t时刻第n个平台的位移、速度及加速度。

风波作用下，平台六自由度运动包括沿x轴、y轴和z轴的平动及绕各轴的转动，如图8所示。平动包括纵荡(Surge)、横荡(Sway)和垂荡(Heave)，转动包括横摇(Roll)、纵摇(Pitch)和首摇(Yaw)。

图8 平台六自由度运动

3 环境条件

为全面研究所提出的3×3阵列Spar平台漂浮式风电场平台的动态响应特性，本文考虑普通海况和恶劣海况两种运行环境，具体环境参数设定如表5所示，风为稳态风，波浪为不规则波，基于P-M谱生成，风波入射一致，均为风力机风轮迎风面方向(最恶劣海况)。为保证时域统计值(最大值、标准差)满足统计规律，时域统计值均基于多组波浪种子结果的平均值，波浪种子数包括1、500、1 000、2 000、5 000、10 000。

表5 环境载荷参数

4 结果与分析

4.1 计算结果可靠性验证

为验证计算结果准确性，将单个漂浮式风力机Spar平台频域计算结果与韩国海洋研究与开发协会(Korean Ocean Research and Development Institute，KORDI)于2012年通过水池试验获得的试验值[34]进行对比。KORDI所做试验考虑迎浪条件下漂浮式风力机Spar平台的运动响应，波浪为规则波，频率范围为0.1～1.5 rad/s。漂浮式风力机Spar平台纵荡、垂荡及纵摇RAO随波浪频率的变化及与试验值的对比情况如图9所示。

由图9可知，垂荡RAO模拟值与试验值吻合度较高，纵荡、纵摇自由度虽有轻微的差别，但考虑到试验误差等因素，本文模拟结果与试验值的吻合度可视为高度一致。因此，验证了本文水动力建模及计算结果的准确可信，并进一步验证了前文网格划分的准确性与可靠性。

图9 频域RAO及与试验值对比

4.2 原始漂浮式风电场Spar平台首摇、横摇响应

传统海工领域，研究对象大都基于单浮体，系泊系统的布置一般具有对称特征或中心对称特征，研究环境条件一般为风波同向入射的最恶劣环境条件，因此，分析浮体运动时一般仅分析纵荡、垂荡以及纵摇响应。但对于本文所提出的多平台阵列漂浮式风电场，位于两侧的平台在外界载荷(风浪)激励下运动时，平台两侧的系泊沿y向产生的水平分力无法时刻保证大小相等、方向相反，由此产生了上文所分析的横荡运动；不仅如此，平台两侧系泊沿y向所产生的竖向分力亦无法时刻保证大小相等，二者产生的力矩若无法及时抵消，伴随而来的将是平台横摇运动的产生，因此，对3×3阵列Spar平台漂浮式风电场，平台的横摇运动是格外需要重视的运动特征参数。此外，当平台产生纵荡运动时，平台的纵荡回复力/力矩除去平台两侧的系泊所提供的部分，平台上下两侧系泊所提供的回复力在x方向的水平分量亦提供了部分纵荡回复力/力矩，上部为固定悬链线，底部为链接悬链线，因此，上下所产生的纵荡回复力亦无法保证时刻大小相等、所引发的扭转力矩亦无法时刻抵消，由此平台将产生首摇运动。因此，对3×3阵列Spar平台漂浮式风电场，各平台首摇运动是另一不容忽视的运动特征参数。

不考虑风载荷，仅考虑波浪单独作用时，两种环境条件下3×3阵列Spar平台漂浮式风电场平台的横摇、首摇运动时历曲线分别如图10、图11所示。由图10、图11可知，两种环境条件下，随着波浪作用时间的增加，基于Spar平台的漂浮式风电场中各平台的首摇、横摇运动逐渐加剧，普通海况下，平台的横摇运动幅度约25°，首摇运动幅度约30°，恶劣海况下，平台的横摇运动幅度约60°，首摇运动幅度达500°，说明平台发生了极大的扭转运动。这对于漂浮式风电场的安全运行是非常不利的，更说明系泊系统直接与Spar平台主体链接建立漂浮式风电场的方法不可行。此外，由图10可知，普通海况下，平台P1、P4、P7横摇、首摇首次出现不稳定约在20 000 s时，因此对于共用系泊系统多平台阵列漂浮式风电场平台动态响应的研究，建议仿真时间增加至5 h。

图10 普通海况下3×3阵列Spar平台漂浮式风电场平台横摇、首摇响应

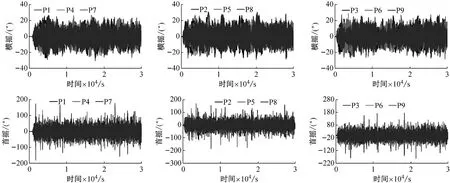
图11 恶劣海况下3×3阵列Spar平台漂浮式风电场平台横摇、首摇响应

4.3 两种提高漂浮式风电场Spar平台稳定性的方法

Spar平台主体直径仅9.4 m，较之半潜式平台、Barge平台，Spar平台首摇回转半径较小，首摇转动惯量因而相对更小(回转半径的平方倍)，当所受到的首摇力矩不平衡时容易发生首摇运动。漂浮式风力机Spar平台六自由度之间具有耦合效应，极大的首摇响应将导致极大的横摇响应。事实上，考虑系泊回复力时，外界载荷激励下漂浮式风力机Spar平台的运动，本质上可视为一个具有质量、刚度及阻尼的刚体系统六自由度的动力学求解问题。因此，为了抑制平台的首摇响应，可通过三种方式：① 增大平台的首摇附加质量；② 增大平台的首摇阻尼；③ 增大平台的首摇回复力矩。

与漂浮式风力机Spar平台垂荡响应具有垂荡方向往复性的特点相同，所提出的Spar平台漂浮式风电场中的各平台的首摇响应虽波动幅度较大，但仍保持往复周期性。为此，针对前文第一种和第二种方式，借鉴前文垂荡板可有效抑制漂浮式风力机Spar平台垂荡响应、进而提高垂荡稳定性的研究经验，本文提出了应用于Spar平台漂浮式风电场的首摇响应抑制装置“首摇阻尼板”，即在Spar平台主体布置一系列竖直安装的薄板，安装首摇阻尼板的Spar平台漂浮式风力机如图12所示。与垂荡板类似，首摇阻尼板可以增大平台的首摇附加质量与首摇阻尼，进而达到抑制平台首摇响应的效果。

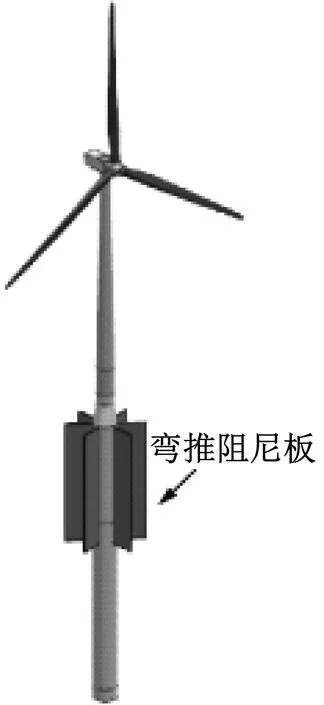
图12 安装首摇阻尼板的Spar平台漂浮式风力机

安装首摇阻尼板前后，Spar平台首摇阻尼板的首摇附加质量幅频特性曲线如图13所示。由图13可知，原始单个Spar平台首摇附加质量几乎为0，安装首摇阻尼板后平台首摇附加质量增大至7×109 kg·m2，约为原始单个Spar平台首摇转动惯量(2×108 kg·m2)的35倍。

图13 首摇附加质量幅频特性曲线

针对第三种方式，Spar平台系泊系统首摇回复力矩基数相对较小，轻微的扰动对系泊回复力矩可能产生较大的影响，尤其是恶劣海况下。因此，为了减小恶劣海况下扰动对首摇回复力矩相对较大的不利影响，本文提出了适用于增强Spar平台漂浮式风电场平台首摇稳定性的方法——增大系泊系统作用半径，即“系泊系统链接点外移”的方法，如图14所示。当系泊系统链接点外移时，系泊系统首摇回复力矩作用半径增大，此时系泊系统首摇回复力矩基数成倍提升，当平台两侧的系泊系统产生的首摇回复力矩不一致时，对平台的合首摇回复力矩的影响将减弱，即扰动对合首摇回复力矩影响的相对值极大幅度减小，由此达到增大Spar平台漂浮式风电场平台首摇稳定性的目的。

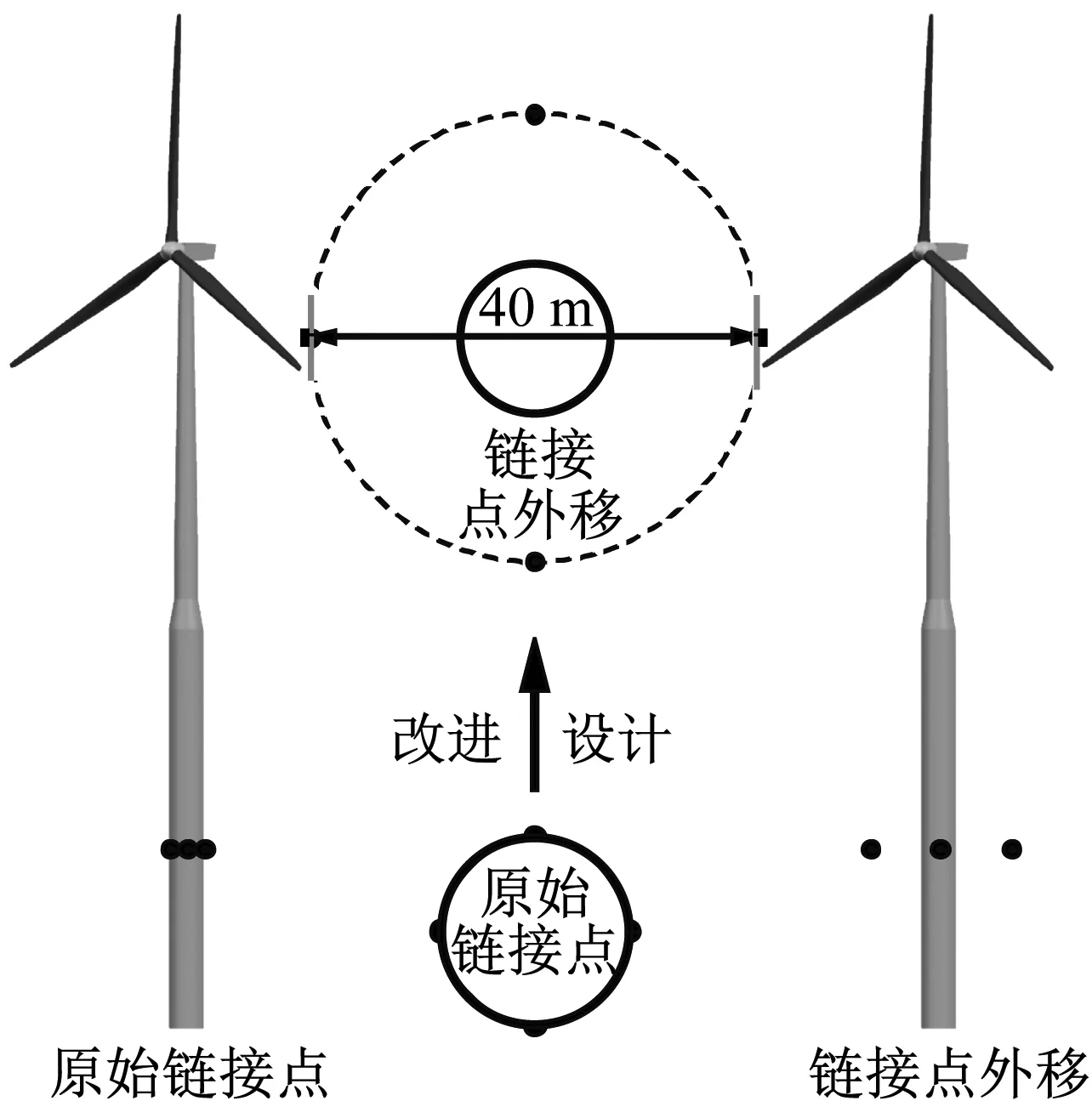
图14 系泊系统链接点外移示意图

4.4 首摇阻尼板对漂浮式风电场Spar平台横摇、首摇响应影响

为研究所提出的首摇阻尼板对3×3阵列Spar平台漂浮式风电场平台的横摇、首摇响应的影响，建立安装首摇阻尼板的Spar平台漂浮式风力机整机模型。进一步采用链接悬链线将安装首摇阻尼板的Spar平台进行链接，建立了3×3阵列Spar平台漂浮式风电场。两种环境条件下，安装首摇阻尼板Spar平台漂浮式风电场平台的横摇、首摇运动时历曲线分别如图15及图16所示。

由图15可知，普通海况下，安装首摇阻尼板后，以风波入射方向为参考(x轴负方向)，① 位于中心处(x轴)的平台P1、P4、P7横摇、首摇角度始终为0；② 位于上下两侧的平台P2、P3、P5、P6、P8、P9首摇、横摇波动幅度均不超过0.1°，即几乎不存在横摇、首摇运动。由此可见，普通海况下安装首摇阻尼板能够明显抑制Spar平台漂浮式风电场的横摇、首摇响应，因此，普通海况下，所提出的首摇阻尼板能够极大的提高Spar平台漂浮式风电场的横摇、首摇稳定性，其有效性得到验证。

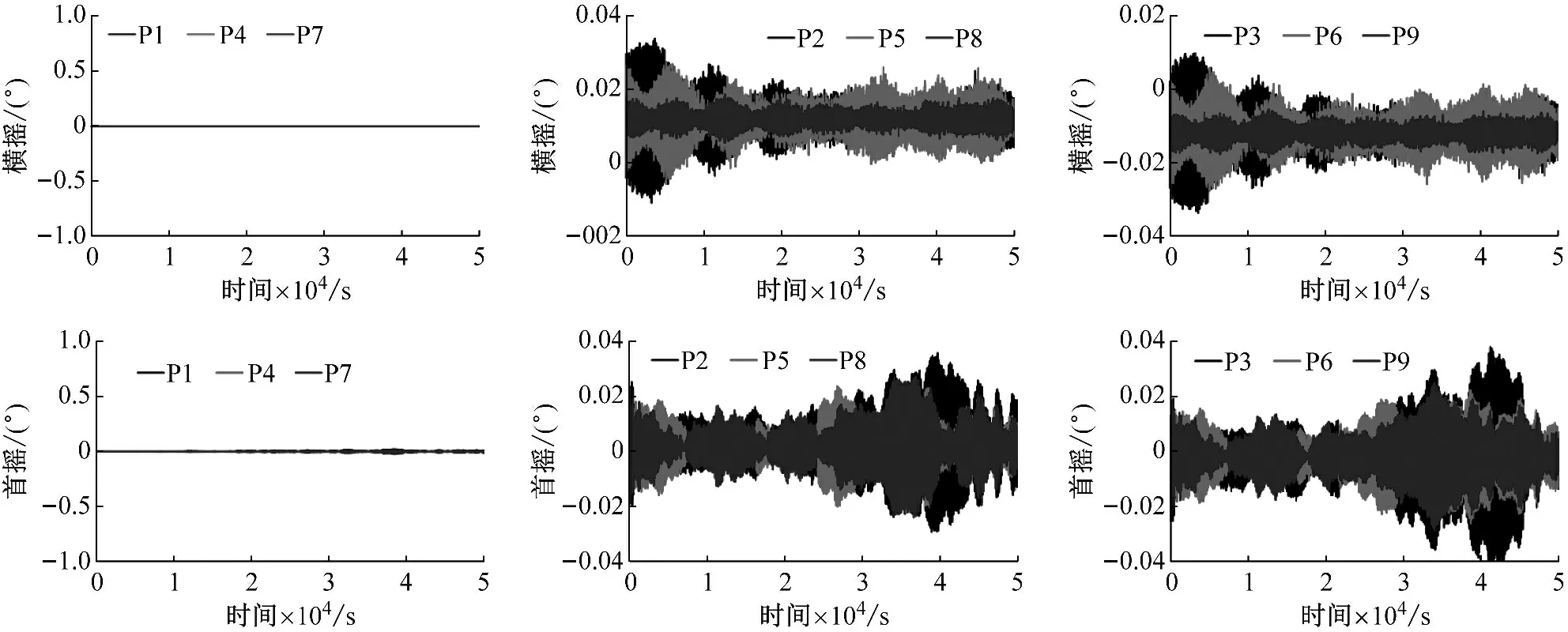
图15 普通海况下首摇阻尼板对3×3阵列Spar平台漂浮式风电场平台横摇、首摇响应影响

由图16可知，恶劣海况下，安装首摇阻尼板后，① Spar平台漂浮式风电场中的各平台在相当长的时间内，其横摇、首摇波动幅度几乎为0，稳定性较好；② 随着时间的推移，平台逐渐产生轻微的横摇、首摇运动，随后横摇、首摇响应急剧变大，最终达到波动的平衡，横摇响应波动幅度均约为30°，首摇响应波动幅度均约为120°。由此可见，恶劣海况下，安装首摇阻尼板的Spar平台漂浮式风电场仍具有极大的横摇、首摇响应。

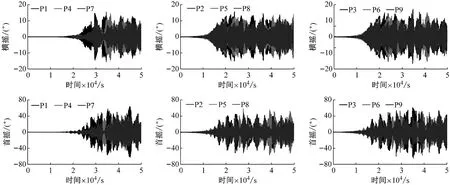
图16 恶劣海况下首摇阻尼板对3×3阵列Spar平台漂浮式风电场平台横摇、首摇响应影响

4.5 系泊链接点外移对漂浮式风电场Spar平台横摇、首摇响应影响

系泊链接点外移时，3×3阵列Spar平台漂浮式风电场示意图，如图17所示。

图17 系泊链接点外移后Spar平台漂浮式风电场

两种环境条件下，考虑风波耦合作用，系泊链接点外移时，Spar平台漂浮式风电场的横摇、首摇响应时历曲线分别如图18、图19所示。

由图18可知，普通海况下，① 以风波入射方向(-180°，即x轴负方向)为参考，位于中心线处的平台P1、P4、P7首摇、横摇始终为0°；② 位于上侧的平台P2、P5、P8与下侧的平台P3、P6、P9横摇、首摇响应时历曲线关于x轴对称，由此可见，上下两侧的平台的运动具有完全对称的特点；③ 上下两侧的平台的首摇波动幅度均不超过1°，横摇波动幅度均不超过0.1°。由此可见，普通海况下，系泊链接点外移能够极大的降低Spar平台漂浮式风电场的首摇、横摇响应，平台首摇、横摇稳定性得到了极大的提高。

图18 普通海况下系泊链接点外移对3×3阵列Spar平台漂浮式风电场平台横摇、首摇响应影响

由图19可知，恶劣海况下，① 与普通海况相同，以风波入射方向(-180°，即x轴负方向)为参考，位于中心线处的平台P1、P4、P7首摇、横摇始终为0°；② 与普通海况下响应相同，位于上侧的平台P2、P5、P8与下侧的平台P3、P6、P9横摇、首摇响应时历曲线关于x轴对称，由此可见，上下两侧的平台的运动具有完全对称的特点；③ 上下两侧的平台首摇波动幅度约2°，横摇波动幅度约0.5°，由此可见，恶劣海况下，系泊链接点外移能够极大的降低Spar平台漂浮式风电场的首摇、横摇响应，平台首摇、横摇稳定性亦能够得到极大的提高。

图19 恶劣海况下系泊链接点外移对3×3阵列Spar平台漂浮式风电场平台横摇、首摇响应影响

综上，普通海况、恶劣海况两种环境条件下，系泊链接点外移均能够极大的提高Spar平台漂浮式风电场平台的首摇、横摇稳定性。因此，下文将重点研究系泊链接点外移对3×3阵列Spar平台漂浮式风电场平台动态响应的影响。

4.6 普通海况下系泊链接点外移对漂浮式风电场Spar平台动态响应影响

普通海况下，系泊链接点外移时，3×3阵列Spar平台漂浮式风电场平台在xOy平面内的运动轨迹图，如图20所示，平台纵荡响应时频特性曲线如图21所示。由前文分析已知，普通海况下上侧平台与下侧平台动态响应(横摇、首摇响应)具有对称性的特点，故此处仅给出位于中心线处(以风波入射方向为参考，即x轴负方向)平台P1、P4、P7和上侧平台P2、P5、P8的运动轨迹图、纵荡响应时频特性曲线。

由图20、图21可知，普通海况下，所提出的3×3阵列Spar平台漂浮式风电场平台运动轨迹，① 位于中线处的平台P1、P4、P7不存在横荡运动，位于两侧的平台存在一定的横荡运动；② 横荡运动波动幅度，第一列平台约为0.6 m，第二列平台约为1 m，第三列平台约为3 m，由此可见，随着与左侧固定悬链线距离的增加，平台横荡运动波动幅度逐渐增加；③ 纵荡位移最大值(沿x轴负方向)，第一列平台约为22.5 m，第二列平台约为47 m，第三列平台约为50 m，由此可见，随着与左侧固定悬链线距离的增加，平台纵荡位移最大值(沿x轴负方向)逐渐增加，这主要是由于平台初始阶段的低频平均漂移，导致后列平台产生了相对于前列平台的运动；④ 位于中心线处的平台的平均漂移位置、纵荡响应最大值(沿x轴负方向)均大于位于两侧的平台，这主要是因为位于上、下两侧的平台的纵荡回复力除去左侧固定悬链线提供的部分，还由上下两侧的固定悬链线提供，上下两侧固定悬链线的纵荡回复力传递到中线处平台需经过外侧的平台，中线处平台会产生相对于外侧平台的纵荡运动；⑤ 由纵荡响应频域特性曲线可知，普通海况下，平台响应以低频响应为主，波频响应其次，且随着平台与左侧悬链线距离的增加，平台低频响应峰值越大，这侧面反映了纵荡漂移最大位置的大小(沿x轴负方向)，且与前面分析相吻合。

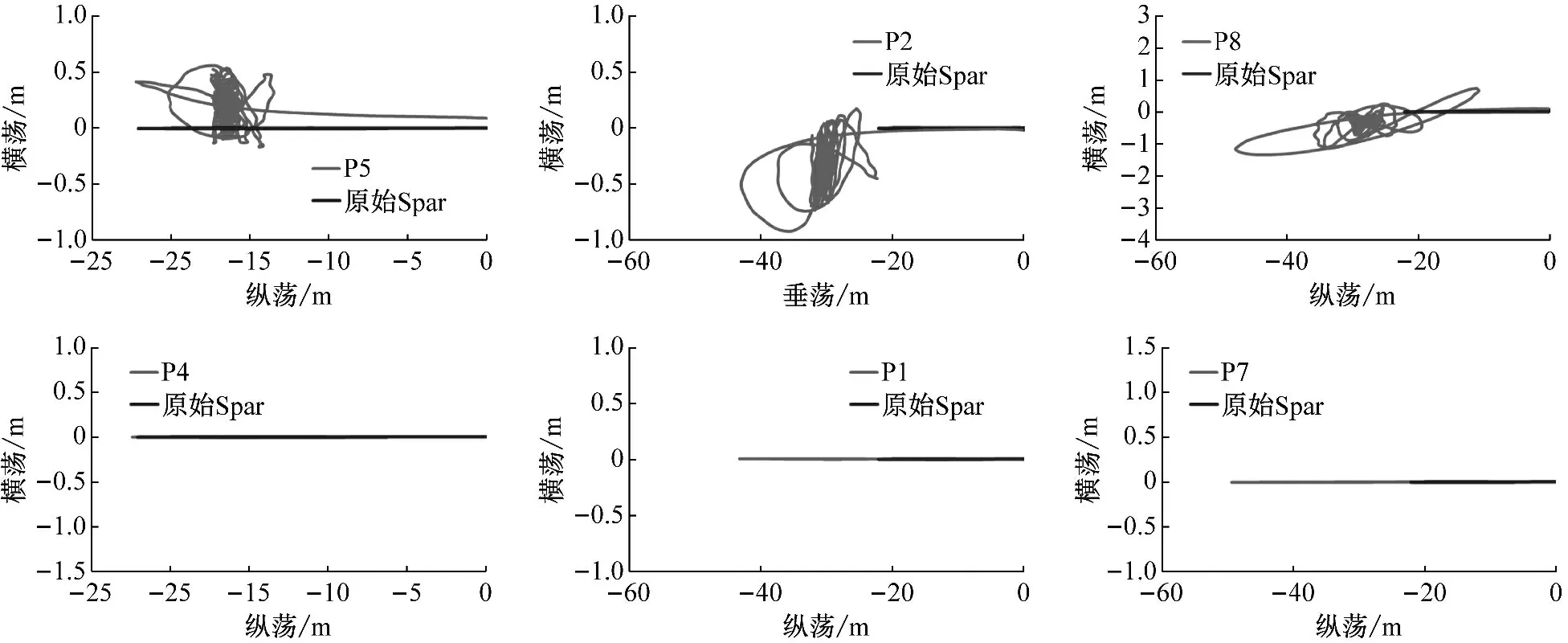
图20 普通海况下3×3阵列Spar平台漂浮式风电场平台运动轨迹

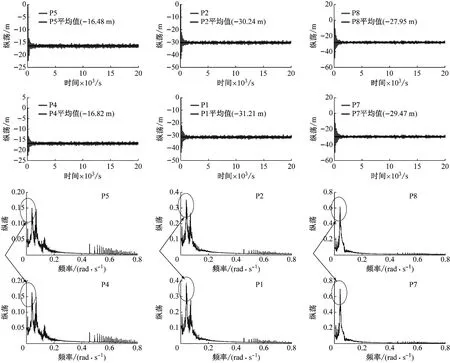
图21 普通海况下3×3阵列Spar平台漂浮式风电场平台纵荡响应时频特性曲线

普通海况下，原始单个Spar平台和3×3阵列Spar平台漂浮式风电场平台时域垂荡、纵摇响应及机舱加速度统计值，如图22所示，以下统计值均基于多组不同波浪种子数计算结果平均值。

图22 普通海况下3×3阵列Spar平台漂浮式风电场平台垂荡、纵摇及机舱加速度统计值

由图22可知，普通海况下，① 对于垂荡响应，位于第一列平台P4、P5、P6垂荡响应波动幅度稍大于原始单个Spar平台，但其垂荡响应标准差和原始单个Spar平台差别较小，说明P1、P2、P3平台的垂荡响应仅仅是增大了某些个时刻的响应幅值，但其垂荡稳定性仍与原始单个Spar相当，位于第二列的平台P1、P2、P3垂荡波动幅度、垂荡响应标准差均远小于原始单个Spar平台，说明第二列平台的垂荡稳定性得到了很大的提高，位于第三列的平台P7、P8、P9垂荡波动幅度、垂荡响应标准差均稍小于原始单个Spar平台，说明第三列平台的垂荡稳定性得到了一定的提高，由此可见，普通海况下，系泊链接点外移能够较大程度的提高Spar平台漂浮式风电场的垂荡稳定性；② 对于纵摇响应，Spar平台漂浮式风电场所有平台的纵摇波动幅度、纵摇响应标准差均小于原始单个Spar平台，说明所有平台的纵摇稳定性得到了极大的提高，由此可见，普通海况下，系泊链接点外移能够极大的提高Spar平台漂浮式风电场的纵摇稳定性；③ 对于机舱加速度，位于第二、第三列平台的机舱加速度波动幅度虽然大于原始单个Spar平台，但其标准差小于原始单个Spar平台，说明仅仅是增大了某些时刻点的机舱振动加速度，但整体的机舱振动稳定性得到了提高，此外，位于第一列平台的机舱加速度波动幅度、标准差均小于原始单个Spar平台。总体而言，普通海况下，系泊链接点外移提高了Spar漂浮式风电场机舱的振动稳定性。

由此可见，普通海况下，系泊链接点外移时，Spar平台漂浮式风电场平台的垂荡、纵摇及机舱振动稳定性均得到了不同的程度的提高。

4.7 恶劣海况下系泊链接点外移对漂浮式风电场Spar平台动态响应影响

普通海况下，系泊链接点外移时，3×3阵列Spar平台漂浮式风电场平台在xOy平面内的运动轨迹图，如图23所示，平台纵荡响应如图24所示。

由图23、图24可知，恶劣海况下3×3阵列Spar平台漂浮式风电场平台运动轨迹特点类似，具有以下特点：① 位于中线处平台P1、P4、P7不存在横荡运动，位于两侧的平台有一定程度的横荡运动；② 恶劣海况时，沿x轴负方向(即风波入射方向)，平台纵荡响应最大值、纵荡波动平衡位置，恶劣海况均小于普通海况，较之于普通海况，恶劣海况下平台产生了沿x轴正方向的纵荡运动，这主要是由于恶劣海况下，平台的纵荡响应以波频响应为主，低频响应其次，低频响应主要由风载荷引起，恶劣海况下风载荷小于普通海况，因此沿x轴负方向平台纵荡响应最大值、纵荡波动平均位置均减小，之所以平台产生了沿x轴正向的运动，这主要是由恶劣海况下的波频运动导致，波频运动由波浪载荷引起，恶劣海况下平台的波频运动急剧增大，有可能超过风载荷引起的低频漂移平均位置，上述二者的叠加导致了平台沿x轴正向的纵荡响应；③ 位于中线处(x轴)平台P1、P4、P7纵荡最大位置、波动平均平衡位置均稍大于位于两侧的平台P2、P5、P8，这主要是由于位于中线处的平台产生了相对两侧平台的运动。

图23 恶劣海况下3×3阵列Spar平台漂浮式风电场平台运动轨迹

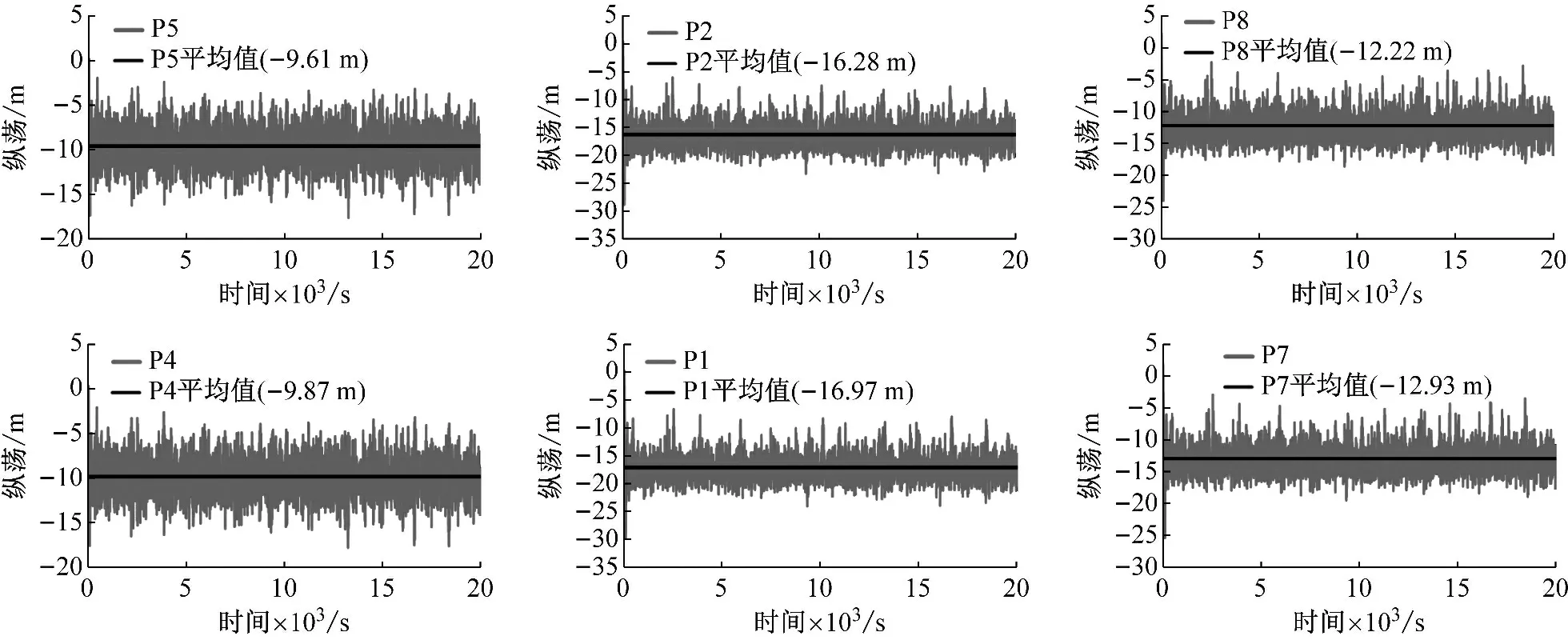
图24 恶劣海况下3×3阵列Spar平台漂浮式风电场平台纵荡响应

系泊链接点外移时，恶劣海况下，原始单个Spar平台和3×3阵列Spar平台漂浮式风电场平台时域垂荡、纵摇响应及机舱加速度统计值，如图25所示，统计值均基于多组不同波浪种子数计算结果的平均值。

由图25可知，恶劣海况下，系泊链接点外移时，① 对于垂荡响应，Spar平台漂浮式风电场平台垂荡波动幅度、垂荡响应标准差均小于原始单个Spar平台，且位于第一列的平台P4、P5、P6垂荡波动幅度、垂荡响应标准差减小幅度非常明显，由此可见，系泊链接点外移时，恶劣海况下Spar平台漂浮式风电场平台的垂荡稳定性得到了极大的提高；② 对于纵摇响应，Spar平台漂浮式风电场平台纵摇波动幅度、纵摇响应标准差均小于原始单个Spar，由此可见，系泊链接点外移时，恶劣海况下Spar平台漂浮式风电场平台的纵摇稳定性得到了极大的提高；③ 对于机舱加速度，第一列平台P4、P5、P6波动幅度大于原始单个Spar平台，第三列平台P7、P8、P9稍大于原始单个Spar平台，但上述两列平台机舱加速度标准差小于原始单个Spar平台，说明上述平台增大的仅仅是个别时刻的响应幅度，但机舱整体的振动稳定性得到了提高，第二列平台P1、P2、P3的机舱加速度波动幅度、响应标准差均小于原始单个Spar平台，由此可见，系泊链接点外移时，Spar平台漂浮式风电场机舱振动稳定性得到提高。