大直径桩扭转波法测试的数值分析
2021-02-05程晓东洪天求卢志堂刘东甲
程晓东, 洪天求, 卢志堂, 高 放, 刘东甲
(合肥工业大学 资源与环境工程学院,安徽 合肥 230009)
目前,对于基桩的完整性检测,以低应变反射法应用最为广泛。但现行的低应变动测法仅利用纵波进行测试存在不足。通过文献[1]的研究结果可知,纵波检测在桩身浅部存在测试盲区,无法对桩身浅部的完整性做出判断。随着基桩动测技术的发展与进步,众多学者也对原有单一的纵波动力测桩理论进行了研究。文献[2]通过对自由杆中扭转波的特性分析,发现扭转波易于识别浅部缺陷,并提出了简便实用的测试方法,大大地提高了扭转波应用于低应变动力测桩的可操作性;文献[3]利用数值方法研究了非完整桩的扭转振动,得到了各种典型缺陷桩的理论曲线;文献[4]建立了三维轴对称黏弹性土体中基桩扭转的振动模型,并分析了基桩扭转振动的动力特性;文献[5]通过积分方程的方法研究了均匀弹性地基中单桩的扭转振动特性。上述研究很好地阐述了扭转波应用于低应变测试的可行性,极大地丰富了动力测桩的理论。其后的研究中,文献[6]研究了轴对称条件下端承桩在横观各向同性土体中的耦合扭转振动响应问题;文献[7]把桩看作一维杆,将土体视作三维轴对称黏弹性介质,对黏弹性地基中现浇混凝土大直径管桩(简称PCC桩)扭转振动频域特性进行了理论研究;文献[8]对饱和土中管桩扭转振动进行了理论分析。
虽然目前对基桩扭转研究的工作已经较多,但大多将桩看作一维杆处理,这种近似对小直径桩是合理的,但对大直径桩(直径大于0.8 m),这种近似处理与实际存在一定的偏差。文献[9]曾分析了尺寸效应对于低应变测试的影响,发现当桩身直径较大时,一维假定不再成立。为此,本文采用三维波动理论,建立了空间轴对称条件下大直径桩的瞬态扭转振动模型;采用交错网格有限差分法求得三维条件下大直径桩的桩顶环向速度响应,探讨了扭转波测试的影响因素,并给出了桩身截面变化对测试结果的影响;最后结合实测案例分析,验证数值模拟方法的可靠性,展示了扭转波测试的前景。
1 计算模型及定解问题
计算模型如图1所示,在柱坐标中,半径为R、长为L的基桩嵌入在半无限土中。桩顶受到轴对称的瞬态扭矩m作用。假定桩和土均为各向同性且均匀连续的弹性介质,桩土界面不分离。桩、桩周土和桩底土的密度及剪切模量分别为ρp、μp、ρs、μs和ρb、μb。
由于实际模型区域是无穷大的,考虑波在桩中传播一个回程这段时间内,边界上的反射波尚未到达桩身就能满足预期要求,据此可以截取桩身之外一定范围的区域作为人工边界。图1中给出了边界范围,对应的桩周土径向厚度分别为rb,桩底土厚度为zb。

图1 计算模型
当桩顶受到轴对称的瞬态环向扭矩作用时,桩-土系统中的应力和速度也是轴对称分布的,由弹性理论得出柱坐标下由速度与应力表达的运动方程如下:
(1)
其中:ρ为材料质量密度;vθ为质点振动的环向速度;σrθ、σzθ为剪应力;μ为剪切模量。
初始条件:由于桩土系统在瞬态扭矩作用前处于静止状态,因此在初始时刻,桩土系统的速度及应力均为0。
边界条件:考虑到在桩顶施加纯扭矩比较困难,因此本文在桩侧施加切向力,以等效代替环向扭矩作用,则对应的边界条件可表示为:
(2)
其中,t0为脉冲宽度。
衔接条件:小应变情况下,桩-土界面以及土层界面不分离,此处应力与速度连续。
由(1)式及上述初边值条件及衔接条件便构成了桩-土系统扭转振动的定解问题。
2 数值算法
2.1 差分方程
为实现轴对称条件下(1)式的求解,这里引入常用于桩基振动分析的交错网格有限差分法[10-12],其中网格划分如图2所示。从图2可以看出,质点振动的环向速度vθ、剪应力σrθ和σzθ在网格上交错布置,其中材料参数(ρ,μ)的采样位置与vθ的采样位置一致。
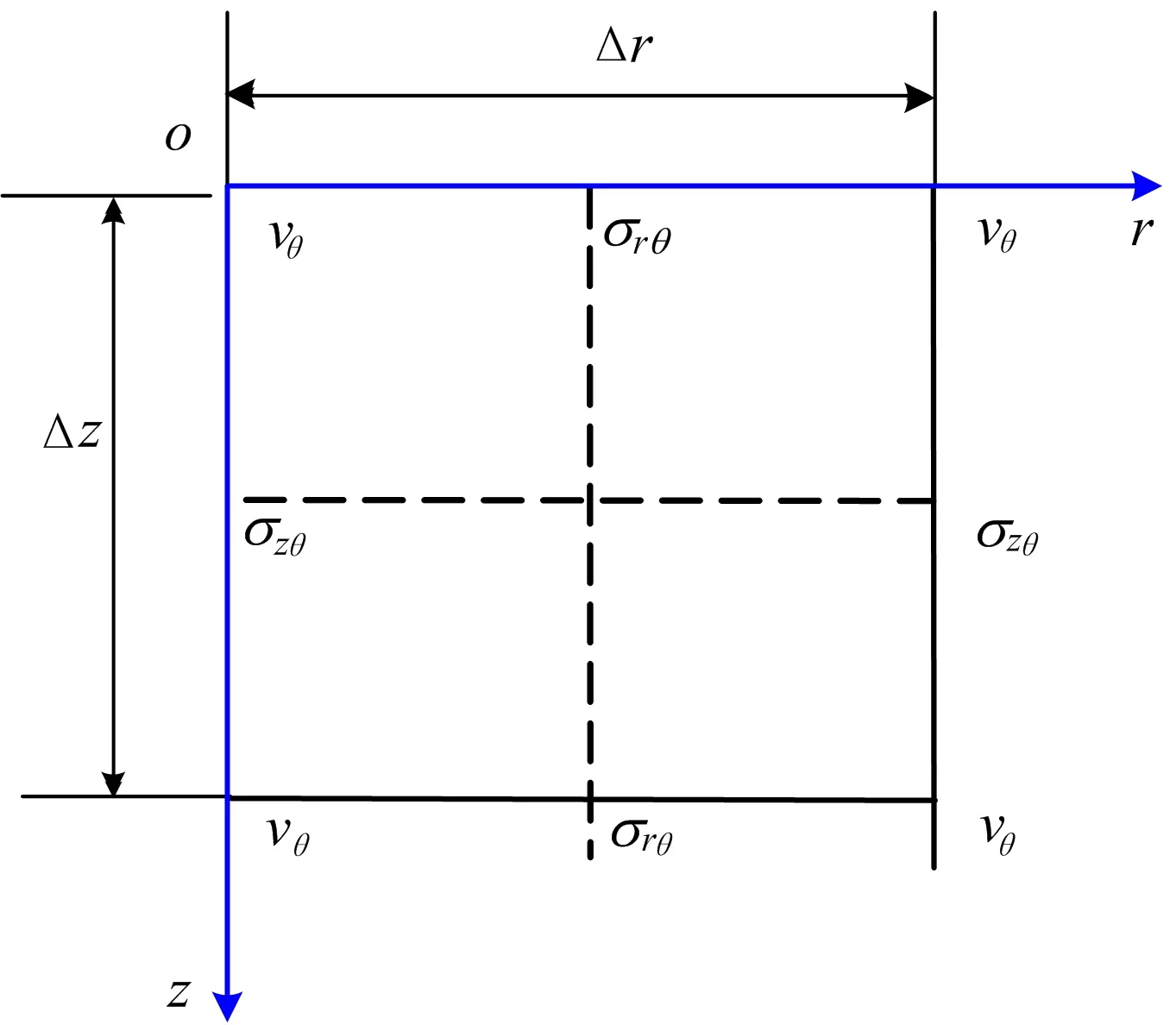
图2 交错网格布置
对于桩-土界面单元的材料参数,需要通过如下等效方法进行:
(3)
其中,ρb、μf和ρb、μf分别为计算点前后相邻2个采样点的质量密度及剪切模量。通过调整对桩-土界面处的材料参数值,就可以保证速度和应力连续,且差分格式保持不变。
为使差分方程表达形式简洁明了,(4)式为下文中使用的算子,即
(4)
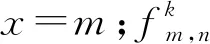
根据网格划分规则和时域有限差分,可将(1)式写成如下具有二阶精度的差分方程组:
(5)
(6)
(7)
为保证差分方程的解是稳定收敛的,必须满足Courant稳定性条件[13],即
(8)
其中,Cmax为波在桩中传播的最大波速。
对于桩顶,采用剪应力连续条件的差分格式可以得到更好的结果。由(1)式中弹性波动方程可得:
(9)
2.2 计算流程

(3) 依次增大时间步k,重复步骤(1)、步骤(2)。初始时刻,应力与速度分量均为0。按照以上步骤编写程序,就可以实现数值求解。
3 计算结果及参数分析
3.1 算例展示
本文根据上述算法和计算流程,编制了Matlab计算程序,对大直径摩擦桩的瞬态扭转振动问题进行了正演计算。计算参数如下:桩身密度为2 400 kg/m3,桩长为7.0 m,桩身直径为0.8 m,剪切模量为14.4 GPa;桩周土及桩底土密度参数取值相同,密度及剪切模量分别为1 900 kg/m3和48.6 MPa。本文中的计算网格参数为Δr=1 cm,Δz=2 cm。设置土层径向厚度为4 m,桩底土厚度为4 m,可以避免边界反射波的影响。激振扭矩脉冲宽度t0=1.0 ms。
桩顶不同径向位置的环向速度响应如图3所示。因为本文只关注波形变化,所以环向速度均经过无量纲化处理。虽然激振扭矩施加在桩顶边缘(r=R处),但从图3a可以看出,越靠近桩顶中心,入射波振幅反而越大,对应的桩底反射波振幅也越大。因为入射波从桩侧向内传播过程中不断汇聚叠加,所以在桩顶中心区域的入射波振幅比外侧更大。此外还可以看出,桩底反射波与入射波同向。为进一步分析不同位置速度响应的差异,将速度进行归一化(即令入射波幅值均为1),得到速度波形(图3b)。从图3b可以看出,归一化后,不同径向位置的桩底反射波振幅也基本相同。入射波和桩底反射波之间的高频振荡,即三维干扰(图3c),会对桩基完整性评价造成干扰,而一维理论无法反映这一现象。从图3b和图3c可以看出,当r=0.8R时,环向速度波形中三维干扰最弱。另外,入射波峰值到时不同,但桩底反射波到时基本一致。

图3 桩顶不同径向位置环向速度响应
扭转波传播速度CT也是需要关注的参数之一,根据峰-峰值时间差ΔT及桩长L,可以由下式计算出波速,即
CT=2L/ΔT
(10)
扭转波波速见表1所列。从表1中可以看出,径向位置不同,得到的扭转波波速也不一致,这是由于入射波从激振点沿径向传至采样点产生滞后时差,也是一维理论不能反映的现象之一。根据一维理论可知,两者计算公式分别为:
(11)
(12)
其中,Ep表示弹性模量。由(11)式、(12)式可知一维扭转波波速C1T=2 449 m/s,一维纵波波速C1P=3 794 m/s。表1所求得的三维扭转波波速与一维扭转波波速较为接近,且明显小于纵波波速。
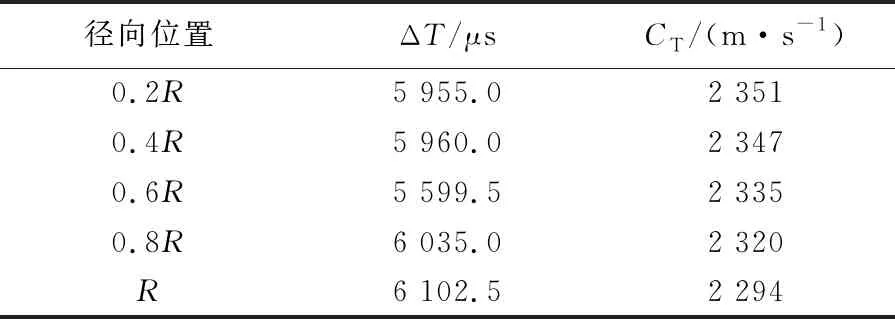
表1 扭转波波速
3.2 脉冲宽度影响
脉冲宽度t0分别为2.0、0.5 ms时的速度响应曲线如图4所示。
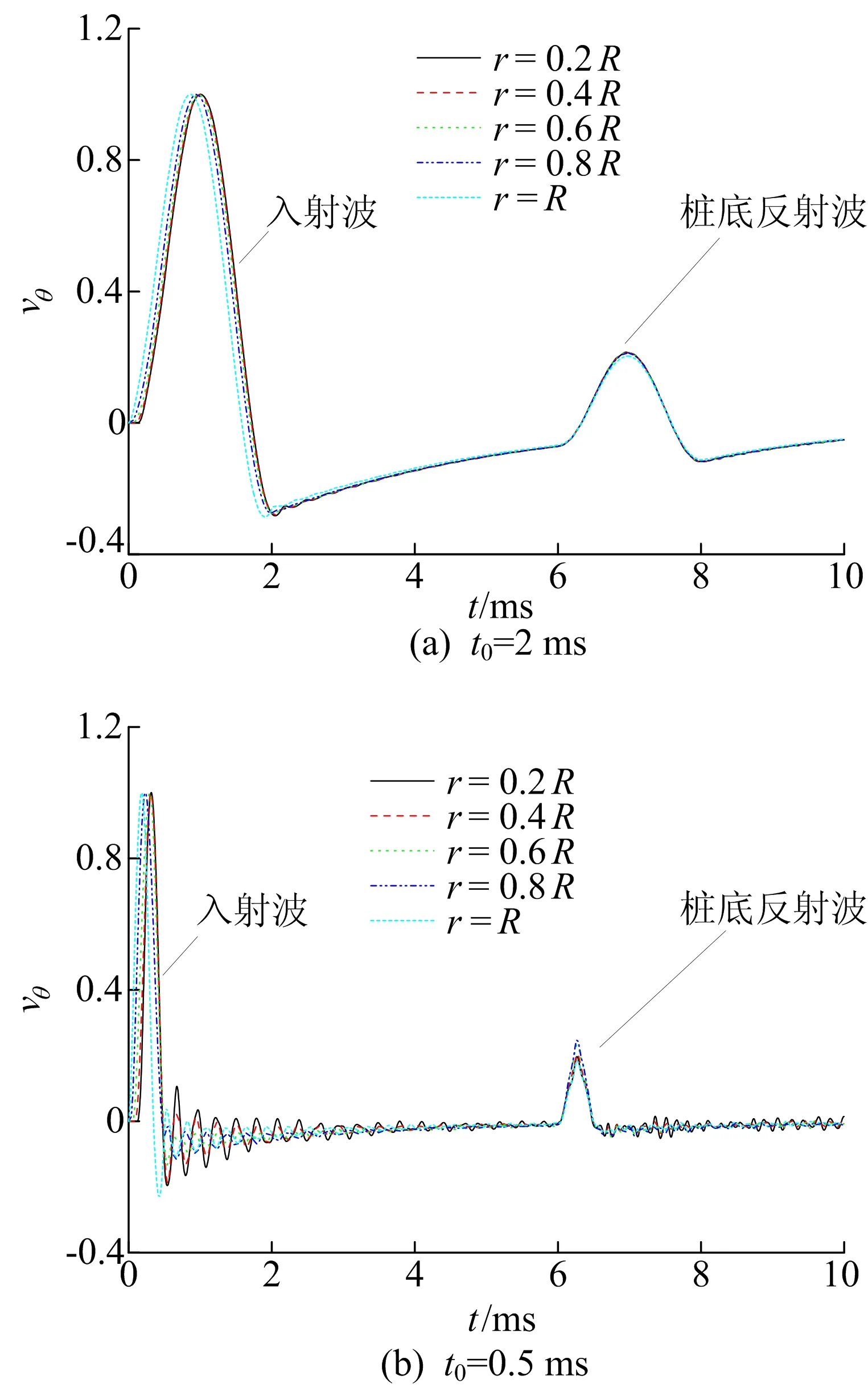
图4 脉冲宽度对桩顶速度响应的影响
图4中曲线均经过归一化处理。将图4与图3进行对比可以看出,随着脉冲宽度增大,三维干扰逐渐变弱。当脉冲宽度为2 ms时,三维干扰已经不明显,各个径向位置的速度曲线波形基本相同。从图4b可以看出,r=0.8R处的三维干扰仍然最弱。
3.3 截面变化时桩顶速度响应
由3.1节和3.2节可知,桩顶r=0.8R处三维干扰比其他位置弱,因此选取该位置作为采样点。缩径桩、扩径桩、完整桩的桩顶速度响应如图5所示,图5中脉冲宽度t0=1.0 ms。扩径段直径为1.2 m,缩径段直径为0.8 m,两者均位于2.0~2.5 m处。从图5可以看出,缩径处产生的反射波与入射波同向,扩径处产生的反射波与入射波反向,这与纵向敲击条件下桩顶的竖向速度响应规律一致。这表明,扭转波可为传统纵波法测桩提供有效补充或参考,尤其是桩顶不适合竖向敲击时。
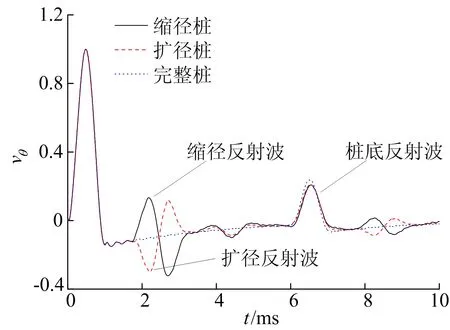
图5 截面变化时桩顶速度响应
3.4 案例分析
本节将根据实际测试案例来分析扭转波用于判别大直径的完整性的效果。实际测试时,很难在桩顶激发出纯扭转波,本文参考文献[2]提出的方法进行侧向敲击,激振与拾振方式如图6所示。
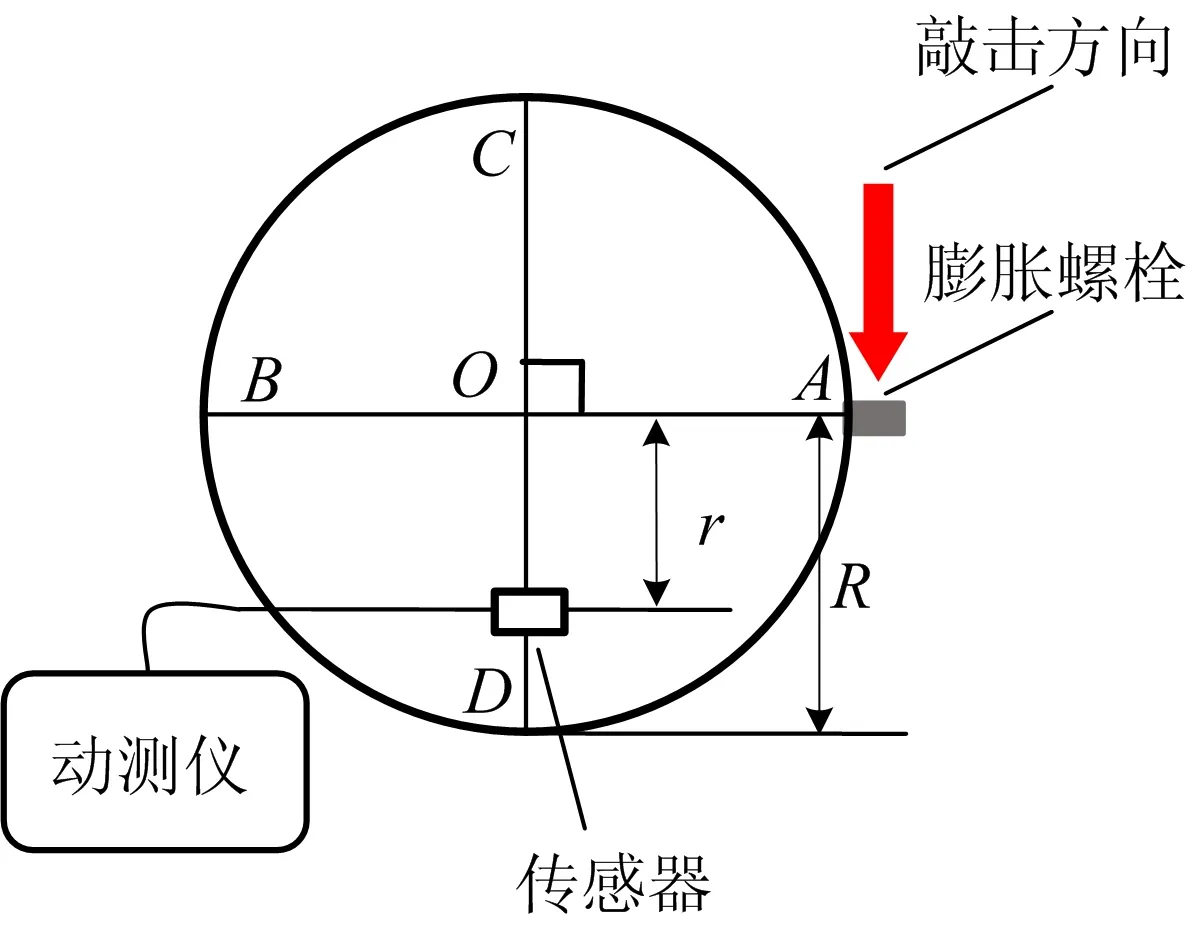
图6 激振与拾振布置
图6中敲击点为膨胀螺栓。需要注意侧向敲击不但引起扭转振动,还会引起横向振动。这里将激振位置同桩心连线OA与传感器同桩心连线OD正交,可以有效避免横向振动的影响。
实验所用测试仪器为武汉岩海公司生产的基桩动测仪,型号为RS-1616K(S)。所测试基桩为人工挖孔桩,桩长为7 m,桩身横截面半径为0.40 m。在施工时,曾将其开挖至离桩顶3.1 m,除去护壁层。填土时,在距离桩顶2.1 ~ 3.1 m处用模板围护,使得该范围没有桩周土;然后回填使得地面距离桩顶面0.2 m,即第1层厚度;再根据实地测量,桩体出露地面的横截面半径约为0.36 m。该桩场地土层情况如下:上部为建筑垃圾及素填土,下部为黏性土,越靠下位置的黏土越硬实。根据该桩及所处场地的条件,将桩-土系统划分成5层,其相应各层参数取值见表2所列。注意模型中桩周第3层范围为木模,因此密度和剪切模量相对较低。另外,本次选择的传感器位置为0.8R处。
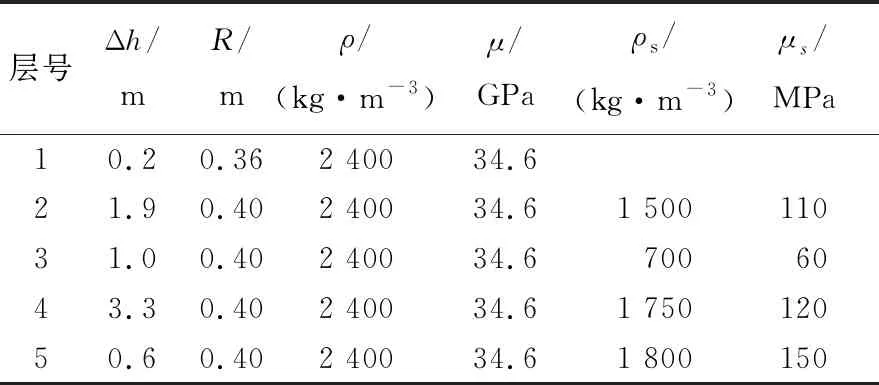
表2 桩土系统参数
实测结果与模拟结果对比如图7所示,从图7可以看出模拟结果与实测曲线吻合效果较好,这不仅证明了本文数值算法的合理性,而且也表明扭转波法测试具有良好的应用前景。
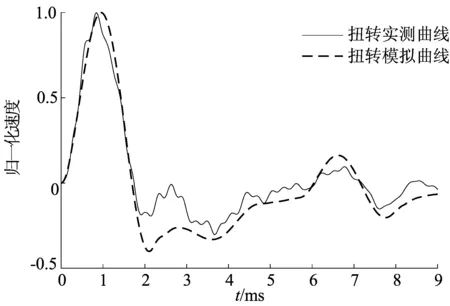
图7 实测曲线与模拟结果对比
4 结 论
本文将桩、土视为三维弹性体,建立了轴对称条件下基桩瞬态扭转的理论模型,利用交错网格有限差分法,并编制了相应的算法程序,实现了对该振动模型的求解,通过参数分析和实测案例对比,得到如下结论:
(1) 编制的交错网格差分法程序能够对大直径桩扭转振动进行数值分析,且实测曲线与计算曲线相吻合,表明该方法对桩基扭转波法检测问题具有很好的适用性。
(2) 桩顶不同位置的环向速度响应不同,越靠近外侧,入射波振幅和桩底反射波振幅越小。大直径桩桩顶扭转波测试结果面临三维干扰波影响,激振脉冲越窄,三维干扰越强烈。
(3) 与纵波法相一致,缩径处产生的反射波与入射波同向,而扩径处产生的反射波与入射波反向。扭转波法可为传统纵波法测桩提供有效补充或参照,建议检测时采用2种方法,以提高检测结果的准确性。
