信号交叉口左转非机动车交通冲突分析
2021-02-05周智文马健霄王冠森
周智文, 马健霄, 王冠森
(南京林业大学 汽车与交通工程学院,江苏 南京 210037)
长期以来,我国城市道路常有机动车与非机动车(简称“机非”)交通混合行驶的情况。城市道路一般使用隔离栏或标线以分离机非交通,因此交通冲突较少。而在交叉口,机非车流混行易导致交叉口频发交通事故,降低通行效率。在交叉口非机动车流中,对交叉口安全通行影响最明显的就是左转机非车辆间的相互干扰[1-2]。针对这种矛盾,目前主要有5种非机动车左转过街的组织方法:左转机非同时左转、左转非机动车二次过街、设置左转非机动车待转区、左转非机动车绿灯先亮及设置左转非机动车单独左转相位[3]。但各方法适用条件模糊,难以比较其优劣。
在交叉口非机动车交通特性方面,目前研究大多通过视频分析法得出各交通流相关参数,并研究各参数之间的相关性及其影响因素,提出假定模型,通过实际数据拟合求解参数,进行验证[4-6]。而求解模型关键在于确定模型影响因素和模型的形式,相关研究主要基于机非车辆的冲突机理分析各因素与机非冲突的关系[7-8],而已有研究一方面忽略了混合非机动车与机动车的冲突研究,另一方面缺乏定量分析具体流向的非机动车交叉冲突和膨胀冲突[9]。
目前,针对机非冲突下的通行效率主要有2种研究方法:① 基于实测的饱和流率折减系数法[10],该方法计算简单,但为了保证真实可靠,需大量实测数据;② 基于可接受穿越间隙理论,该方法适应性强,但计算复杂。对于多种非机动车左转组织方法的系统评价以及左转非机动车交通安全的相关研究较少。对于交叉口机非冲突的研究,大多仅考虑自行车流,缺乏对电动自行车的研究;冲突研究的重点偏向于机非冲突对交叉口通行效率或安全性的影响[11-12],缺乏综合考虑。针对交通冲突最为剧烈的左转非机动车,虽有多种改进组织方法,但大都缺乏合理的评价指标。
本文以左转非机动车与机动车的交叉冲突和膨胀冲突为研究对象,分析机非冲突对机动车通行能力的影响,并构建机非冲突数模型。
1 左转非机动车与机动车冲突分析
1.1 交叉口左转非机动车与机动车交叉冲突
目前,主要有2种方式分析信号控制交叉口的左转非机动车流线:方式1,采用和机动车相同的方式通过交叉口,如图1所示;方式2,采用和行人相同的方式通过交叉口,如图2所示。
对于左转非机动车与机动车交叉冲突点,选择最常见的四相位信号控制交叉口进行分析。四相位信号控制是指各进口道直行和左转信号相位分离、右转信号常绿的信号控制方式。四相位信号控制交叉口中,某一进口道非机动车分别采用2种左转方式后与机动车发生冲突的冲突点示意图如图3所示。从图3可以看出,在四相位信号控制交叉口中,左转方式1共有2处机非交叉冲突点;左转方式2通过无导流岛交叉口时共有4处机非冲突点;左转方式2通过有导流岛交叉口时共有2处机非冲突点。
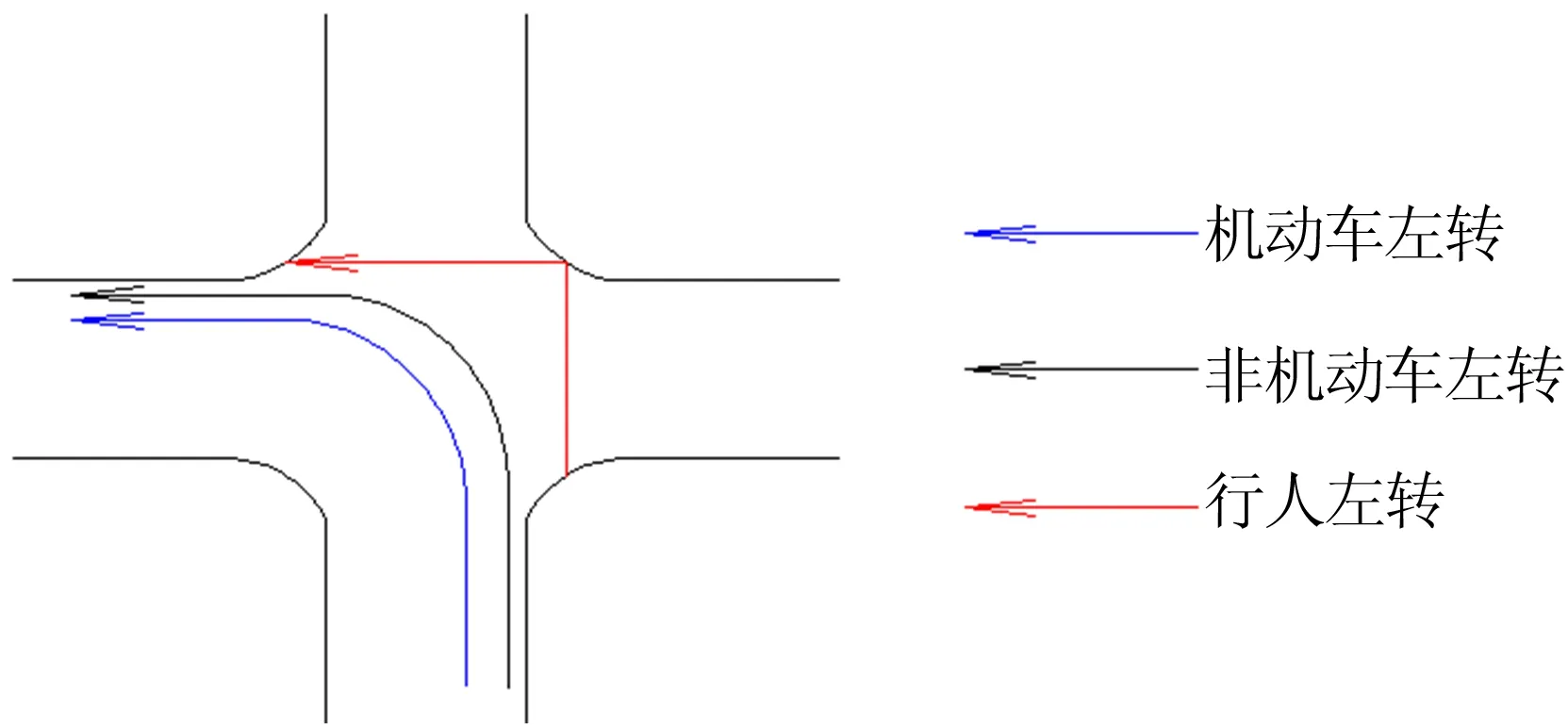
图1 非机动车与机动车采用相同方式通过(方式1)
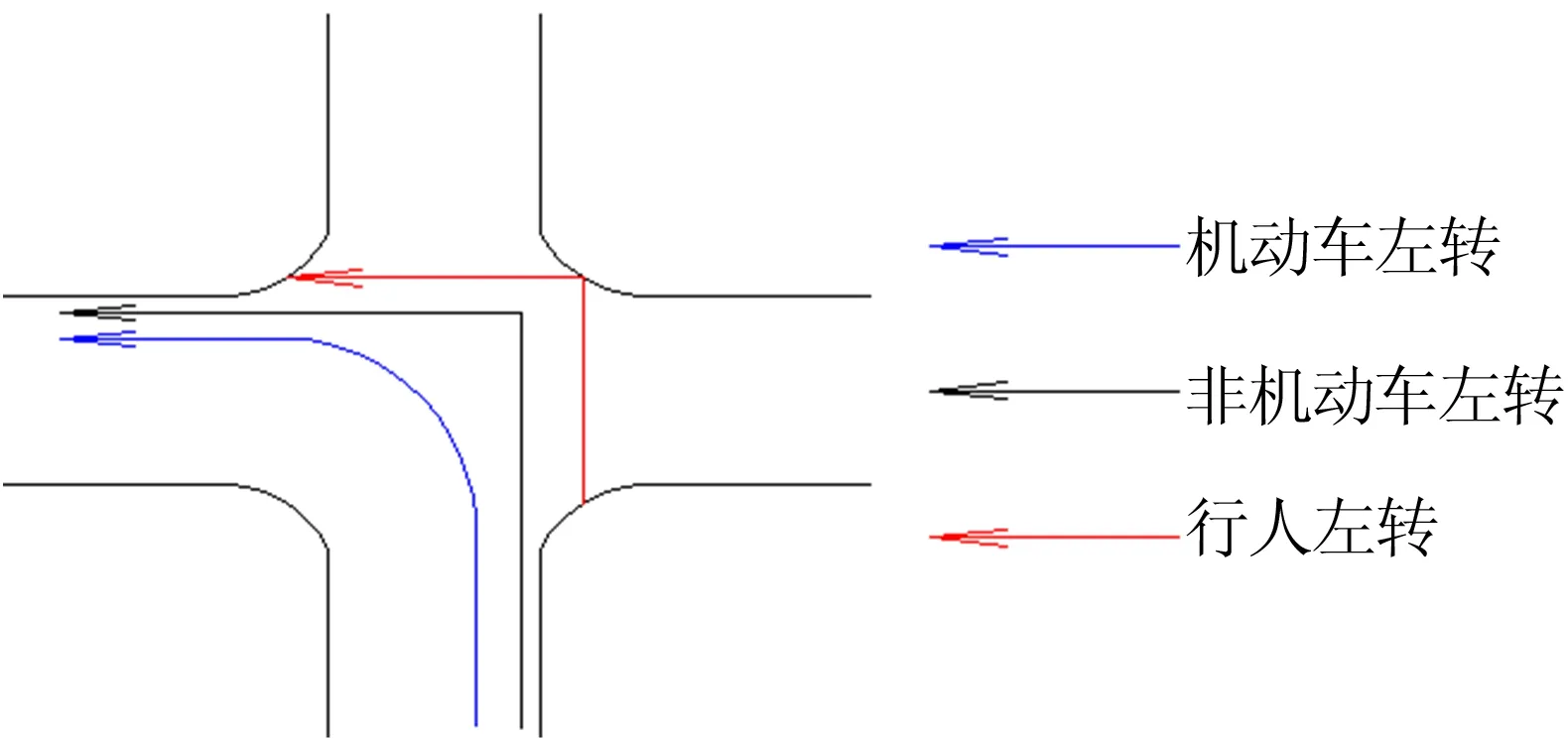
图2 非机动车与行人采用相同方式通过(方式2)

图3 四相位信号控制交叉口机非冲突点
1.2 交叉口左转非机动车与机动车膨胀冲突
非机动车的膨胀效应是指在信号交叉口某一进口道非机动车无通行权期间内,非机动车在停止线后排队等候。此时非机动车较为密集,横向占用宽度较小。当转至绿灯信号后,非机动车加速驶入交叉口,其横向宽度要求增大,非机动车流向两侧扩张,车流整体呈扩散状态。
非机动车流的膨胀效应将与同向行驶的机动车产生冲突。因此,分析非机动车膨胀现象、建立非机动车膨胀模型是研究非机动车膨胀现象与同向机动车产生冲突的基础。交叉口左转非机动车膨胀效应如图4所示。
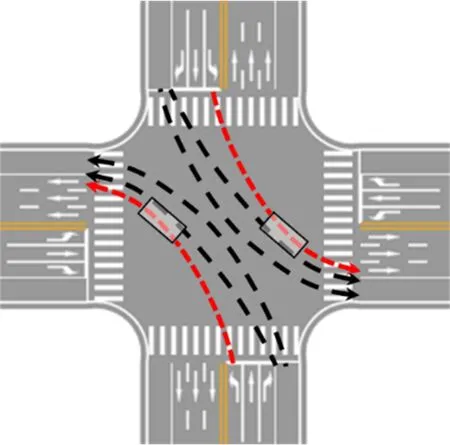
图4 交叉口左转非机动车膨胀效应
2 机非冲突对机动车通行能力的影响
2.1 机非交叉冲突对交叉口通行能力的影响
在四相位信号控制交叉口,机非交叉冲突过程较为复杂,其影响可归结为以下2类:
(1) 绿灯初期非机动车占用冲突区影响。在绿灯初期,非机动车由于加速性能较好,先于机动车进入机非冲突区。该时段内,机动车无法驶入冲突区,需等待已驶入冲突区内的非机动车驶离后方可进入,实际通行能力降低。
(2) 非机动车穿越冲突区造成的影响。当机动车流占据冲突区时,非机动车将利用可接受穿越时间间隙穿越冲突区,因此,即将驶入冲突区的机动车会采取制动措施避免与前车相撞,进而降低整体机动车流速度。而当非机动车全部穿越冲突区后,机动车流将加速通过冲突区。此时段内,机动车的速度波动进一步降低其通行能力。
2.1.1 非机动车到达分布分析
城市道路交叉口非机动车的到达可用离散型分布进行描述。离散型分布主要有泊松分布、二项分布及负二项分布3种。其中,泊松分布常用于描述交通量不大且没有交通信号干扰的车辆到达分布,而在国内的城市道路上,非机动车交通量大,且存在着交通信号及其他因素干扰,不适宜用泊松分布描述。因此,本文采用二项分布和负二项分布描述不同状态下的自行车到达。
当非机动车流交通量大,自由行驶机会少时,可用二项分布描述该交通流,即
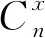
(1)
p=(m-S2)/m
(2)
n=m2/(m-S2)
(3)
其中:P(x)为非机动车道进口道周期内到达x辆非机动车的概率;x为非机动车道进口道周期内到达的非机动车数量;m为样本均值;S2为样本方差。
而当非机动车流波动性较大亦或计数周期包含高峰时段和非高峰时段时,负二项分布拟合观测数据较为准确:
(4)
p=m/S2
(5)
k=m2/(S2-m)
(6)
2.1.2 绿灯初期非机动车占用冲突区影响分析
对绿灯初期非机动车占用冲突区的时间进行分析。令非机动车在绿灯初期通过冲突区所需时间为T1。密集通过冲突区的车辆是在红灯时间Tr和T1内累积的,可以得出:
(Tr+T1)λn=NtBT1
(7)
(8)
其中:λn为非机动车到达率,非机动车整体到达分布呈二项分布或负二项分布;Nt为冲突区非机动车断面饱和流率,建议值为0.061 3辆/(s·m)[13];B为冲突区非机动车流宽度。
在T1时段内,机动车无法通过冲突区,需等待冲突区内全部非机动车离开后方可通行[14]。假设非机动车到达分布呈负二项分布,则在某时段T2内,冲突区无非机动车到达的概率为:
(9)
令Tg为有效绿灯时间,则冲突区无非机动车的时间为P0(Tg-T1)。设机动车流以流率q0通过冲突区,则可得出周期内机动车在冲突区无非机动车时段通过的交通量为:
Qn=q0P0(Tg-T1)/3 600
(10)
2.1.3 非机动车穿越冲突区造成的影响分析
对非机动车穿越机动车流造成的影响进行分析,根据交通流理论可得出机动车车流的流率均值[15]为:
(11)
其中:v1、v2为机动车流减速前、后的平均速度;q(v)为机动车交通量关于速度v的函数。
令非机动车通过冲突区的时间为T3,则非机动车一次穿越过程中能通过的车辆数为:
z=2q12T3
(12)
冲突区有非机动车穿越的概率P1应为非机动车到达冲突区,且机动车车辆中存在非机动车可接受穿越时间间隙的概率。假设机动车与非机动车到达相互独立,则
z=P(x>0)P(t≥tnt)=
(1-P(x=0))P(t≥tnt)
(13)
其中:t为机动车流车头时距;tnt为非机动车可接受穿越时间间隙。
假设机动车流车头时距t服从移位负指数分布,则可得在时段T2内P1为:
(14)

(15)
因此,机动车流在非机动车穿越影响时段内通过的车辆数Qi为:
(16)
2.1.4 机非交叉冲突区机动车通行能力研究
根据上述分析可以得出,在机非交叉冲突区的非机动车影响下,机动车通行能力为:
Qc=(Qn+Qi)(3 600/C)
(17)
其中,C为交叉口信号周期时长。
则可求得非机动车与机动车交叉冲突对机动车通行能力影响系数为:
(18)
2.2 机非膨胀冲突对交叉口通行能力的影响
在信号控制交叉口,若非机动车直接左转通过交叉口,则控制信号转至左转相位时,左转机非车辆同时放行。当左转非机动车交通量较小时,非机动车膨胀对机动车产生的影响极小;但随着左转非机动车交通量的增加,车流膨胀宽度也将增大,直接降低同向进口道左转机动车通行能力。
利用南京市“珠江路-太平北路”与“中山北路-模范中路”2个交叉口的航拍视频进行机非膨胀冲突的影响研究,分析直接左转非机动车最大横向行驶宽度Bmax和左转机动车通过交叉口时间之间的关系。研究得出,当Bmax为2.5 m及以下时,左转机动车几乎不受影响。但是随着Bmax增大,机动车左转通过交叉口的平均时间逐渐增大,此时Bmax和机动车左转通过交叉口的时间呈正相关关系。
同向进口道左转机动车间受左转非机动膨胀冲突影响,通过交叉口时延误增加,通行能力降低。经过相关交叉口实测调查,左转机动车无左转非机动车影响直接通过交叉口的平均时间为10.48 s,则可得出左转非机动车不同Bmax的情况下,机动车通过交叉口时间延误t延与左转机动车的通行能力调整系数f膨,见表1所列。

表1 不同Bmax下的t延与f膨
左转机动车f膨可应用于交叉口左转机动车饱和流率及通行能力的调整。左转非机动车Bmax增加将不断降低左转机动车通行能力,但由于交叉口空间资源有限,交叉口左转非机动车Bmax有极限值。通过多次观测调查,左转非机动车Bmax约为7.0 m。在左转非机动车横向行驶宽度达到6.5 m以上时,左转非机动车流会占据交叉口核心区域,并截断左转机动车流。
3 交叉口机非冲突数模型构建
本文通过对南京市“珠江路-太平北路”与“中山北路-模范中路”2个交叉口的实地调查,获取机动车交通量、非机动车交通量、机非交叉冲突数等相关数据,构建机非交叉冲突数模型。
文献[16]构建了交叉口3种类型机非交通冲突的冲突数预测模型,机非交通冲突的3种类型分别为:
类型1同向进口道右转机动车与直行非机动车交通冲突。
类型2相邻进口道右转机动车与直行非机动车交通冲突。
类型3对向进口道左转机动车与直行非机动车交通冲突。
3种类型机非交通冲突的冲突数预测模型[16]为:
(19)
(20)
(21)
其中:ui为3种类型机非交通冲突数的预测值(i=1,2,3);X机动车i为3种类型机非交通冲突的机动车交通量(i=1,2,3);X非机动车i为3种类型机非交通冲突的非机动车交通量(i=1,2,3)。
文献[16]通过构建机动车与非机动车交通量的广义线性机非交通冲突模型,预测3种机非交通冲突数,但该模型中非机动车的影响因素只考虑总体交通量,未考虑自行车和电动自行车的差异性。
3.1 交叉口机非交叉冲突数模型构建
针对四相位信号控制交叉口构建左转非机动车与机动车交叉冲突数模型,分析左转非机动车与机动车交叉冲突点,主要有2处:① 左转非机动车与同向进口道右转机动车交叉冲突(冲突点1);② 左转非机动车与对向进口道右转机动车交叉冲突(冲突点2)。
构建冲突点1的交叉冲突数模型为:
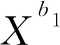
(22)
其中:C1为冲突点1的交叉冲突数;X同右机为同向进口道右转机动车交通量;X自为左转自行车交通量;X电为左转电动自行车交通量;a1、b1、d1、e1为相关系数。
以15 min为时间间隔获取冲突点1的C1、X同右机、X自、X电数据,见表2所列。

表2 冲突点1的交叉冲突数模型数据
将表2数据代入(22)式,得到模型为:
(23)
为检验该模型的预测能力,利用2组相关数据进行模型校核,相关数据和由(23)式预测的冲突数见表3所列。

表3 冲突点1的交叉冲突数模型校核结果
从表3可以看出,该交叉口冲突点1的交叉冲突数模型(23)式预测能力较好,能够反映此冲突的实际状况,可应用于冲突预测和交叉口安全评价。
建立冲突点2的交叉冲突数模型为:

(24)
其中:C2为冲突点2的交叉冲突数;X对右机为对向进口道右转机动车交通量;a2、b2、d2、e2为相关系数。
以15 min为时间间隔获取冲突点2的C2、X对右机、X自、X电数据,见表4所列。
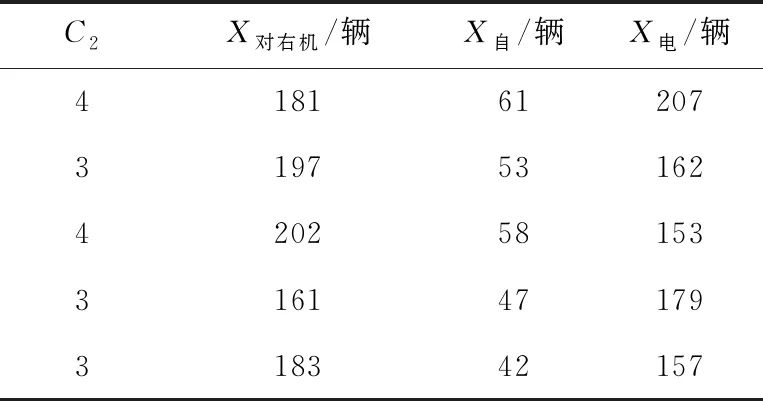
表4 冲突点2的交叉冲突数模型数据
将表4数据代入(24)式,得到模型为:
(25)
为检验该模型的预测能力,利用2组相关数据进行模型校核,相关数据和由(25)式预测的冲突数见表5所列。

表5 冲突点2的交叉冲突数模型校核结果
从表5可以看出,该交叉口冲突点2的交叉冲突数模型(25)式预测能力较好,能够反映此冲突的实际状况,可应用于冲突预测和交叉口安全评价。
3.2 交叉口机非膨胀冲突数模型构建
通过分析机非膨胀冲突的产生机理,得到影响交叉口左转机动车与非机动车膨胀冲突的3个最直接因素,分别为机动车交通量、非机动车交通量及交叉口渠化状况。
建立交叉口左转非机动车与同向进口道左转机动车膨胀(简称“左转膨胀点”)冲突数模型为:
(26)
其中:C3为左转膨胀点的冲突数;X同左机为同向进口道左转机动车道交通量;D1为交叉口进口道最外侧左转机动车道外侧边线至非机动车道内侧边线的距离;a3、b3、d3、e3为相关系数。
以1 h为时间间隔获取左转膨胀点的C3、X同左机、X自、X电、D1数据,见表6所列。
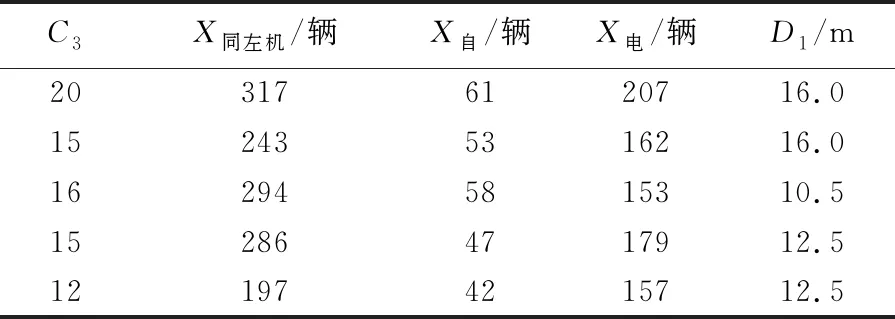
表6 左转膨胀点冲突数模型数据
将表6数据代入(26)式,得到模型为:
(27)
为检验该模型的预测能力,利用2组相关数据进行模型校核,相关数据和由(27)式预测的冲突数见表7所列。
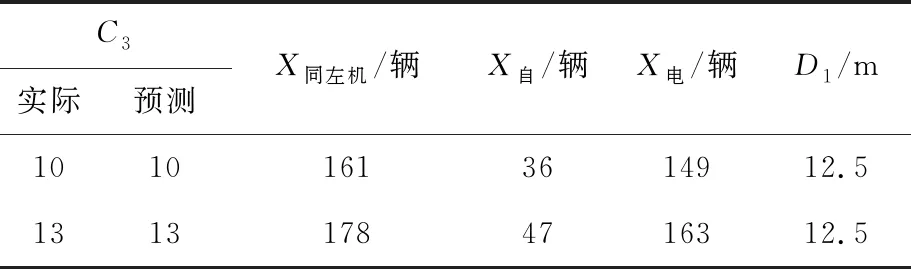
表7 左转膨胀点冲突数模型校核结果
从表7可以看出,该交叉口左转膨胀点冲突数模型(27)式预测能力较好,能够反映此冲突的实际状况,可应用于冲突预测和交叉口安全评价。
4 结 论
本文从交通冲突的角度出发,研究交叉口左转非机动车与机动车冲突原理,将非机动车对机动车通行能力的影响细分为绿灯初期非机动车占用冲突区影响与非机动车穿越冲突区造成的影响;进一步构建机非交叉冲突和膨胀冲突的冲突数模型,通过实测数据进行拟合,得出不同冲突下交叉口左转机动车通行能力影响系数。
相关冲突和各优化方法对非机动车通行效率的影响对于交叉口的整体优化同样具有重要的意义,下一步研究将综合考虑这些影响因素,使得优化方法能令交叉口整体优化度最好。
