解三角形中的最值、范围问题

◇ 山东 冯海侠

在新高考形势下,“解三角形”应该会出现在第17题或第18题的位置,一般都属于中等或中等偏下难度的题目,是学生必拿分的题．高考对正弦定理和余弦定理的考查较为灵活,题型多变、综合性强,有利于培养学生的创新意识．这类问题简单,但部分学生却拿不到满分,尤其是求最值或范围的问题．下面笔者以两道高考题为例来归纳这类问题的解答方法及技巧,希望能帮助读者突破瓶颈,提高学习效率．

例1(2019年全国卷Ⅲ理18)△ABC的内角A,B,C的对边分别为a,b,c,已知bsinA．

(1)求B；

(2)若△ABC为锐角三角形,且c＝1,求△ABC面积的取值范围．

解析

又因为B∈(0,π),所以,则0,所以,则,即

所以

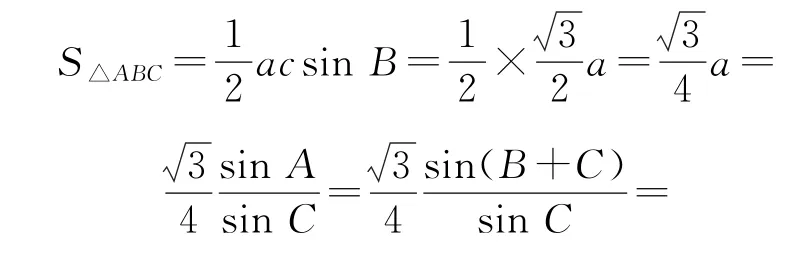
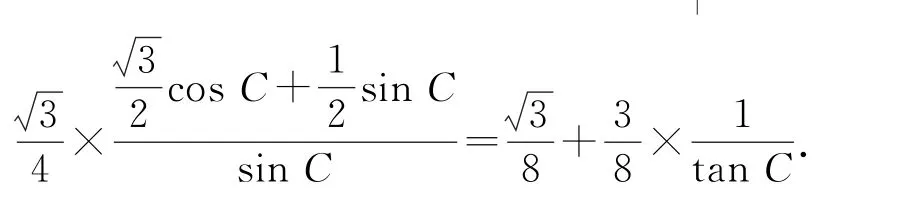
又因为△ABC是锐角三角形,故且,所以则,即,所以

例2(2013年全国卷Ⅱ理17)△ABC的内角A,B,C的对边分别为a,b,c,已知a＝bcosC＋csinB．

(1)求B；

(2)若b＝2,求△ABC面积的最大值．

解析

(1)由已知条件及正弦定理得

又因为A＝π－(B＋C),故

由①②得sinB＝cosB,又B∈(0,π),所以

(2)△ABC的面积,由已知条件及余弦定理得,故当且仅当a＝c时,等号成立．因此,即△ABC面积的最大值为

解三角形中的最值及范围问题主要有两种方法,其一是利用基本不等式求最大值或最小值,这类问题多与余弦定理相结合,常见形式如下．

(1)a2＝b2＋c2－2bccosA≥2bc－2bccosA,从而求出bc的最大值；

在使用基本不等式时一定不要忘了等号的验证,同时,要将所求式子转化为含有一个未知数的函数,大多情况下是转化成关于某个角的函数,利用三角函数性质及角的条件求解,有时也转化为某个边的函数,再结合边的范围求解．解三角形中的最值和范围问题是重点也是难点,综合性较强,所以学生不仅要有扎实的基本功,还要灵活应变,掌握做题技巧,这样在高考中才能取得满意的成绩．