空间立体几何中的外接球问题
2021-01-29新疆苏伦高娃
◇ 新疆 苏伦高娃
球是一种重要几何体,由于球自身的完美对称性,常常与一些简单几何体(如柱、锥、台)结合,求外接球的表面积、体积,这是高考考查的重点和难点.这一类问题,学生的得分率较低,大部分学生都不知道如何下手,归根结底在于学生对空间问题的想象能力、推理能力和计算能力都有所欠缺.对此本文来谈谈笔者是如何在教学过程中引导学生解决此类问题的.
预备知识:
1)球心和截面圆心的连线垂直于截面;
2)球心到截面的距离d与球的半径R及截面的半径r满足:R2=d2+r2;
3)圆的直径所对的圆周角为直角.
1 正方体或长方体的外接球
例1 已知各顶点都在同一个球面上的长方体的三条棱长分别为1,2,3,则此球的表面积为_______.
解析
要求球的表面积,只需求出长方体外接球的半径,所以应先确定球心的位置,求出球的半径.
因为外接球球心就是长方体体对角线的中点,半径是长方体体对角线长的一半,即,求得外接球的半径后,代入球的表面积公式S=4 πR2,可得球的表面积为14 π.
问题:在上题中,以长方体中任意不共面的四个顶点为顶点,可以构成什么样的几何体?有哪几种?它们的外接球是怎样的?
笔者在这个环节中提前准备了学案,给学生充分的时间去构造空间四面体(如图1).
通过直观感受和交流讨论,学生能够顺利推出四面体的外接球和长方体的外接球是同一个球,从而四面体的外接球问题可转化为长方体的外接球问题进行求解.

图1
例2《九章算术》中,将底面为长方形且由一条侧棱与底面垂直的四棱锥称之为阳马;将四个面都为直角三角形的三棱锥称之为鳖臑.若三棱锥P-ABC为鳖臑,PA⊥平面ABC,PA=AB=2,AC=4,三棱锥P-ABC的四个顶点都在球O的球面上,则球O的表面积为________.
解析
本题的求解思想就是将三棱锥P-ABC放入长方体中,如图2,三棱锥的外接球就是长方体的外接球.因为PA=AB=2,AC=4,△ABC为直角三角形,所以.设外接球的半径为R,由题意得,故球的表面积为20 π.

图2
特别地,当长方体为正方体时,还可以利用正方体的性质求解外接球问题.
例3已知三棱锥P-ABC中,PA,PB,PC两两垂直,且长度相等.若点P,A,B,C都在半径为1的球面上,则球心到平面ABC的距离为________.
解析
如图3,因为PA,PB,PC两两垂直,故正三棱锥P-ABC的外接球就是以PA,PB,PC为棱的正方体的外接球.球心在正方体体对角线的中点上,根据正方体的性质,平面PBC具有很多良好的性质,如体对角线PD⊥平面ABC,垂足是PD的一个三等分点,所以球心到平面ABC的距离为半径的
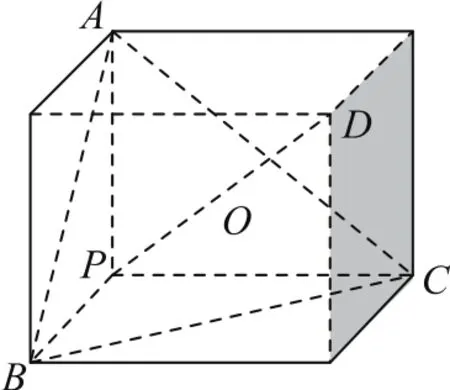
图3
2 求与棱柱外接球有关的计算问题
例4设正三棱柱的侧棱垂直于底面,所有棱长都为a,顶点都在一个球面上,则该球的表面积为_______.
解析
如图4所示,P为三棱柱底面中心,O为球心,易知则球的半径满足R2=AO2=AP2+,所以,球的表面积为

图4
3 求与棱锥外接球有关的计算问题
例5已知球O是三棱锥S-ABC的外接球,△ABC是边长为1的等边三角形,SC是球O的一条直径,SC=2,则三棱锥S-ABC的体积为________.
解析
因为三棱锥S-ABC和三棱锥O-ABC有共同的底面ABC,球心O为SC的中点,所以三棱锥S-ABC的高为三棱锥O-ABC高的2倍,即VS-A B C=2VO-A B C.
如图5所示,三棱锥O-ABC的棱长都是1,取等边△ABC的中心D,点D即为底面ABC外接圆(即截面圆)的圆心,球心O在点D的正上方,则OD⊥平面ABC.因为截面圆半径,因为球的半径R=OC=1,则

图5

所以

从近几年的高考试题来看,经常出现与外接球有关的问题,本文结合笔者在教学过程中的做法,推广出与外接球有关问题的具体解法,以便学生比较容易地掌握球的性质及与外接球有关的计算问题.
