知其然,知其所以然———以立体几何问题为例谈思路寻找

◇ 山东 臧书华

教师在教学中常会遇到这样的情况：对于一道学生没有思路的问题,教师讲解后学生能立刻明白求解方法,但再遇到类似的问题时,却无从下手．究其原因,发现学生听教师讲解后,明白题目应该这样求解,但不清楚为什么要这样求解,也就是说对于解题思路是如何产生的并不明确．本文以一道立体几何问题为例,谈一谈解题思路寻找的历程．

例如图1所示,正方体ABCD-A1B1C1D1的棱长为2,点O为底面ABCD的中心,点P在侧面BB1C1C的边界及其内部运动．若D1O⊥OP,则△D1C1P面积的最小值为( )．

图1

本题是一道以正方体为背景的动态几何问题,旨在考查学生对空间几何体性质的识别能力,以及空间平行、垂直关系的判定与性质的应用能力．求△D1C1P面积的最小值,关键是确定点P的位置．

1 分析条件,确定方向

欲确定点P的位置,需要分析点P满足的关系．点P在侧面BB1C1C的边界及其内部运动,且D1O⊥OP．D1O为定线,OP为动线,据此可知OP在一个与D1O垂直的平面内,因此构造这个平面是寻找点P位置的关键．构造的原理是利用线面垂直的判定定理,即一条线与一个平面内的两条相交直线垂直,则线面垂直．在构造的过程中,往往会多次利用线线、线面、面面平行或垂直的推导关系．

类似地,若某一问题中出现一条变动的直线与一个确定的平面平行,根据面面平行的性质(即由一个平面内的直线与另外一个平面平行,可知该直线在一个与已知平面平行的平面内),因此可结合已知几何体的结构特征,构造这个平面,从而确定动线所在的位置．

2 依托背景,探究关系

通过添加辅助线,构造与D1O垂直的平面,要充分挖掘正方体的有关性质．正方体是特殊的空间几何体,蕴含着丰富的性质．其中面对角线与相应的对角面垂直,如AC⊥平面BDD1B1．过同一顶点的三个面对角线构成的平面与过该顶点的体对角线垂直,如BD1⊥平面ACB1,且BD1与平面ACB1的交点为BD1的三等分点．

正方体的各个侧面均为正方形,正方形中除了四个角均为直角,对角线垂直以外,还存在一些重要的性质,如图2所示,在正方形BCC1B1中,若E,F分别为BB1,BC的中点,利用平面几何的性质可证得CE⊥C1F,这些关系都是构造辅助线的基础．

图2

3 关系明了,水到渠成

明确了上述原理,构造辅助线也就水到渠成了．如图3所示,连接OC,由正方体的性质AC⊥平面BDD1B1,而D1O⊂平面BDD1B1,所以OC⊥D1O．

取BB1的中点E,BC的中点F,连接CE,C1F．由上述分析可知C1F⊥CE,而由正方体的性质可知D1C1⊥平面BCC1B1,所以D1C1⊥CE．因为D1C1∩C1F＝C1,所以CE⊥平面DD1C1F,而D1O⊂平面DD1C1F,所以D1O⊥CE,又CE∩CO＝C,所以D1O⊥平面OCE,因此D1O垂直平面OCE内的任意一条直线,所以OP在平面OCE内,则点P在线段CE上．

在△D1C1P中,D1C1＝2,D1C1⊥C1P,△D1C1P面积最小,则C1P取得最小值．由图3易知当点P为C1E,CF的交点时,C1P取得最小值．

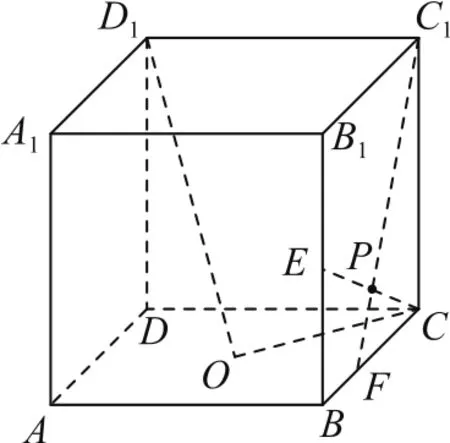
图3

由正方形的性质可知△C1PC∽△C1CE,故,即,所以,所以此时△D1C1P的面积为．故选B．

综上,问题的求解不仅要知其然,更要知其所以然,这样在面对一道新问题时,才能顺利找到切入点．