基于COMSOL的静态仓储稻谷粮堆温度场模拟研究

葛蒙蒙，陈桂香，刘文磊，刘超赛

河南工业大学 土木工程学院，河南 郑州 450001

仓储环境的温湿度是影响粮食品质的主要因素，粮食本身的生命活动与粮仓内外环境间的热量传导影响粮堆的温湿度[1-2]。因此，掌握并准确预测仓储粮堆的温度变化是确保粮食安全储藏的基础。由于粮食在储藏过程中受到生物和非生物因素的多重影响，仓储粮堆温度变化难以得到准确、有效地预测。

研究粮堆热湿传递规律方法有试验和数值模拟两种。试验结果往往是可靠的，但试验过程会比较烦琐，甚至需要投入大量的人力、物力资源，而且每次试验得出的结果不尽相同，具有不可重复性。数值模拟可以很好地解决试验方面的不足，它可以准确有效地分析和预测粮仓生态系统的变化。Thorpe等[3]在分开考虑仓储粮堆间气体温度和粮食本身温度的情况下，建立了仓储粮堆温度变化的数学模型。Jia等[4]构建了笛卡尔坐标系下的圆筒仓粮堆温度场模型。Gaston 等[5]利用有限元法，模拟了在外界环境季节性变化以及小麦的呼吸作用下，小麦粮堆温度和水分变化规律。张前等[6]根据试验回归模型预测仓储粮堆的温度变化。李军军等[7]依据有限元法建立了仓储粮堆温度场数学模型。蒋华伟等[8]构建了在单一局部发热下的仓储粮堆温度场的数学模型。梁醒培等[9]利用数值模拟的方法建立了小麦粮堆的温度场数学模型，并且研究了小麦在不同季节的温度变化。门艳忠[10]利用有限元分析法和传热学相关理论模拟了非稳态下稻谷的温度变化，结果表明粮堆内会出现一个相对高温区，但由于其数学模型不够精细，所以与实际情况有一定的差距，不能很好地应用于实际。刘建英[11]根据实仓内3个高度层的测温数据，推导出粮温经验公式，但其仅能反映仓内局部的温度，并不能精确地反映仓内其他位置的温度变化。周全申等[12]通过现场实测，统计分析了不同气候条件对粮堆温差的影响。闫艳霞等[13]依据热力学相关理论与平衡理论等构建了局部发热条件下的粮堆温度场数学模型，发现仓储粮堆温度总是处于一种动态变化当中。白忠权[14]在考虑谷物吸附和解吸的情况下，利用数值模拟与试验验证，得出谷物粮堆传热传质的变化规律。

作者利用COMSOL软件建立静态储粮的平房仓三维物理模型，对粮仓以及粮堆的传热过程进行数值模拟,分析了仓储稻谷粮堆整体平均粮温变化，并与实测数据进行对比。

1 模型模拟

1.1 平房仓三维物理模型

模拟仓为浙江某高大平房仓，平房仓长29.37 m，宽20.44 m，高8.2 m，粮堆高6 m。墙体采用空心砖墙结构，仓顶采用预应力混凝土板，仓底为混凝土地面。利用COMSOL软件建立高大平房仓三维物理模型，模拟计算域由粮堆与仓内上部空气层两个体区域组成。对物理模型采用非结构网格极细化处理，共划分为170多万个网格。粮仓模型及网格划分如图1所示。

图1 高大平房仓三维物理模型及网格划分Fig.1 Three-dimensional physical model and mesh division diagram of large horizontal warehouse

1.2 模拟参数

1.2.1 粮堆外界环境温度

对于静态储粮，引起粮堆温度变化的主要因素是外界环境温度的变化。将模拟仓2017年外界月平均气温变化绘成曲线，结果如图2所示。

图2 浙江某高大平房仓2017年外界月平均气温变化Fig.2 Average temperature change outside a large horizontal warehouse in Zhejiang province in 2017

对图2曲线进行近似拟合得出外界温度变化函数：

T=-0.606 4(t/2 592 000-7.07)2+197.42，

式中：T为外界环境平均温度,K；t为时间,s。

仓壁和粮堆的初始温度取自2016年12月底的平均温度，全年环境温度变化采用上式所示温度，每月按30 d进行计算。

1.2.2 粮仓壁面边界

静态储粮过程中，粮仓壁面的温度变化会直接影响粮堆温度。外界环境通过改变仓壁温度，进而影响粮堆温度。在长时间自然储粮过程中，外部的传热主要是热辐射与对流换热，在考虑太阳辐射条件时，粮仓仓壁与其仓顶所受太阳辐射量不尽相同，此时模拟计算过程不仅复杂且结果会产生很大误差。为简化计算，将仓壁与仓顶所受太阳辐射转化为仓壁温度，仓底部为绝热层。

1.2.3 模型参数

COMSOL模拟静态储粮传热过程，研究发现影响粮堆传热计算的主要参数有稻谷堆的导热系数、比热容、密度与孔隙率等。具体参数值如表1所示[15]。

表1 COMSOL数值模拟的相关条件和材料参数设置Table 1 Relevant conditions and parameter settings of COMSOL numerical simulation

1.3 控制方程

稻谷储藏期间涉及的方程有质量守恒、动量守恒以及能量守恒方程。

质量守恒方程：

式中：ρa为空气密度，kg/m3；t为时间，s；u为风速，m/s。

动量守恒方程：

式中：μ是空气动力黏度，Pa·s；K为渗透率,m2；g为重力加速度，m/s2；β是空气膨胀系数,1/K；δij为kronecker函数;T为稻谷粮堆的温度，K；T0为初始温度，K；p为压强，Pa。

能量守恒方程：

式中：ρg为稻谷粮堆的干密度，kg/m3;Cg为稻谷粮堆的比热容，kJ/(kg·K);Ca为空气的比热容，kJ/(kg·K)；Kg为稻谷粮堆的导热系数，W/(m·K)；Wg为干基水分；hfg是粮堆的蒸发潜热，kJ/kg；qh是呼吸过程释放的热量，J/mg；YCO2是粮堆呼吸24 h的CO2的释放率。

在自然储藏过程中不存在强制的通风过程，所以不用考虑粮堆与孔隙间的气流温差，进而可忽略由温度变化引起的自然对流传热。粮仓中以仓壁与粮堆间的热传导为主，其热量传导的数学模型：

Q=-kT，

式中：Q为热通量密度，kJ/(m2·s)；k为粮堆的热传导系数，W/(m·K)；T为粮堆的温度，K。

2 结果与分析

2.1 粮仓宽度方向上粮堆的温度分布

图3为模拟粮仓在宽度方向上中间垂直截面的温度分布变化情况。

图3 粮仓宽度方向中垂面温度分布变化情况Fig.3 Variation of vertical temperature distribution in the width direction of the warehouse

由图3可知，稻谷粮堆温度沿粮仓宽度方向呈现出很明显的不均匀分布。储藏前3个月，近壁面粮堆温度随外界环境温度上升逐渐上升，并逐渐向粮堆内部传递；储藏6个月时，随着外界环境温度值的进一步升高，距壁面稍远处粮堆温度也随之上升；储藏9个月时，此时外界环境温度虽然已经开始下降，但除近壁面粮堆温度略有下降外，粮堆内部温度仍有上升趋势；储藏12个月时，随着外界环境温度的持续下降，近壁面粮堆温度也随之下降，但由于内部热量不能及时传递出去，近壁面会出现相对高温区。仓顶空气层是粮堆上层没有出现高温区的主要原因，是由于空气热传导性弱于仓顶混凝土，所以能够在一定程度上稳定粮堆的温度。

2.2 粮仓长度方向上粮堆的温度分布

图4为模拟粮仓在长度方向上中间垂直截面的温度分布变化情况。由图4可知，粮仓长度方向上稻谷粮堆的温度变化情况与宽度方向上相似，但不同方向上粮堆温度变化受外界环境影响程度不同，粮仓长度方向上粮堆高温带的范围和规模均小于宽度方向。因此，在静态储藏过程中，外界环境对粮堆温度在粮仓宽度方向上的影响要大于长度方向。

图4 粮仓长度方向中垂面温度分布变化情况Fig.4 Variation of vertical temperature distribution in the length direction of the warehouse

为了更直观地分析稻谷粮堆内部温度分布及变化情况，选取堆高为3 m平面上沿长度方向的中轴线研究粮堆温度的变化情况，结果如图5所示。

图5 3 m处粮堆中轴线沿粮仓长度方向温度分布Fig.5 Temperature distribution of the central axis of the grain pile at 3 m along the length of the warehouse

由图5可知，2—8月，近壁面处稻谷粮堆温度最高，越往中间，粮堆温度越低，尤其是6—8月最为明显，此时外界环境逐渐达到1年中的最高温，近壁面处粮温很快达到全年最高值24.1 ℃。9—12月，此时外界环境越过1年中的最高温开始下降，近壁面处高温粮堆温度也随之开始下降，但其积聚的热量则继续向内传递，这样就出现粮堆温度由壁面往内迅速上升，达到最大值后逐渐下降的现象。在距粮仓壁面1～3 m处，粮堆产生了明显的高温区，且在12月最为显著，距粮仓壁面约2 m处高温带温度达到峰值。在距粮仓壁面较远处的粮堆随储藏时间延长，其粮温有所提高，储藏12个月的最高粮温为14.7 ℃。在距壁面4 m左右，无论是长度方向还是宽度方向上，粮温始终处于一个稳定的低温区。

2.3 试验验证

为验证构建的研究模型，将仓储稻谷粮堆整体平均粮温实测数据与模拟结果进行比较分析，试验时用粮情检测系统测定高大平房仓稻谷粮堆温度的变化，将高大平房仓1年内稻谷粮堆整体平均温度模拟结果和实测结果对比，如图6所示。

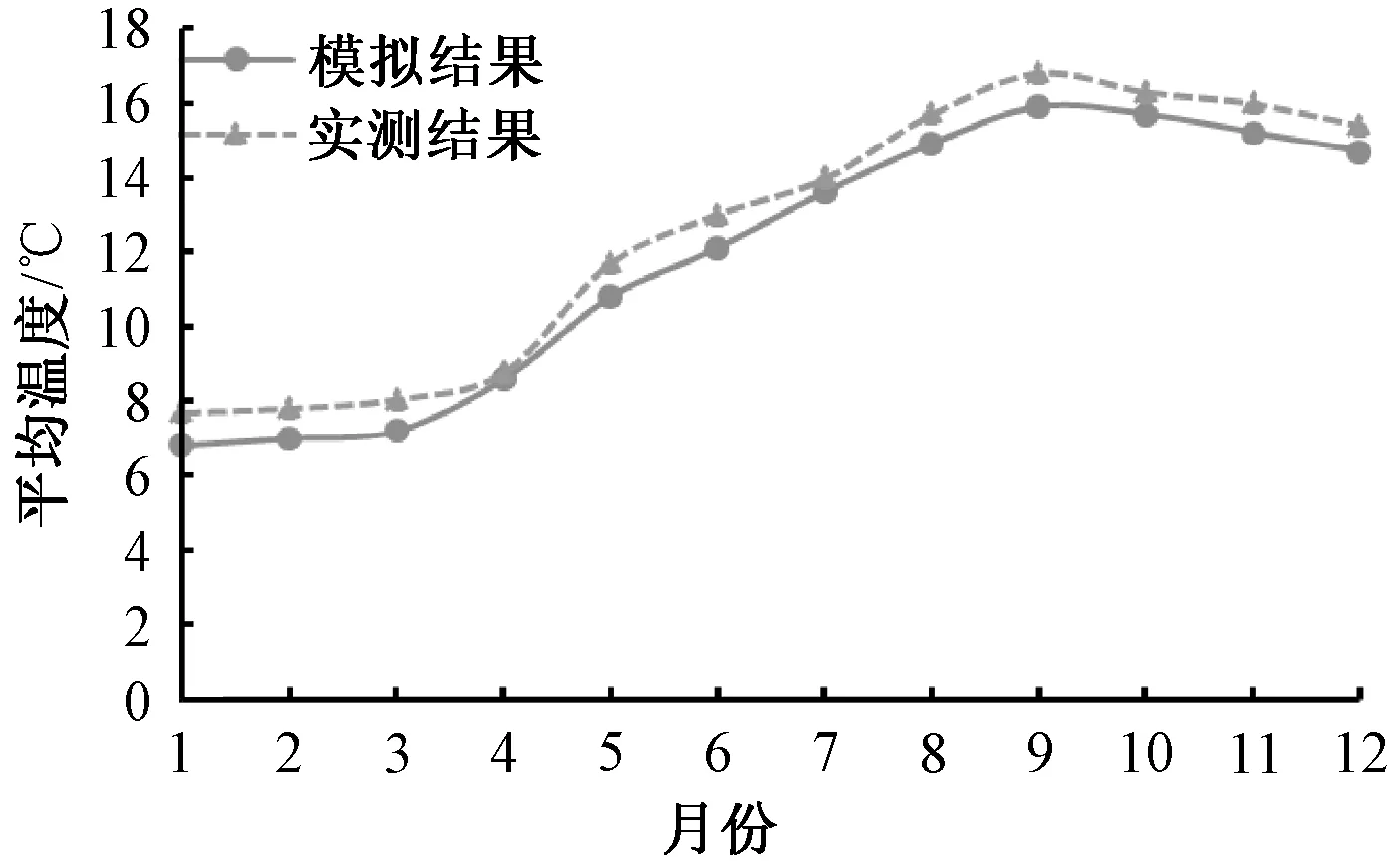
图6 高大平房仓一年内粮堆平均温度变化模拟与实测对比结果Fig.6 Comparison of simulated and measured results of average temperature change of grain pile in a large warehouse within one year

由图6可知，模拟与实测结果变化趋势基本一致，粮堆温度实测值略高于模拟值，最大误差为0.91 ℃，在误差允许范围内。

3 结论

利用COMSOL软件对静态储藏稻谷粮堆1年内的温度变化进行了研究，得出如下结论：在静态储粮过程中粮仓外界环境尤为重要，粮堆温度受外界温度变化而改变。近壁面处粮温受外界环境温度变化影响最为显著，在距粮仓壁面较远处的粮堆随储藏时间延长，其粮温有所提高。当外界环境温度经过由低到高再到低的变化后，在距粮仓壁面1～3 m处，稻谷粮堆产生了明显的高温区。粮仓长度方向上稻谷粮堆的温度变化情况与宽度方向上相似，但在静态储藏过程中，外界环境对粮堆温度在粮仓宽度方向上的影响要大于长度方向。将模拟与实测结果对比可知，两者变化趋势基本一致，稻谷粮堆温度实测值略高于模拟值，最大误差为0.91 ℃。利用COMSOL对粮堆温度传递进行模拟是一种简便且有效的途径，可以为今后的优化工作提供更加直观可靠的研究工具。