情境融合拓展思维
2021-01-21陈静
陈静







【摘要】 学生千差万别,每个人都有自己的性格,他们有的学习能动性很强,有的学习兴趣不高,故教师需要对他们的学习情况逐个分析.在初中数学教学中,采用情境融合的教学方式可以充分调动学生的学习兴趣,提高他们合作探究的欲望.本文主要以初中数学锐角三角函数的教学为例,探究情境融合教学模式的应用要点,以数学题目为根本拓展学生思维,并制订更为合理化的教学对策,让学生主动地去发现和解决问题,将学习当作自己的事情.这样才能提高课堂教学效率,才能体现出学生学习的主体地位,实现学习角色的转变.
【关键词】 情境融合;拓展思维;初中数学;锐角三角函数
以前的课堂教学形式是固化的,教师在台上不停地讲,学生实际的学习效率很低.在这样的课堂中,教师永远是课堂的主导者,学生是被动者.在课堂中,学生的思绪并没有完全融入课堂,对于所学内容的理解不透彻,长时间停留在简单模仿的阶段,当遇到一些应用问题时,他们就会措手不及,不知道如何去解决,思维发展受到限制,甚至会和构建主义学习理论相背弃.所以,教师需要在该种状况下及时推行情境融合的教学方式,让学生主动去思考和学习,给学生创建教学情境,并使用小组合作等教学方式让学生在学习中学会合作,懂得如何思考,提高数学应用能力.
一、创设教学情境,激活思维意识
在创设数学情境的过程中,教师需要遵守各项教学原则.首先,需要遵守科学性原则.情境创设的材料和内容都有有理有据,符合学生的认知规律,教师不可为了达到其所设定的教学目标,盲目地去设置一些较为浮夸且真实性较差的情境,所设置的问题要具有让学生充分思考的价值,万不可将情境创设当作万金油,胡乱地进行涂抹式教学.其次,要对学生产生启发.教师所创建的情境活动应源自学生的现实生活,具有较强的启发性,让学生的认知结构处于不平衡的状态,从而产生较为强烈的求知欲望,主动对其认知结构进行修整及补充,让其达到平衡的状态.再次,需要遵守结构性原则.在创设问题情境时,老师需要让情境能够更好地揭示知识的内在逻辑结构.最后,要遵守探究性原则.教师所创设的情境要选择能够激发学生探究欲望的材料及活动形式,控制好探究的程度,不可让其大于学生的学习能力,要能让学生兴奋起来,能动性得到最大释放,使数学思维得到发展.
例如,在进行锐角三角函数的概念教学时,老师可向学生提出问题1:“梯子是我们日常生活中常见的物体,如图1所示,哪个梯子更陡峭?你又是怎样判断出来的呢?”之后将生活问题数学化,向学生提出相似的数学问题2:“如图2所示,梯子AB,EF哪个更陡峭?你是怎样判断的?”通过设置这样的探究性问题,让学生主动去思考,将自己的想法说出来.
在回答完问题1,2之后,教师继续提出问题3:“如图3所示,梯子AB,EF哪个更陡峭?并思考:若倾斜角相同,梯子的垂直高度及水平宽度的比值之间存在何种关系呢?”该教学情境的创设和学生的实际生活相关联,使学生将思考问题的角度转向了生活,刺激了他们大脑的活动.在解决问题1和问题2的过程中,学生会自己思考很多东西,努力将问题拉向自己的生活经验,观察这两个梯子的倾斜程度,而问题3使用控制变量的形式,让学生掌握并了解到倾斜角和边之间的比例关系.这样的教学情境能使学生很容易就掌握了本堂课的知识,课堂学习效率显著提高.
二、小组合作教学,拓展思维宽度
数学是一门抽象的课程,单凭一个人的力量很难进行深入的探究,而在课堂上进行小组合作学习,可以提高学生的学习积极性,让他们主动与其他同学进行合作,提高自己的数学素养,并具备一定的集体主义精神.首先,教师要科学合理地设置小组,对学生的学习能力先进行一个测评,可以是试卷也可以是平时的观察,然而按照一定的原则划分学习小组,组员人数不可超过6人.其次,教师要给每个小组设置合理的任务,每个成员都要有任務,还要在完成分组任务之后合理发挥成员的能动性,让每个人都提出问题,然后大家一块讨论.教师结合学生的综合能力,给其设定相应的学习任务,比如,A同学负责将生活问题转化成数学问题,B同学负责将转化后的数学问题画好示意图,并标好相关条件,C同学根据示意图进行分析讲解,D同学将分析过程写成解题过程.在此过程中,A,B,C,D四个学生随时都可以做出补充和点评,让每个学生都可以参与到数学活动当中.最后,教师需要强化学法及学习习惯的指导,让学生通过小组合作更好地提高自身的团队合作意识.比如,在讲解到锐角三角函数概念时,教师可以直接提出问题:“同学们,你们看图后认为梯子的倾斜角和梯子垂直高度与水平距离的比值有何种联系?”然后给学生5分钟左右的时间让他们充分思考,用所学数学知识进行验证,同时对其内容进行类比及联想,猜测、验证未知的结论.由梯子创设的特殊情境可以让学生概括出一般的结论,而交流合作可以使学生共同发展,拓展思维.
三、问题驱动,拓展思维深度
问题驱动可以让学生始终处在思考的环境之下,大脑思维运转也较快.其和传统的教学方式会有所不同,该种教学方式需要与情境相融合,让学生置身于教师所创设的问题当中,在分析和解决问题时更为深度地理解该模块的知识.在设计问题的过程中,教师要根据班级学生的整体水平及课程目标设置问题,难易结合,突出应用性,并站在引导者的角度聆听学生的想法.教师在将问题驱动融入初中数学锐角三角函数教学时,应让概念的生成更加合理,动态化地生成数学知识概念,让学生去分析和解决问题,将疑惑不解的知识点逐个突破,在课堂上解决所有问题,使学生学习该知识的主动性变得更强,培养学生的数学思维能力.
比如在问题1,2中询问学生哪个梯子更加陡峭,学生通过观察就可以判断梯子的倾斜程度,但是问题3需要通过数学知识的验证才能精准判断,这就使学生出现了不解,促使他们进行数学思考去解决问题,激发了他们的探究欲望.从图1的生活问题到图2的数学问题,从图1,2的垂直高度相同到图3的垂直高度和水平距离都不同,从学生凭借生活经验就能判断到需要利用数学知识才能判断,这种循序渐进下的问题设置,让学生学会用垂直高度和水平宽度的比值去判断梯子的陡峭程度.根据前三个问题的引导,教师还可以向学生抛出问题4:“如图4,小明想通过测量B1C1及AC1算出它们的比来说明梯子AB1的倾斜程度,而小亮则认为,通过测量B2C2及AC2并算出它们的比,也能说明梯子AB1的倾斜程度,你同意谁的看法呢?”
学生可以结合自己之前的经验去解决问题4.问题4还可以变式为问题5:如图5所示,某市一艘海监船某天在岛屿P点周围的海域从南至北依照顺序巡航,在某一时刻航行到了A点位置,此时测量得出该岛屿P处于北偏东30°方向,海监船以每小时20海里的速度继续行驶,在2小时之后行驶到了B点,此时测量岛屿P处于北偏东75°方向,求解此时海监船和岛屿之间的距离BP的长度.
通过变式,学生产生了解题的欲望,并从多立场、多方式去分析、解决问题,突破教学的重难点,感受图形间的变化联系.这种递进升级式的问题设置能有效促进学生的思考及探索,让学生在思考及探索的过程中生成数学概念,完成锐角三角函数的构建任务.在锐角三角函数知识点的教学过程中,教师以创设问题情境、提出问题、解决问题、归纳应用问题、变式问题等一系列方式,不断地驱动学生,加深了学生对锐角三角函数知识的理解.
四、多样化练习,拓展思维广度
初中数学教材中的锐角三角函数知识点是高中学生学习任意角三角函数的基石,所以,在初中数学课堂教学中开展锐角三角函数教学活动,能使学生更好地了解锐角与边之间的关系,让锐角和边得到转化.借助该模块的教学,还会让学生更为深度地理解并感悟数形结合等一系列数学思想.初中数学锐角三角函数涉及实际情境的面很广,想要让学生更为全面且透彻地理解该模块知识,练习方式就必须足够多样化.其练习题的设置不但要能够达到巩固数学知识点的目的,还要能够促进学生思维能力的发展,将重心放到学生最近发展区的问题方面,使得学生的视野变得更加开阔,从而促进学生数学能力的发展,加深学生的思维深度.情境融合和拓展思维模式下的多样化练习主要以学生为课堂的主体,利用练习的方式使得学生学习数学知识的积极性变得更高,同时在这种模式中拓展自身的学习思路,促进创造能力的发展.如设计多样化的基础题型:
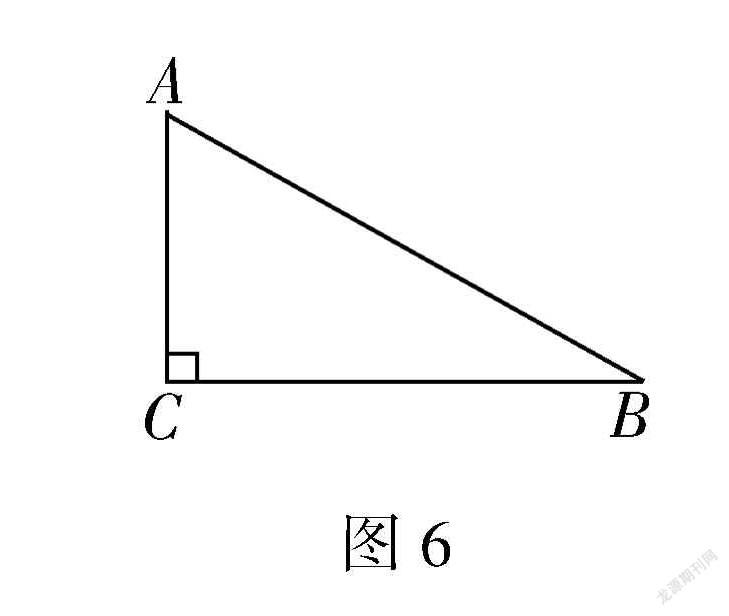
练习1(纯粹的锐角三角函数基础题)如图6所示,Rt△ABC中,∠C=90°,AC=1,AB=2.求sin A,cos B,cos A,sin B,tan A,tan B的值.
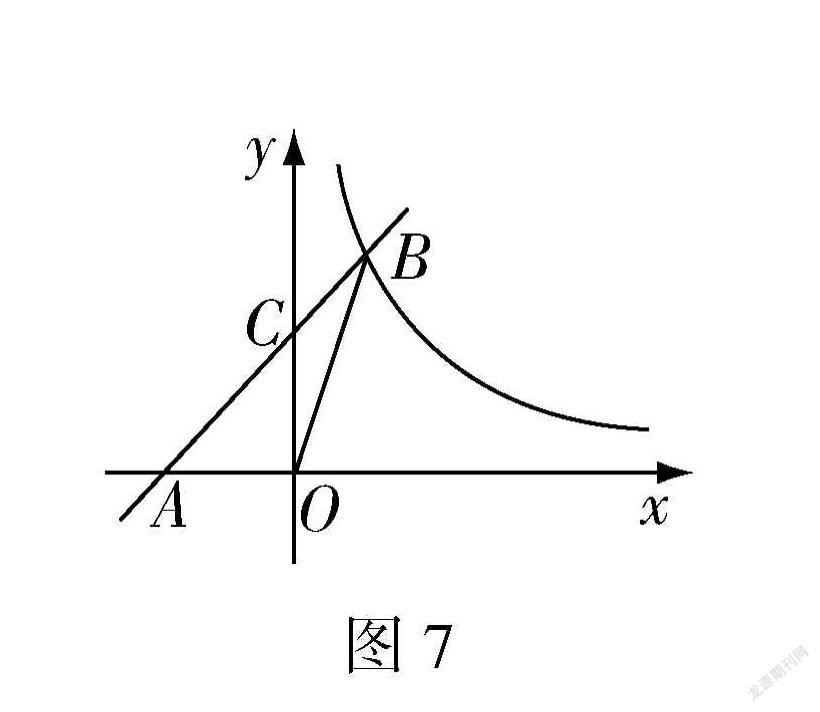
练习2(在直角坐标系中的锐角三角函数)如图7所示,在平面直角坐标系中,直线y=k1x+2与x轴交于点A,与y轴交于点C,与反比例函数y= k2 /x 在第一象限内的图像交于点B,连接BO.若S△OBC=1,tan∠BOC=1 /3 ,求k2的值.
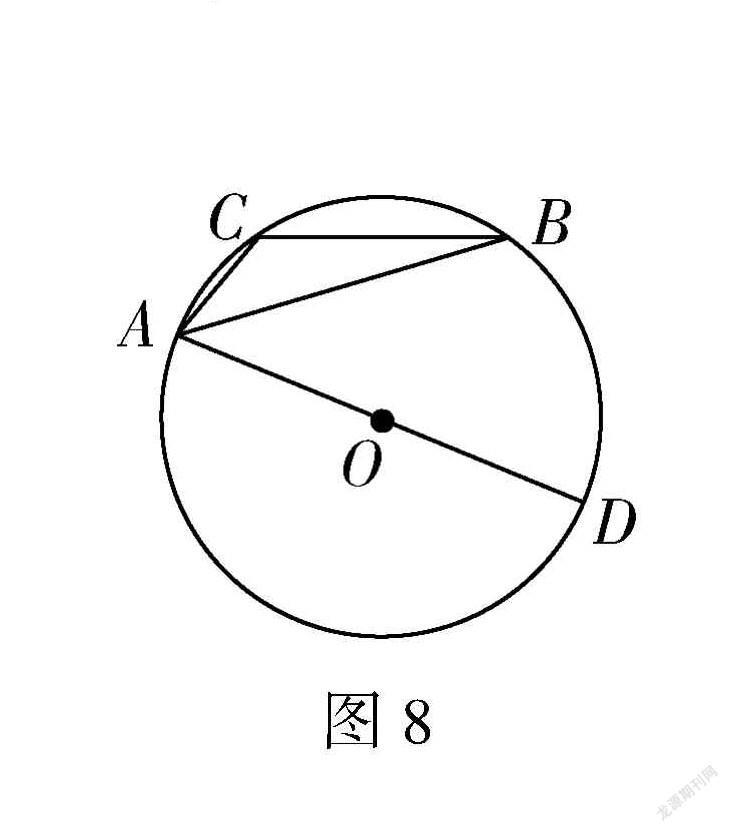
练习3(在圆背景下的锐角三角函数题)如图8所示,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径是4,sin B= 1/4 ,求线段AC的长.
练习4(在动点最值问题中的锐角三角函数题)如图9所示,∠AOB的边OB与x轴的正半轴重合,P是OA上一动点,N(3,0)是OB上一定点,M是ON的中点,∠AOB=30°,要使PM+PN的值最小,求点P的坐标.
练习5(在实际情境中的锐角三角函数题)如图10所示,在某次地震救援中,已探测出某建筑物废墟下方点C处有生命迹象,在废墟一侧地面上选两探测点A,B,AB相距2.1米,探测线与地面的夹角分别是30°和45°,试确定生命所在点C与探测面的距离.
通过练习1,学生对本节课的内容将会掌握得更加充分,同时在思考和质疑的过程中,学生也能间接学习一些锐角三角函数的性质,使学习更加深入.通过练习2和练习3,学生会用新学知识解决问题,在不同背景下深化理解.通过练习4和练习5,学生能学会迁移知识,明确不同情境下同一知识点的运用情况,透过现象看本质.
教师要让学生自主解决问题,不可过多地干预,让学生在独立和合作解决问题中形成较强的数学逻辑思维,突破困难点,更好地领悟本堂课所学知识.
五、结语
在讲解初中数学锐角三角函数知识时,教师需要培养并提高学生的建模意识,合理使用情境融合的教学方式,依据学生的实际生活,多开发建模项目,培养学生灵活运用多种方法解决问题的能力,做到集思广益,锻炼自己的数学思维.多元化地开展练习活动,同时强化构建锐角三角函数应用模型的力度,合理设置教学问题,利用问题引导学生,能够提高学生的数学学习能力.
【参考文献】
[1]梁杏华.三角函数的知识重构[D].华中师范大学,2017.
[2]叶雪琼.问题驱动视野下的锐角三角函数课堂教学研究[D].广州大学,2016.
[3]孫海霞.基于问题学习的初中数学情境教学模式探究[D].西南大学,2011.
