GeoGebra在初中数学教学中的应用

雷勇

摘要：网络的普及改变了人们的生活、工作和学习方式，“互联网+教育”以及人工智能技术对教育教学产生了更大影响，刷新了教师的教学理念和教学方式，改变了学生的学习观念和思维方式。就初中数学学科来讲，其逻辑性、抽象性、严谨性等特点决定了其教学方式与其他学科的差异。结合学科特点选择合适的教学软件，可以大大提高教学效率，有效培养学生的数学素养，发展学生的数学思维。

关键词：初中数学  教学软件  学科素养

数学学科的逻辑性、抽象性、严谨性等特点决定了其教学方式与其他学科的差异。调查发现，在教学中使用PPT的教师人数占99%，这表明初中教师使用计算机教学并没有从学科特点考虑，也是诸如CAI、几何画板、超级几何画板、GeoGebra、Mathmatica等软件在常规课里使用“低频”的原因之一。本文基于自己的实际教学经验，谈谈动态几何教学软件GeoGebra在初中数学教学中的运用。

一、GeoGebra简介

GeoGebra是一款结合了“几何”“代数”与“微积分”的动态数学软件，由美国佛罗里达州亚特兰大学数学教授Markus Hohenwarter所设计。一方面，GeoGebra是一个动态的几何软件，可以在上面画点、向量、线段、直线、多边形、圆锥曲线甚至是函数，事后还可以改变它们的属性。另一方面，也可以直接输入方程和点坐标。所以，GeoGebra也有处理变数的功能，这些变数可以是数字、角度、向量或点坐标;也可以对函数作微分与积分，找出方程的根或计算函数的极大极小值。GeoGebra是一款为小学到大学的数学教学而设计的开源（open source）动态数学软件，类似几何画板，完全免费，是跨平台的数学建模软件，目前支持67国语言，支持Windows、Mac、Android和IOC（iPad）等多种系统，在美国和欧洲获得多项教育类软件奖项，运用此软件可以建立数学模型，进行数学实验，从而为“试验-猜想-证明-应用”的科学探索提供有效的建模工具。它的功能非常强大，其在统计方面的应用和异常强大的中文命令是几何画板所不具备的，无损网页输出和高清图片输出也超越了几何画板。

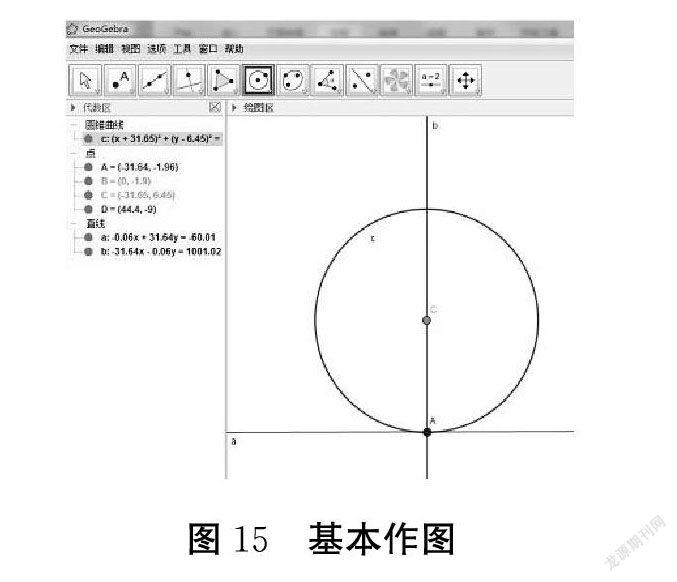
二、GeoGebra基本操作界面

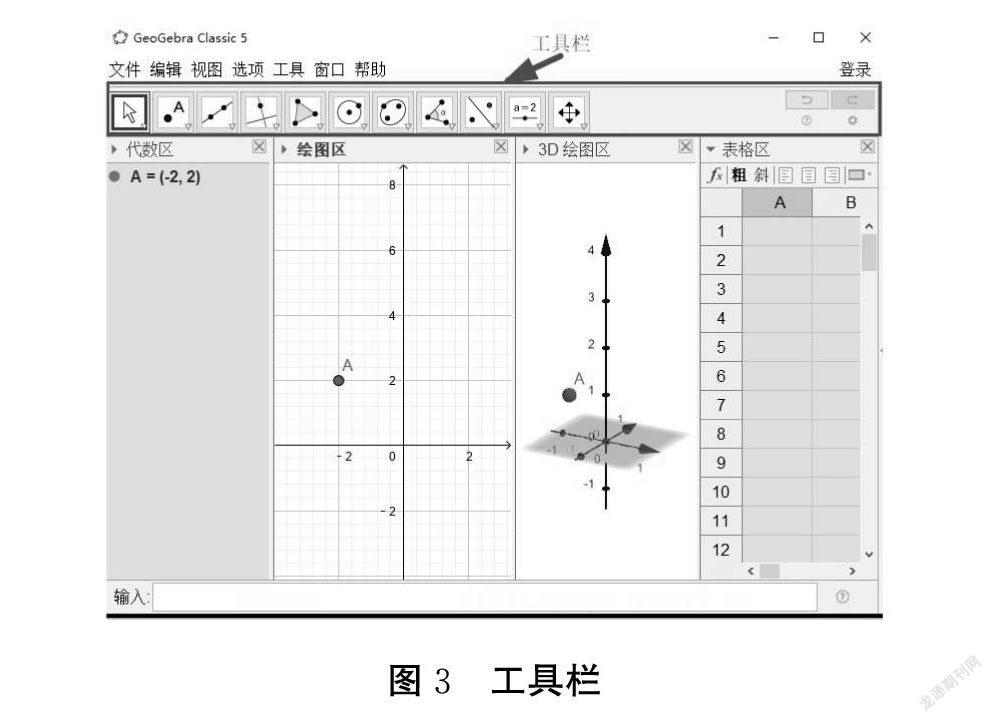
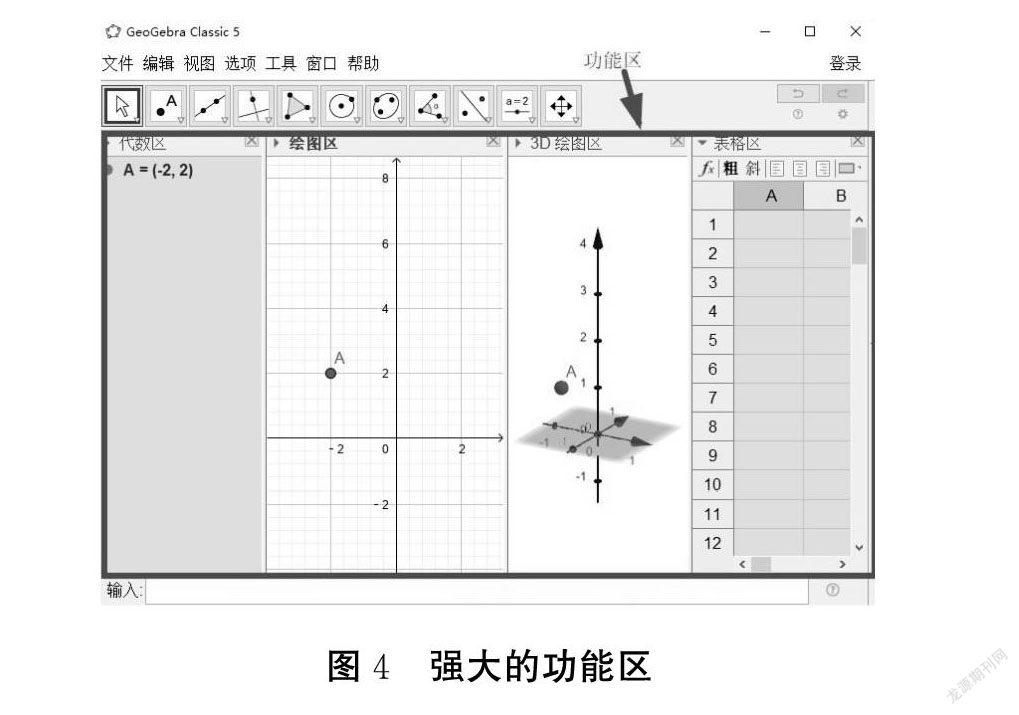
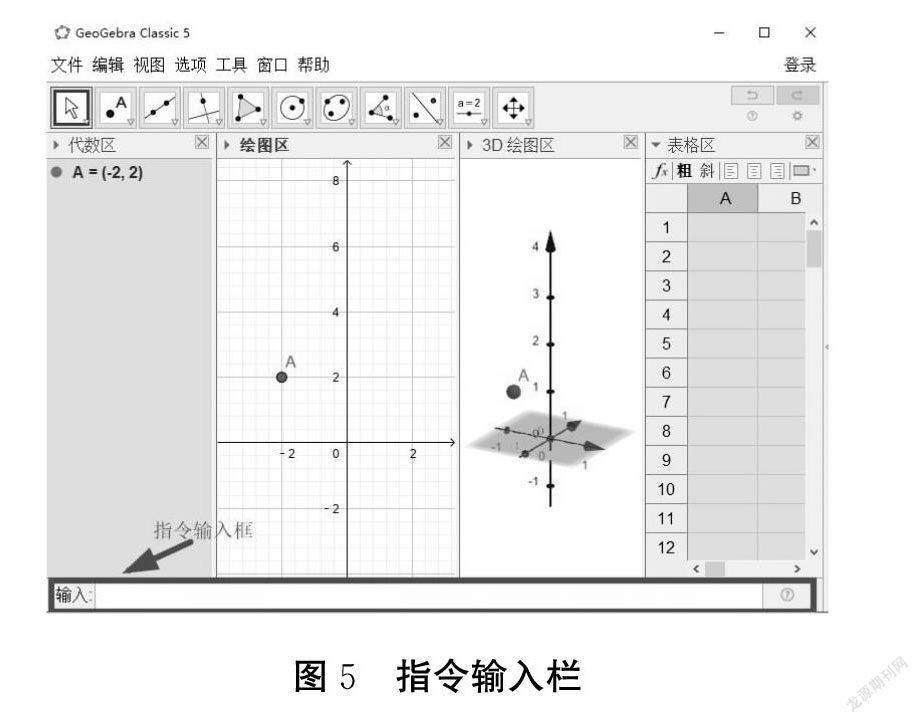
GeoGebra的操作使用很多地方与几何画板有相似之处，该软件工作界面可以分为菜单栏、工具栏、功能区、指令输入框等，如图：

（1）菜单栏与其他软件界面样式相同，增强了软件的熟悉感。

（2）GeoGebra的工具栏与几何画板的有很多相似之处，但更为直观，一些常规的几何图形操作，可以一目了然地从工具栏选择相应的工具进行。

（3）GeoGebra的功能区最能体现该软件强大的教与学性能，展示了数学对象的代数属性和图像属性（2D，3D），还可以与表格等关联使用。

（4）GeoGebra与几何画板的最大区别于之处在于其指令的操作使用突出了数学学科的语言特点，更体现了数学学科与计算机语言的关联性，通过指令操作数学对象可以让數学思维“看得见”。

三、GeoGebra在初中数学教学中的应用

（1）利用GeoGebra设计随机点名系统，在需要向学生提问时，通过该系统能有效克服教师对学生的一些错误认识，同时也使学生对教师的提问不带“感情”色彩而乐于准备和回答。这个点名系统利用GeoGebra做很简单（用Word文档做也可以），只要把班级学生名单直接复制导入新建列表，再做一个按钮——脚本为“更新作图”，如果加上统计功能设计就更好了。

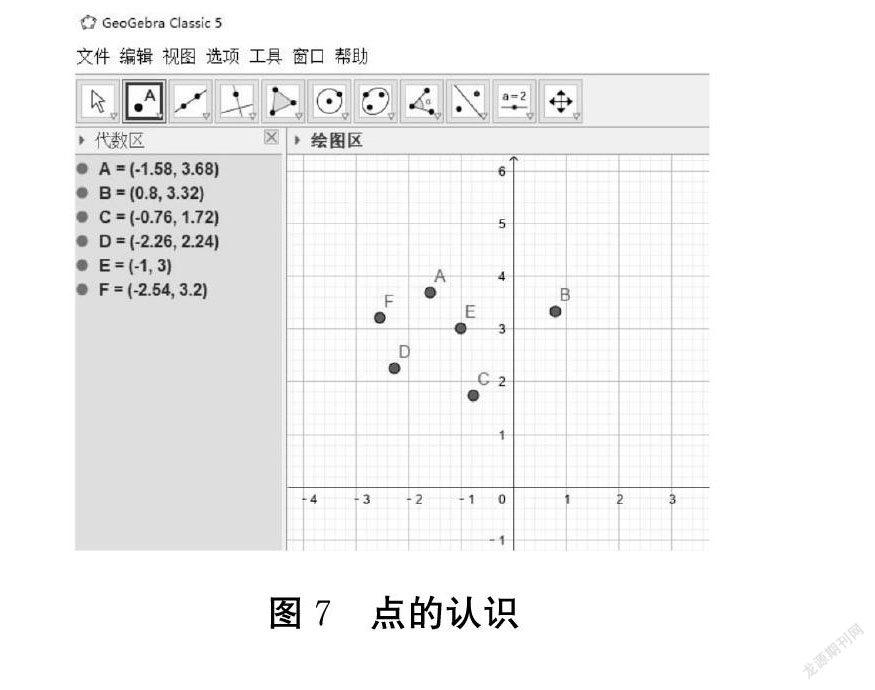
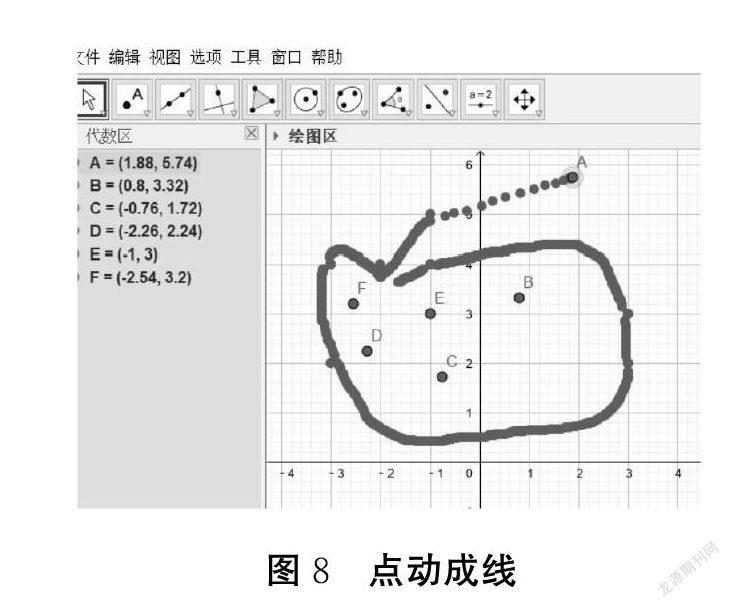
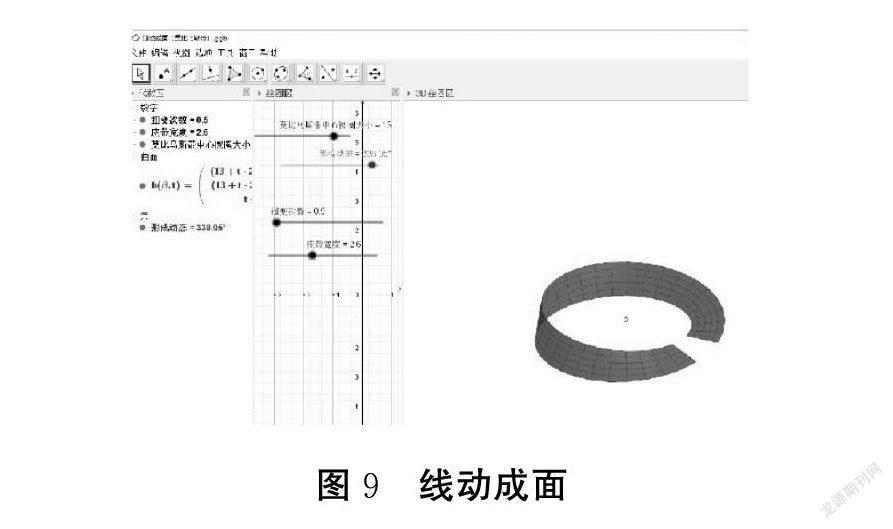
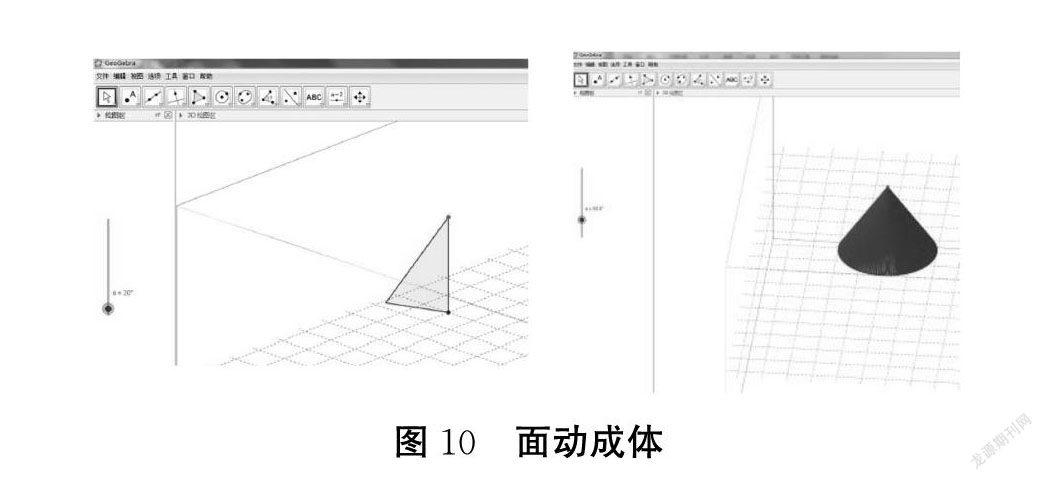
（2）七年级数学上册中的“几何图形的认识”，使用GeoGebra演示，可以利用软件的动态支持、互动性的特点让学生更直观地感知几何图形的点、线、面、体及其彼此间的关系，有利于学生构建几何图形的知识经验，还可以通过改变点的点径样式让学生抽象出点的相关概念。

通过观察“点动成线”的动态演示，学生知道线是由无数个点组成的。在演示中还可以预先设计曲线中的点。维特罗克提出的学习生成模型指出：学习过程不是从感觉经验本身开始，而是从感觉经验的选择性注意开始的。教学设计中，应关注学生的“选择性注意”的认知心理，避免产生杂乱现象干扰重要信息。例如，控制平面图形的旋转，得到相应的“体”。演示过程中要充分运用视觉的敏感性，研究刺激的特征，如：性质、数量、空间分布、与主体的关系等，这些是影响选择性注意的主要因素。就刺激的物理特征而言，有差异的刺激，如形状、大小、强度、颜色、位置等，能够唤醒学生的选择性注意。这一点充分体现出GeoGebra在数学教与学中优于PPT的特点。

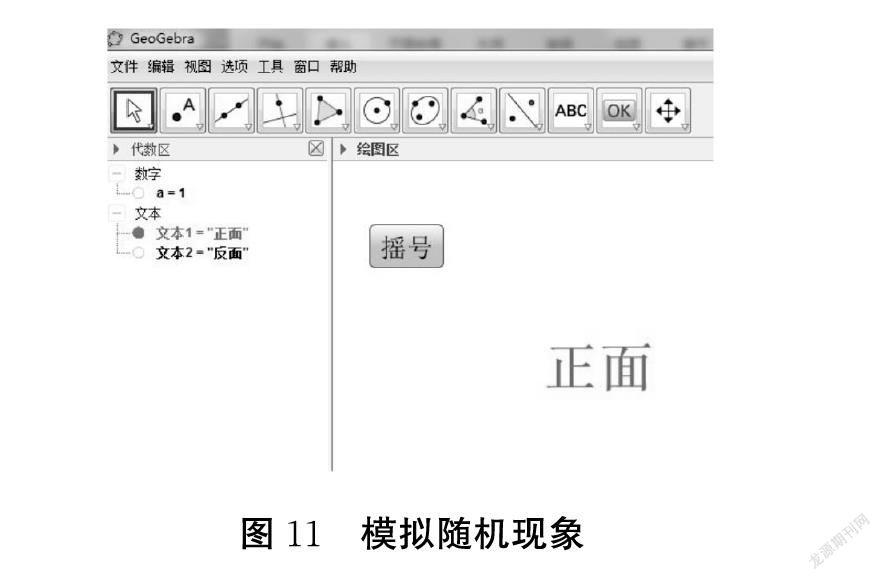
（3）利用GeoGebra来帮助学生理解统计里“随机事件”的“随机”“频率”“概率”含义。

抛掷一枚硬币的模拟实验设计：

说明：通过摇号来统计正面和反面出现的频率来估计概率，让学生知道频率与概率的联系和区别。如要做到硬币的逼真，只要将硬币的正面和反面的图片输入即可。

人机互动的过程实际是一个反馈过程，学习者可以根据自己的意图来操作实验，运用计算机“随机函数”模拟真实随机性，可以更有效地完成实验，操作简便，易于观察，从而有利于得出结论。

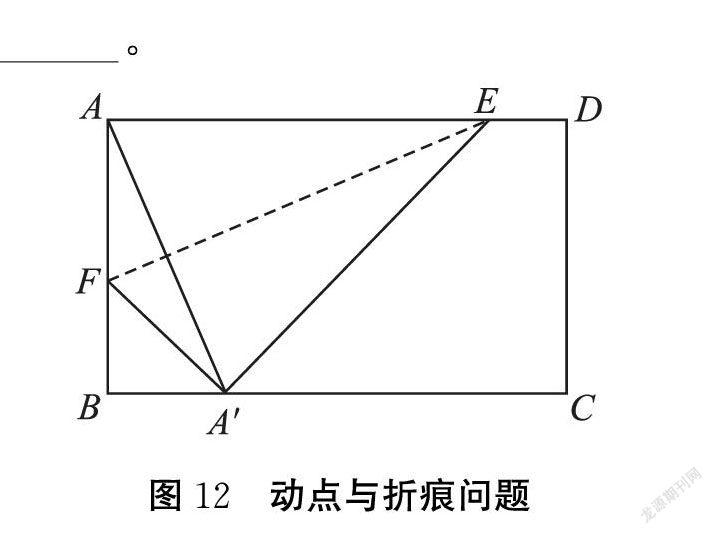
（4）动点问题、折痕问题等试题的探究。

例如，在矩形ABCD中，AB=6，BC=10，把点A通过折叠到边BC上，折痕为EF，则EF最大值为     。

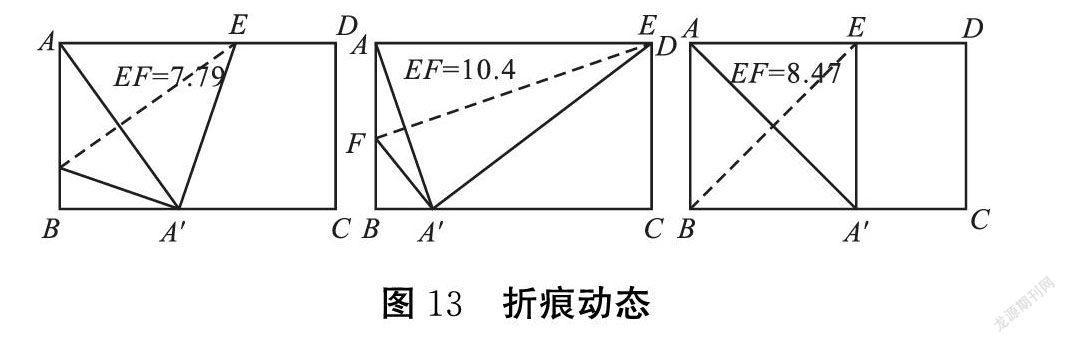
解决这题需要学生通过猜想、归纳、试算、比较等方法，而通过GeoGebra则能更直观地验证学生的猜想。为此我利用GeoGebra进行了相关动态演示，如图13：

通过上面的演示，学生可以观察到点A在运动过程中相关数据的变化：由大到小，接着又由小变大。学生从而归纳出长度变化规律，进而进行猜想，更有利于解决计算问题，培养了用辩证、联系的观点看问题的意识，提高思辨力。

计算方法如下：

由题意可知，当E点与D点重合时，EF的值最大，

设AF=A′F=x，BF=6-x

根据勾股定理可得：CA′=8，则BA′=2

所以（6-x）2+22=x2

解得x=103，所以EF=10 103。

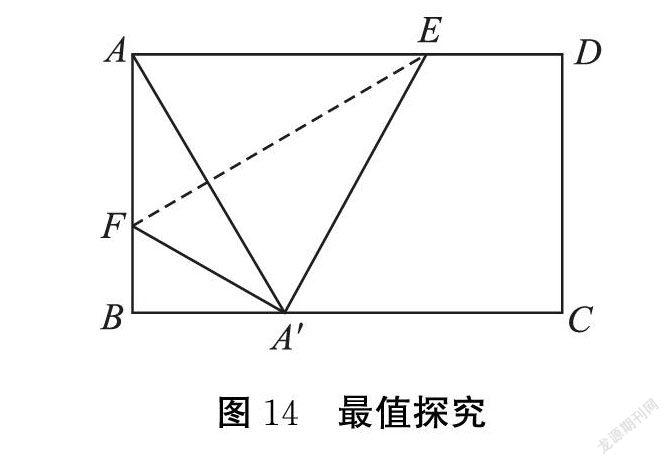
（5）利用GeoGebra来研究动态问题的函数图像刻画

例如上题，可以把AE的值作为一个点的横坐标，以EF的值作为该点的纵坐标，利用追踪就可以知道EF变化情况，如下图（注：红色为EF随AF变化的函数图，这明显不是二次函数图像）：

我们甚至还可以由函数变化图知道此问题中EF还有一个最小值，在时间充足的情况下可以让学生研究怎样求出最小值。

（6）按照范希尔的思维水平制定教学模式：信息——定向引导——显性化——自由探索——整合，通过小组合作交流，然后小组代表操作。在操作之前学生应掌握基本的软件操作知识，避免受“非思维水平因素”影响操作。学生操作可能出现不同结果，让学生自己利用GeoGebra作图，在做中学到几何知识。

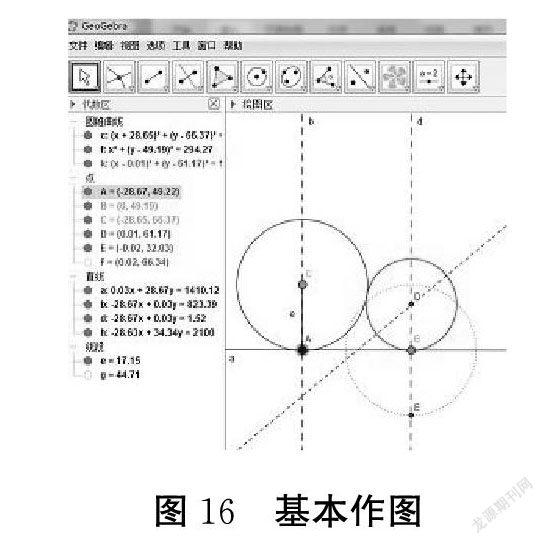
例如：作一个圆与一条已知直线相切。（如图13）

作两个圆与这条直线相切，并且这两个圆也相切。（如图14）

（7）利用GeoGebra设计出随机出题情景，增强课堂效率。

例如：有理数加法运算随机出题。（ 如图15）

四、反思及展望

（1）上课之前要做好准备，注意人机互动，预设好必要的操作流程。

（2）要综合考虑课型、环境、学生的情况，提高使用效果。

（3）要与PPT或flash等软件结合使用，增强实效。

（4）要与同事合作交流、资源共享，共同提高教学水平。

（5）要认识到任何工具、技术的作用都只是辅助教学。

无论从新的教育教学理念还是新的教育教学技术手段来说，农村学校都相对落后，这也就是说农村学校将在利用相关工具上有更大的作为。智慧教学，任重道远。

参考文献：

[1]M.W.艾森克，M.T.基恩.认知心理学（第5版）[M].张明，等，译.上海：华东师范大学出版社，2020.

[2]萬维钢（同人于野）.万万没想到：用理工科思维理解世界[M].北京：电子工业出版社，2015.

[3]吴华，何晓頔.范希尔理论下动态几何技术应用于祖暅原理的教学研究[J].辽宁教育，2013.

责任编辑：黄大灿